Lesson 2 3 The Laws of Limits Objectives

Lesson 2 -3 The Laws of Limits

Objectives • Find Limits using the Laws of Limits • Understand use the Squeeze Theorem

Vocabulary • Greatest Integer Function – [[ x ]], the largest integer that is less than or equal to x • Continuous – (studied in detail in 2. 5) no interrupt or abrupt change in the function

Laws of Limits Summary lim f(x) Suppose c is a constant and the and lim g(x) x a 1. lim [f(x) + g(x)] = lim f(x) + lim g(x) x a 2. lim [f(x) - g(x)] = x a Difference Law x a Constant Multiple Law x a 4. lim [f(x) • g(x)] = x a x a lim f(x) / lim g(x) , if lim g(x) ≠ 0 x a 6. lim [f(x)]ⁿ = x a [lim f(x)]ⁿ x a Product Law lim f(x) • lim g(x) x a 5. lim [f(x) / g(x)] Quotient Law x a (n is a positive integer) from Product x a 7. lim c = c 8. lim x =a Special Limits x a 9. lim xⁿ = aⁿ 10. ⁿ = √a ⁿ lim √x from 6 and 8 x a x a lim g(x) = c lim f(x) x a ⁿ 11. lim √f(x) Sum Law x a lim f(x) - x a 3. lim [cf(x)] exist. Then --- x a = ⁿ√lim f(x) x a Generalization

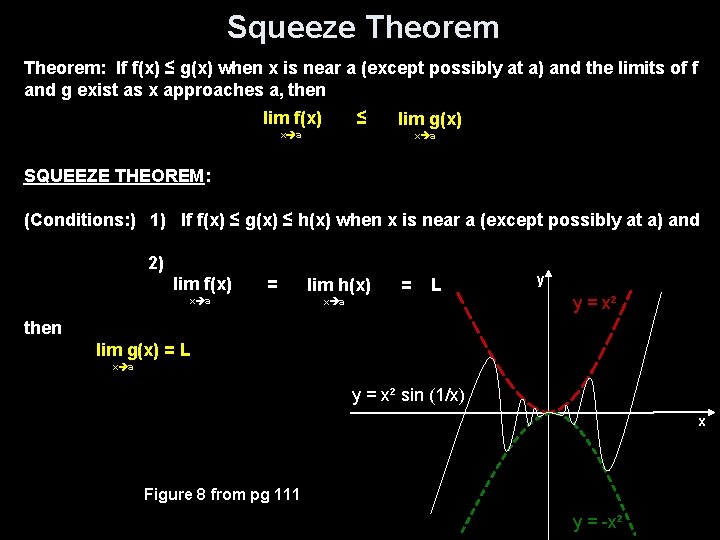
Squeeze Theorem: If f(x) ≤ g(x) when x is near a (except possibly at a) and the limits of f and g exist as x approaches a, then lim f(x) ≤ lim g(x) x a SQUEEZE THEOREM: (Conditions: ) 1) If f(x) ≤ g(x) ≤ h(x) when x is near a (except possibly at a) and 2) lim f(x) = x a lim h(x) = L x a y y = x² then lim g(x) = L x a y = x² sin (1/x) x Figure 8 from pg 111 y = -x²

Example 1 Find Lim 4 x² - 10 x + 3 = 87 x→ 6 Polynomials – just use Direct Substitution – f(a)

Example 2 Find x² - 6 x + 5 Lim ---------x– 1 x→ 1 = -4 If direct substitution fails (yields 0/0) try factoring To algebraically simplify

Example 3 Find Lim x→ 5 3 4 x + 44 ------6 x – 29 = 4 If direct substitution works, then be happy!

Example 4 Find Lim f(x) x→ 3 = DNE where f(x) = x² x≥ 3 6 x – 4 x<3 Since we are at a “break point”, if direct substitution for the one-sided limits yields different values, then the two-sided limit is DNE

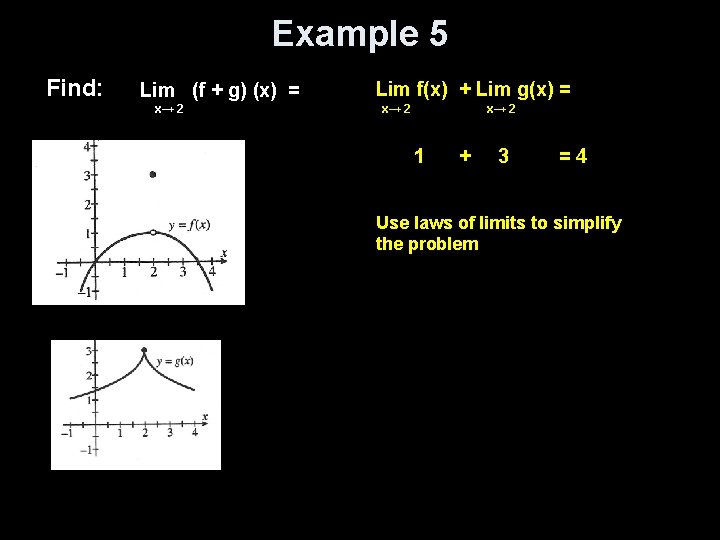
Example 5 Find: Lim (f + g) (x) = x→ 2 Lim f(x) + Lim g(x) = x→ 2 1 + 3 =4 Use laws of limits to simplify the problem

Example 6 Find (1/x) - x Lim -------(1/x) - 1 x→ 1 = 2 If direct substitution yields 0/0, then algebraically simplify the expression.

Example 7 Find 2 + x - x Lim ---------x x→ 0 = DNE If direct substitution yields 0/0, then algebraically simplify the expression. They don’t always exist!

Proof Find sin θ Lim ------ = θ θ→ 1 1 Since area of the inscribed ∆ ≤ area of the sector ≤ outer ∆ ½ sin θ ≤ ½ tan θ so (sin θ) / θ ≤ 1 Next multiply the second part by (2 cos θ) / θ and we get cos θ ≤ (sin θ) / θ Combine and take the limits Lim cos θ ≤ lim (sin θ) / θ ≤ lim 1 1 ≤ lim (sin θ) / θ ≤ 1

Summary & Homework • Summary: – – Try to find the limit via direct substitution Use algebra to simplify into useable form Use laws of limits to simplify and solve Use squeeze theorem • Homework: pg 111 -113: [Day 1] 1, 3, 6, 10, 11, 13, 20 [Day 2] 33, 40, 41, 52