Lesson 2 3 Conditional Statements TARGETS Analyze statements

Content Standards G-CO. 9 Prove theorems about lines and angles. Theorems include: vertical angles

You used data to find patterns and make predictions. • Analyze statements in if-then

2 -3 Vocabulary conditional statement if-then statement hypothesis conclusion related conditionals converse inverse contrapositive

LESSON 2 -3: Conditional Statements Let’s revisit Compound Statements. A. p ^ q :

LESSON 2 -3: Conditional Statements Think about a situation that might be represented by

LESSON 2 -3: Conditional Statements Conditional Statement A compound statement that can be written

LESSON 2 -3: Conditional Statements Conditional Statement has 2 parts: If you are sick,

LESSON 2 -3: Conditional Statements If you are sick, then you have a make

LESSON 2 -3: Conditional Statements EXAMPLE 1 Identify the Hypothesis and Conclusion Identify the

LESSON 2 -3: Conditional Statements Conditional Statement Can be written without using if and

LESSON 2 -3: Conditional Statements EXAMPLE 2 Write a Conditional in If-Then Form Identify

LESSON 2 -3: Conditional Statements Truth Values of Conditional Statement If Tom finishes his

LESSON 2 -3: Conditional Statements EXAMPLE 3 Truth Values of Conditionals Determine the truth

LESSON 2 -3: Conditional Statements Related Conditionals p q If a polygon has 6

LESSON 2 -3: Conditional Statements Logically Equivalent Conditional (p q) & Contrapositive (~q ~p)

LESSON 2 -3: Conditional Statements EXAMPLE 3 Related Conditionals Write the converse, inverse, and

Slides: 24

Download presentation

Lesson 2 -3: Conditional Statements TARGETS • Analyze statements in if-then form. • Write converses, inverses, and contrapositives.

Content Standards G-CO. 9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. Mathematical Practices 2 Reason abstractly and quantitatively. 3 Construct viable arguments and critique the reasoning of others. 6 Attend to precision. 8 Look for and express regularity in repeated reasoning.

You used data to find patterns and make predictions. • Analyze statements in if-then form. • Write converses, inverses, and contrapositives.

2 -3 Vocabulary conditional statement if-then statement hypothesis conclusion related conditionals converse inverse contrapositive logically equivalent

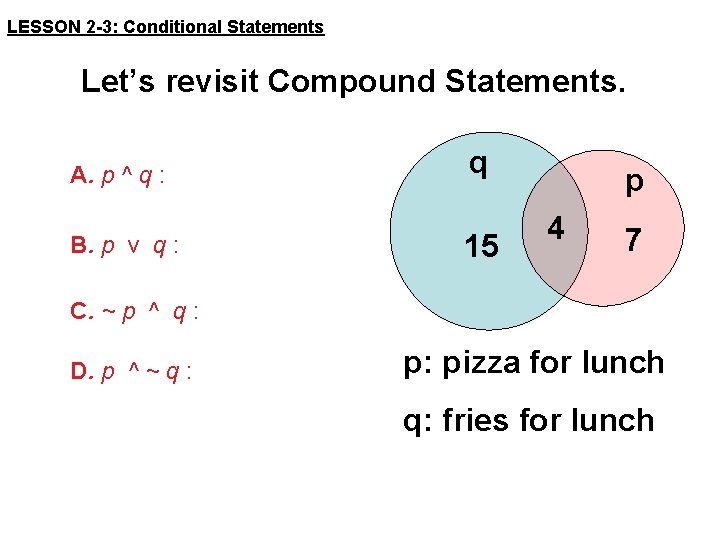
LESSON 2 -3: Conditional Statements Let’s revisit Compound Statements. A. p ^ q : B. p v q : q 15 p 4 7 C. ~ p ^ q : D. p ^ ~ q : p: pizza for lunch q: fries for lunch

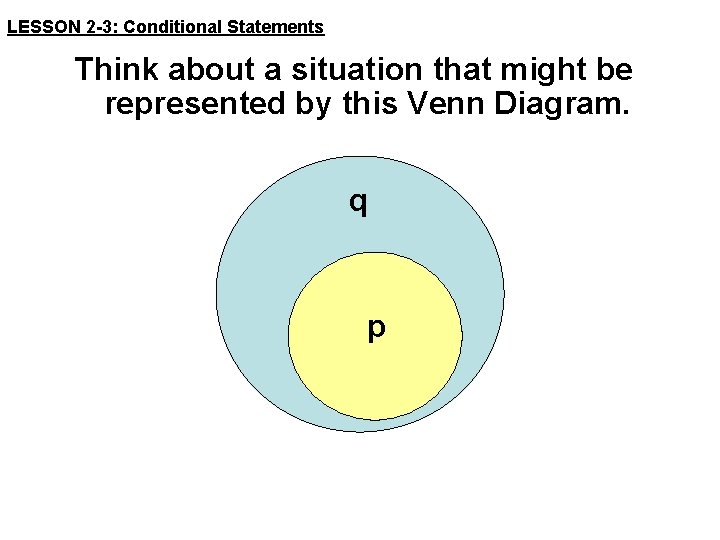
LESSON 2 -3: Conditional Statements Think about a situation that might be represented by this Venn Diagram. q p

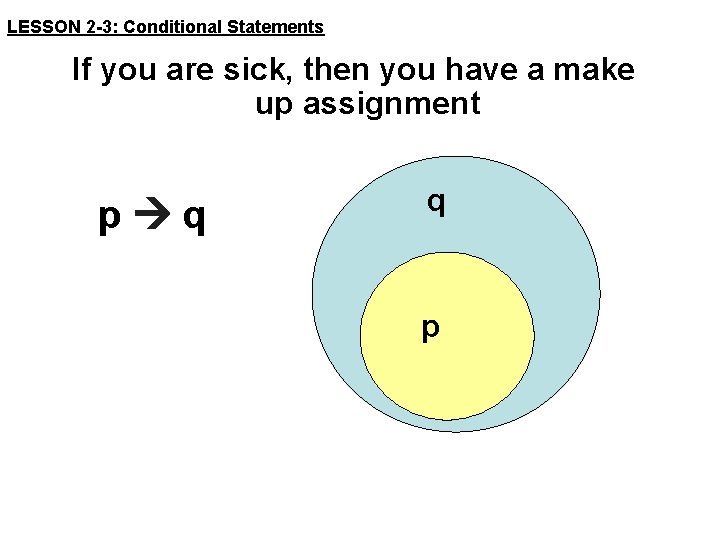
LESSON 2 -3: Conditional Statements Conditional Statement A compound statement that can be written in the form of ‘If…, then…’ p q , read as ‘if p, then q’ p: you are sick q: you have a make up assignment to complete If you are sick, then you have a make up assignment to complete OR If you are sick, you have a make up assignment to complete

LESSON 2 -3: Conditional Statements Conditional Statement has 2 parts: If you are sick, hypothesis then you have a make up assignment to complete conclusion

LESSON 2 -3: Conditional Statements If you are sick, then you have a make up assignment p q q p

LESSON 2 -3: Conditional Statements EXAMPLE 1 Identify the Hypothesis and Conclusion Identify the hypothesis and conclusion of the following statements. A. If a polygon has 6 sides, then it is a hexagon. B. A number is divisible by 10 if its last digit is a 0.

LESSON 2 -3: Conditional Statements EXAMPLE 1 Identify the Hypothesis and Conclusion Identify the hypothesis and conclusion of the following statements. C. If you are a baby, then you will cry. D. Another performance will be scheduled if the first one is sold out.

LESSON 2 -3: Conditional Statements Conditional Statement Can be written without using if and then To write statements in if-then form: 1. ID the Hypothesis 2. ID the Conclusion 3. Rewrite in ‘if…, then…’ form A mammal is a warm-blooded animal

LESSON 2 -3: Conditional Statements EXAMPLE 2 Write a Conditional in If-Then Form Identify the hypothesis and conclusion of the following statement. Then write the statement in the if -then form. A. Measured distance is positive. B. A five-sided polygon is a pentagon.

LESSON 2 -3: Conditional Statements EXAMPLE 2 Write a Conditional in If-Then Form Identify the hypothesis and conclusion of the following statement. Then write the statement in the if -then form. C. Four quarters can be exchanged for a $1 bill. D. The sum of the measures of two supplementary angles is 180.

LESSON 2 -3: Conditional Statements Truth Values of Conditional Statement If Tom finishes his homework, then he will clean his room

LESSON 2 -3: Conditional Statements Truth Values of Conditional Statement If Tom finishes his homework, then he will clean his room Hypothesis (p) Conclusion (q) Conditional (p q) Tom finishes his homework Tom cleans his room If Tom finishes his homework, then he will clean is room • A conditional is false ONLY when its hypothesis is true and conclusion is false • When the hypothesis is false, the conditional will ALWAYS be true

LESSON 2 -3: Conditional Statements EXAMPLE 3 Truth Values of Conditionals Determine the truth value of each conditional statement. If true, explain your reasoning. If false, give a counterexample. A. If you subtract a whole number from another whole number, the result is also a whole number. B. If last month was February, then this month is March.

LESSON 2 -3: Conditional Statements EXAMPLE 3 Truth Values of Conditionals Determine the truth value of each conditional statement. If true, explain your reasoning. If false, give a counterexample. C. When a rectangle has an obtuse angle, it is a parallelogram. D. If yesterday was Tuesday, then today is Monday.

Lesson 2 -3: Conditional Statements TARGETS • Analyze statements in if-then form. • Write converses, inverses, and contrapositives.

LESSON 2 -3: Conditional Statements Related Conditionals p q If a polygon has 6 sides, then it is a hexagon. Converse: q p , hypothesis & conclusion switch If a polygon is a hexagon, then it has 6 sides. Inverse: ~p ~q , negate both hypothesis and conclusion If a polygon does not have 6 sides, then it is not hexagon. Contrapositive: ~q ~p , negate both hypothesis and conclusion of the converse If a polygon is not a hexagon, then it does not have 6 sides.

LESSON 2 -3: Conditional Statements Logically Equivalent Conditional (p q) & Contrapositive (~q ~p) are either both TRUE or both FALSE Converse (q p) & Inverse (~p ~q) are either both TRUE or both FALSE

LESSON 2 -3: Conditional Statements EXAMPLE 3 Related Conditionals Write the converse, inverse, and contrapositive of the following true statement. Determine the truth value of each statement. If a statement is false, give a counterexample. All squares are quadrilaterals. Conditional: Converse: Inverse: Contrapositive:

LESSON 2 -3: Conditional Statements EXAMPLE 3 Related Conditionals Write the converse, inverse, and contrapositive of the following true statement. Determine the truth value of each statement. If a statement is false, give a counterexample. All whole numbers are integers. Conditional: Converse: Inverse: Contrapositive: