Lesson 2 1 Conditional Statements Conditional Statement Two

Lesson 2. 1 Conditional Statements

Conditional Statement Two parts: hypothesis and conclusion If-then form

Ex. If it is noon in Philadelphia, then it is 9 A. M. in Los Angeles.

“if” contains hypothesis “then” contains conclusion

Example 1 Write the statements in if -then form.

1. A number divisible by 9 is also divisible by 3.

If a number is divisible by 9, then it is divisible by 3.

2. All mammals breathe oxygen.

If an animal is a mammal, then it breathes oxygen.

3. Two points are collinear if they lie on the same line.

If two points lie on the same line, then they are collinear.

Conditional Statements can be true or false. If they are false, we must find a counterexample.

Example 2 Determine if the statement is true or false. If it is false, find a counterexample

If a point is distinct, then it may lie on more than one line.

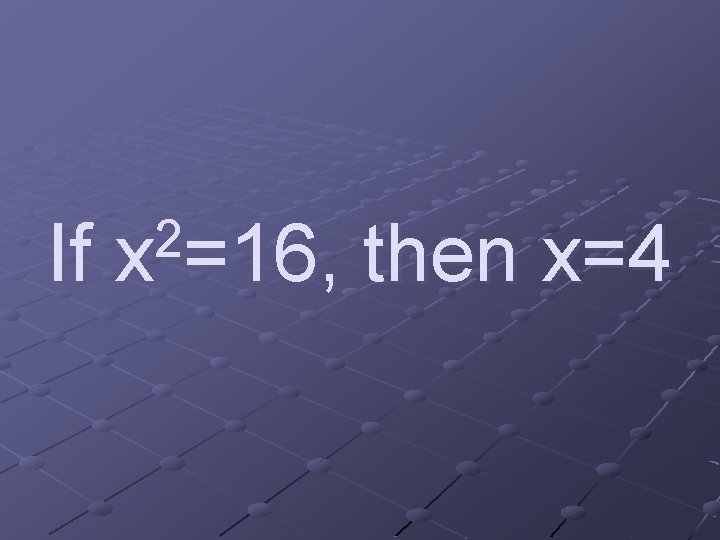
If 2 x =16, then x=4

If a number is odd, then it is divisible by 3.

Converse: formed by switching the hypothesis and conclusion “flip-flop”

Statement: If you see lightning, then you hear thunder? Converse: If you hear thunder, then you see lightning. Are both these true?

If 2 segments are congruent, then they have the same length.

Converse: If two segments have the same length, then they are congruent.

If an angle is acute, then its measure is less than 90 degrees.

Converse: If an angle measures less than 90°, then it is acute.

Inverse: negate the hypothesis and conclusion

Contrapositive: Negate the converse “Negative flip-flop”

If m<A=120° degrees, then the angle is obtuse.

Inverse: If m<A≠ 120° degrees, then the angle is not obtuse.

Converse: If the angle is obtuse, then m<A=120°.

Contrapositive: If the angle is not obtuse, then m<A ≠ 120.

Statement: If m<P=90°, then <P is a right angle.

Inverse: If m<P ≠ 90°, then <P is not a right angle.

Converse: If <P is a right angle, then m<P=90.

Contrapositive: If <P is not a right angle, then m<P ≠ 90.

Statement: If an animal is a fish, then it can swim.

Inverse If an animal is not a fish, then it can not swim.

Converse If an animal can swim, then it is a fish.

Contrapositive If an animal can’t swim, then it is not a fish.

Statement If x=y, then 3 x=3 y.

Inverse If x≠y, then 3 x ≠ 3 y.

Converse If 3 x=3 y, then x=y.

Contrapositive If 3 x ≠ 3 y, then x ≠y.

Equivalent Statements: two statements are both true or both false.

Postulate 5 Through any 2 points, there exists exactly one line.

Postulate 6 A line contains AT LEAST 2 points

Postulate 7 If two lines intersect, then their intersection is exactly one point.

Postulate 8 Through any 3 NONCOLLINEAR points, there exists exactly one plane.

Postulate 9 A plane contains AT LEAST 3 NONCOLLINEAR points.

Postulate 10 If two points lie in a plane, then the line containing them also lies in the plane.

Postulate 11 If two planes intersect, then their intersection is a line.

Write postulate 5 in if-then form. Through any 2 points, there exists exactly one line. If there are 2 points, then there exists exactly one line.

Inverse If there is not two points, then there is not exactly one line.

Converse If there exists exactly one line, then there are 2 points.

Contrapositive If there is not exactly one line, then there is not 2 points.

Postulate 8 Through any 3 noncollinear points, there exists exactly one plane. If there are 3 noncollinear points, then there exists exactly one plane.

Inverse If there are not 3 noncollinear points, then there is not exactly one plane.

Converse If there exists exactly one plane, then there are 3 noncollinear points.

Contrapositive If there is not exactly one plane, then there are not 3 noncollinear points.