Lesson 2 1 Conditional Statements Conditional Statement Defn

Lesson 2 -1 Conditional Statements

Conditional Statement Defn. A conditional statement is a statement that can be written as an ifthen statement. That is, as “If _______, then _______. ”

Example: If your feet smell and your nose runs, then you're built upside down.

Conditional Statements have two parts: The hypothesis is the part of a conditional statement that follows “if” (when written in if-then form. ) It is the given information, or the condition. If a number is prime, then a number has exactly two divisors. Leave off “if” and Hypothesis: a number is prime comma.

Conditional Statements have two parts: The conclusion is the part of a conditional statement that follows “then” (when written in if-then form. ) It is the result of the given information. If a number is prime, then a number has exactly two divisors. Leave off “then” and Conclusion: a number has exactly two divisors period

Rewriting Conditional Statements Conditional statements can be put into an “if-then” form to clarify which part is the hypothesis and which is the conclusion. Method: Turn the subject into a hypothesis.

Example 1: Vertical angles are congruent. can be written as. . . If two angles are vertical, then they are congruent.

Example 2: Seals swim. can be written as. . . If an animal is a seal, then it swims.

Example 3: Babies are illogical. can be written as. . . If a person is a baby, then the person is illogical.

IF …THEN vs. IMPLIES Another way of writing an if-then statement is using the word implies. Two angles are vertical implies they are congruent.

Conditional Statements can be true or false: • A conditional statement is false only when the hypothesis is true, but the conclusion is false. • A counterexample is an example used to show that a statement is not always true and therefore false.

Counterexample Statement: If you live in Virginia, then you live in Richmond, VA. Is there a counterexample? YES. . . Anyone who lives in Virginia, but not Richmond, VA. Therefore ( ) the statement is false.

Symbolic Logic Symbols can be used to modify or connect statements.

Symbols for Hypothesis and Conclusion Lower case letters, such as p and q, are frequently used to represent the hypothesis and conclusion. if p, then q or p implies q

Symbols for Hypothesis and Conclusion Example p: a number is prime q: a number has exactly two divisors if p, then q or p implies q If a number is prime, then it has exactly two divisors.

is used to represent the words “if … then” or “implies”

p q means if p, then q or p implies q

Example p: a number is prime q: a number has exactly two divisors p q: If a number is prime, then it has exactly two divisors.

~ is used to represent the word “not” • ~ p is the negation of p. • The negation of a statement is the denial of the statement. Add or remove the word “not. ” • To negate, write ~ p.

Example p: the angle is obtuse ~p: the angle is not obtuse Be careful because ~p means that the angle could be acute, right, or straight.

Example p: James doesn’t like fish. ~p: James likes fish. Notice: ~p took the “not” out… it would have been a double negative (not not)

is used to represent the word “and”

Example p: a number is even q: a number is divisible by 3 p q: A number is even and it is divisible by 3. 6, 12, 18, 24, 30, 36, 42. . .

is used to represent the word “or”

Example p: a number is even q: a number is divisible by 3 p q: A number is even or it is divisible by 3. 2, 3, 4, 6, 8, 9, 10, 12, 14, 15, . . .

is used to represent the word “therefore”

Example Therefore, the statement is false

Different Forms of Conditional Statements

Forms of Conditional Statements Converse: Statement formed from a conditional statement by switching the hypothesis and conclusion (q p) p q If two angles are vertical, then they are congruent. q p If two angles are congruent, then they are vertical. Are these statements true or false? Continued…. .

Forms of Conditional Statements Inverse: Statement formed from a conditional statement by negating both the hypothesis and conclusion. (~p ~q) p q : If two angles are vertical, then they are congruent. ~p ~q: If two angles are not vertical, then they are not congruent. Are these statements true or false?

Forms of Conditional Statements Contrapositive: Statement formed from a conditional statement by switching and negating both the hypothesis and conclusion. (~q ~p) p q : If two angles are vertical, then they are congruent. ~q ~p: If they are not congruent, then two angles are not vertical Are these statements true or false?

Contrapositives are logically equivalent to the original conditional statement. • If p q is true, then q p is true. • If p q is false, then q p is false.

Biconditional • When a conditional statement and its converse are both true, the two statements may be combined. • A statement combining a conditional statement and its converse is a biconditional. • Use the phrase if and only if which is abbreviated iff • Use the symbol

Definitions are always biconditional l Statement: p q l If an angle is right then it measures 90. l Converse: q p l If an angle measures 90 , then it is right. l Biconditional: p q l An angle is right iff it measures 90.

Biconditional • A biconditional is in the form: Hypothesis if and only if Conclusion. or Hypothesis iff Conclusion or Hypothesis Conclusion

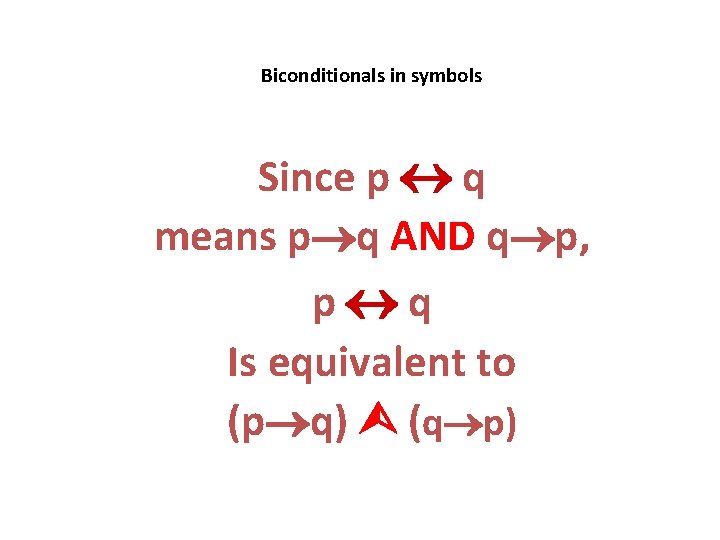
Biconditionals in symbols Since p q means p q AND q p, p q Is equivalent to (p q) (q p)