Lesson 19 AC Source Transformation and Nodal Analysis

Lesson 19: AC Source Transformation and Nodal Analysis 1

Learning Objectives • Construct equivalent circuits by converting an AC voltage source and a resistor to an AC current source and a resistor. • Apply Nodal Analysis to an AC Circuit. 2

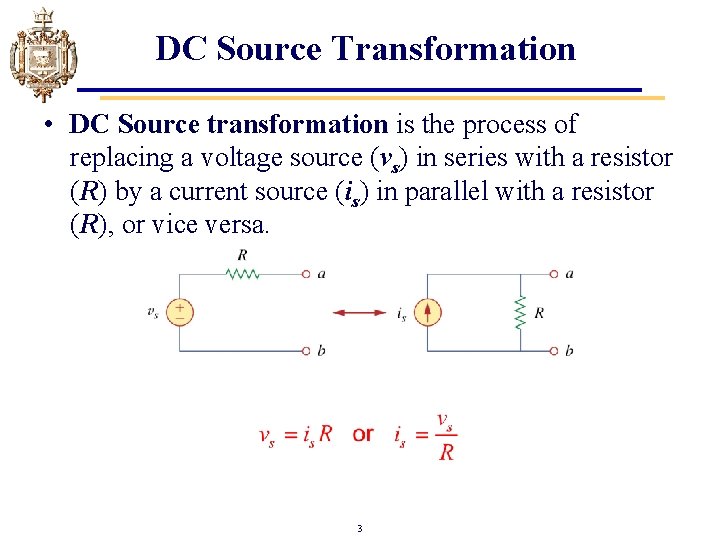
DC Source Transformation • DC Source transformation is the process of replacing a voltage source (vs) in series with a resistor (R) by a current source (is) in parallel with a resistor (R), or vice versa. 3

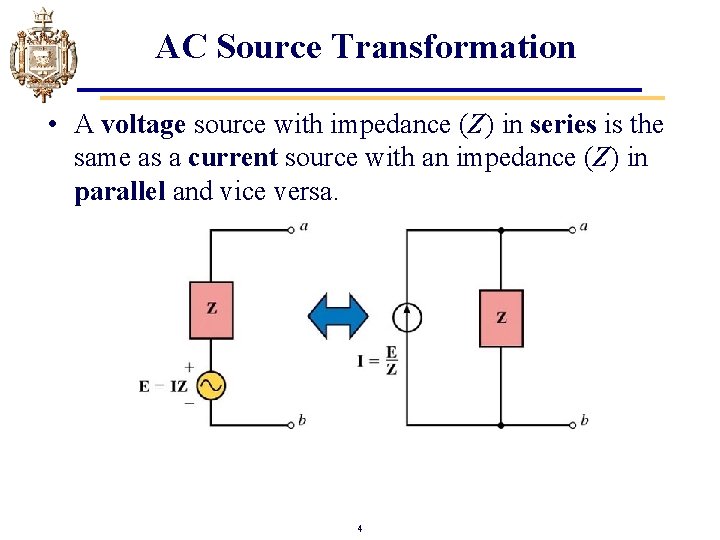
AC Source Transformation • A voltage source with impedance (Z) in series is the same as a current source with an impedance (Z) in parallel and vice versa. 4

Example Problem 1 Convert the voltage source to a current source: Use the same rules as you would with a DC source conversion only this time you are calculating your source conversion with complex numbers and ‘moving’ the impedance. 9Ω 40Ω 5

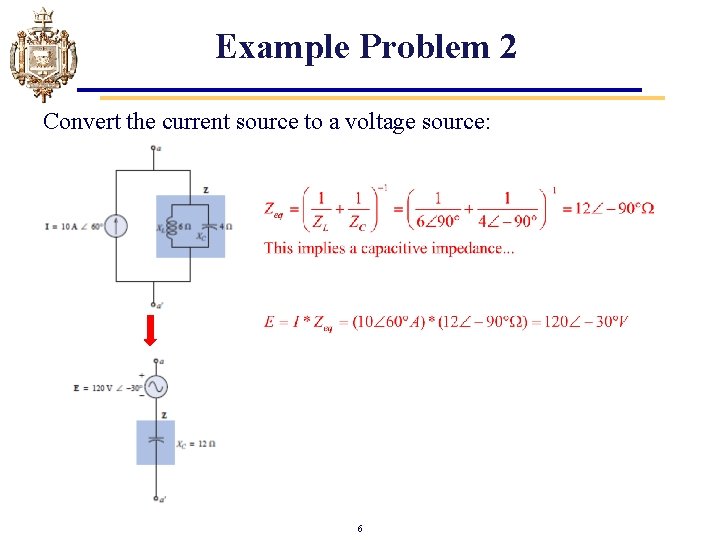
Example Problem 2 Convert the current source to a voltage source: 6

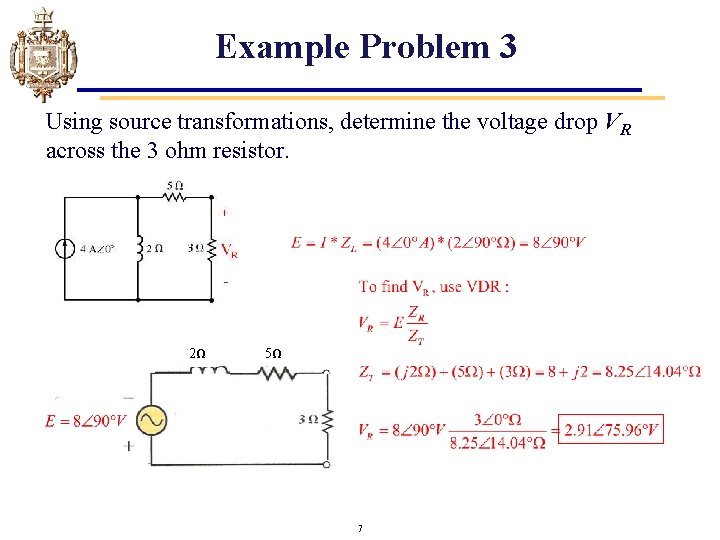
Example Problem 3 Using source transformations, determine the voltage drop VR across the 3 ohm resistor. 2Ω 5Ω 7

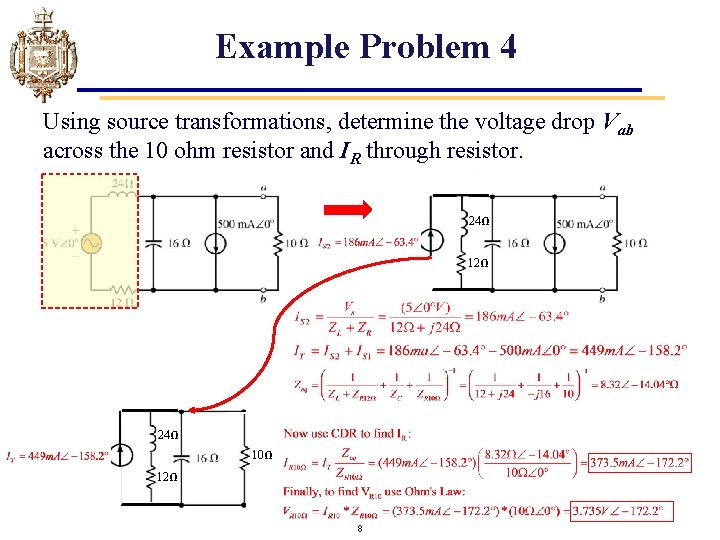
Example Problem 4 Using source transformations, determine the voltage drop Vab across the 10 ohm resistor and IR through resistor. 24Ω 12Ω 24Ω 10Ω 12Ω 8

AC Nodal Analysis General Approach (similar to the DC approach): • The fundamental steps are the following: 1. Determine the number of nodes within the network. 2. Pick a reference node and label each remaining node with a subscripted value of voltage: Va, Vb, and so on. 3. Apply Kirchhoff’s current law at each node except the reference. • Assume that all unknown currents leave the node for each application of Kirchhoff’s current law. 4. Solve the resulting equations for the nodal voltages. 9

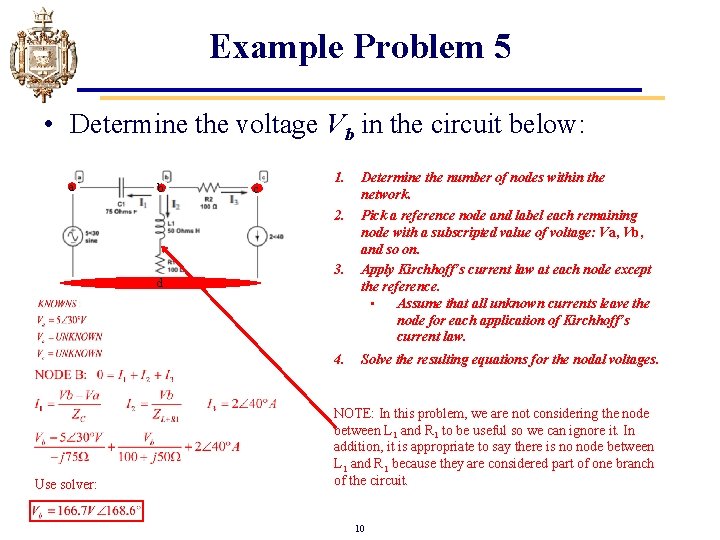
Example Problem 5 • Determine the voltage Vb in the circuit below: a b d Use solver: c 1. Determine the number of nodes within the network. 2. 3. Pick a reference node and label each remaining node with a subscripted value of voltage: Va, Vb, and so on. Apply Kirchhoff’s current law at each node except the reference. • Assume that all unknown currents leave the node for each application of Kirchhoff’s current law. 4. Solve the resulting equations for the nodal voltages. NOTE: In this problem, we are not considering the node between L 1 and R 1 to be useful so we can ignore it. In addition, it is appropriate to say there is no node between L 1 and R 1 because they are considered part of one branch of the circuit. 10

QUESTIONS? 11