Lesson 18 Lines Angles Applying the Pythagorean Theorem

Lesson 18 Lines & Angles Applying the Pythagorean Theorem

Warm-Up Determine if each set of numbers forms a right triangle. 1. 8, 15, 17 2. 4, 5, 6 3. 5, 10, 12 4. 3. 2, 6, 6. 8

Applying the Pythagorean Theorem Target: Apply the Pythagorean Theorem to solve problems in two and three dimensions.

Solving Application Problems 1. Draw a diagram to represent the situation. 2. Label the diagram with the given measures. 3. Solve for the missing measure. Label the answer.

Example 1 An 8 foot ladder is placed 3. 5 feet from the base of a wall. How high up the wall will the ladder reach? Round to the nearest tenth. Draw a diagram. Substitute known values into the Pythagorean Theorem. Simplify by squaring. Subtract 12. 25 from both sides. Square root both sides. The ladder will reach approximately 7. 2 feet up the wall.

Example 2 A ship travels 320 miles due north and then makes a turn due east. It travels 200 miles east. How far is the ship from its starting point? Round to the nearest mile. Use the Pythagorean Theorem. Simplify by squaring. Add. Square root both sides. Round to the nearest whole number. The ship is approximately 377 miles from it’s starting point.

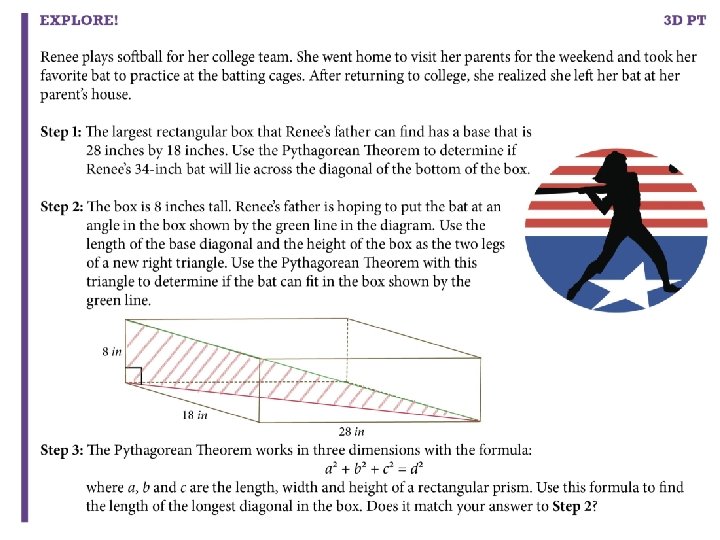
The Pythagorean Theorem in Three Dimensions � In a rectangular prism, the length of the longest diagonal d squared is equal to the sum of the squares of the length a, the width b and the height c of the prism.

Example 3 What is the longest object that Simone can put in a rectangular box that is 10 inches wide, 12 inches long and 20 inches tall? Round to the nearest tenth of an inch. Write three-dimensional formula. Substitute known values. Simplify by squaring. Add. Square root both sides. Round to nearest tenth. The longest object that can fit in the box is about 25. 4 inches.

Exit Problems 1. A 10 -foot ladder leans 9 feet up a wall. How far from the wall is the base of ladder? 2. A shipping company sells a rectangular box with dimensions of 12 inches by 18 inches. Find the length of the longest diagonal in the box.

Communication Prompt � Write your own application problem that uses the Pythagorean Theorem in two or three dimensions. Solve your problem.