LESSON 16 THE CHISQUARE DISTRIBUTION Outline Sampling distribution

LESSON 16: THE CHI-SQUARE DISTRIBUTION Outline • Sampling distribution of the variance • The Chi-Square distribution 1

SAMPLING DISTRIBUTION OF THE VARIANCE • Which supplier is better? – One who usually delivers items in a short time, but does not have consistency and often take very long time eventually causing a huge financial loss to the company. – Or the one who always delivers items after a long but reasonable period of time. – The first supplier’s lead time has a smaller mean, but larger variance (or standard deviation). – The second supplier’s lead time has a larger mean, but smaller variance (or standard deviation). – The final decision may be dictated by any of mean or variance. 2

SAMPLING DISTRIBUTION OF THE VARIANCE • We have seen before that sample parameter is used to draw inference about population parameter. Sample parameter is used to draw inference about population parameter. • Similarly, sample parameter is used to draw inference about the population parameter. 3

THE CHI-SQUARE DISTRIBUTION • Assumptions: – The chi-square distribution assumes that the sample observations are drawn form a normally distributed population. – The chi-square distribution often serves as a satisfactory assumption to the true sampling distribution even when the population is not normal. 4
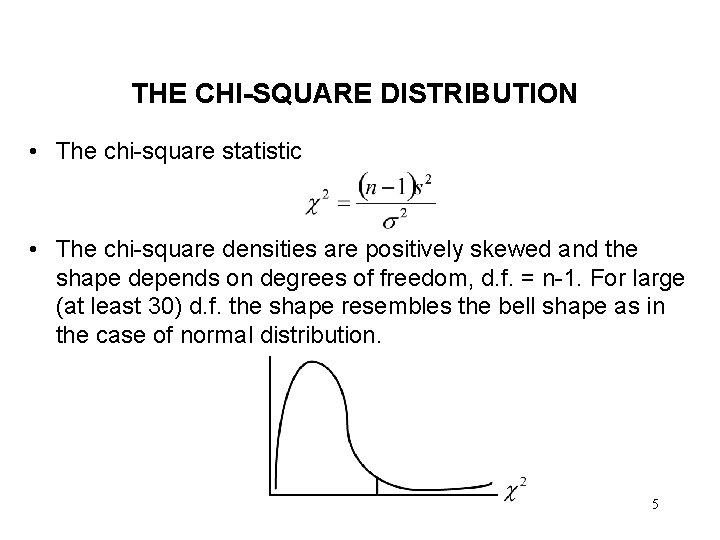
THE CHI-SQUARE DISTRIBUTION • The chi-square statistic • The chi-square densities are positively skewed and the shape depends on degrees of freedom, d. f. = n-1. For large (at least 30) d. f. the shape resembles the bell shape as in the case of normal distribution. 5
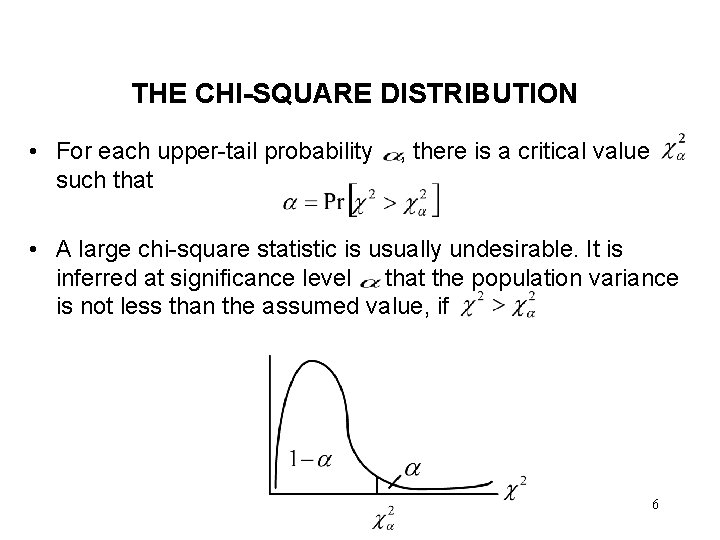
THE CHI-SQUARE DISTRIBUTION • For each upper-tail probability such that , there is a critical value • A large chi-square statistic is usually undesirable. It is inferred at significance level that the population variance is not less than the assumed value, if 6
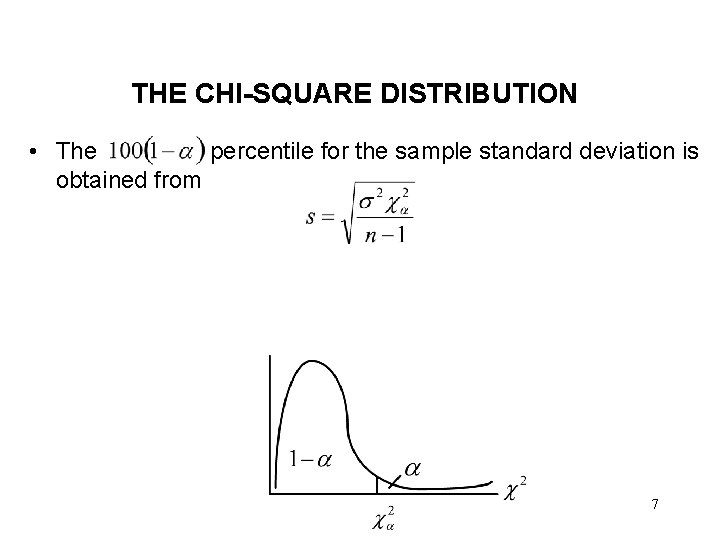
THE CHI-SQUARE DISTRIBUTION • The percentile for the sample standard deviation is obtained from 7

THE CHI-SQUARE DISTRIBUTION • Table H, Appendix A, pp. 542 -543 gives the critical chisquare value for given d. f. and upper tail area. Notice that the table does not contain values for the large samples. Use normal approximation with to Chi-square distribution for large sample (30 or more). • The relevant Excel commands are CHIDIST and CHIINV • CHIDIST (critical value, d. f. ) returns the upper tail area • CHIINV (upper tail area, d. f. ) returns the critical chi-square value. Thus, CHIINV does the same job as Table H. 8

THE CHI-SQUARE DISTRIBUTION Example 1: Determine the upper-tail critical values for the chisquare statistic in the following cases: a. b. 9

THE CHI-SQUARE DISTRIBUTION Example 2: The waiting time of time-sharing jobs for access to a central processing unit is believed to be normally distributed with unknown mean and standard deviation. Find the 70 th percentile for the sample standard deviation when a sample of size is taken and assuming that the true value of the population standard deviation is minutes. 10

THE CHI-SQUARE DISTRIBUTION Example 3: The mean sitting height of adult males may be assumed to be normally distributed, with mean 35” and standard deviation 1. 2”. For a sample size of men, determine the probabilities for a possible level of the sample standard deviation 11

READING AND EXERCISES Lesson 16 Reading: Section 9 -6, pp. 286 -289 Exercises: 9 -35, 9 -36, 9 -37, 9 -39 12
- Slides: 12