Lesson 16 Series AC Circuits 1 Learning Objectives

Lesson 16: Series AC Circuits 1

Learning Objectives • Compute the total impedance for a series AC circuit. • Apply Ohm’s Law, Kirchhoff’s Voltage Law and the voltage divider rule to AC series circuits. • Graph impedances, voltages and current as a function of phase. • Graph voltages and current as a function of time. 2

Impedance • Recall that impedance is a complex quantity that can be made up of Resistance (R) (real part) and Reactance (X) (imaginary part). • Unit of impedance is Ohms ( ). Z X q R 3

Resistors • For resistors, voltage and current are in phase: 4
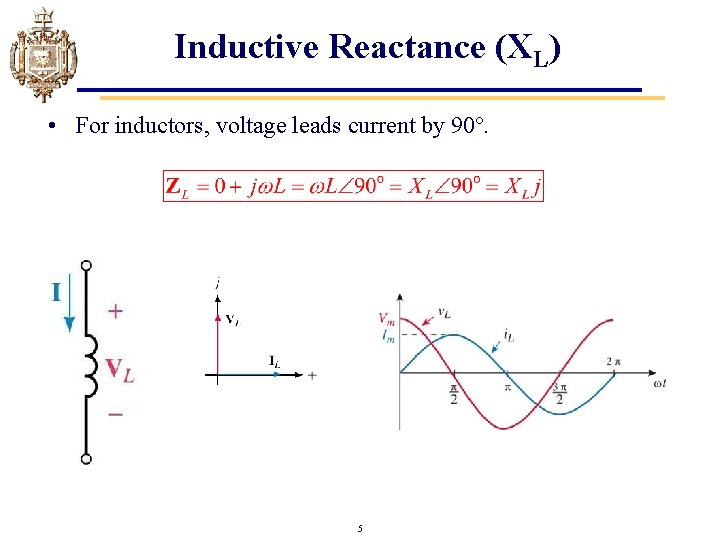
Inductive Reactance (XL) • For inductors, voltage leads current by 90º. 5
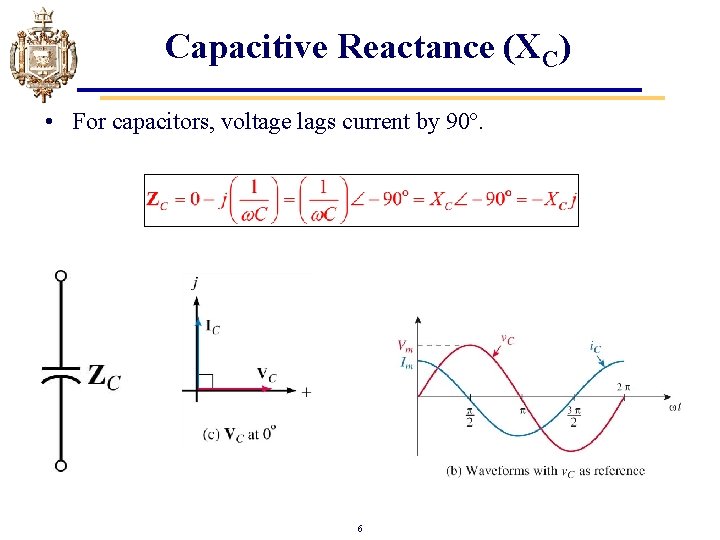
Capacitive Reactance (XC) • For capacitors, voltage lags current by 90º. 6

Impedance • Because impedance is a complex quantity, it can be represented graphically in the complex plane. ZR = R 0º = R + j 0 = R ZL = XL 90º = 0 + j. XL = j. XL ZC = XC -90º = 0 - j. XC = -j. XC 7
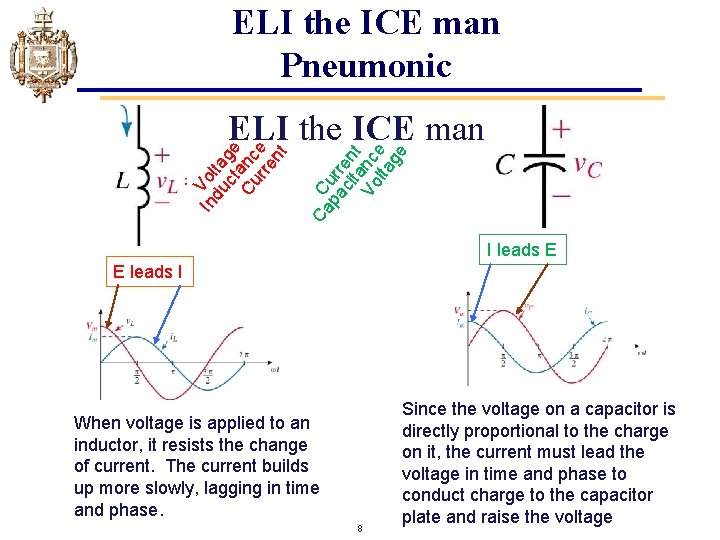
ELI the ICE man Pneumonic Ca C pa urr cit en a t Vo nc lta e ge In Vol du ta ct ge Cu anc rre e nt ELI the ICE man I leads E E leads I When voltage is applied to an inductor, it resists the change of current. The current builds up more slowly, lagging in time and phase. 8 Since the voltage on a capacitor is directly proportional to the charge on it, the current must lead the voltage in time and phase to conduct charge to the capacitor plate and raise the voltage

Solving complex EE problems 1. Convert sine waves to phasors. 2. Perform multiplication/division if needed. 3. Convert phasors to complex numbers if needed to perform addition/subtraction. 4. Convert back to phasor form for the answer to the problem. 9

Important Notes • Peak values are useful for time domain representations of signals. • RMS values are the standard when dealing with phasor domain representations. • If you need to represent something in the time domain, you will need to convert RMS->Peak voltage to obtain Em. 10
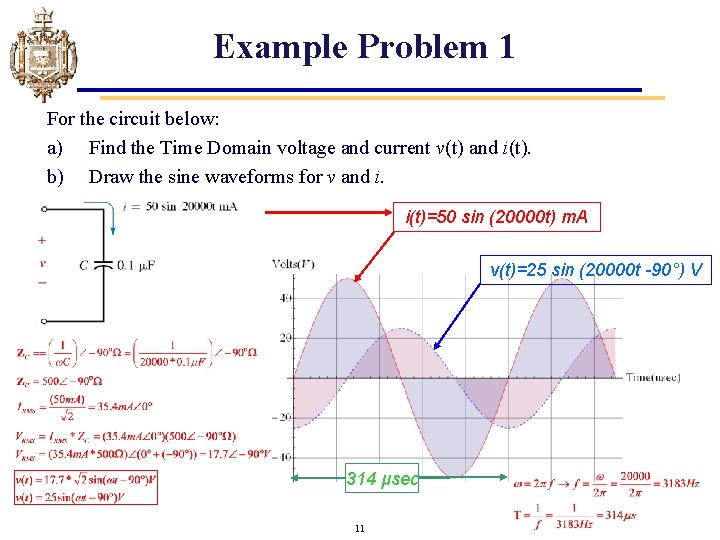
Example Problem 1 For the circuit below: a) Find the Time Domain voltage and current v(t) and i(t). b) Draw the sine waveforms for v and i. i(t)=50 sin (20000 t) m. A v(t)=25 sin (20000 t -90°) V 314 μsec 11

AC Series Circuits • Total impedance is sum of individual impedances. • Also note that current is the same through each element. 12
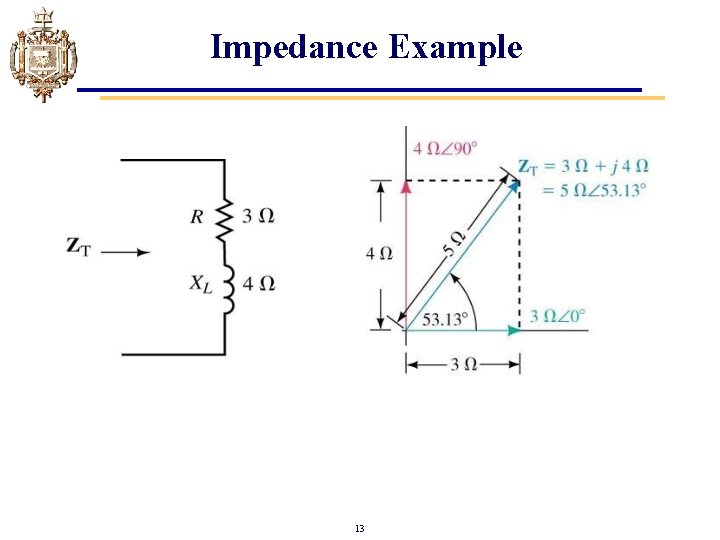
Impedance Example 13

Impedance Example For the circuit below find ZT. Recall: ZR = R 0º = R + j 0 = R ZL = XL 90º = 0 + j. XL = j. XL ZC = XC -90º = 0 - j. XC = -j. XC 14

Special case of Impedance • Whenever a capacitor and inductor of equal reactances are placed in series, the equivalent circuit is a short circuit. 15

Impedance • If the total impedance has only a real component, the circuit is said to be resistive (X = 0 or = 0°). • But since − If > 0°, the circuit is inductive. ELI − If < 0°, the circuit is capacitive. ICE 16
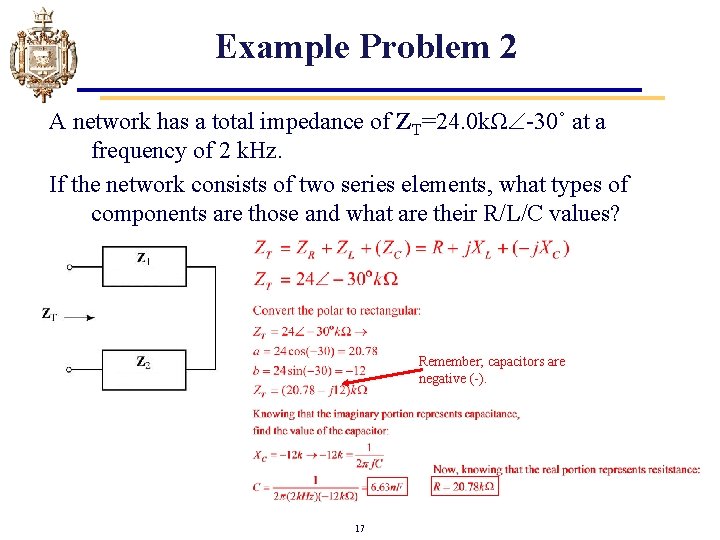
Example Problem 2 A network has a total impedance of ZT=24. 0 kΩ -30˚ at a frequency of 2 k. Hz. If the network consists of two series elements, what types of components are those and what are their R/L/C values? Remember; capacitors are negative (-). 17
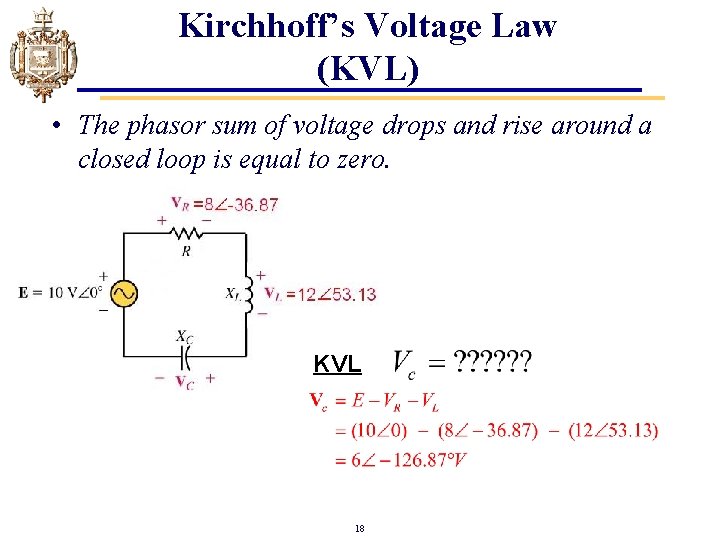
Kirchhoff’s Voltage Law (KVL) • The phasor sum of voltage drops and rise around a closed loop is equal to zero. KVL 18
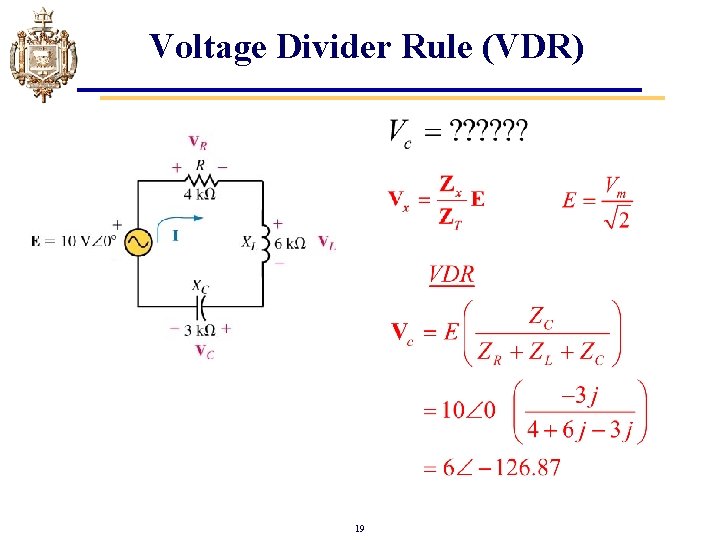
Voltage Divider Rule (VDR) 19

Example Problem 3 es(t)=170 sin (1000 t + 0) V. • Determine ZTOT • Determine total current ITOT • Determine voltages VR, VL, and Vc • Verify KVL for this circuit • Graph E, VL, VC, VR in the time domain 20
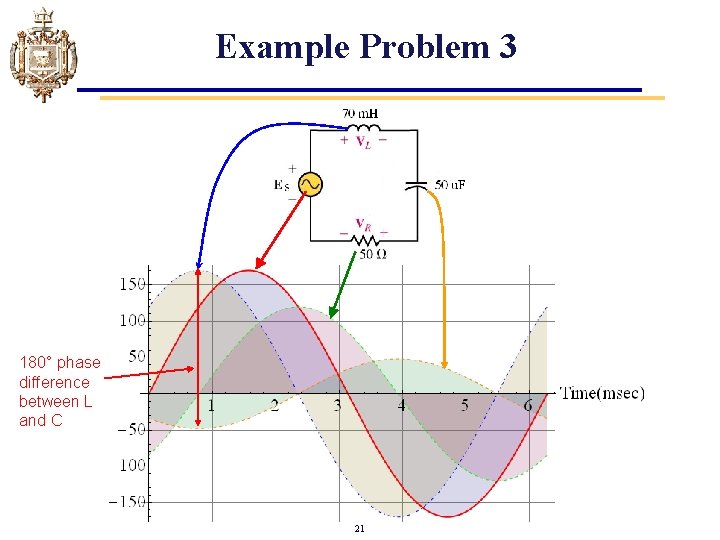
Example Problem 3 180° phase difference between L and C 21

Example Problem 4 es(t)=294 sin (377 t + 0) V. • Use the voltage divider rule to find VL • Determine the value of inductance 22

QUESTIONS? 23
- Slides: 23