Lesson 15 Relations and algebras Compiled by Ondej

Lesson 15: Relations and algebras Compiled by: Ondřej Kohut (within the Theory of formal systems course)

Contents § Theory of sets (revision) § Relations and mappings (revision) – – – Relations Binary relations on a set Mappings Partitions, equivalences Orderings § Algebras – Algebras with one operation – Algebras with two operations – Lattices 9/17/2020 Relace a algebry 2

Naive theory of sets § Language: • Special symbols: – Binary predicates: (is an element of), (is a proper subset of), (is a subset of) – Binary function symbols: (intersection), (union) § Cantor – the naive set theory (without axiomatization) § There are many formal axiomatizations, but none of them is complete. § Examples: von Neumann-Bernays-Gödel, Zermelo-Fränkel + axiom of choice 9/17/2020 Relace a algebry 3

Zermelo-Fränkel set-theory Axiom of extensionality: Two sets are the same if and only if they have the same elements. Axiom of empty set: There is a set with no elements. Axiom of pairing: If x, y are sets, then so is {x, y}, a set containing x and y as its only elements. Axiom of union: Every set has a union. That is, for any set x there is a set y whose elements are precisely the elements of x. Axiom of infinity: There exists a set x such that {} is in x and whenever y is in x, so is the union y U {y}. Axiom of separation (or subset axiom): Given any set and any proposition P(x), there is a subset of the original set containing precisely those elements x for which P(x) holds. Axiom of replacement: Given any set and any mapping, formally defined as a proposition P(x, y) where P(x, y) and P(x, z) implies y = z, there is a set containing precisely the images of the original set's elements. Axiom of power set: Every set has a power set. That is, for any set x there exists a set y, such that the elements of y are precisely the subsets of x. Axiom of regularity (or axiom of foundation): Every non-empty set x contains some element y such that x and y are disjoint sets. Axiom of choice: (Zermelo's version) Given a set x of mutually disjoint nonempty sets, there is a set y (a choice set for x) containing exactly one element from each member of x. 9/17/2020 Relace a algebry 4

Naive theory of sets § Ø – an empty set § Cardinality of a set A: |A| Relations between sets (axioms): § Equality § Inclusion 9/17/2020 Relace a algebry 5

Naive theory of sets – set theoretical operations § Intersection § Union § Difference § Symetrical difference § Complement with respect to universe U 9/17/2020 Relace a algebry 6

Naive theory of sets – set theoretical operations § Potential set § Cartesian product § Cartesian power n A 1=A, A 0={Ø} 9/17/2020 Relace a algebry 7

Relations § n-ary relation between the sets A 1, A 2, . . . , An § Examples: – D = a set of possible days – M = a set of VŠB rooms – Z = a set of VŠB employees A ternary relation meeting (when, where, who): 9/17/2020 Relace a algebry 8

Binary relations § Inverse relation to r: § Composition of relations 9/17/2020 Relace a algebry 9

Binary relations A binary relation r on a set A is called: § Reflexive: x A: (x, x) r § Irreflexive: x A: (x, x) r § Symmetric: x, y A: (x, y) r (y, x) r § Antisymmetric: x, y A: (x, y) r and (y, x) r x=y § Asymmetric: x, y A: (x, y) r (y, x) r § Transitive: x, y, z A: (x, y) r and (y, z) r (x, z) r § Cyclic: x, y, z A: (x, y) r and (y, z) r (z, x) r § Linear: x, y A: x=y or (x, y) r or (y, x) r 9/17/2020 Relace a algebry 10

Binary relations The important types of binary relations: § Tolerance – reflexive, symmetric § Quasi-ordering – reflexive, transitive § Equivalence – reflexive, symmetric, transitive § Partial ordering – reflexive, antisymmetric, transitive 9/17/2020 Relace a algebry 11

Binary relations Examples: § Tolerance: – „to be akin to“ on a set of people, – „to have a different age no more than one year“ on the set of people, . . . § Quasi-ordering: – „if it holds |X| |Y|, then sets X and Y are in relation“ on a set of sets, – divisibility relation on a set of integers, – „not to be older“ on the set of people, . . . § Equivalence: – „to be the same age“ on the set of people, – equivalence on a set of natural numbers, . . . § Ordering: – inclusion relation, – divisibility relation on the set of natural numbers, . . . 9/17/2020 Relace a algebry 12

Mappings (functions) § f A B is called a mapping from a set A into a set B (partial mapping), iff: ( x A, y 1, y 2 B) ( (x, y 1) f and (x, y 2) f y 1 = y 2 ) § f is called a mapping of a set A into a set B (total mapping, written as: f: A B), iff: – f is mapping from A to B – ( x A)( y A) ( (x, y) f) § If f is a mapping and (x, y) f, then we write: f(x)=y 9/17/2020 Relace a algebry 13

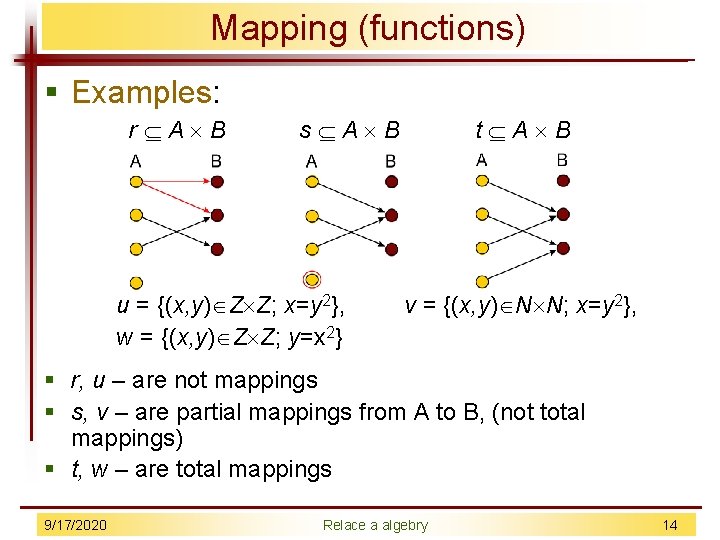
Mapping (functions) § Examples: r A B s A B u = {(x, y) Z Z; x=y 2}, w = {(x, y) Z Z; y=x 2} t A B v = {(x, y) N N; x=y 2}, § r, u – are not mappings § s, v – are partial mappings from A to B, (not total mappings) § t, w – are total mappings 9/17/2020 Relace a algebry 14

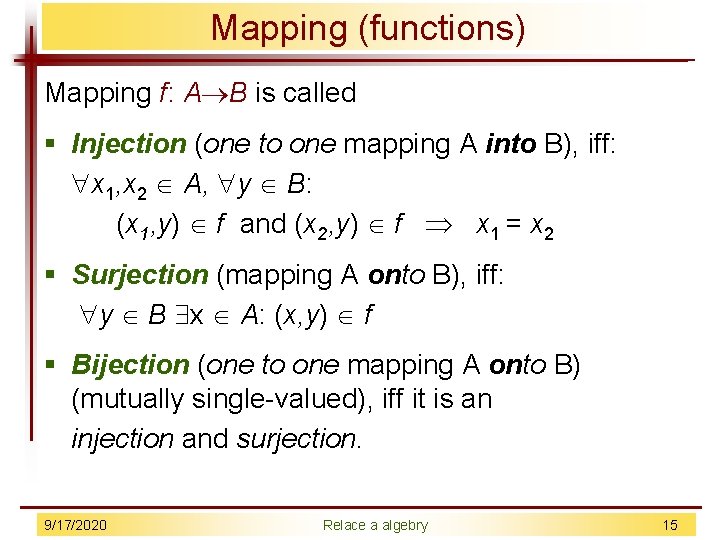
Mapping (functions) Mapping f: A B is called § Injection (one to one mapping A into B), iff: x 1, x 2 A, y B: (x 1, y) f and (x 2, y) f x 1 = x 2 § Surjection (mapping A onto B), iff: y B x A: (x, y) f § Bijection (one to one mapping A onto B) (mutually single-valued), iff it is an injection and surjection. 9/17/2020 Relace a algebry 15

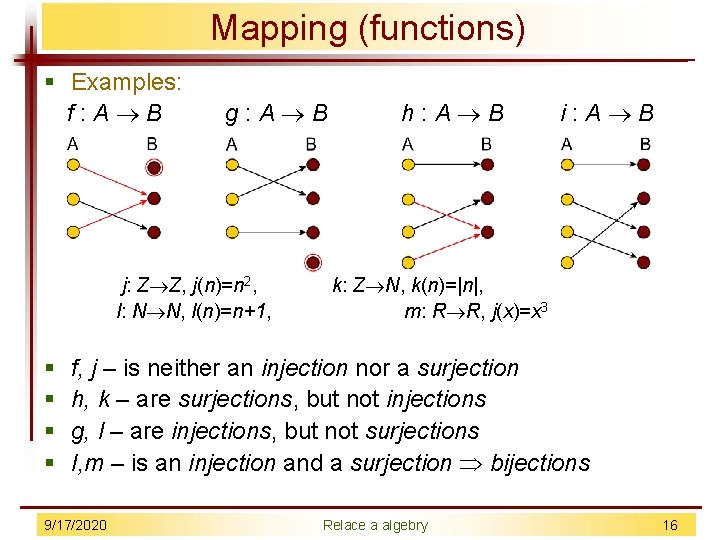
Mapping (functions) § Examples: f : A B § § g : A B j: Z Z, j(n)=n 2, l: N N, l(n)=n+1, h : A B i : A B k: Z N, k(n)=|n|, m: R R, j(x)=x 3 f, j – is neither an injection nor a surjection h, k – are surjections, but not injections g, l – are injections, but not surjections I, m – is an injection and a surjection bijections 9/17/2020 Relace a algebry 16

Partitions and equivalences § Partition on a set A is such a system that: X = { Xi; i I } – Xi A pro i I – Xi Xj = Ø pro i, j I, i j – U X = A Xi – classes of the partition § Refininment of a partition X = { Xi; i I } is a system that: Y = { Yj; j J }, iff: – j J, i I so that Yj Xi 9/17/2020 Relace a algebry 17

Partitions and equivalences § Let r be an equivalence relation on a set A, X is a partition on A, then it holds: § Xr = {[x]r; x A} – the partition on A (the partition induced by equivalence r, the factor set of the set A according to the equivalence r) § r. X = {(x, y); x and y belongs to the same class of the partition X} – equivalence on A (induced by partition X) Examples: § r Z Z; r = {(x, y); 3 divides x-y } X={X 1, X 2, X 3} § X 1={…-6, -3, 0, 3, 6, …} § X 2={…-5, -2, 1, 4, 7, …} § X 3={…-4, -1, 2, 5, 8, …} 9/17/2020 Relace a algebry 18

Orderings § If r is an order relation on A, then a couple (A, r) is called an ordered set § Written as: (A, ) – Examples: (N, ), (2 M, ) § Cover relation Let (A, ) be an ordered set, (a, b) A a –< b („b covers a“), iff: a < b and c A: a c a c b – Examples: (N, ), –< ={(n, n+1); n N} 9/17/2020 Relace a algebry 19

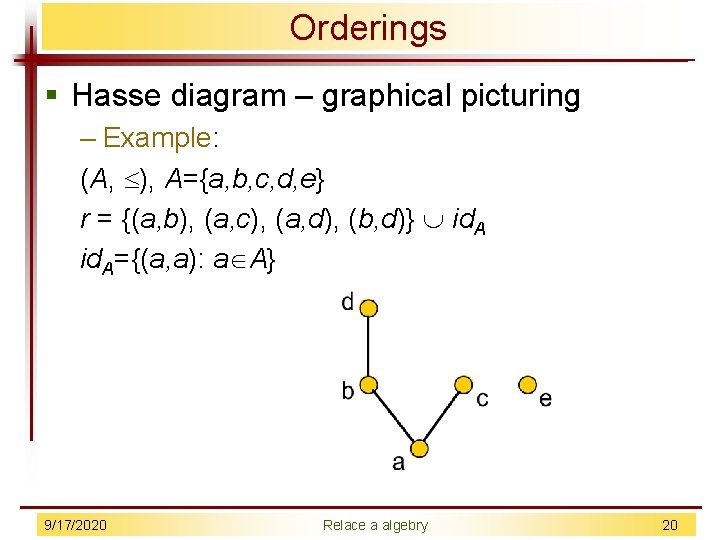
Orderings § Hasse diagram – graphical picturing – Example: (A, ), A={a, b, c, d, e} r = {(a, b), (a, c), (a, d), (b, d)} id. A={(a, a): a A} 9/17/2020 Relace a algebry 20

Orderings An element a of an ordered set (A, ) is called: § The least: for x A: a x § The greatest: for x A: x a § Minimal: for x A: (x a x = a) § Maximal: for x A: (a x x = a) § Examples: – – The least: does not exist The greatest: does not exist Minimal: a, e Maximal: d, c, e 9/17/2020 Relace a algebry 21

Orderings § A mapping of the ordered sets (A, ), (B, ) is called isomorphic, iff the bijection f: A B exists such that: x, y A: x y, iff f(x) f(y) § A mapping of the ordered sets (A, ), (B, ) is called isotone f: A B, when it holds: x, y A: x y f(x) f(y) § Examples: § f: N Z, f(x)=kx, k Z, k 0 is isotone § g: N Z, g(x)=kx, k Z, k 0 is not isotone 9/17/2020 Relace a algebry 22

Orderings § Let (A, ) be an ordered set, M A, then § LA(M)={x A; m M: x m } – A set of lower bounds § UA(M)={x A; m M: m x } – A set of upper bounds § Inf. A(M) – The greatest element of the set LA(M) – Infimum of the set M § Sup. A(M) – The least element of the set UA(M) – Supremum of the set M 9/17/2020 Relace a algebry 23

Lattices - lattice ordered sets § A set (A, ) is called a lattice (lattice ordered set), iff: x, y A s, i A : s = sup({x, y}), i = inf({x, y}) § Notation: – x y = sup({x, y}) – x y = inf({x, y}) § If sup(M) a inf(M) exist for every M A, then (A, ) is called a complete lattice 9/17/2020 Relace a algebry 24

Algebras Algebra (abstract algebra) is couple: (A, FA): § A Ø – an underlying set of algebra § FA = {fi: Ap(fi) A; i I} – a set of operations on A § p(fi) – an arity of operation fi § Examples: – (N, +2, 2) the set of natural numbers with the addition and multiplication operations – (2 M, , ) the set of all subsets of a set M with the intersection and union operations – (F, , ) The set (F) of the propositional logic formulas with the conjunction and disjunction operations 9/17/2020 Relace a algebry 25

Algebras with one binary operation Grupoid G=(G, ) § : G G G § If a set G is finite, then the grupoid G is called finite § Order of a grupoid = |G| Examples of grupoids: § G 1=(R, +), G 2=(R, ), G 3=(N, +). . . 9/17/2020 Relace a algebry 26

Algebras with one binary operation § We can express the finite grupoid G=(G, ) by Cayley table § Example: § G = {a, b, c} a b c a a b c b a c c c a a b § For example: a b = b, b a = a, c c = b . . . 9/17/2020 Relace a algebry 27

Algebras with one binary operation Let G=(G, ) is grupoid, G is called: § Commutative, if it holds: – ( a, b G)(a b = b a) § Associative, if it holds: – ( a, b, c G)((a b) c = a (b c)) § With a neutral element, if it holds: – ( e G a G)(a e = a = e a) § With an aggressive element, if it holds: – ( o G a G)(a o = o a) § With inverse elements, if it holds: – ( a G b G)(a b = e = b a) 9/17/2020 Relace a algebry 28

Algebras with one binary operation Examples: § (R, ), (N, +) – commutative and associative § (R, ), a b = (a+b) / 2 – commutative, not associative § (R, ), a b = ab – neither commutative nor associative § (R, ) – 1 = the neutral element, 0 = the aggressive element 9/17/2020 Relace a algebry 29

Algebras with one binary operation Let G=(G, G) be a grupoid. H G is called closed (with respect to the operation G), if it holds: § ( a, b H)(a G b H) A Grupoid H=(H, H) is a subgrupoid of a grupoid G=(G, G), if it holds: § Ø H G is closed § a, b H: a H b = a G b § Examples: § (N, +N) is a subgrupoid of (Z, +Z) § {0, 1, 2} is not the base set of a podgrupoid (Z, +Z) 9/17/2020 Relace a algebry 30

Algebras with one binary operation § Let G 1=(G 1, 1), G 2=(G 2, 2) be a grupoids. § G 1 G 2 =(G 1 G 2, ) – direct product G 1 and G 2, where: § (a 1, a 2) (b 1, b 2) = (a 1 1 b 1, a 2 2 b 2) Examples: § G 1=(Z, +), G 2=(Z, ). § G 1 G 2 =(Z Z, ), § (a 1, a 2) (b 1, b 2) = (a 1 + b 1, a 2 b 2) § (1, 2)(3, 4) = (1+3, 2 4) = (4, 8) and so on. 9/17/2020 Relace a algebry 31

Algebras with one binary operation § Let G =(G, G), H =(H, H) be grupoids and h: G H be a mapping. § h is called homomorphism of grupoid G into grupoid H, if it holds: § a, b G: h(a G b) = h(a) H h(b) The types of homomorphism: § Monomorphism – h is injective § Epimorphism – h is surjective § Isomorphism – h is bijective § Endomorphism – H=G § Automorphism – is bijective and H=G Examples: § (R, +), h(x)= -x , h is automorfismus (R, +) into itself § h(x+y) = -(x+y) = (-x) + (-y) = h(x) + h(y) 9/17/2020 Relace a algebry 32

Algebras with one binary operation r is called a congruence on a grupoid G=(G, G), iff: § r is a binary relation: θ G G § r is an equivalence § (a 1, a 2), (b 1, b 2) r (a 1 G b 1, a 2 G b 2) r A factor grupoid of grupoid G according to the congruence r: G/r=(G/r, G/r), [a]r G/r [b]r = [a G b]r Examples: [0] § r Z Z; r = {(x, y); 3 divides x-y } [1] § r is a congruence on (Z, +) [2] 9/17/2020 Relace a algebry [0] [1] [2] [0] [2] [0] [1] 33

Algebras with one binary operation The types of grupoids: § Semigroup – an associative grupoid § Monoid – a semigroup with the neutral element § Group – a monoid with the inverse elements § Abelian group – a commutative group Examples: § (Z, –) – grupoid, not a semigroup § (N – {0}, +) – semigroup, not a monoid § (N, ) – monoid, not a group § (Z, +) – Abelian group 9/17/2020 Relace a algebry 34

Algebras with two binary operation Algebra (A, +, ·) is called a Ring, if it holds: § (A, +) is commutative group § (A, ·) is monoid § For a, b, c A it holds: a·(b+c)=a·b+a·c, (b+c)·a=b·a + c·a § If |A|>1, then (A, +, ·) is called a non-trivial ring. § Let 0 A is the neutral element of group (A, +). Then 0 is called the ring zero (A, +, ·). § Let 1 A is the neutral element of monoid (A, ·). Then 1 is called the ring unit (A, +, ·). 9/17/2020 Relace a algebry 35

Algebras with two binary operation A ring (A, +, ·) is called a field, if it holds: § (A - {0}, ·) is a commutative group Examples: § (Z, +, ·) – a ring, not a field § (R, +, ·), (C, +, ·) – fields 9/17/2020 Relace a algebry 36

Lattice – algebraic structure § Lattice L = (L, , ) § : L L L, : L L L § x, y, z L it holds: x x = x idempotention x y = y x commutativity x (y z) = (x y) z x (x y) = x 9/17/2020 Relace a algebry associativity absorption 37

Lattice – algebraic structure Let (A, , ) be a lattice, (B, ) be a lattice ordered set § Let us define a relation on A : a b, iff a b = b § Let us define the relations and on B a b = sup{a, b}, a b = inf{a, b}, Then it holds: § (A, ) is a lattice ordered set, where: sup{a, b}= a b, inf{a, b}= a b § (B, , ) is a lattice § (A, , ) = (A, , ) 9/17/2020 Relace a algebry 38

Lattice – algebraic structure A lattice (L, , ) is called: § Modular, if it holds: x, y, z L : x z x (y z) = (x y) z § Distributive, if it holds: x, y, z L : x (y z) = (x y) (x z) § Complementary, if it holds: : There is the least element 0 L and the greatest element 1 L x’ L : x x’ = 0, x x’ = 1 x’ is called a complement of an element x 9/17/2020 Relace a algebry 39

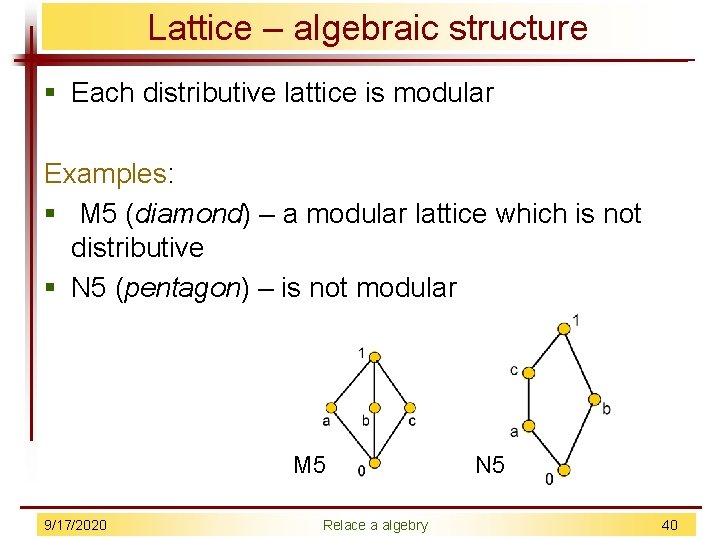
Lattice – algebraic structure § Each distributive lattice is modular Examples: § M 5 (diamond) – a modular lattice which is not distributive § N 5 (pentagon) – is not modular M 5 9/17/2020 Relace a algebry N 5 40

Lattice – algebraic structure Lattice (L, , ) is called Boolean lattice, when it is: § Complementary, distributive, with the least element 0 L and with the greatest element 1 L Boolean algebra: § (L, , , –, 0, 1), – : L L is an operation of complement in L Example: § (2 A, , ), A = {1, 2, 3, 4, 5, 6, 7} 9/17/2020 Relace a algebry 41