lesson 15 band theory using Solid State Physics

lesson # 15: band theory using: Solid State Physics M. Casalboni 2018/’ 19 • Bloch theorem • tools for solve the Schrödringer eq. BAND STRUCTURE let us face the problem to calculate the real band structure of a 3 D crystal we will show only the basic methods without enter in the technicalities 1/22

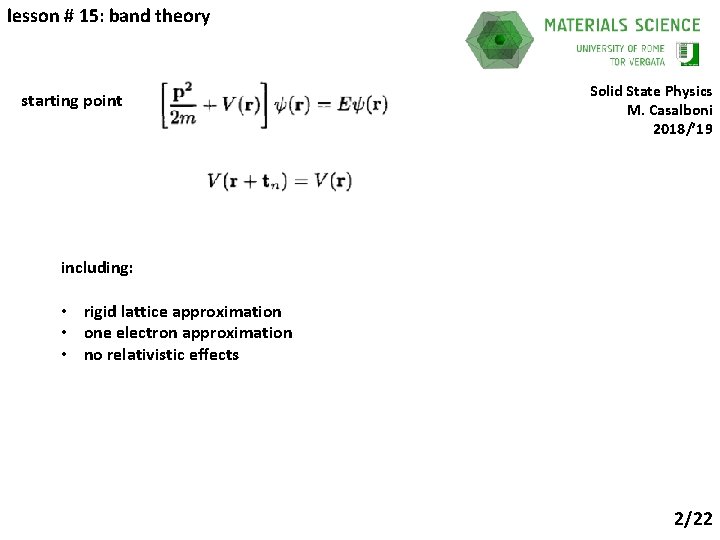
lesson # 15: band theory starting point Solid State Physics M. Casalboni 2018/’ 19 including: • rigid lattice approximation • one electron approximation • no relativistic effects 2/22

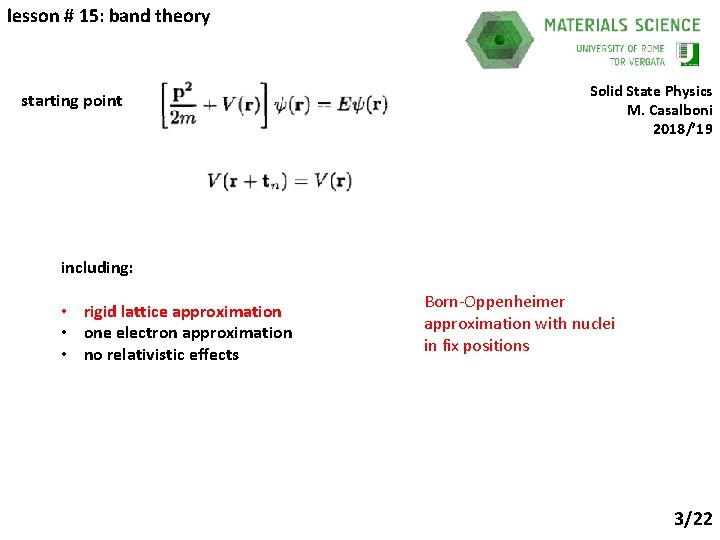
lesson # 15: band theory starting point Solid State Physics M. Casalboni 2018/’ 19 including: • rigid lattice approximation • one electron approximation • no relativistic effects Born-Oppenheimer approximation with nuclei in fix positions 3/22

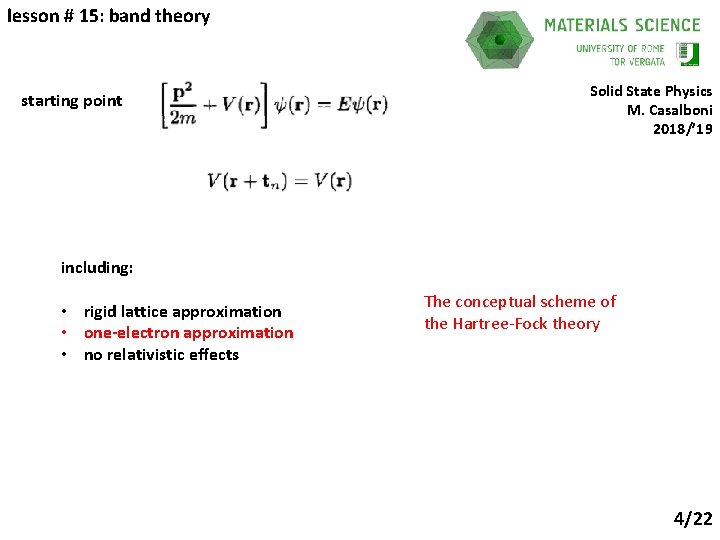
lesson # 15: band theory starting point Solid State Physics M. Casalboni 2018/’ 19 including: • rigid lattice approximation • one-electron approximation • no relativistic effects The conceptual scheme of the Hartree-Fock theory 4/22

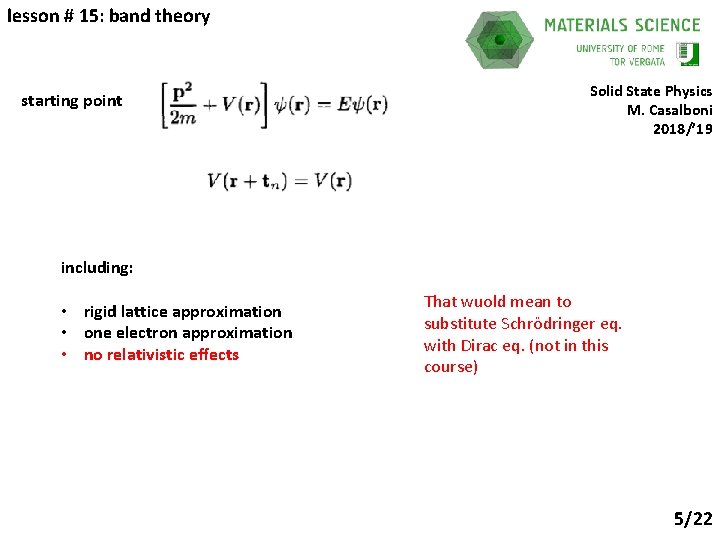
lesson # 15: band theory starting point Solid State Physics M. Casalboni 2018/’ 19 including: • rigid lattice approximation • one electron approximation • no relativistic effects That wuold mean to substitute Schrödringer eq. with Dirac eq. (not in this course) 5/22

lesson # 15: band theory There are different philosophies to approach the calculation of the band structures of crystalline solids: Solid State Physics M. Casalboni 2018/’ 19 6/22

lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 Tight-binding method (LCAO) simple crystal one atom per unit cell 7/22

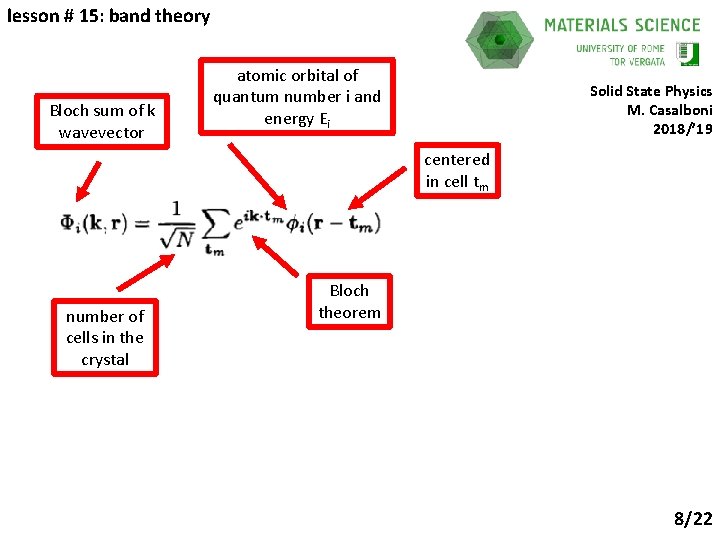
lesson # 15: band theory Bloch sum of k wavevector atomic orbital of quantum number i and energy Ei Solid State Physics M. Casalboni 2018/’ 19 centered in cell tm number of cells in the crystal Bloch theorem 8/22

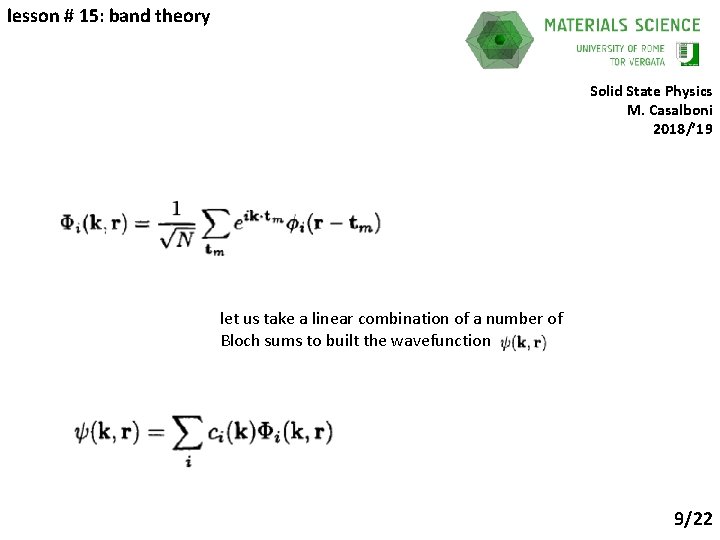
lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 let us take a linear combination of a number of Bloch sums to built the wavefunction 9/22

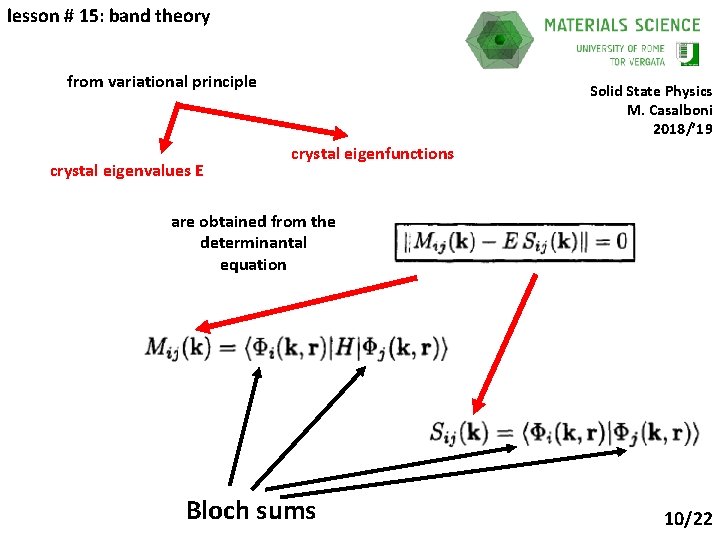
lesson # 15: band theory from variational principle crystal eigenvalues E Solid State Physics M. Casalboni 2018/’ 19 crystal eigenfunctions are obtained from the determinantal equation Bloch sums 10/22

lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 11/22

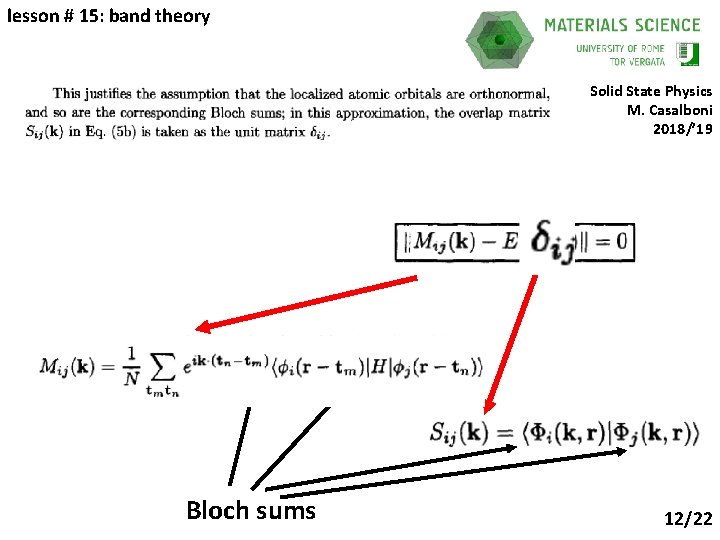
lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 Bloch sums 12/22

lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 only first neighbours 13/22

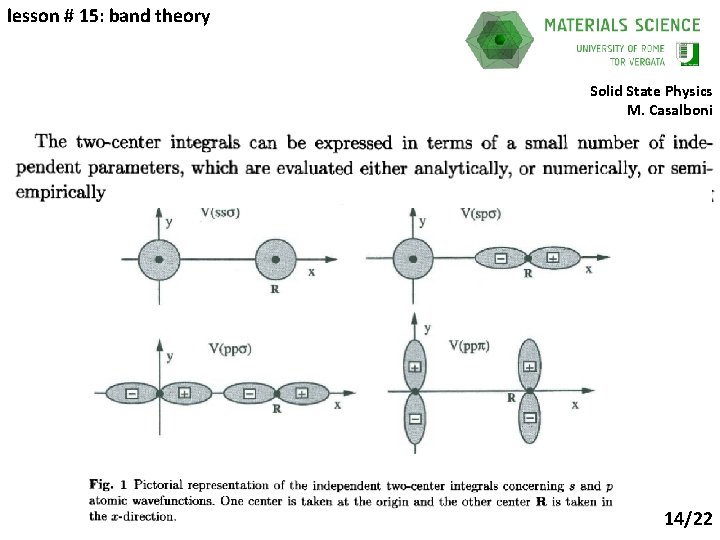
lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 14/22

lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 15/22

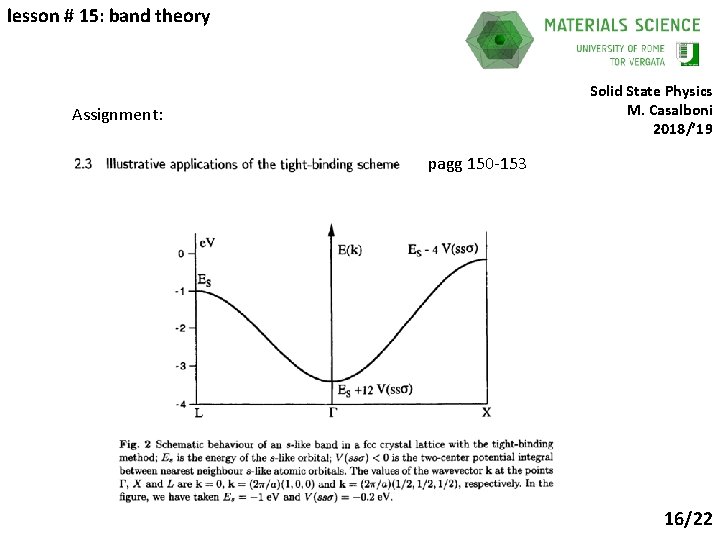
lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 Assignment: pagg 150 -153 16/22

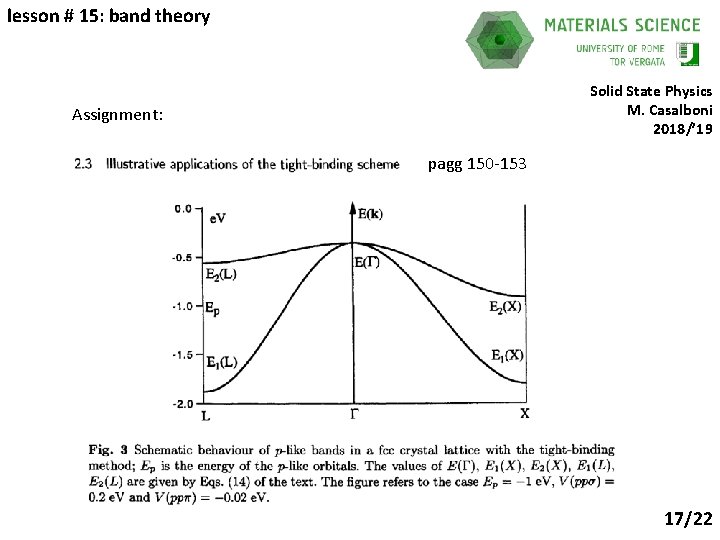
lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 Assignment: pagg 150 -153 17/22

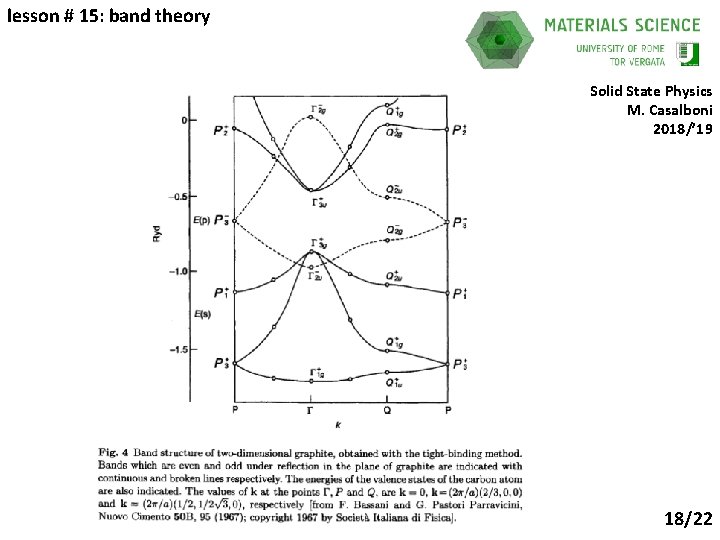
lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 18/22

lesson # 15: band theory Alternately we can take PLANE WAVES as a base for the expansion Solid State Physics M. Casalboni 2018/’ 19 Sommerfeld this can be in principle done BUT in the region of core it needs an INFINITE number of basic funcion to be summed in order to well represent the very localized states we can take advantage from the ortogonal nature of the core states and electron states of interest (outer electrons that make bounds) OPW 19/22

lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 As empirical evolution of OPW method let us illustrate the PSEUDOPOTENTIAL method we take in account the core states in the hamiltonian replacing the TRUE strong crystalline potential with a weak pseudopotential (NON TRUE but) effective for the outer electron + we find for PSEUDOWAVEFUNCTIONS that represent the TRUE wavefunctions of the crystal only outside the core region 20/22

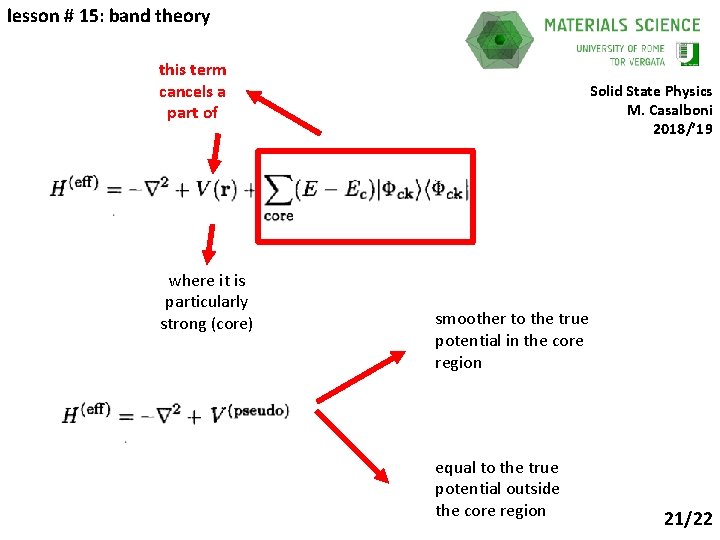
lesson # 15: band theory this term cancels a part of where it is particularly strong (core) Solid State Physics M. Casalboni 2018/’ 19 smoother to the true potential in the core region equal to the true potential outside the core region 21/22

lesson # 15: band theory Solid State Physics M. Casalboni 2018/’ 19 22/22