Lesson 124 Conditions of Congruence Proofs of Congruence

A triangle has three sides and three angles. Two triangles are congruent if any

1. SSS: if the lengths of the sides in one triangle are equal to

2. AAAS: if the angles in one triangle have the same measures as the

3. SAS: if two sides and the included angle in one triangle have the

4. HL: if the lengths of the hypotenuse and a leg in one right

These are also the conditions for triangle similarity. If the lengths in SSS, SAS,

We remember that when we write a statement of similarity or congruence we must

Many proofs require that we show that two segments have equal lengths or that

Example: ______ Given: AD ≅ DB _______ DC AB Outline a______ proof______ that shows:

Answer: ΔADC ≅ ΔBDC by SAS ______ AC ≅ BC by CPCTC

Slides: 17

Download presentation

Lesson 124: Conditions of Congruence, Proofs of Congruence, Isosceles Triangles

A triangle has three sides and three angles. Two triangles are congruent if any one of the four conditions state next are met.

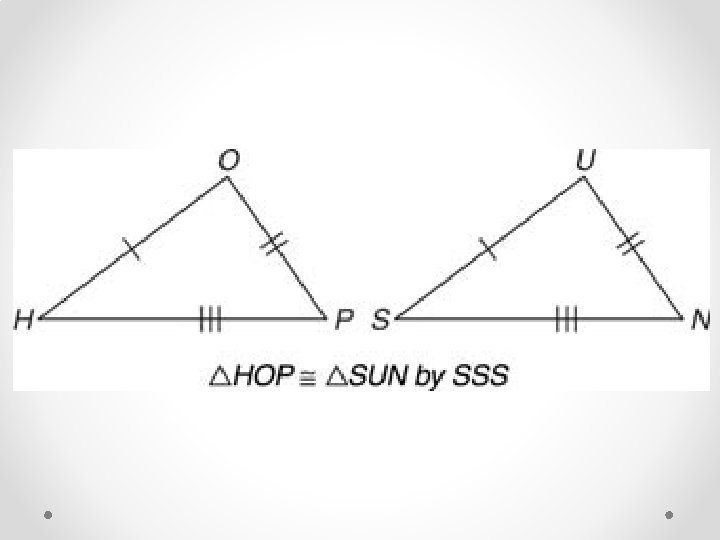
1. SSS: if the lengths of the sides in one triangle are equal to the lengths of the sides in a second triangle, the triangles are congruent. We call this condition side-side (SSS).

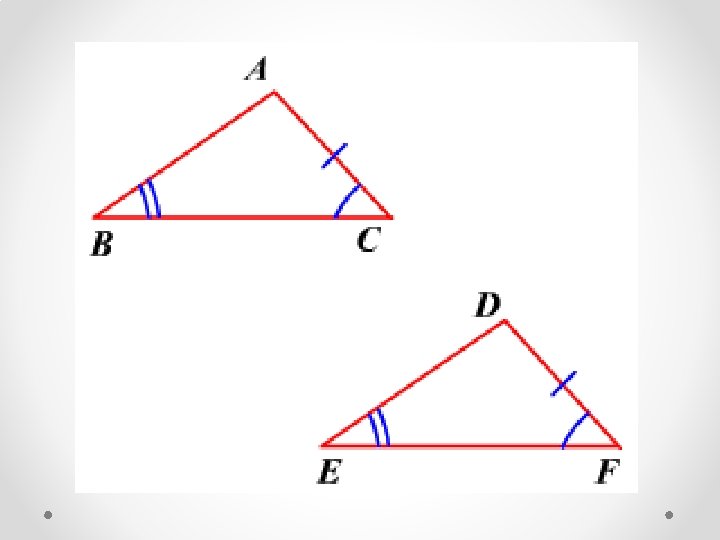
2. AAAS: if the angles in one triangle have the same measures as the angles in a second triangle, the triangles are similar. If a side in one of a pair of similar triangles has the same length as the corresponding side in the other triangle, the scale factor is 1 and the triangles are congruent. We call this condition angle-angle-side (AAAS).

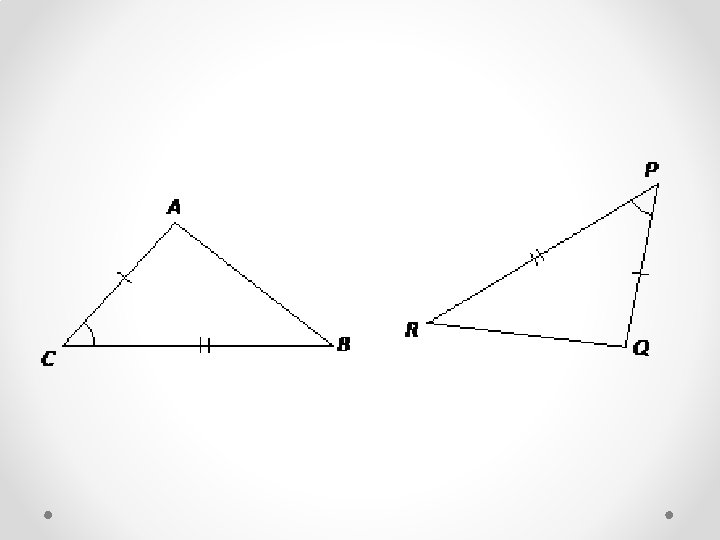
3. SAS: if two sides and the included angle in one triangle have the same measures as two sides and the included angle in a second triangle, the triangles are congruent. We call this condition side-angleside (SAS).

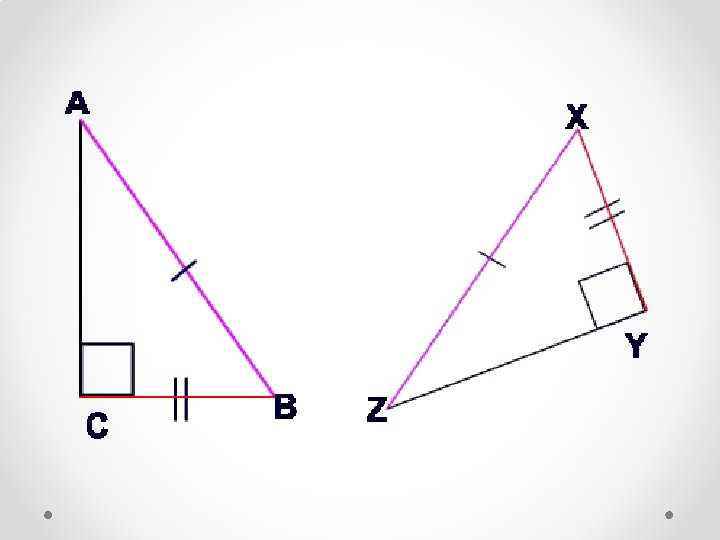
4. HL: if the lengths of the hypotenuse and a leg in one right triangle equal the lengths of the hypotenuse and a leg in a second right triangle, the right triangles are congruent. We call this condition hypotenuse-leg (HL).

These are also the conditions for triangle similarity. If the lengths in SSS, SAS, and HL are not equal but are proportional, the triangles are similar. As a statement of similarity, the “side” in AAAS is unnecessary because AAA is sufficient to designate similarity.

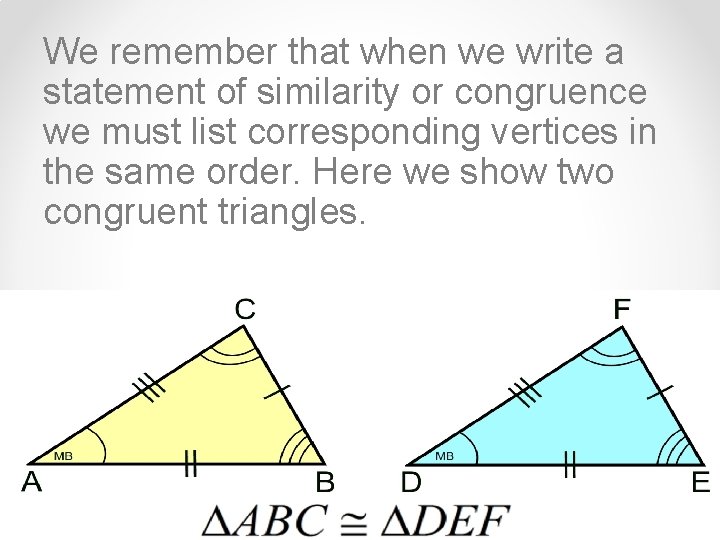
We remember that when we write a statement of similarity or congruence we must list corresponding vertices in the same order. Here we show two congruent triangles.

Many proofs require that we show that two segments have equal lengths or that two angles have equal measures. This is often accomplished by showing that two triangles are congruent. Thus the components have equal measures, because corresponding parts of congruent triangles are congruent (CPCTC). If we can outline a proof first, writing the formal proof is easy. To outline a proof, we first sketch the figure and use tick marks to record the given information on the figure. Then we write the statement of congruence, being careful to list the vertices in corresponding order. Then we write AAAS, SSS, SAS or HL to show why the triangles are congruent.

Example: ______ Given: AD ≅ DB _______ DC AB Outline a______ proof______ that shows: AC ≅ BC

Answer: ΔADC ≅ ΔBDC by SAS ______ AC ≅ BC by CPCTC

Open books to Page 506.

HW: Lesson 124 #1 -30