LESSON 12 8 Congruent and Similar Solids FiveMinute

LESSON 12– 8 Congruent and Similar Solids

Five-Minute Check (over Lesson 12– 7) TEKS Then/Now New Vocabulary Key Concept: Similar Solids Key Concept: Congruent Solids Example 1: Identify Similar and Congruent Solids Theorem 12. 1 Example 2: Use Similar Solids to Write Ratios Example 3: Real-World Example: Use Similar Solids to Find Unknown Values

Over Lesson 12– 7 Name a line not containing point P on the sphere. A. B. C. D.

Over Lesson 12– 7 Name a triangle in the sphere. A. ΔVQS B. ΔRTU C. ΔPQR D. ΔPXW

Over Lesson 12– 7 Name a segment containing point Q in the sphere. A. B. C. D. TU

Over Lesson 12– 7 Tell whether the following statement from Euclidean geometry has a corresponding statement in spherical geometry. If so, write the corresponding statement. If not, explain why. If B is between A and C, then AB + BC = AC. A. Yes, through 2 points there is exactly one line. B. Yes, the points on any great circle or arc of a great circle can be put into one correspondence with real numbers. C. No, AC may not be the distance from A to C through B. It may be the distance the other direction around the sphere.

Over Lesson 12– 7 Which of the following is represented by a line in spherical geometry? A. triangle B. great circle C. radius D. diameter

Targeted TEKS G. 11(D) Apply the formulas for the volume of three-dimensional figures, including prisms, pyramids, cones, cylinders, spheres, and composite figures, to solve problems using appropriate units of measure. Mathematical Processes G. 1(E), G. 1(F)

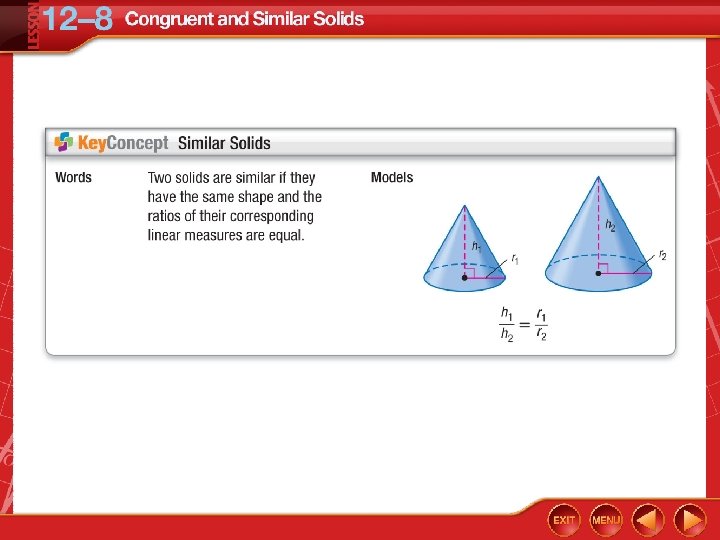
You compared surface areas and volumes of spheres. • Identify congruent or similar solids. • Use properties of similar solids.

• similar solids • congruent solids

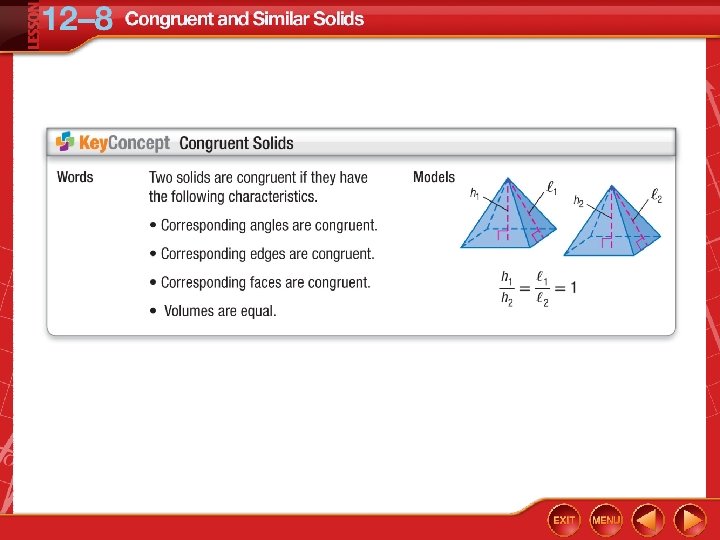
Identify Similar and Congruent Solids A. Determine whether the pair of solids is similar, congruent, or neither. If the solids are similar, state the scale factor. Find the ratios between the corresponding parts of the square pyramids. Substitution Simplify.

Identify Similar and Congruent Solids Substitution Simplify. Answer: The ratios of the measures are equal, so we can conclude that the pyramids are similar. Since the scale factor is not 1, the solids are not congruent.

Identify Similar and Congruent Solids B. Determine whether the pair of solids is similar, congruent, or neither. If the solids are similar, state the scale factor. Compare the ratios between the corresponding parts of the cones.

Identify Similar and Congruent Solids Substitution Simplify. Substitution Answer: Since the ratios are not the same, the cones are neither similar nor congruent.

A. Determine whether the pair of solids is similar, congruent, or neither. A. similar B. congruent C. neither

B. Determine whether the pair of solids is similar, congruent, or neither. A. similar B. congruent C. neither

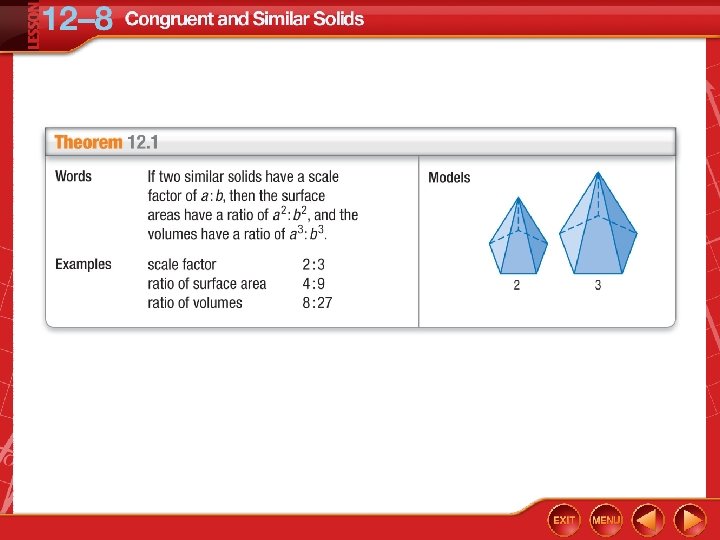
Use Similar Solids to Write Ratios Two similar cones have radii of 9 inches and 12 inches. What is the ratio of the volume of the smaller cone to the volume of the larger cone? First, find the scale factor. Write a ratio comparing the radii.

Use Similar Solids to Write Ratios If the scale factor is , then the ratio of the volumes is Answer: So, the ratio of the volume is 27: 64. .

Two similar cones have radii of 5 inches and 15 inches. What is the ratio of the volume of the smaller cone to the volume of the larger cone? A. 1: 3 B. 1: 9 C. 1: 27 D. 1: 81

Use Similar Solids to Find Unknown Values SOFTBALLS The softballs shown are similar spheres. Find the radius of the smaller softball if the radius of the larger one is about 1. 9 cubic inches. Analyze You know the volume of the softballs. Formulate Use Theorem 12. 1 to write a ratio comparing the volumes. Then find the scale factor and use it to find r.

Use Similar Solids to Find Unknown Values Determine Write a ratio comparing volumes. = Simplify. ≈ Write as .

Use Similar Solids to Find Unknown Values Ratio of radii Scale factor Find the cross products. r ≈ 1. 45 Solve for r. Answer: So, the radius of the smaller softball is about 1. 45 inches.

Use Similar Solids to Find Unknown Values Justify Evaluate For the two spheres to be similar, all corresponding measurements must have the same scale factor.

CONTAINERS The containers below are similar cylinders. Find the height h of the smaller container. A. 2 in. B. 3 in. C. 4 in. D. 5 in.

LESSON 12– 8 Congruent and Similar Solids