Lesson 10 Relation between two RVs produced in

Lesson 10 Relation between two RVs produced in the same experiment

Portfolio construction • We want to spend our money into several securities bought in the market. • So we need to study several securities (and therefore RV) together. • If securities were independent (on a market, think of the NYSE, and the dollar) it would be easy to build a portfolio with high return and zero risk.

One RV • • Collection of possible values (ai’s) Set of probabilities A long series of outcomes A histogram • The outcomes were produced by replication of an experiment E • In finance, the usual experiment is « wait one year » • Two concepts : the mean and the variance

Two RVs (produced in the same experiment) • All the initial concepts are naturally extended. • But there will also be a new one. • Old ones : – The set of possible values : a collection of pairs (ai, bj)’s – A set of probabilities : each pair has a probability – A long series of outcomes ; we can plot them and construct the extension of a histogram : a scattergram, and we count pairs that fell in each cell of a grid

2 RVs : the new concept • The new concept is : the variables may or may not be related – Some joint distributions (i. e. the set of probabilities) show independence, and some set of probabilities reveal dependence. – This can also be seen with scattergrams drawn from long series of actual outcomes of pairs. • Concept introduced by Karl Pearson (working with Francis Galton, a cousin of Charles Darwin) in the second half of the XIXth century, while studying the role of genetics in evolution and related topics in biology and agriculture.

Visual interpretation • The best way to « feel » the relationship between two RV is to look at their scattergram (or their joint distribution) • We « fit » an oval shape (with the appropriate technique which we won’t study) through the scattergram • The most important fact is whethere is an angle between the axes of the oval and the x and y axes • If the angle is zero : no relationship between X and Y. • If there is an angle : there is a relationship • The narrowness of the oval is related the strength of the relationship.

Negatively related RVs

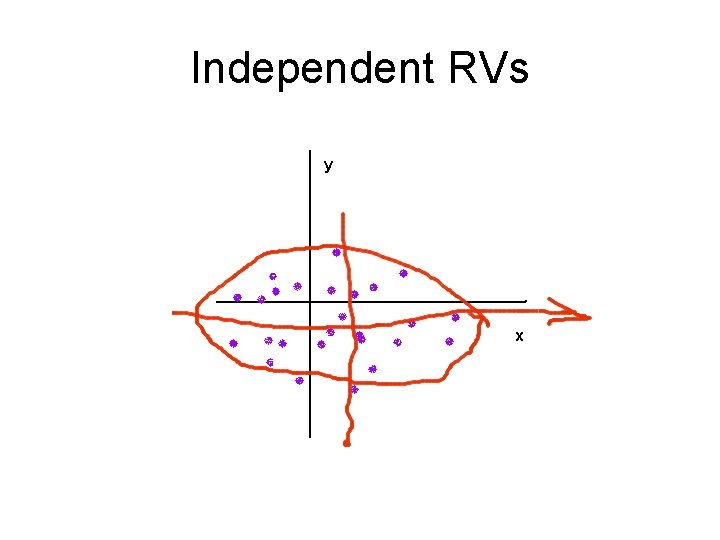
Independent RVs

The mathematical concept of covariance • Covariance is the formalisation of the relationship between 2 RVs • Correlation is a slight variation on covariance

Computation of covariance • If we remember how we computed the variance of one RV… • …then we extend this to 2 RVs.