LESSON 10 4 Mathematical Induction FiveMinute Check over

LESSON 10– 4 Mathematical Induction

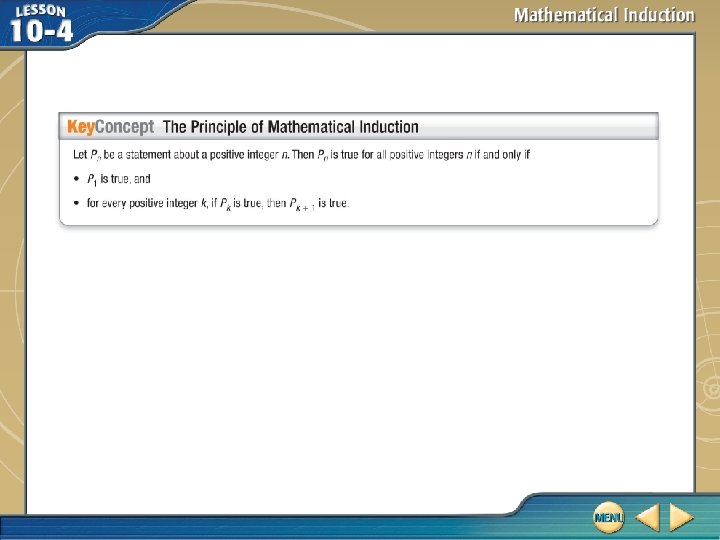
Five-Minute Check (over Lesson 10 -3) Then/Now New Vocabulary Key Concept: The Principle of Mathematical Induction Example 1: Prove a Summation Formula Example 2: Prove Divisibility Example 3: Prove Statements of Inequality Example 4: Use Extended Mathematical Induction Example 5: Real-World Example: Apply Extended Mathematical Induction

Over Lesson 10 -3 Determine the common ratio and find the next three terms of the geometric sequence A. B. C. D.

Over Lesson 10 -3 Write an explicit formula and a recursive formula for finding the nth term of the geometric sequence A. B. C. D.

Over Lesson 10 -3 Find the 14 th term of the geometric sequence 3, – 9, 27, …. A. a 14 = – 4, 782, 969 B. a 14 = 1, 594, 323 C. a 14 = 4, 782, 969 D. a 14 = 14, 348, 907

Over Lesson 10 -3 Find A. 1. 2 B. 2. 0 C. 3. 6 D. 6. 0 to the nearest tenth.

Over Lesson 10 -3 If possible, find the sum of the infinite geometric sequence 14, 7, 3. 5, 1. 75, …. A. 26. 25 B. 27 C. 28 D. not possible

You found the next term in a sequence or series. (Lesson 10 -1) • Use mathematical induction to prove summation formulas and properties of divisibility involving a positive integer n. • Use extended mathematical induction.

• principle of mathematical induction • anchor step • inductive hypothesis • inductive step • extended principle of mathematical induction

Prove a Summation Formula Use mathematical induction to prove that is true for all positive integers n. Conjecture Let Pn be the statement.

Prove a Summation Formula Anchor Step Verify that Pn is true for n = 1. P n: Original statement Pn. P 1: Pn for n = 1, the first partial sum Because is a true statement, Pn is true for n = 1.

Prove a Summation Formula Inductive Hypothesis Assume that Pn is true for n = k. To write the inductive hypothesis, replace n with k in Pn. That is, assume that P k: is true for some integer k. Inductive Step Use the inductive hypothesis to prove that Pn is true for n = k + 1. To prove that Pn is true for n = k + 1, we need to show that Pk + 1 is true. Start with your inductive hypothesis and then add the (k + 1)th term to each side.

Prove a Summation Formula Inductive hypothesis Add the (k + 1)th term to each side. Simplify the right-hand side.

Prove a Summation Formula Add fractions. Simplify the numerator. Factor 2 k 2 + 3 k + 1. Divide out common factor.

Prove a Summation Formula Rewrite denominator in terms of k + 1. This final statement, is exactly the statement for Pk + 1, so Pk + 1 is true. It follows that if Pn is true for n = k, then Pn is also true for n = k + 1.

Prove a Summation Formula Conclusion Because Pn is true for n = 1 and Pk implies Pk + 1, Pn is true for n = 2, n = 3, and so on. That is, by the principle of mathematical induction, P n: is true for all positive integers n.

Which of the following corresponds to the inductive hypothesis in mathematical induction to prove that 1 + 3 + 5 + … + 2 n – 1 = n 2 is true for all positive integers n? A. 2(1) – 1 = 12 B. Let Pn be the statement 1 + 3 + 5 + … + 2 n – 1 = n 2 is true for all positive integers n. C. Let Pk be the statement 1 + 3 + 5 + … + 2 k – 1 = k 2 is true for all positive integers k. D. Because Pn is valid for n = 1 and for n = k + 1, 1 + 3 + 5 + … + 2 n – 1 = n 2 is valid for all positive integers n.

Prove Divisibility Prove that 6 n – 1 is divisible by 5 for all positive integers n. Conjecture and Anchor Step Let Pn be the statement that 6 n – 1 is divisible by 5. P 1 is the statement that 61 – 1 is divisible by 5. P 1 is true, since 61 – 1 is 5, which is divisible by 5. Inductive Hypothesis and Step Assume that 6 k – 1 is divisible by 5, or 6 k – 1 = 5 r for some integer r. Use this hypothesis to show that 6 k + 1 – 1 is divisible by 5.

Prove Divisibility 6 k – 1 = 5 r Inductive hypothesis 6(6 k – 1) = 6(5 r) Multiply each side by 6. 6 k + 1 – 6 = 30 r Simplify. 6 k + 1 – 1 = 30 r + 5 Add 5 to each side. 6 k + 1 – 1 = 5(6 r + 1) Factor. Because r is an integer, 6 r + 1 is an integer and 5(6 r + 1) is divisible by 5. Therefore, 6 k + 1 – 1 is divisible by 5.

Prove Divisibility Conclusion Because Pn is valid for n = 1 and Pk implies Pk + 1, Pn is true for n = 2, n = 3, and so on. By the principle of mathematical induction, 6 n – 1 is divisible by 5 for all positive integers n.

Which of the following corresponds to the conclusion in mathematical induction to prove 3 n – 1 is divisible by 2 for all positive intengers n? A. 31 – 1 is divisible by 2 B. Because Pn is true for n = 1 and Pk implies Pk + 1, Pn is true for n = 2, n = 3, and so on. By the principle of mathematical induction, 3 n – 1 is divisible by 2 for all positive integers n. C. Let Pn be the statement that 3 n – 1 is divisible by 2. D. Assume that 3 k – 1 is divisible by 2.

Prove Statements of Inequality Prove that 3 n < 4 n for all positive integers n. Conjecture and Anchor Step Let Pn be the statement 3 n < 4 n. P 1 and P 2 are true, since 3(1) < 41 and 3(2) < 42 are true inequalities. Showing P 2 to be true provides the anchor for the second part of the inductive hypothesis below. Inductive Hypothesis and Step Assume that 3 k < 4 k is true for a positive integer k > 1. Use both parts of this hypothesis to show that 3(k + 1) < 4 k + 1 is true. Start with the first part of the hypothesis.

Prove Statements of Inequality 3 k < 4 k Inductive hypothesis 4 • 3 k < 4 • 4 k 12 k < 4 k + 1 Multiply each side by 4. Simplify each side. Now use the second part of the hypothesis. k >1 k– 1 >0 3 k – 3 > 0 6 k – 3(k + 1) > 0 Inductive hypothesis Subtract 1 from each side. Multiply each side by 3. 3 k = 6 k – 3 k Factor.

Prove Statements of Inequality 6 k > 3(k + 1) Add 3(k + 1) to each side. 3(k + 1) < 6 k If a > b, then b < a. Since k is a positive integer, 6 k < 12 k. By the Transitive Property of Inequality, if 3(k + 1) < 6 k and 6 k < 12 k, then 3(k + 1) < 12 k. By this same property, if 3(k + 1) < 12 k and 12 k < 4 k + 1, then 3(k + 1) < 4 k + 1. Conclusion Since Pn is true for n = 1, n = 2, and Pk implies Pk + 1 for k > 1, Pn is true for n = 3, n = 4, and so on. By the principle of mathematical induction, 3 n < 4 n is true for all positive integers n.

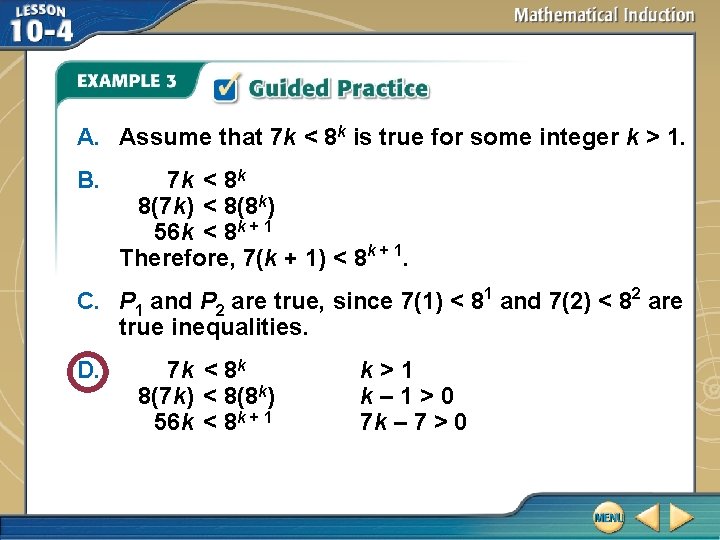
Which of the following corresponds to the inductive step in mathematical induction to prove 7 n < 8 n for all positive integers n?

A. Assume that 7 k < 8 k is true for some integer k > 1. B. 7 k < 8 k 8(7 k) < 8(8 k) 56 k < 8 k + 1 Therefore, 7(k + 1) < 8 k + 1. C. P 1 and P 2 are true, since 7(1) < 81 and 7(2) < 82 are true inequalities. D. 7 k < 8 k 8(7 k) < 8(8 k) 56 k < 8 k + 1 k>1 k– 1>0 7 k – 7 > 0

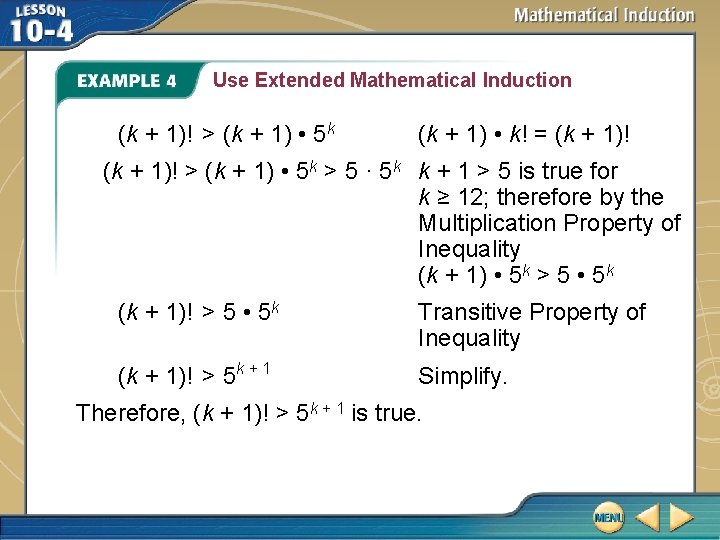
Use Extended Mathematical Induction Prove that n! > 5 n for integer values of n ≥ 12. Conjecture and Anchor Step Let Pn be the statement n! > 5 n. P 12 is true since 12! > 512 or 479, 001, 600 > 244, 140, 625 is a true statement. Inductive Hypothesis and Step Assume that k! > 5 k is true for a positive integer k ≥ 12. Show that (k + 1)! > 5 k + 1 is true. k! > 5 k Inductive hypothesis (k + 1) • k! > (k + 1) • 5 k Multiply each side by k+1

Use Extended Mathematical Induction (k + 1)! > (k + 1) • 5 k (k + 1) • k! = (k + 1)! > (k + 1) • 5 k > 5 · 5 k k + 1 > 5 is true for k ≥ 12; therefore by the Multiplication Property of Inequality (k + 1) • 5 k > 5 • 5 k (k + 1)! > 5 • 5 k Transitive Property of Inequality (k + 1)! > 5 k + 1 Simplify. Therefore, (k + 1)! > 5 k + 1 is true.

Use Extended Mathematical Induction Conclusion Because Pn is true for n = 12 and Pk implies Pk + 1 for k ≥ 12 , Pn is true for n = 13, n = 14, and so on. That is, by the extended principle of mathematical induction, n! > 5 n is true for all integer values of n ≥ 12.

For which of the following statements would you apply the extended principle of mathematical induction in the proof? A. 3 + 6 + 9 + … + 3 n = integers. for all positive B. n 2 < 5 n for n ≥ 3. C. 2 + 6 + 18 + … + 2 • 3 n – 1 = 3 n – 1 for n ≥ 1. D. n 2 < 3 n for n ≥ 1.

Apply Extended Mathematical Induction READING Prove that all coupons earned in the reading program for free pizzas can be awarded as 2 -pizza and 5 -pizza coupons as long as the number of pizzas awarded is greater than 4. Conjecture and Anchor Step Let Pn be the statement that there exists a set of 2 -pizza vouchers and 5 -pizza vouchers that adds to n for n > 4. For n = 5, the conjecture is true, because 5 = 2(0) + 5(1).

Apply Extended Mathematical Induction Inductive Hypothesis and Step Assume that for n = k, there exists a set of 2 - and/or 5 -pizza vouchers that adds to k. Show that this implies the existence of a set of 2 - and/or 5 -pizza vouchers that adds to k + 1. Case 1: The set contains at least one 5 -pizza voucher. Replace one 5 -pizza voucher with three 2 -pizza vouchers and the set’s value is increased to k + 1, which is exactly Pk + 1.

Apply Extended Mathematical Induction Case 2: The set contains no 5 -pizza vouchers. The set must contain at least three 2 -pizza vouchers, because the set’s value must be greater than 4. Replace two of the 2 -pizza vouchers with a 5 -pizza voucher and the set’s value is increased to k + 1, which is exactly Pk + 1. Conclusion In both cases, Pn is true for n = k + 1. Because Pn is true for n = 5 and Pk implies Pk + 1 for n ≥ 5, Pn is true for n = 6, n = 7, and so on. That is, by the extended principle of mathematical induction, all pizza orders greater than 4 can be covered by 2 - and 5 -pizza vouchers.

ENTERTAINMENT The tickets to a musical sell for $35, $50, $90, and $130, and so on. Suppose you want to prove that all of the tickets over $40 can be paid for using just $20 bills and $50 bills. Which of the following is a valid conjecture? A. Let Pn be the set of $20 -bills and $50 -bills that adds to $10 n for n > 40. B. Let Pn be the set of $20 -bills and $50 -bills that adds to $10 + 40 n for n > 1. C. Let Pn be the set of $20 -bills and $50 -bills that adds to $10 + 5 n for n > 35. D. Let Pn be the set of $20 -bills and $50 -bills that adds to $40 n for n > 1.

LESSON 10– 4 Mathematical Induction