Lesson 10 2 Arcs and Chords Vocabulary Central

Lesson 10. 2: Arcs and Chords

Vocabulary • Central angle: an angle whose vertex is the center of the circle • Minor arc: formed by the interior of an angle • Major arc: the exterior portion of the angle • Measure of a minor arc: equal to the central angle • Measure of a major arc: 360 – minor arc.

Postulate • Arc Addition Postulate: The measure of an arc formed by two adjacent arcs is the sum of the measures of the two arcs S T V m. TS + m. SV = m. TV

Theorems • Thm 10. 4: In the same circle, or in congruent circles, two minor arcs are congruent iff their corresponding chords are congruent • Thm 10. 5: If the diameter of a circle is perpendicular to a chord, then the diameter bisects the chord and its arc.

Theorems • Thm 10. 6: If one chord is a perpendicular bisector of another chord, then the first chord is the diameter
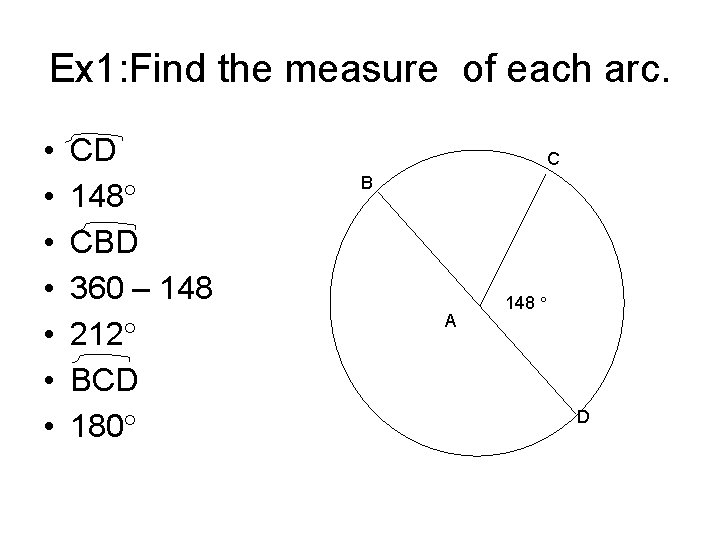
Ex 1: Find the measure of each arc. • • CD 148 CBD 360 – 148 212 BCD 180 C B A 148 D
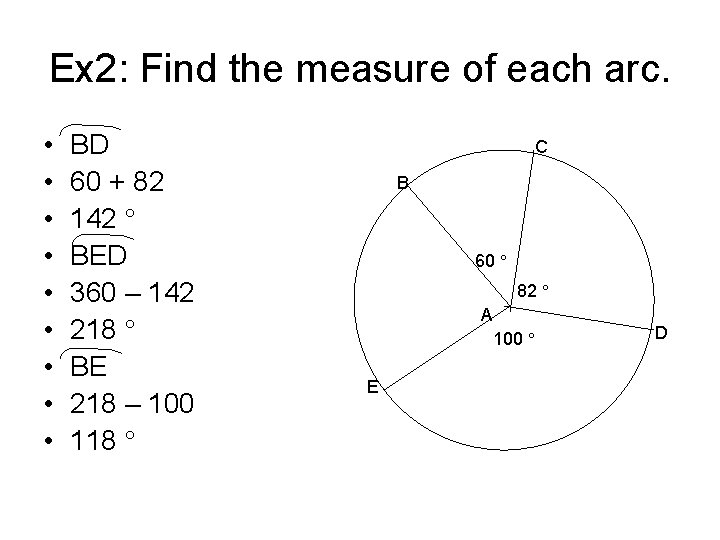
Ex 2: Find the measure of each arc. • • • BD 60 + 82 142 BED 360 – 142 218 BE 218 – 100 118 C B 60 82 A 100 E D
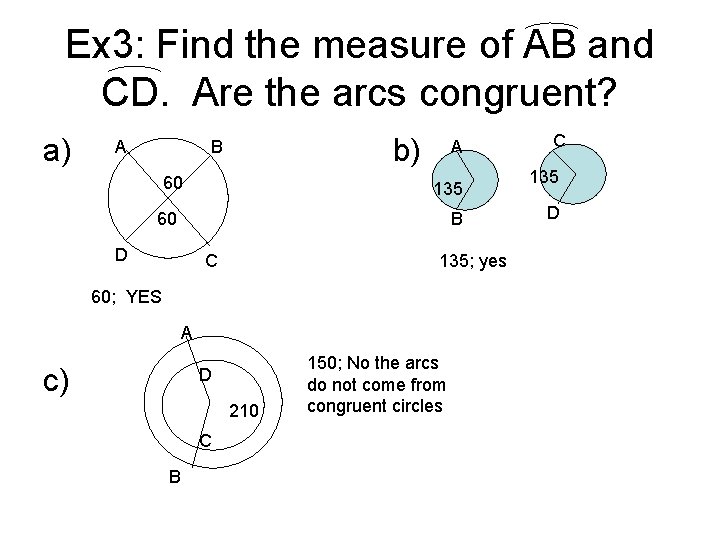
Ex 3: Find the measure of AB and CD. Are the arcs congruent? a) A b) B 60 A 135 60 B D C 135; yes 60; YES A c) D 210 C B 150; No the arcs do not come from congruent circles C 135 D
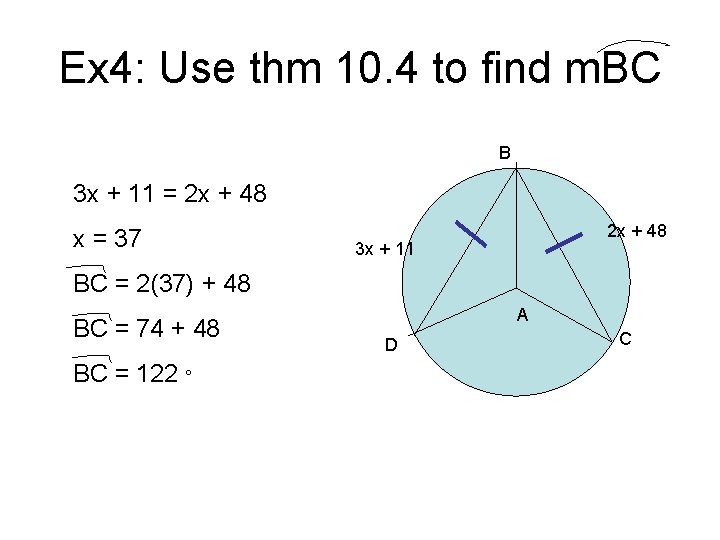
Ex 4: Use thm 10. 4 to find m. BC B 3 x + 11 = 2 x + 48 x = 37 2 x + 48 3 x + 11 BC = 2(37) + 48 BC = 74 + 48 BC = 122 A D C
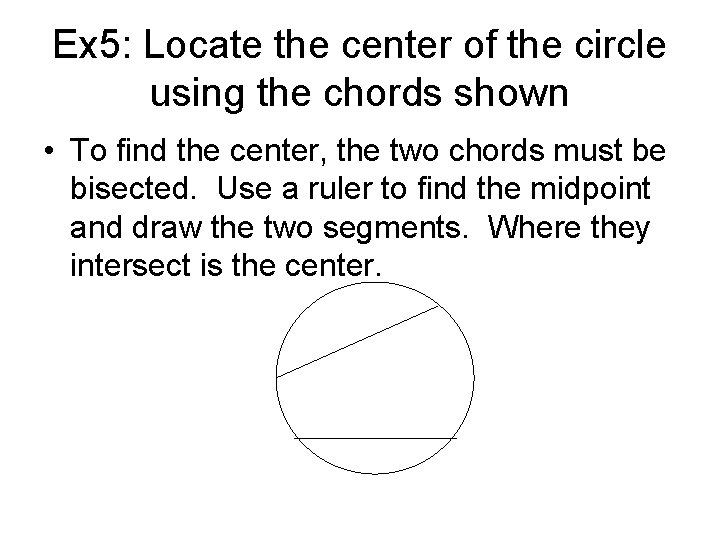
Ex 5: Locate the center of the circle using the chords shown • To find the center, the two chords must be bisected. Use a ruler to find the midpoint and draw the two segments. Where they intersect is the center.
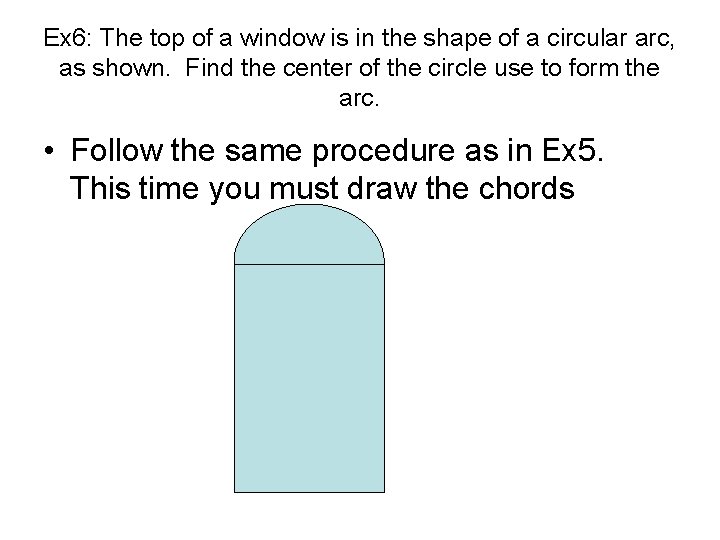
Ex 6: The top of a window is in the shape of a circular arc, as shown. Find the center of the circle use to form the arc. • Follow the same procedure as in Ex 5. This time you must draw the chords
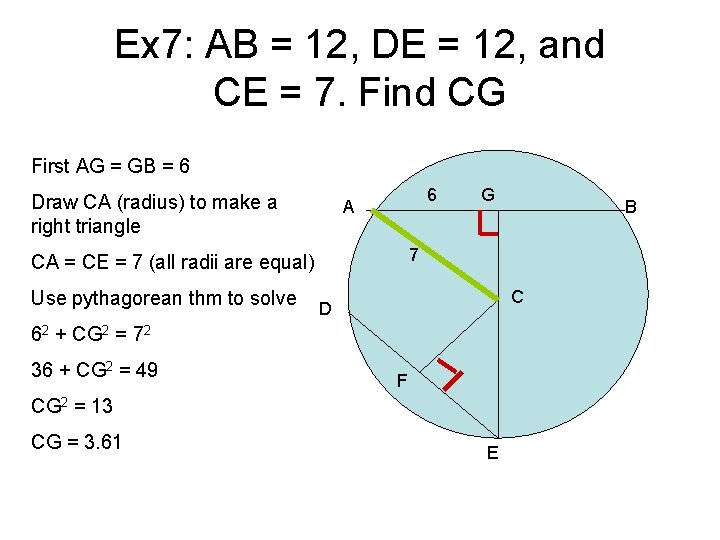
Ex 7: AB = 12, DE = 12, and CE = 7. Find CG First AG = GB = 6 Draw CA (radius) to make a right triangle 6 A C D 62 + CG 2 = 72 36 + CG 2 = 49 F CG 2 = 13 CG = 3. 61 B 7 CA = CE = 7 (all radii are equal) Use pythagorean thm to solve G E
- Slides: 12