LESSON 10 1 10 2 POLYHEDRONS OBJECTIVES To

LESSON 10. 1 & 10. 2 POLYHEDRONS OBJECTIVES: To define polyhedrons To recognize nets of space figures To apply Euler’s formula To describe cross section of 3 -D figures

A POLYHEDRON is a solid figure formed by flat surfaces enclosed by polygons.

PARTS OF A POLYHEDRON FACES the sides (flat surfaces) of a polyhedron EDGES the segment where two faces intersect. VERTEX the point where three or more faces intersect.

Rectangular prism Edge Face Vertex How many faces does this polyhedron have? Edges? Vertices? 6 12 8

Euler’s Formula: § Faces + Vertices = Edges + 2 § OR F+V=E+2

Polyhedrons are classified by the number of faces. # faces 4 tetrahedron 5 pentahedron 6 hexahedron 7 heptahedron

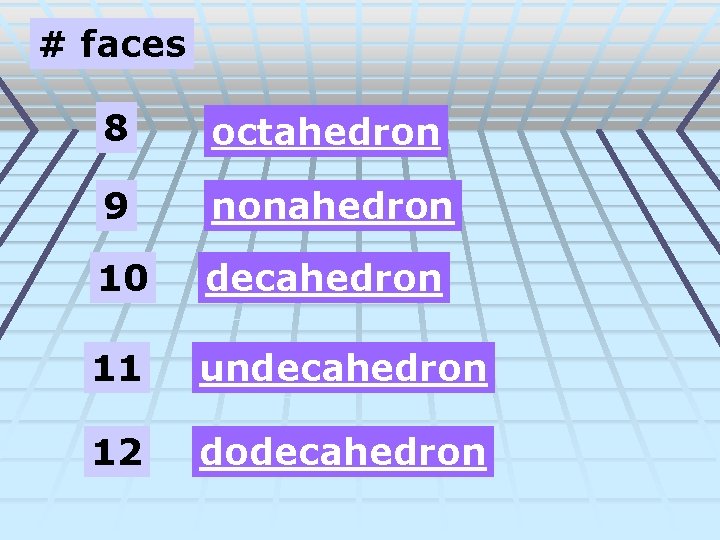
# faces 8 octahedron 9 nonahedron 10 decahedron 11 undecahedron 12 dodecahedron

A net is a two-dimensional pattern that can be folded to form a three-dimensional figure.

Examples Using Nets #1 Identifying a net Is the given pattern a net for a cube? If so, name two letters that will be opposite faces. A B C D E F

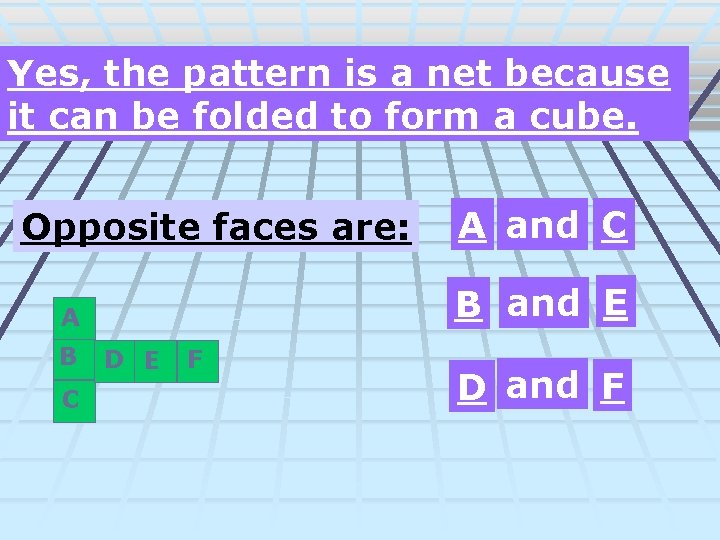
Yes, the pattern is a net because it can be folded to form a cube. Opposite faces are: B and E A B C A and C D E F D and F

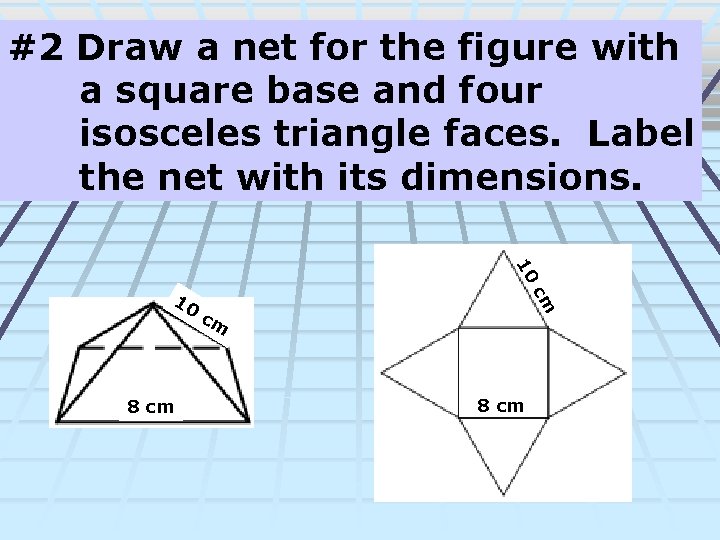
#2 Draw a net for the figure with a square base and four isosceles triangle faces. Label the net with its dimensions. 10 8 cm cm 10 cm 8 cm

#3 Use Euler’s Formula to find the number of vertices on a polyhedron with 8 triangular faces. Calculate edges first. 8 faces * 3 sides = 24 24/2 = 12 edges (we do not want duplicate edges) F+V=E+2 8 + V = 12 + 2 8 + V = 14 V=6

Lesson 10. 2 A cross section is the intersection of a solid and a plane. You can think of a cross section as a very thin slice of the solid.

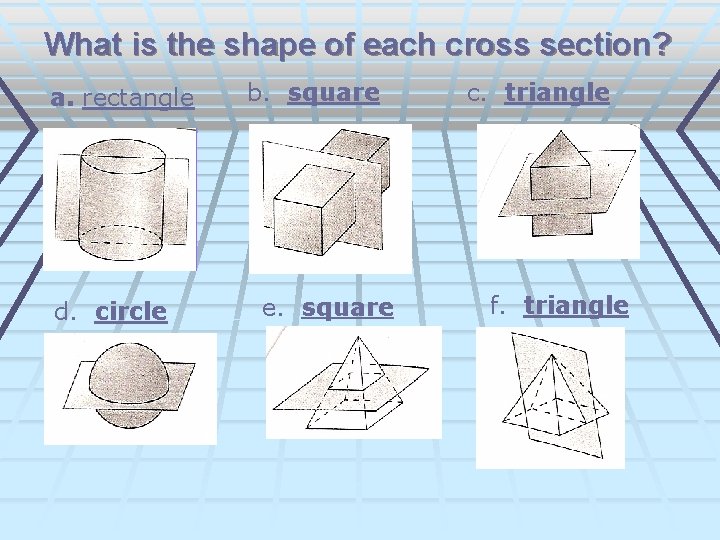
What is the shape of each cross section? a. rectangle d. circle b. square e. square c. triangle f. triangle

ASSIGNMENT Pg. 514 #1 -9, 13 -18, 20 -21, 29 a AND Pg. 524 #17 -19, 40 -42