Lesson 1 Solving Inequalities Using Addition and Subtraction

Lesson 1: Solving Inequalities Using Addition and Subtraction

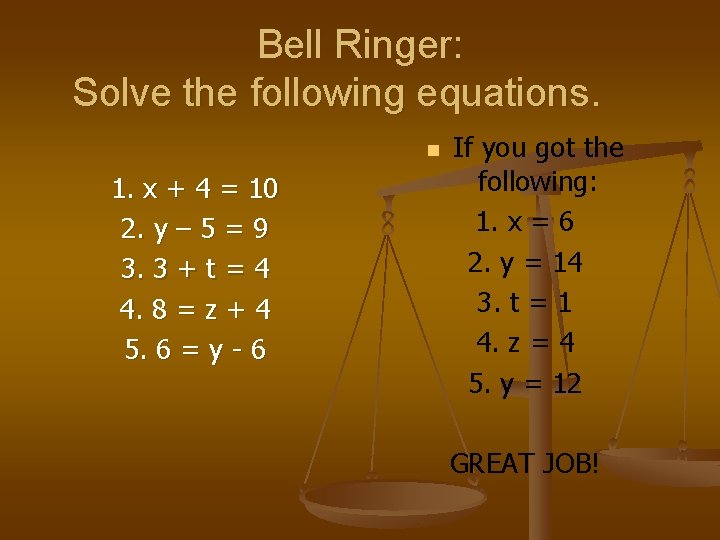
Bell Ringer: Solve the following equations. n 1. x + 4 = 10 2. y – 5 = 9 3. 3 + t = 4 4. 8 = z + 4 5. 6 = y - 6 If you got the following: 1. x = 6 2. y = 14 3. t = 1 4. z = 4 5. y = 12 GREAT JOB!

Show me how you got the bell ringer To solve the previous problems, you must treat the equation like a balance. To solve #1 for x, you must subtract 4 from both sides of the equation. LIKE THIS: x + 4 = 10 -4 -4 x=6 #2) y – 5 = 9. +5 +5 y = 14 #3) 3 + t = 4 -3 -3 t=1 #4) 8 = z + 4 -4 -4 4=z #5) 6 = y – 6 +6 +6 12 = y

Definition n Inequality : An inequality is a mathematical sentence that contains a symbol; greater than (>), less than (< ( ), less than or equal to greater than or equal to. n In which the terms on either side of the symbol are unequal (x < y, 7 > 3).

Solving Inequalities are no different than solving equations; like in the bell ringer. 1. Solve for x. x+5<11 -5 -5 (solve by subtraction) x<6 2. Solve for y. 2>y– 4 +4 +4 (solve by adding) 6>y

Some problem require you to write the inequality, then solve. Solve the following inequality; Five added to a number is at least eight. z +5 > 8 (choose any variable) -5 -5 z>3 *note: “at least” think of it’s meaning as z+5 is at least 8, which means it’s at smallest 8 but it could be larger. Therefore using the “greater than or equal” to symbol.

Try a few. 1. 2. 3. 4. 3>n– 2 z+3<5 4 less than a number is no more than 5. The sum of a number and 4 is less than 6. 1. 2. 3. 4. 6>n Z<2 (n - 4 < 5) n <9 (n+4 <6) n<2