LESSON 1 7 THE DISTRIBUTIVE PROPERTY The distributive

LESSON 1 -7 THE DISTRIBUTIVE PROPERTY
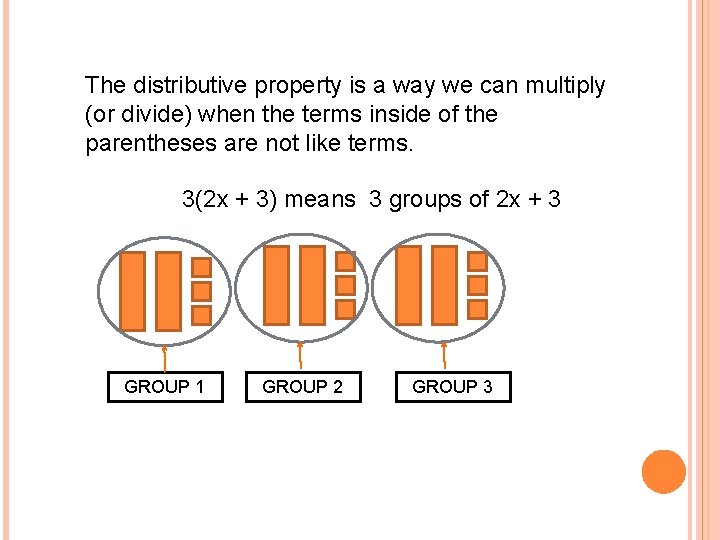
The distributive property is a way we can multiply (or divide) when the terms inside of the parentheses are not like terms. 3(2 x + 3) means 3 groups of 2 x + 3 GROUP 1 GROUP 2 GROUP 3
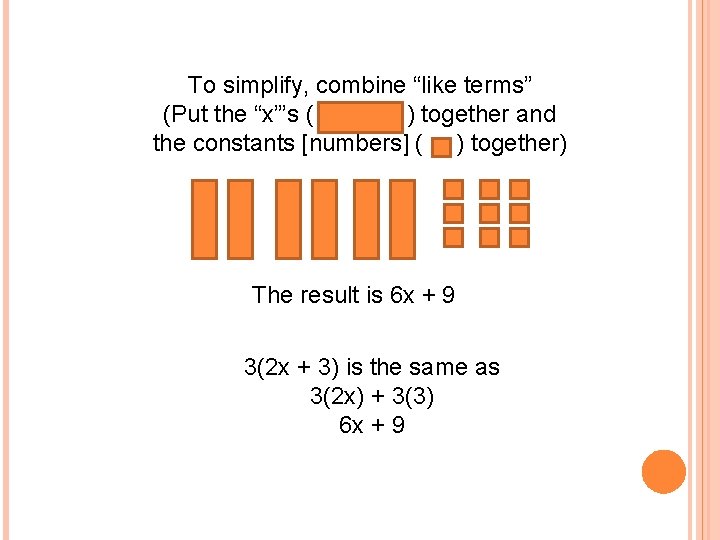
To simplify, combine “like terms” (Put the “x”’s ( ) together and the constants [numbers] ( ) together) The result is 6 x + 9 3(2 x + 3) is the same as 3(2 x) + 3(3) 6 x + 9

To work a problem that involves the distributive property, multiply the value outside of the parentheses times each item inside of the parentheses. (It may be helpful to rewrite everything in the parentheses so that it is an addition problem if there is subtraction involved. ) For example, -3(x – 2) would be rewritten as -3(x + – 2 ). After multiplying, combine like terms.

Simplify each expression using the distributive property 3(x) + 3(8) A. 3(x + 8) = _________ 3 x + 24 _________ (5 b + – 4) (– 7) B. (5 b – 4)(– 7) = – – – (5 b) ( 7) + ( 4)( 7) _________ Use subtraction – 35 b + 28 rules to rewrite _________ problem. _________
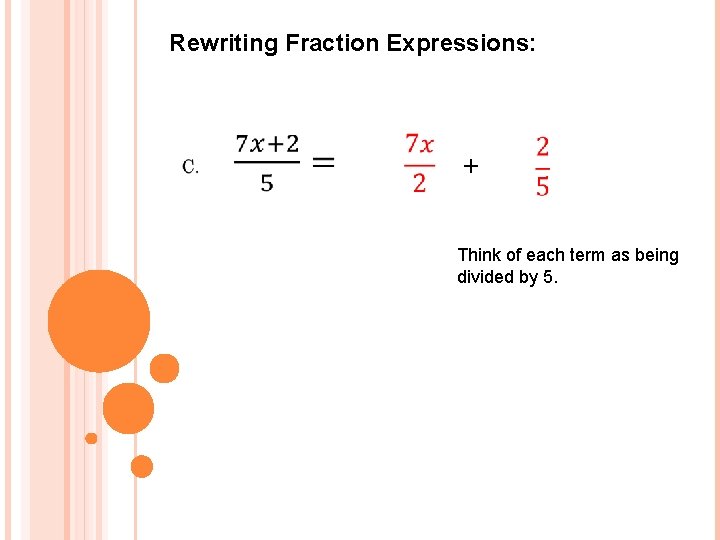
Rewriting Fraction Expressions: + Think of each term as being divided by 5.
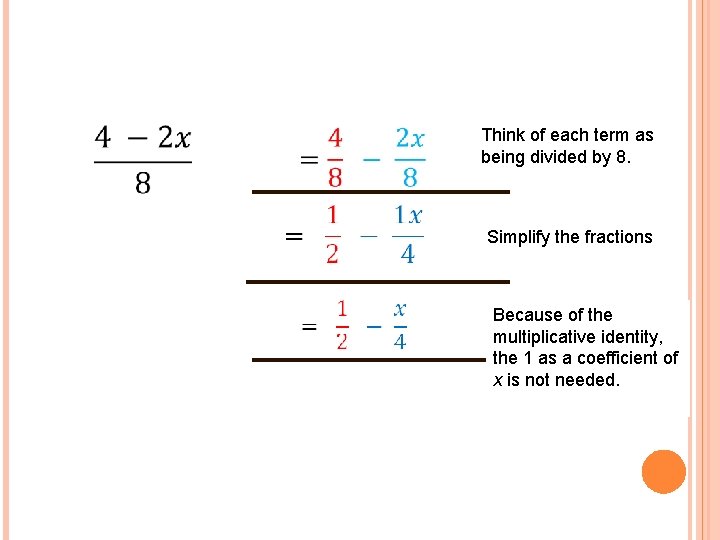
Think of each term as being divided by 8. Simplify the fractions Because of the multiplicative identity, the 1 as a coefficient of x is not needed.

USING THE MULTIPLICATION PROPERTY OF – 1 (REMEMBER – 1 ● X = –X ) – 1(2 y – 3 x) + – (2 y – 3 x) = _________ There is an understood “ 1” with the “–” sign. – 1(2 y) + – 1(– 3 x) = ___________ – 2 y + 3 x = ___________ OR 3 x – 2 y = ___________
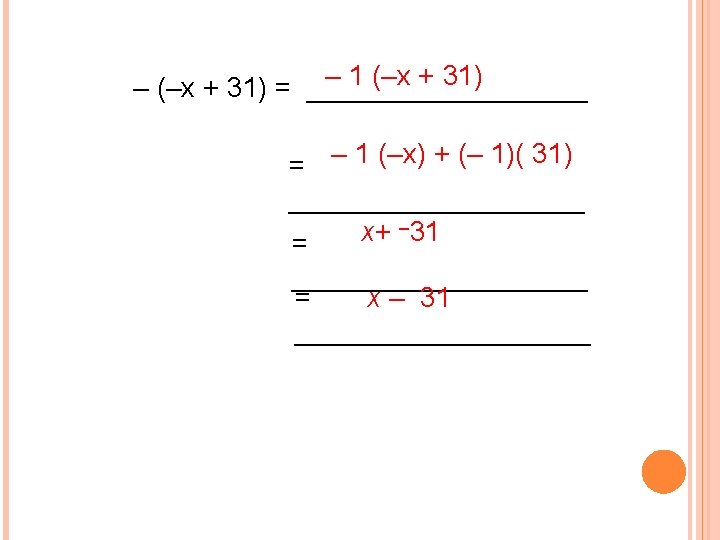

term In an algebraic expression, a _____ is a number, a variable, or the product of a number and constant one or more variables. A ________ is a coefficient term that has no variable. A ________ is a numerical factor of a term. Like terms ___________ have the same variable factors (raised to the same power).

Like Terms? Why or why not? Yes, they both have the variable “a” 7 a & – 3 a ___________ 4 x 2 & Yes, they both have the variable “x 2” 2 12 x __________ No, the second term does not have a “b” 6 ab & – 2 a __________ xy 2 & x 2 y No, the 1 st term has “y 2” and the 2 nd term has “x 2” ___________

COMBINING LIKE TERMS: 8 x 2 + It’s okay to just add the (8 + 2) coefficients of the like terms. 2 x 2 = _________ (x 2) 10 x = _________ 2 Change subtraction to addition – 3 + – 3 x + 6 y + 4 5 x + 5 x – 3 x + 6 y + 4 = __________ (5 x + – 3 x) + 6 y + (4+ – 3) = _____________ Group like terms together 2 x + 6 y + 1 Simplify = _____________


For a video explanation go to: Pearson Success Net Virtual Nerd for Lesson 1 -7 You may have to be logged in to your Pearson (textbook) account to view this, but try anyway.
- Slides: 15