Lesson 1 6 Solving Quadratic Equations Objective Objective

Lesson 1 -6 Solving Quadratic Equations

Objective:

Objective: • To solve quadratic equations using different methods.

Quadratic Equation:

Quadratic Equation: • Any equation that can be written in ax 2 + bx + c = 0 form.

Three methods for solving quadratic equations:

Three methods for solving quadratic equations: 1) Factoring.

Three methods for solving quadratic equations: 1) Factoring. 2) Completing the square.

Three methods for solving quadratic equations: 1) Factoring. 2) Completing the square. 3) Quadratic formula.

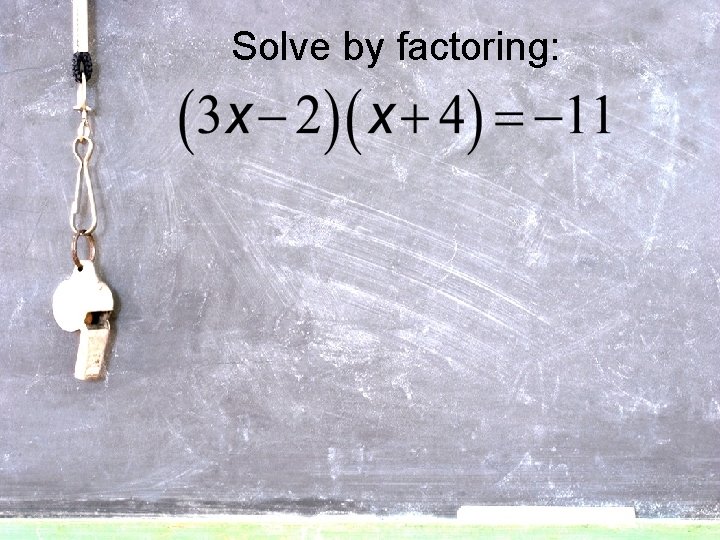
Solve by factoring:

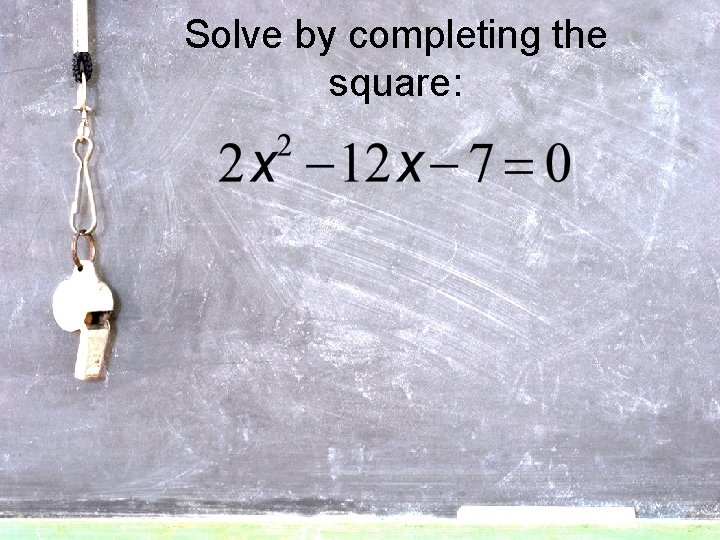
Solve by completing the square:

Solve by using the Quadratic Formula:

Quadratic Formula:

Quadratic Formula: • The discriminant is the expression which is under the radical.

Quadratic Formula: • The discriminant is the expression which is under the radical. • The discriminant tells us something special about the roots (xintercepts) and the solutions (roots and zeros).

Quadratic Formula:

Quadratic Formula: • If there will exist 2 complex conjugate roots.

Quadratic Formula: • If there will exist 2 complex conjugate roots. • If there will exist 1 real root called a double root.

Quadratic Formula: • If there will exist 2 complex conjugate roots. • If there will exist 1 real root called a double root. • If there will exist 2 distinct real roots.

Helpful Hints when Solving Equations:

Helpful Hints when Solving Equations: • If a, b, and c are integers, and if b 2 - 4 ac is a perfect square, then factor.

Helpful Hints when Solving Equations: • If the equation has the form x 2 + (even #)x + constant = 0, then solve by completing the square.

Helpful Hints when Solving Equations: • If neither of those two cases work, then use the quadratic formula.

Two Special Circumstances to Look For:

Two Special Circumstances to Look For: • Losing a Root

Two Special Circumstances to Look For: • Losing a Root • Gaining a Root

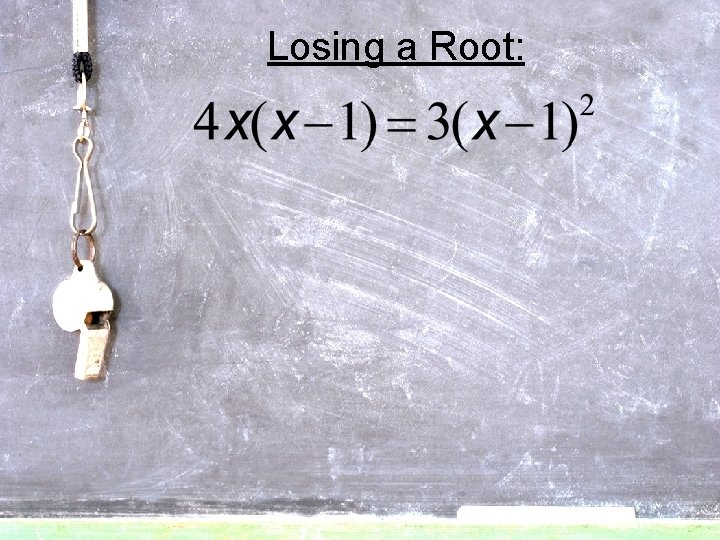
Losing a Root:

Gaining a Root: (Check for Extraneous Roots)

Assignment: Pgs. 34 -35 C. E. 1 -19 all, W. E. 1 -19 odd