Lesson 1 6 Core Focus on Geometry Congruent

Lesson 1. 6 Core Focus on Geometry Congruent and Similar Triangles

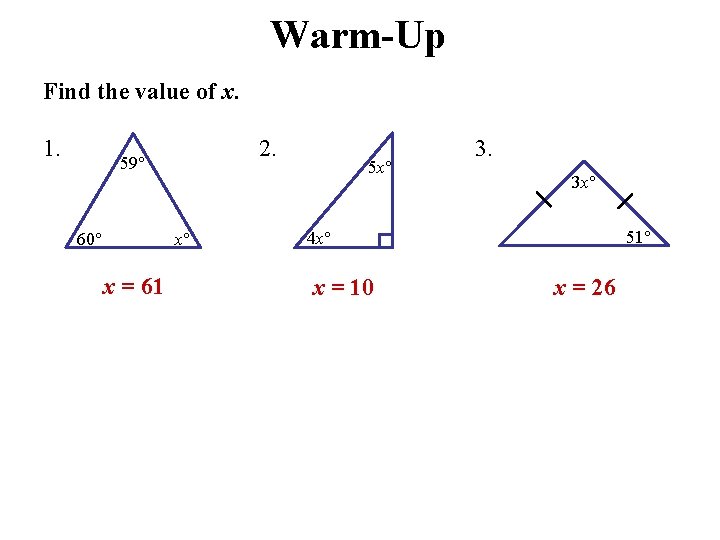
Warm-Up Find the value of x. 1. 2. 59 60 x x = 61 5 x 3. 3 x 51 4 x x = 10 x = 26

Lesson 1. 6 Congruent and Similar Triangles Determine if triangles are similar or congruent and find missing measures.

Vocabulary Congruent Figures Two figures that are the exact same shape and the exact same size. Similar Figures Two figures that have the exact same shape but not necessarily the same size. Corresponding Parts The angles and sides in similar or congruent figures that match.

Congruent and Similar Triangles Congruent Triangles All corresponding angles are congruent and all corresponding sides are congruent. Similar Triangles All corresponding angles are congruent and all corresponding sides are proportional.

Example 1 ΔMNP is similar to ΔJKL. Find the value of x, y and z. Since the triangles are similar, the corresponding angles are congruent. The sides of the congruent triangles are proportional. Substitute the values of each known side into the proportion. m L = m P m L = x = 50

Example 1 Continued… ΔMNP is similar to ΔJKL. Find the value of x, y and z. Set the cross products equal to each other. Divide both sides of the equation by 8. To find the value of z, set the sum of the three angles in the triangle equal to 180. 8 y = 120 8 8 y = 15 z + 50 + 90 = 180 z + 140 = 180 – 140 Subtract 140 from both sides of the equation. z = 40

Good to Know! If two angles in one triangle are congruent to two angles in another triangle, then the two triangles are similar. This rule is referred to as the Angle-Angle Similarity Theorem. When two corresponding angles in a pair of triangles are congruent, their sides are proportional. The triangles shown above are similar because A P and N I. The Angle-Angle Similarity Theorem can be illustrated by showing that if two pairs of corresponding angles are congruent in the triangles, the third pair of corresponding angles are also congruent. P + I + G = 180 A + N + T = 180 27 + 131 + G = 180 27 + 131 + T = 180 G = 22 a T = 22 a So, when two angles in two different triangles are equal, the third angles will also be congruent.

Angle-Angle Similarity Rule If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar.

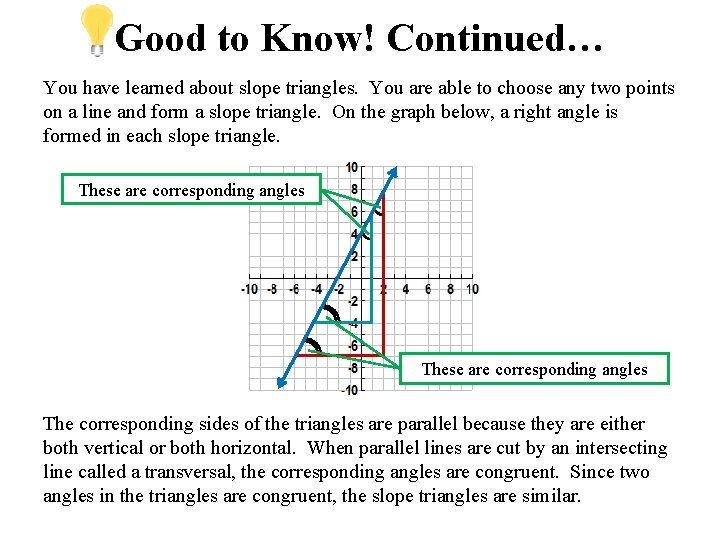
Good to Know! Continued… You have learned about slope triangles. You are able to choose any two points on a line and form a slope triangle. On the graph below, a right angle is formed in each slope triangle. These are corresponding angles The corresponding sides of the triangles are parallel because they are either both vertical or both horizontal. When parallel lines are cut by an intersecting line called a transversal, the corresponding angles are congruent. Since two angles in the triangles are congruent, the slope triangles are similar.

Communication Prompt Are congruent triangles similar? Explain.

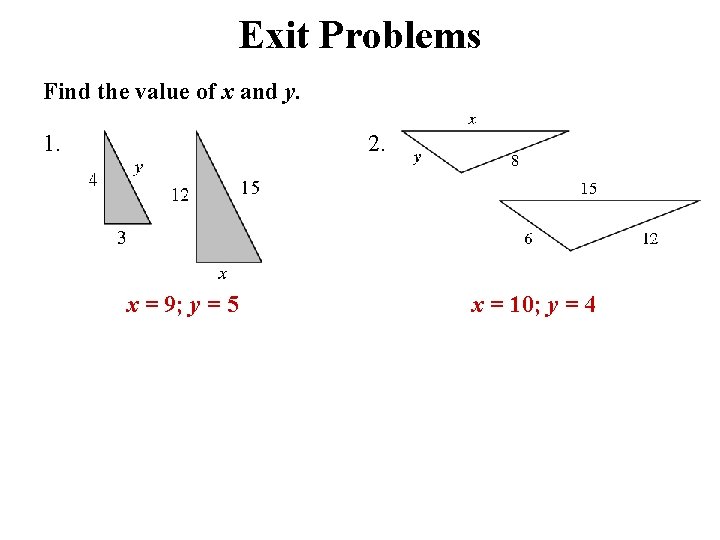
Exit Problems Find the value of x and y. 1. 2. x = 9; y = 5 x = 10; y = 4