Lesson 1 6 Core Focus on Functions Data

Lesson 1. 6 Core Focus on Functions & Data Stretching and Shrinking Functions

Warm-Up Describe the transformation that occurs to f(x). 1. −f (x) Reflection over x-axis 3. f (–x) Reflection over the y-axis 2. f (x − 1) + 3 Right 1 unit, up 3 units 4. f (x + 4) − 10 Left 4 units, down 10 units

Lesson 1. 6 Stretching and Shrinking Functions Stretch and shrink graphs and write equations to represent the changes in the graphs.

Explore! Stretch and Shrink When stretching or shrinking a function vertically, the x-values in the function do not change. Step 1 Copy and complete the table of values for the function f (x) = x². Step 2 Graph the function and connect the points with a smooth curve. Step 3 Copy and complete the table of values for the function g(x) = 2 x². Graph this function on the same coordinate plane as f (x). Step 4 How do the two graphs compare? Do you think f (x) was stretched or shrunk to form g(x)? Step 5 Copy and complete the table of values for the function h(x) = x ². Graph this function on the same coordinate plane as f (x) and g(x).

Explore! Stretch and Shrink Step 6 How do the original graph, f (x), and h(x) compare? Do you think f (x) was stretched or shrunk to form h(x)? Step 7 You have graphed f (x) after it was multiplied by factors of 3 and. One factor stretched the graph of f (x) and the other factor shrunk the graph. Use your graphing calculator to graph different factors as coefficients of x 2 with the parent function f (x). What type of numbers cause a graph to be stretched vertically? Shrunk vertically? Step 8 Did you try any factors that were negative numbers? If not, try at least two different negative factors as a coefficient of x 2. What do you notice about the graphs of these functions? How do they relate to f (x)? How does this connect to your previous learning? Step 9 Summarize your findings by completing the sentences: • A graph is stretched vertically when the function is multiplied by a factor… • A graph is shrunk vertically when the function is multiplied by a factor…

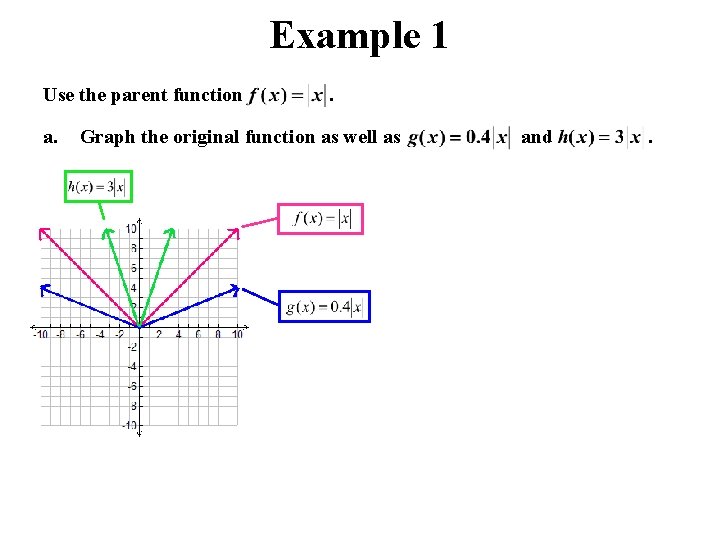
Example 1 Use the parent function a. . Graph the original function as well as and .

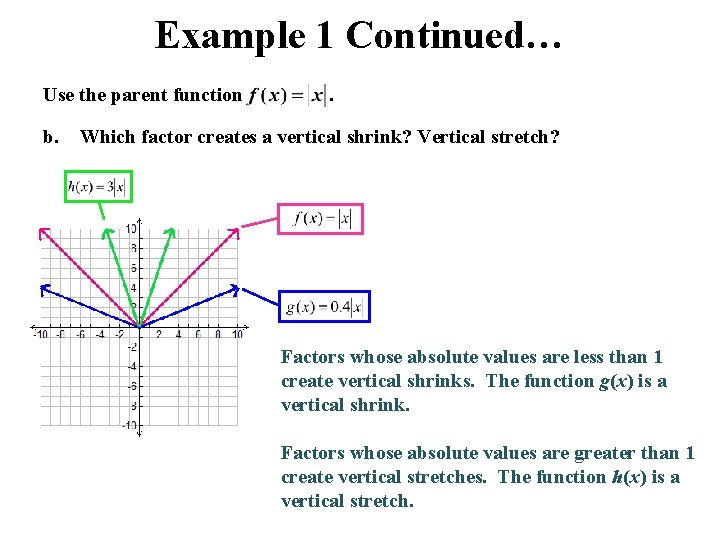
Example 1 Continued… Use the parent function b. . Which factor creates a vertical shrink? Vertical stretch? Factors whose absolute values are less than 1 create vertical shrinks. The function g(x) is a vertical shrink. Factors whose absolute values are greater than 1 create vertical stretches. The function h(x) is a vertical stretch.

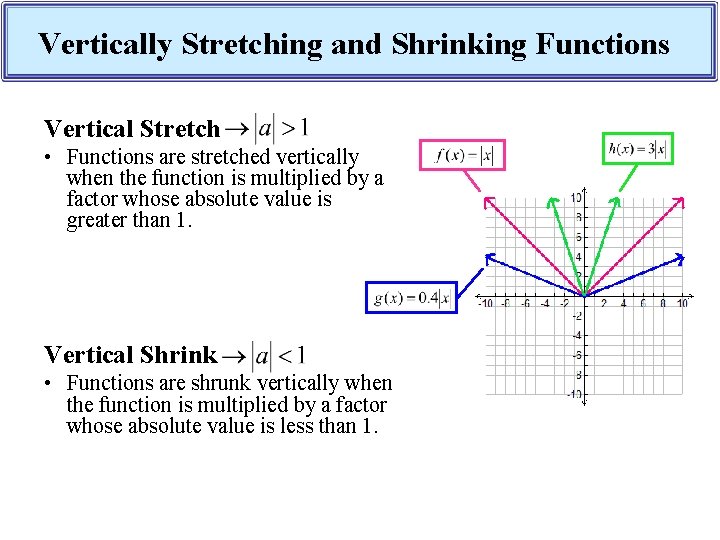
Vertically Stretching and Shrinking Functions Vertical Stretch • Functions are stretched vertically when the function is multiplied by a factor whose absolute value is greater than 1. Vertical Shrink • Functions are shrunk vertically when the function is multiplied by a factor whose absolute value is less than 1.

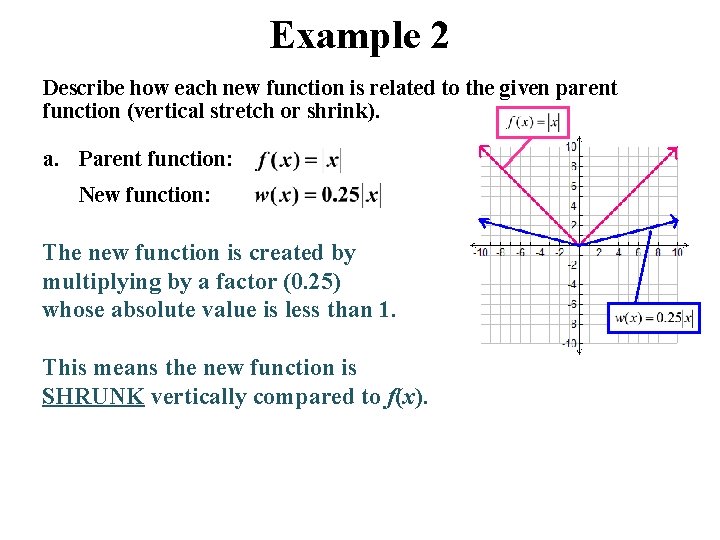
Example 2 Describe how each new function is related to the given parent function (vertical stretch or shrink). a. Parent function: New function: The new function is created by multiplying by a factor (0. 25) whose absolute value is less than 1. This means the new function is SHRUNK vertically compared to f(x).

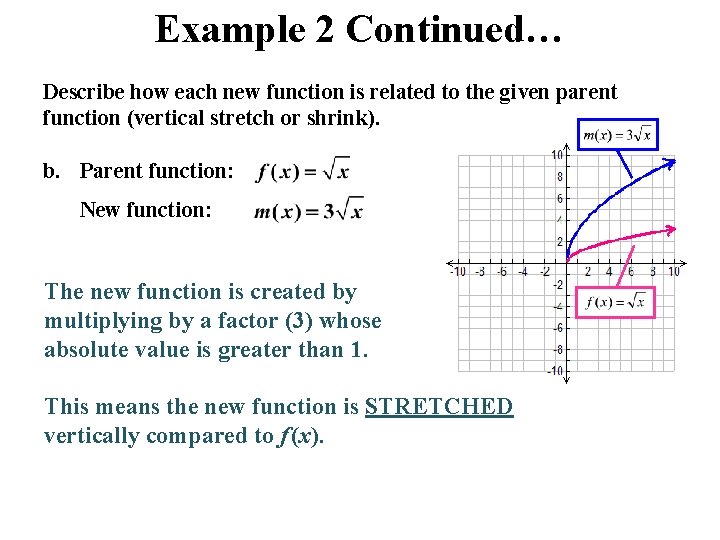
Example 2 Continued… Describe how each new function is related to the given parent function (vertical stretch or shrink). b. Parent function: New function: The new function is created by multiplying by a factor (3) whose absolute value is greater than 1. This means the new function is STRETCHED vertically compared to f (x).

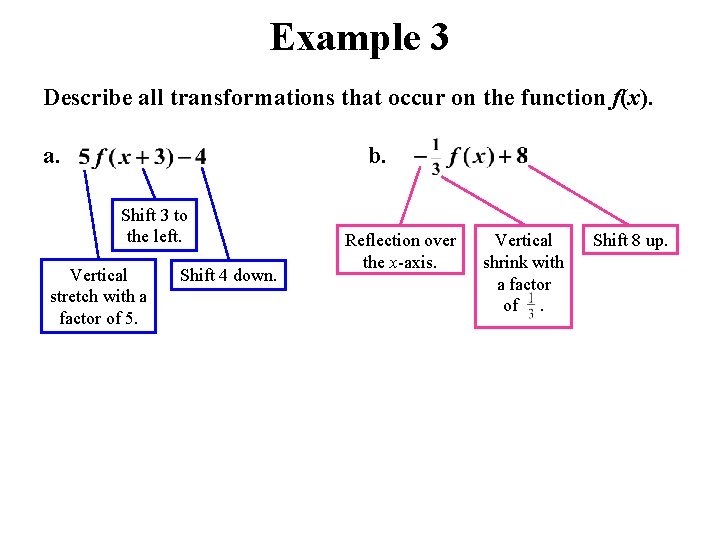
Example 3 Describe all transformations that occur on the function f(x). a. b. Shift 3 to the left. Vertical stretch with a factor of 5. Shift 4 down. Reflection over the x-axis. Vertical shrink with a factor of. Shift 8 up.

Communication Prompt If you were to vertically stretch or shrink a geometric figure, would the new image be similar to the original figure? Explain your reasoning.

Exit Problems Describe all transformations that occur on the function f(x). 1. 2. vertical shrink 3. vertical stretch 4. vertical stretch, shift up 1 unit 5. reflection over y-axis, vertical stretch, shift up 6 units reflection over x-axis, vertical shrink