Lesson 1 4 Linear Functions and Models pg

Lesson 1 -4 Linear Functions and Models pg. 19 A rail on the railroad track expands with heat and contracts with the cold. Since its length depends on the temperature. We say that the length is a function of the temperature. If L stands for the length in meters and T stands for the degrees in Celsius , then for a ten meter rail. L and T are related by this formula: L = 0. 0001 T + 10

Activity T (in o C) 0 o 10 o 20 o 30 o 40 o L (in m) (b) Graph the values found in part a using T as the horizontal axis and L as the vertical axis in a coordinate plane. (c) The graph in b above will look much like a ______________ why? ________

Linear functions have the form f(x) = mx + b h(t) = 3 is a linear function because it can be written h(t) = 0 + 3 this special type of function is called a constant function. The graphs of linear functions are straight lines or points on a line.

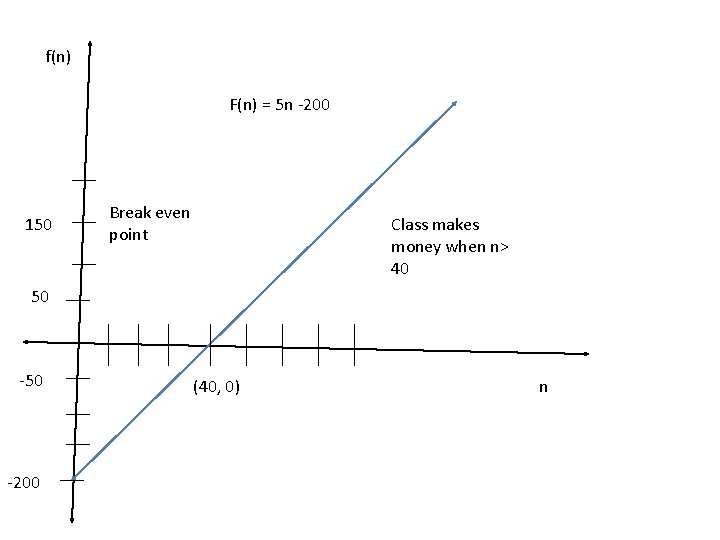
Example 1 The senior class has paid $200 to rent a roller skating rink for a fund raising party. Tickets for the party are $5 each. (a. ) express the net income as a function of tickets sold. B) Graph the function. Identify the point at which the class begins to make a profit.

f(n) F(n) = 5 n -200 150 Break even point Class makes money when n> 40 50 -200 (40, 0) n

The domain is the set of values for which the function is defined. In the function f(n) =5 n -200 in example 1 n represents the number of tickets sold, so the domain is the set of non negative integers. The function f(n) = 5 n -200 is said to model income. A mathematical model is one or more functions, graphs, tables, equations, or inequalities that describe a real world situation.

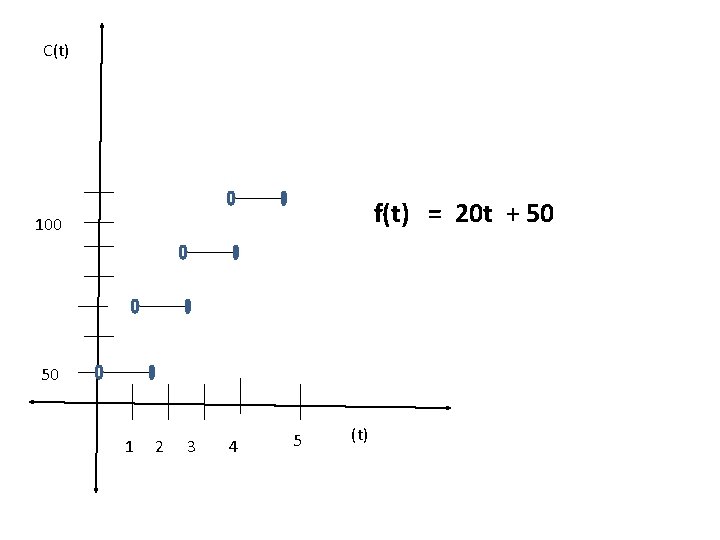
Example 2 Suppose that it costs 50 cents for the first minute of a long-distance telephone call and 20 cents for each additional minute. Or fraction thereof. Give a model for the cost of a call lasting t minutes. Input (Time in minutes) t Output ( cost in cents) C(t) 0 < t and t ≤ 1 50 1< t and t ≤ 2 50 + 20( 1) = 70 2 < t and t ≤ 3 50 + 20( 2) = 90 3 < t and t ≤ 4 50 + 20( 3) = 110

C(t) f(t) = 20 t + 50 100 50 1 2 3 4 5 (t)

Homework (1 -22) all pp. 22 -25