Lesson 1 3 Exponential Functions 7 Part I

Lesson 1. 3 Exponential Functions 7 Part I HW: page 26: 1 -20 For 19, just use the calculator to determine an exponential model, rather than completing a and b.

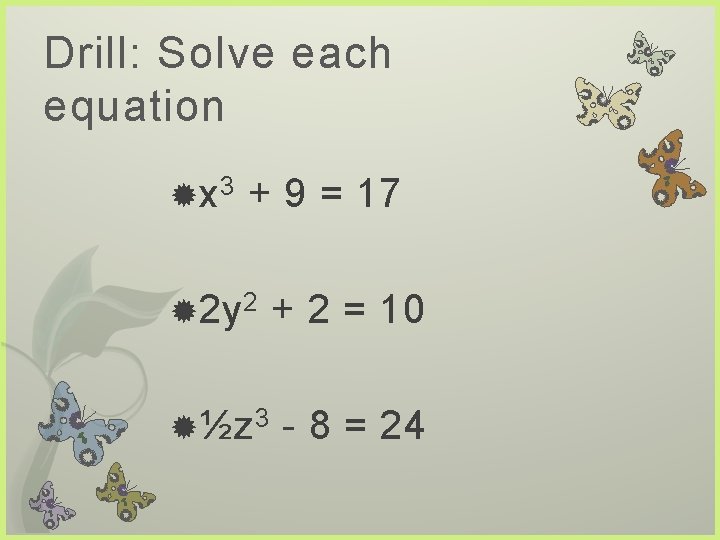
Drill: Solve each equation x 3 + 9 = 17 2 y 2 + 2 = 10 ½z 3 - 8 = 24

Exploration on the graphing calculator: You have 15 minutes to complete this on a separate piece of paper. Graph the function f(x) = a x for a = 2, 3, 5. Use the window [-5, 5] by [-2, 5]. For what values of x is it true that 2 x < 3 x < 5 x ? For what values of x is it true that 2 x > 3 x > 5 x ? For what values of x is it true that 2 x = 3 x = 5 x ? Graph the function y = (1/a) x for a = 2, 3, 5 Repeat parts 2 -4 for the function in part 5.

Exponent Rules Product of Powers Postulate Power of a Power Postulate (a x /a y ) = a x - y Power of a Quotient Postulate (ab) x = a x b x Quotient of Powers Postulate (a x ) y = a x y Power of a Product Postulate ax ● ay = ax+y (a/b) x = a x / b x Zero Exponent Theorem a 0 = 1

Exponential Function Let ‘a’ by a positive real number other than 1. The function f(x) = a x is the exponential function with base a. Graph the function f(x) = 2(3 x ) – 4. State domain and range. X Y -2 -1 0 1 2 -3 -2 -1 Domain: all real numbers (-∞, ∞) 16 14 12 10 8 6 4 2 0 -4 -6 1 2 3

Finding Zeros (xintercepts) Find the zeros of f(x) = 5 x – 2. 5 Let y 1 = f(x) Let y 2 = 0 Graph (standard window is fine…ZOOM 6) 2 nd TRACE, 5, ENTER, ENTER In the case of multiple zeros, you will need to move the cursor towards the other zero(s) before hitting ENTER, ENTER

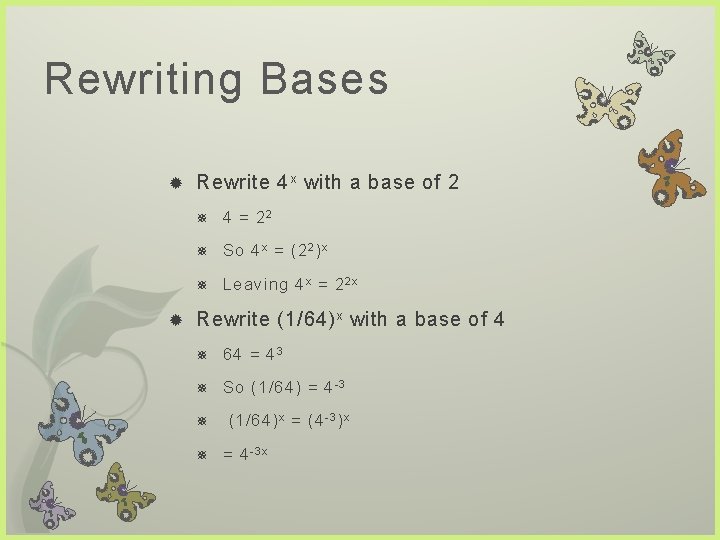
Rewriting Bases Rewrite 4 x with a base of 2 4 = 22 So 4 x = (2 2 ) x Leaving 4 x = 2 2 x Rewrite (1/64) x with a base of 4 64 = 4 3 So (1/64) = 4 -3 (1/64) x = (4 -3 ) x = 4 -3 x

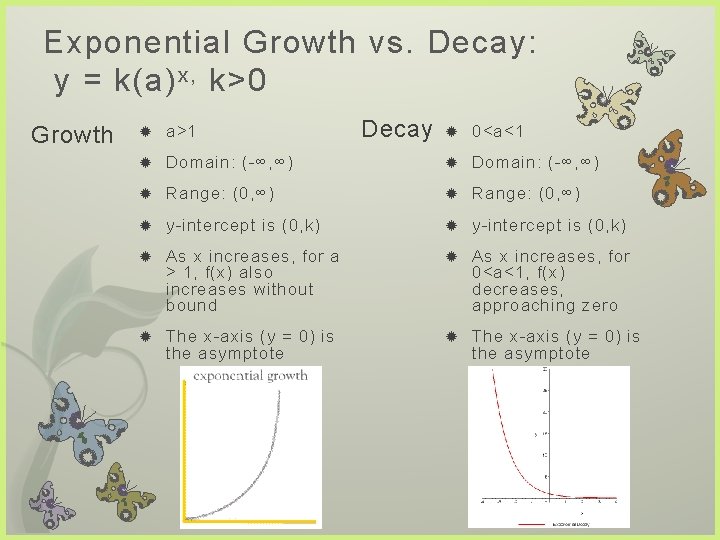
Exponential Growth vs. Decay: y = k(a) x, k>0 Growth a>1 Decay 0<a<1 Domain: (-∞, ∞) Range: (0, ∞) y-intercept is (0, k) As x increases, for a > 1, f(x) also increases without bound As x increases, for 0<a<1, f(x) decreases, approaching zero The x-axis (y = 0) is the asymptote

Predicting Population A. In 1995, the US population was estimated at 264, 000 people and was predicted to grow about 0. 9% a year for the near future. With these assumptions, state a formula for the US population x years after 1995. B. From the formula, estimate the population in 2010.

Cost of a Penn State Education/Semester (Tuition Only) for PA Residents Year Tuition 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2166 2274 2376 2483 2594 2717 2816 2920 3081 3273 3527 4004 4648 x = years after 1991 and y = cost of tuition Pick any two points on your curve. Step 1: Using the formula y = ka x , form a system: Step 2: Divide the equations (higher power/lower power) to find a: Step 3: Substitute a into EITHER equation to find k: 4: Rewrite, substituting a and k:

Using the calculator… 1) Enter data into STAT, 1: edit, L 1 = x, L 2 = y 2) Plot on the calculator: STATPLOT, Type: scatterplot (1 st one), Xlist = L 1, YList = L 2 3) ZOOM, 9: Zoomstat 4) Exponential regression: STAT, →Calc, 0: Exp. Reg 5) To put into Y=: VARS, →Y-Vars, 1: Function, 1: Y 1 6) 9: Zoom. Stat to see line with points

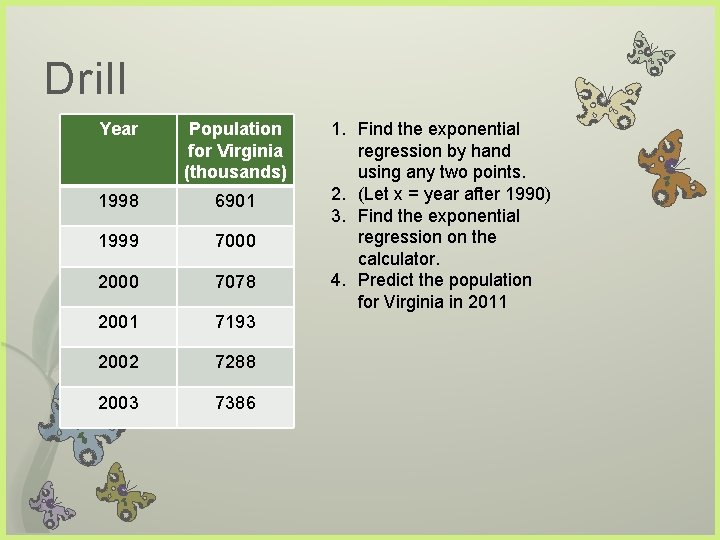
Drill Year Population for Virginia (thousands) 1998 6901 1999 7000 2000 7078 2001 7193 2002 7288 2003 7386 1. Find the exponential regression by hand using any two points. 2. (Let x = year after 1990) 3. Find the exponential regression on the calculator. 4. Predict the population for Virginia in 2011

Half-Life Formula: A = A 0 (. 5) t/h A = final amount after t years. h = half life time period A 0 = original amount A certain substance has a half-life of 24 years. If a sample of 80 grams is being observed, how much will remain in 50 years? A = final amount after 50 years. h = 24 years A 0 = 80 grams A = 80(. 5) 50/24 = 18. 88 grams

compound interest formula: A = P (1 +r/n) n t A = final amount P = original amount R = interest rate N = number of compounding periods T = time A bank is currently offering a certificate of deposit paying 5. 25% interest compounded quarterly. Find the value of the CD after two years if $1000 is invested. A = final amount P = 1000 R = 5. 25 =. 0525 N = 4 T = 2 A = 1000 (1 +. 0525/4) 4 * 2 = $1109. 95

e If the interest were compounded continuously, the amount would approach the irrational number e » 2. 71828…. Continuously Compounded Interest A= P = principal, r = rate, t = years rt Pe

Suppose you invest $100 at 4. 5% interest, compounded continuously, for 5 years. Calculate how much will be in the account. Compare this to an account compounded monthly.

Doubling Time Determine how long it will take for an investment of $P to triple if you compound continuously at a rate of 3. 7% A = Pe rt 3 P = Pe. 037 t 3 = e. 037 t Let y 1 = 3 and y 2 = e. 037 t Intersect (You will need to change windows): t = 29. 69 years

Group activity: copy and complete the tables below. Hand in at the end of class ! x y= 2 x-3 Chang e ∆y 1 -1 --- 2 1 2 3 3 2 4 5 2 x example y = x 2 1 Chang e ∆y --- 2 3 4 x 1 2 3 4 y = -3 x + 4 Change ∆y --- x 1 2 3 4 y = 3 ex Ratio (yi / yi-1) ---