Lesson 1 3 Angles 1 Angle and Points

Angle and Points • An Angle is a figure formed by two rays with

Naming an angle: (1) Using 3 points (2) Using 1 point (3) Using a

Naming an Angle - continued Using a number: A number (without a degree symbol)

Example l K is the vertex of more than one angle. Therefore, there is

4 Types of Angles Acute Angle: an angle whose measure is less than 90.

Measuring Angles l Just as we can measure segments, we can also measure angles.

Adding Angles l. When you want to add angles, use the notation m 1,

Angle Addition Postulate: The sum of the two smaller angles will always equal the

Example: Angle Addition K is interior to MRW, m MRK = (3 x) ,

Angle Bisector An angle bisector is a ray in the interior of an angle

Congruent Angles Definition: If two angles have the same measure, then they are congruent.

Example • Draw your own diagram and answer this question: • If is the

Slides: 14

Download presentation

Lesson 1 -3 Angles 1

Angle and Points • An Angle is a figure formed by two rays with a common endpoint, called the vertex. ray vertex l ray Angles can have points in the interior, in the exterior or on the angle. A E B D C Points A, B and C are on the angle. D is in the interior and E is in the exterior. B is the vertex. 2

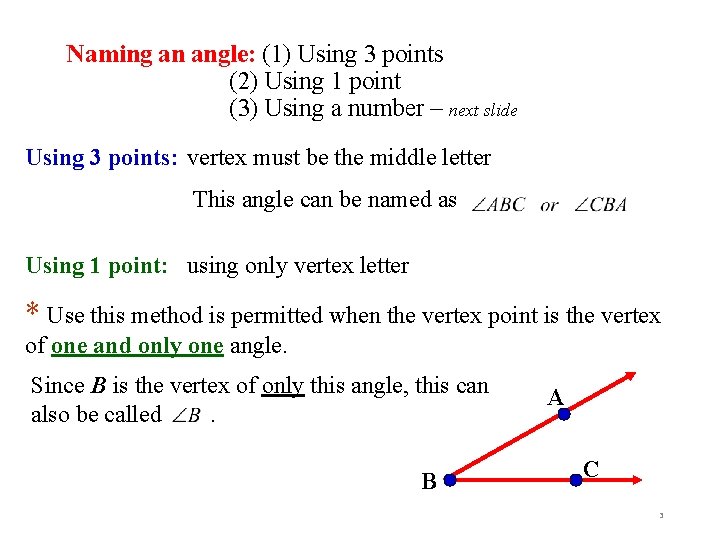
Naming an angle: (1) Using 3 points (2) Using 1 point (3) Using a number – next slide Using 3 points: vertex must be the middle letter This angle can be named as Using 1 point: using only vertex letter * Use this method is permitted when the vertex point is the vertex of one and only one angle. Since B is the vertex of only this angle, this can also be called. B A C 3

Naming an Angle - continued Using a number: A number (without a degree symbol) may be used as the label or name of the angle. This A number is placed in the interior of the angle near its vertex. The angle to the left can be named B 2 C as. * The “ 1 letter” name is unacceptable when … more than one angle has the same vertex point. In this case, use three letter name or a number if it is present. 4

Example l K is the vertex of more than one angle. Therefore, there is NO in this diagram. There is 5

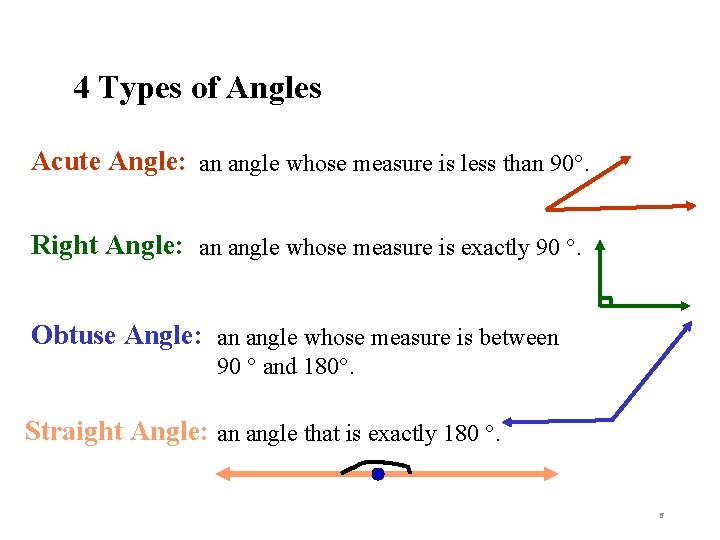
4 Types of Angles Acute Angle: an angle whose measure is less than 90. Right Angle: an angle whose measure is exactly 90 . Obtuse Angle: an angle whose measure is between 90 and 180. Straight Angle: an angle that is exactly 180 . 6

Measuring Angles l Just as we can measure segments, we can also measure angles. l We use units called degrees to measure angles. • 360º ? A circle measures _____ • 180 A (semi) half-circle measures _____ ? º • ? A quarter-circle measures _____ 90º • One degree is the angle measure of 1/360 th of a circle. 7

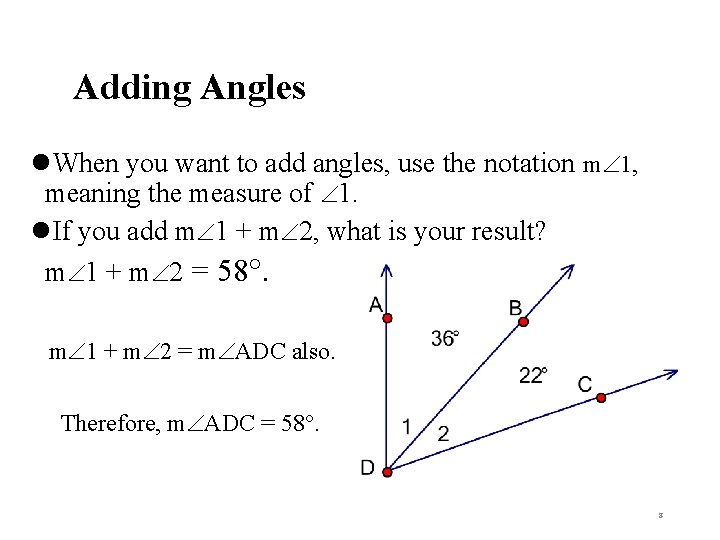
Adding Angles l. When you want to add angles, use the notation m 1, meaning the measure of 1. l. If you add m 1 + m 2, what is your result? m 1 + m 2 = 58. m 1 + m 2 = m ADC also. Therefore, m ADC = 58. 8

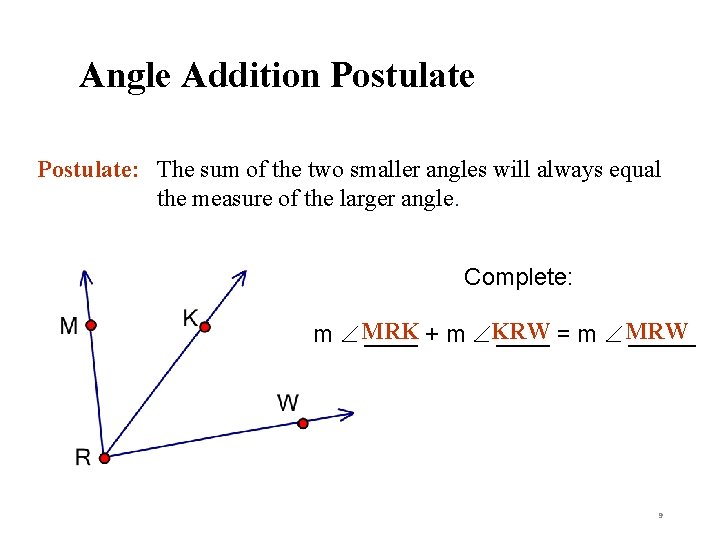
Angle Addition Postulate: The sum of the two smaller angles will always equal the measure of the larger angle. Complete: m MRK ____ + m KRW ____ = m MRW _____ 9

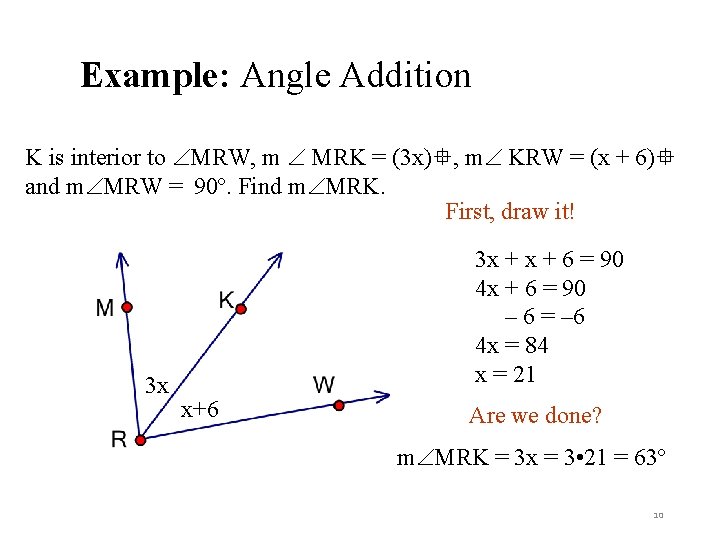
Example: Angle Addition K is interior to MRW, m MRK = (3 x) , m KRW = (x + 6) and m MRW = 90º. Find m MRK. First, draw it! 3 x 3 x + 6 = 90 4 x + 6 = 90 – 6 = – 6 4 x = 84 x = 21 x+6 Are we done? m MRK = 3 x = 3 • 21 = 63º 10

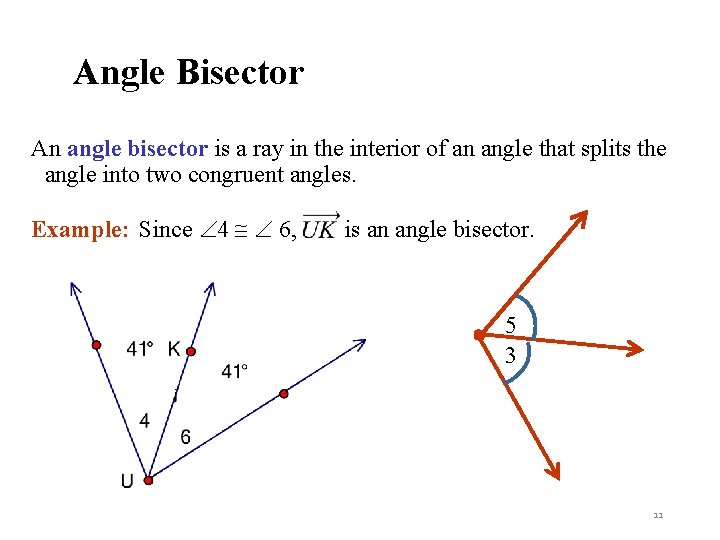
Angle Bisector An angle bisector is a ray in the interior of an angle that splits the angle into two congruent angles. Example: Since 4 6, is an angle bisector. 5 3 11

Congruent Angles Definition: If two angles have the same measure, then they are congruent. Congruent angles are marked with the same number of “arcs”. The symbol for congruence is Example: 3 5 12

Example • Draw your own diagram and answer this question: • If is the angle bisector of PMY and m PML = 87 , then find: • m PMY = _______ • m LMY = _______ 13

Thanks for coming! 14