Lesson 1 1 Properties of Real Numbers Natural

Lesson 1 -1 Properties of Real Numbers

• Natural numbers – the numbers used for counting. • Whole numbers – The natural numbers and zero. • Integers – The natural numbers (also called positive integers) AND their opposites (also called the negative integers), and zero

Rational Numbers – Numbers that can be written as quotients of integers. (fractions) • (Denominator cannot be zero) – Rational numbers can be written as terminating decimals. – Other rational numbers can be written as repeating decimals.

Irrational Numbers • Numbers that cannot be written as quotients of integers. • A decimal that neither terminates or repeats. • If a positive rational number is not a perfect square such as 25 or 4/9, then its square root is irrational.

• Example 1 • Which set of numbers best describes the values for each variable. – The cost C in dollars of admission for n people.


• The opposite or additive inverse of any number a is –a. • The sum of opposites is • The reciprocal or multiplicative inverse of any nonzero number a is 1/a • The product of reciprocals is

• Find the opposite and reciprocal of each number. • 3/5 -3. 2

• What symbols do you use to compare numbers. • Compare ¼ and. 3

• Absolute Value – distance from zero • Note* - Absolute Value is always positive
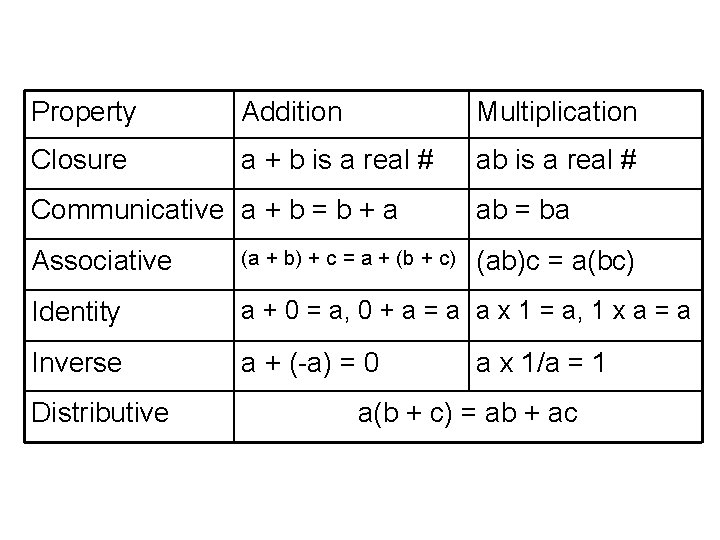
Property Addition Multiplication Closure a + b is a real # ab is a real # Communicative a + b = b + a ab = ba Associative (a + b) + c = a + (b + c) (ab)c = a(bc) Identity a + 0 = a, 0 + a = a a x 1 = a, 1 x a = a Inverse a + (-a) = 0 Distributive a x 1/a = 1 a(b + c) = ab + ac

• Assignment 2 - 54 even , 66, 82, 91 -95 on pgs 8 - 10
- Slides: 12