Lesson 1 1 Patterns Inductive Reasoning Vocabulary Term

Lesson 1 -1: Patterns & Inductive Reasoning

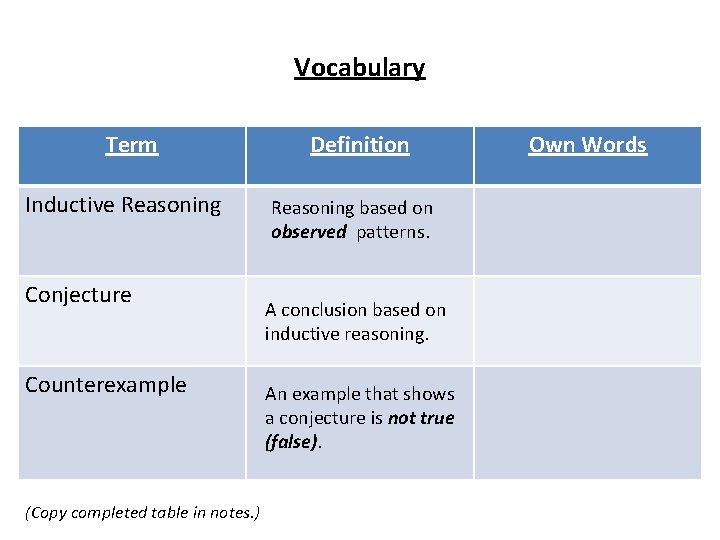
Vocabulary Term Inductive Reasoning Conjecture Counterexample (Copy completed table in notes. ) Definition Reasoning based on observed patterns. A conclusion based on inductive reasoning. An example that shows a conjecture is not true (false). Own Words

2, 3, 5 What will the next number be? • Conjecture: the next number is 8 CONGRATULATIONS!!! You just used inductive reasoning based on what you observed (saw).

• We use inductive reasoning to find patterns • Find patterns from 2 main areas: – Numbers • See what is going on from one number to the next (add, subtract, multiply, divide? ) – Shapes • How does the shape changed: turned? Added parts? removed parts?

In-Class Examples Find the next 2 items in each pattern. 1) 5, 10, 20, 40, … 80 160 2)

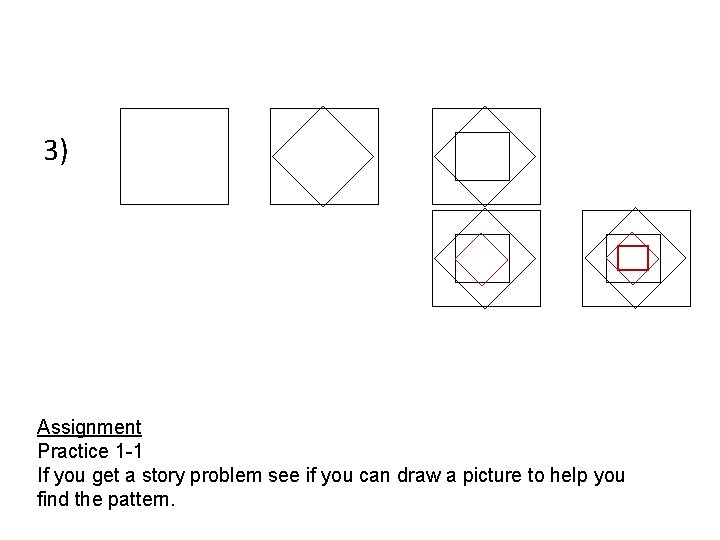
3) Assignment Practice 1 -1 If you get a story problem see if you can draw a picture to help you find the pattern.

• Review our two examples from yesterday about the sunny days and 2, 3, 5. • Were those conjectures correct? • Conjectures are not always true (correct) – They are still conjectures though! • We prove a conjecture is not true by showing a counterexample – Sunny days counterexample: it will rain someday – 2, 3, 5 counterexample: the next number could be 7 or 8 • 7 if your conjecture was prime numbers • 8 if your conjecture was 2 + 3 = 5, so 3 + 5 = 8

• Finding counterexamples: – Find numbers that fit the criteria but do not reach the correct result (conclusion) – Hint: throw the word “not” after the is • Example on page 7: find a counterexample. 25) The sum of two numbers is greater than either number. Need to find two numbers whose sum is not greater than either number. 2 + 3 = 5; 5 > 2 and 5 > 3 … not 2 and 3 No positive numbers work! Let one be negative: -2 + 5 = 3; the sum, 3, is not greater than either number Counterexample: -2 and 5