Lesson 1 1 Patterns and Inductive Reasoning Ohio

Lesson 1 -1 Patterns and Inductive Reasoning

Ohio Content Standards:

Ohio Content Standards: • Estimate, compute and solve problems involving real numbers, including ratio, proportion and percent, and explain solutions. -Demonstrate fluency in computations using real numbers. -Estimate, compute and solve problems involving rational numbers, including ratio, proportion and percent, and judge the reasonableness of solutions.

Ohio Content Standards: • Estimate, compute and solve problems involving real numbers, including ratio, proportion and percent, and explain solutions. -Demonstrate fluency in computations using real numbers. -Estimate, compute and solve problems involving rational numbers, including ratio, proportion and percent, and judge the reasonableness of solutions. • Generalize and explain patterns and sequences in order to find the next term and the nth term.

Vocabulary:

Vocabulary: • Inductive Reasoning –

Vocabulary: • Inductive Reasoning – When you make a conclusion based on a pattern of examples or past events.

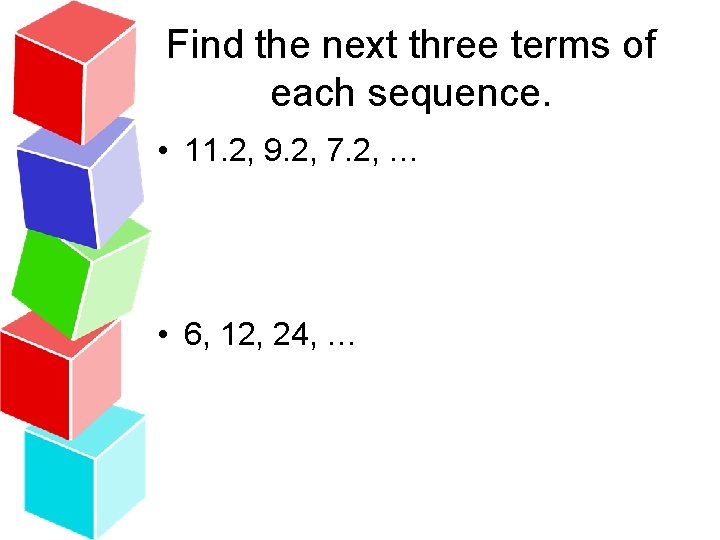
Find the next three terms of each sequence.

Find the next three terms of each sequence. • 11. 2, 9. 2, 7. 2, …

Find the next three terms of each sequence. • 11. 2, 9. 2, 7. 2, … • 6, 12, 24, …

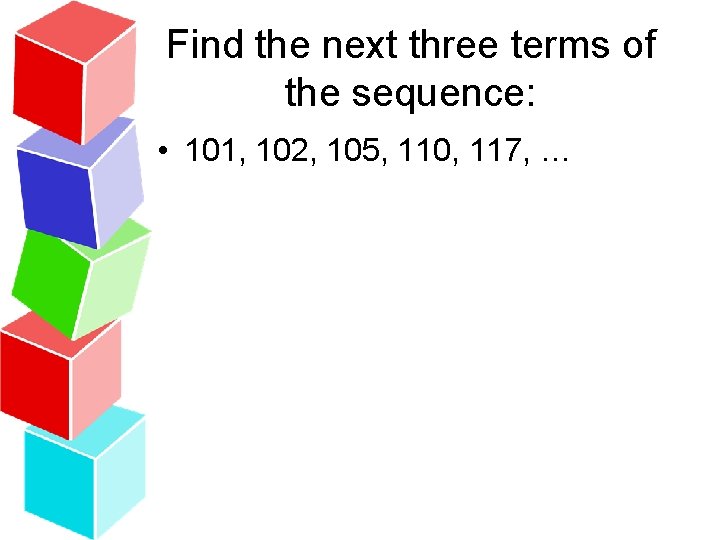
Find the next three terms of the sequence:

Find the next three terms of the sequence: • 101, 102, 105, 110, 117, …

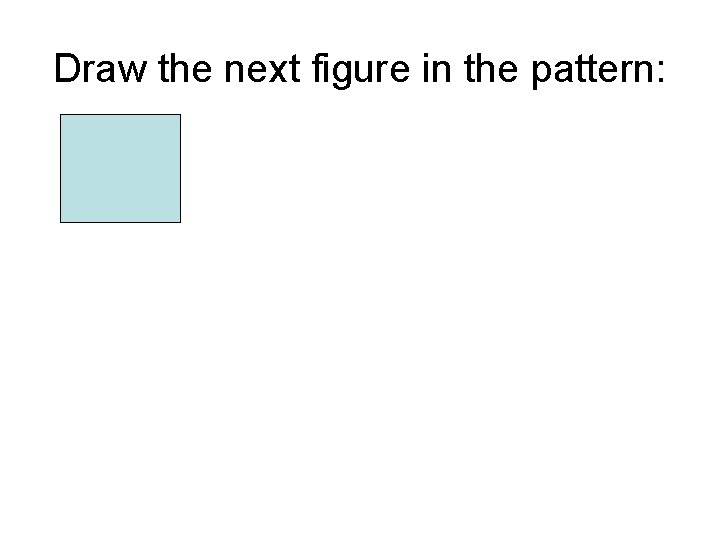
Draw the next figure in the pattern:

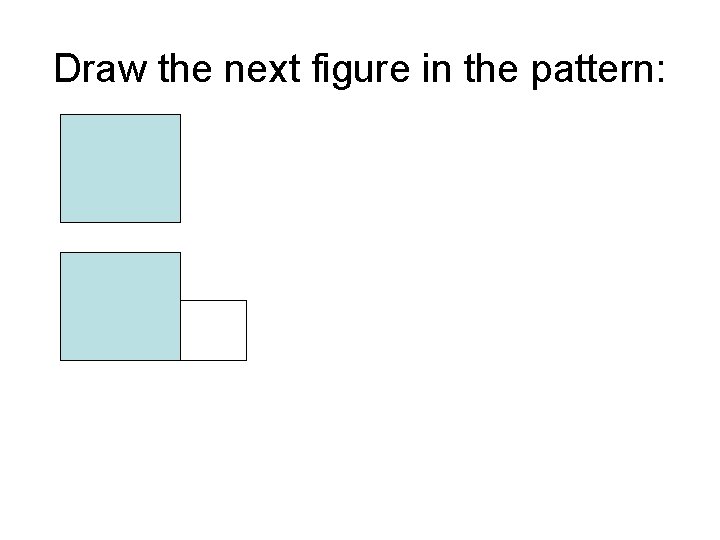
Draw the next figure in the pattern:

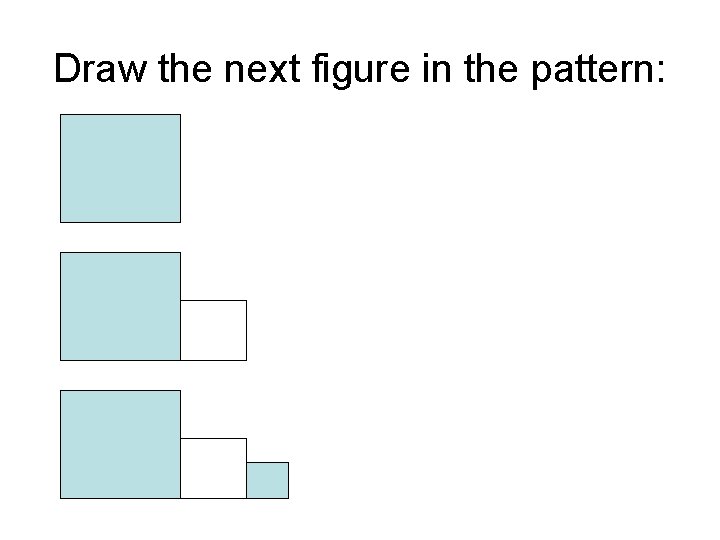
Draw the next figure in the pattern:

Draw the next figure in the pattern:

Vocabulary:

Vocabulary: • Conjecture –

Vocabulary: • Conjecture – A conclusion that you reach based on inductive reasoning.

Vocabulary: • Conjecture – A conclusion that you reach based on inductive reasoning. • Counterexample –

Vocabulary: • Conjecture – A conclusion that you reach based on inductive reasoning. • Counterexample – an example that does not follow the conjecture, proving the conjecture false.

Jordan studied the data below and made the following conjecture:

Jordan studied the data below and made the following conjecture: • Multiplying a number by -1 produces a product that is less than -1.

Jordan studied the data below and made the following conjecture: • Multiplying a number by -1 produces a product that is less than -1. 5(-1) = -5 and -5 < -1

Jordan studied the data below and made the following conjecture: • Multiplying a number by -1 produces a product that is less than -1. 5(-1) = -5 and -5 < -1 15(-1) = -15 and -15 < -1

Jordan studied the data below and made the following conjecture: • Multiplying a number by -1 produces a product that is less than -1. 5(-1) = -5 and -5 < -1 15(-1) = -15 and -15 < -1 100(-1) = -100 and -100 < -1

Jordan studied the data below and made the following conjecture: • Multiplying a number by -1 produces a product that is less than -1. 5(-1) = -5 and -5 < -1 15(-1) = -15 and -15 < -1 100(-1) = -100 and -100 < -1 300(-1) = -300 and -300 < -1

Jordan studied the data below and made the following conjecture: • Multiplying a number by -1 produces a product that is less than -1. 5(-1) = -5 and -5 < -1 15(-1) = -15 and -15 < -1 100(-1) = -100 and -100 < -1 300(-1) = -300 and -300 < -1 Find a counter example for his conjecture.

Assignment: Pgs. 7 – 9 2 – 34 evens