Lesson 1 1 Patterns and Inductive Reasoning Inductive

Inductive Reasoning Making conclusions/predictions based on patterns and examples. l Find the next two

Making a Conjecture Make a conclusion based on inductive reasoning. Use the table to

Counterexample (like a contradiction) An example for which the conjecture is incorrect. Conjecture: the

Fun Patterns Find the next character in the sequence J, F, M, A, .

Point l A point does not have an actual size; it represents a location.

Line l l A set of points that extends infinitely in opposite directions and

Collinear Points Collinear points are points that lie on the same line. (The line

Planes l l l A plane is a flat surface that extends indefinitely in

Different planes in a figure: A D B C E H Plane EFGH F

Coplanar Objects Coplanar objects (points, lines, etc. ) are objects that lie on the

Postulate An accepted statement or fact. You accept a postulate as true without proof;

Postulate 1 -1 Through any two points there is exactly one line. t B

Postulate 1 -2 If two lines intersect, then they intersect in exactly one point.

Postulate 1 -3 If two planes intersect, then they intersect in exactly one line.

Postulate 1 -4 Through any three noncollinear points there is exactly one plane. Plane

3 Possibilities of Intersection of a Line and a Plane (1) Line passes through

Slides: 18

Download presentation

Lesson 1 -1 Patterns and Inductive Reasoning

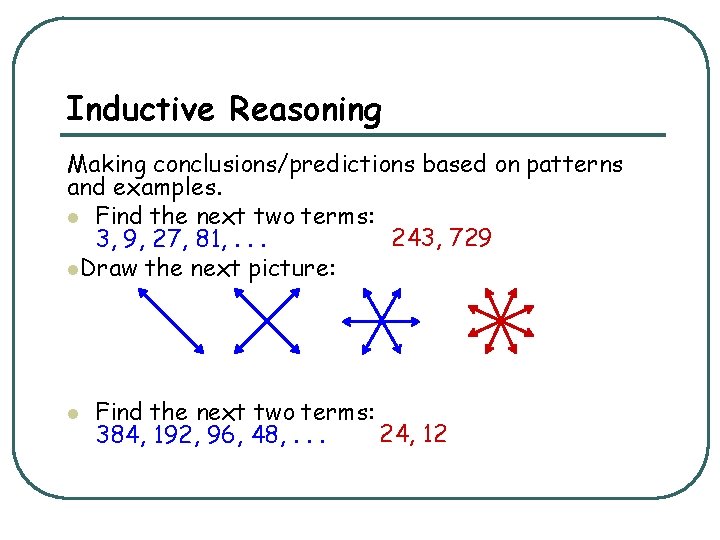
Inductive Reasoning Making conclusions/predictions based on patterns and examples. l Find the next two terms: 243, 729 3, 9, 27, 81, . . . l. Draw the next picture: l Find the next two terms: 24, 12 384, 192, 96, 48, . . .

Making a Conjecture Make a conclusion based on inductive reasoning. Use the table to make a conjecture about the sum of the first six positive even numbers. 2 2+4+6+8 2 + 4 + 6 + 8 + 10 =2 =6 = 12 = 20 = 30 = 1· 2 = 2· 3 = 3· 4 = 4· 5 = 5· 6 = 6· 7 = 42

Counterexample (like a contradiction) An example for which the conjecture is incorrect. Conjecture: the product of two positive numbers is greater than either number. counterexample

Fun Patterns Find the next character in the sequence J, F, M, A, . . . January, February, March, April, May Find the next character in the sequence S, M, T, W, . . . Sunday, Monday, Tuesday, Wednesday, Thursday Find the next character in the sequence Z, O, T, T, F, F, S, S, . . . Zero, One, Two, Three, Four, Five, Six, Seven, Eight Find the next character in the sequence 3, 3, 5, 4, 4, . . . One has 3 letters, Two has 3, Three has 5, Four has 4, Five has 5, Six has 3

Lesson 1 -2 Points, Lines, and Planes

Point l A point does not have an actual size; it represents a location. A How to Sketch: l Use dots How to label: l B Use CAPITAL letters l Never name two points with the same letter (in the same sketch). C A

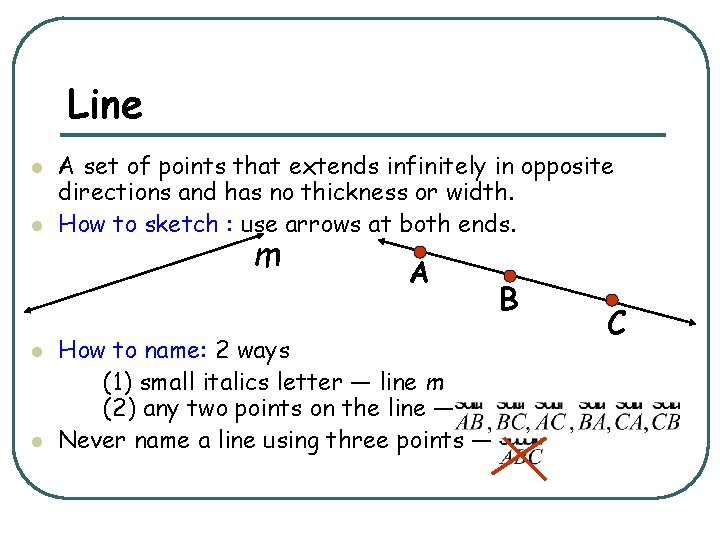
Line l l A set of points that extends infinitely in opposite directions and has no thickness or width. How to sketch : use arrows at both ends. m A How to name: 2 ways (1) small italics letter — line m (2) any two points on the line — Never name a line using three points — B C

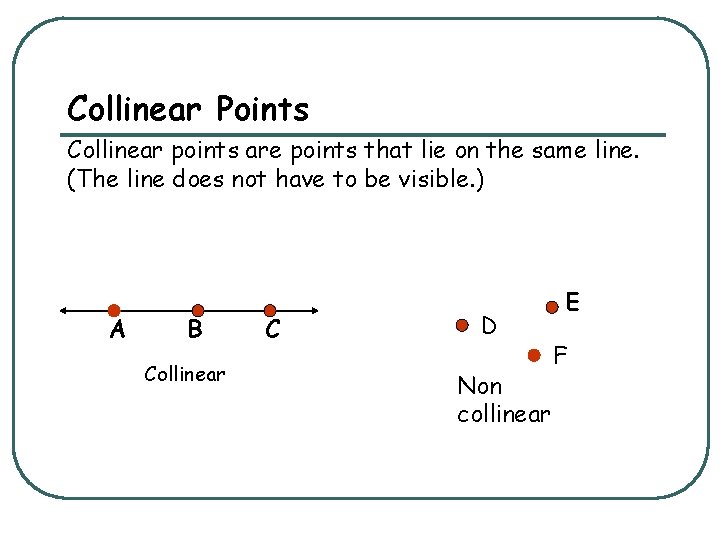
Collinear Points Collinear points are points that lie on the same line. (The line does not have to be visible. ) A B Collinear C D Non collinear E F

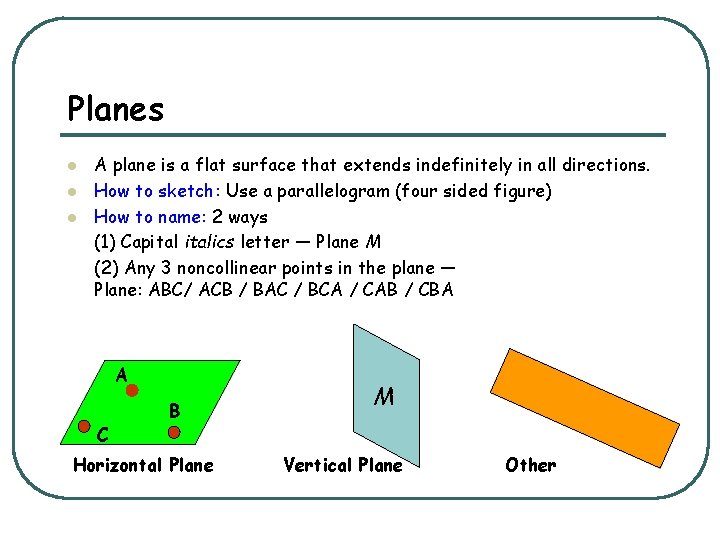
Planes l l l A plane is a flat surface that extends indefinitely in all directions. How to sketch: Use a parallelogram (four sided figure) How to name: 2 ways (1) Capitalics letter — Plane M (2) Any 3 noncollinear points in the plane — Plane: ABC/ ACB / BAC / BCA / CAB / CBA A C B Horizontal Plane M Vertical Plane Other

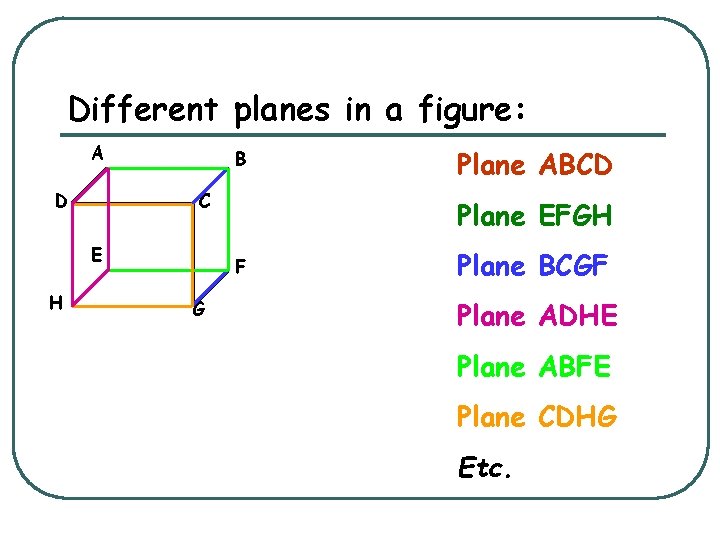
Different planes in a figure: A D B C E H Plane EFGH F G Plane ABCD Plane BCGF Plane ADHE Plane ABFE Plane CDHG Etc.

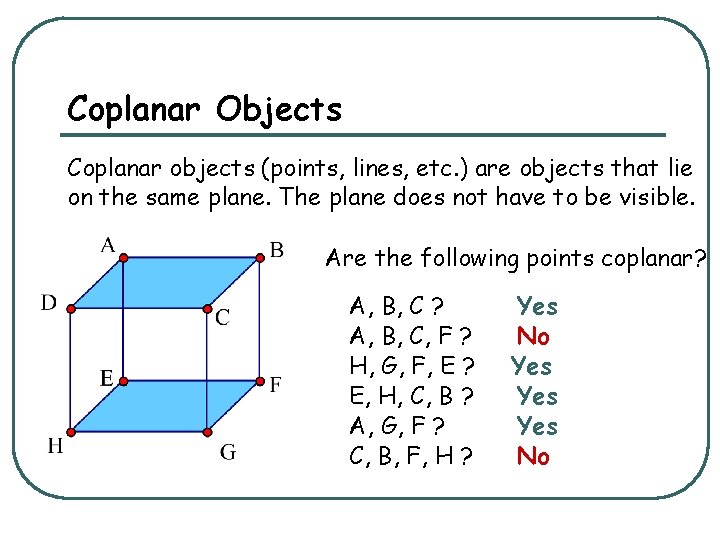
Coplanar Objects Coplanar objects (points, lines, etc. ) are objects that lie on the same plane. The plane does not have to be visible. Are the following points coplanar? A, B, C, F ? H, G, F, E ? E, H, C, B ? A, G, F ? C, B, F, H ? Yes No Yes Yes No

Postulate An accepted statement or fact. You accept a postulate as true without proof; you try to determine if a conjecture is true or false.

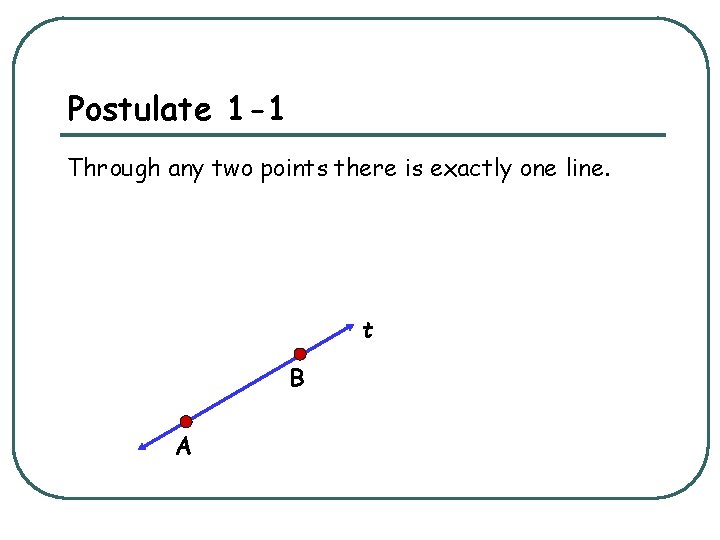
Postulate 1 -1 Through any two points there is exactly one line. t B A

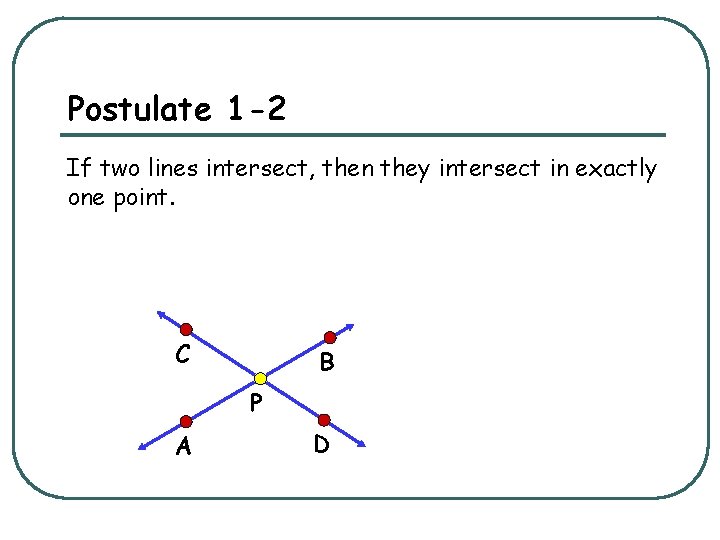
Postulate 1 -2 If two lines intersect, then they intersect in exactly one point. C B P A D

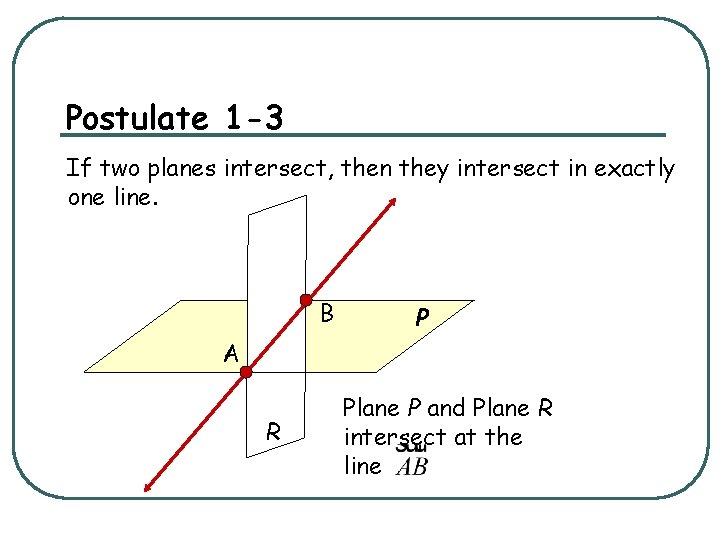
Postulate 1 -3 If two planes intersect, then they intersect in exactly one line. B P A R Plane P and Plane R intersect at the line

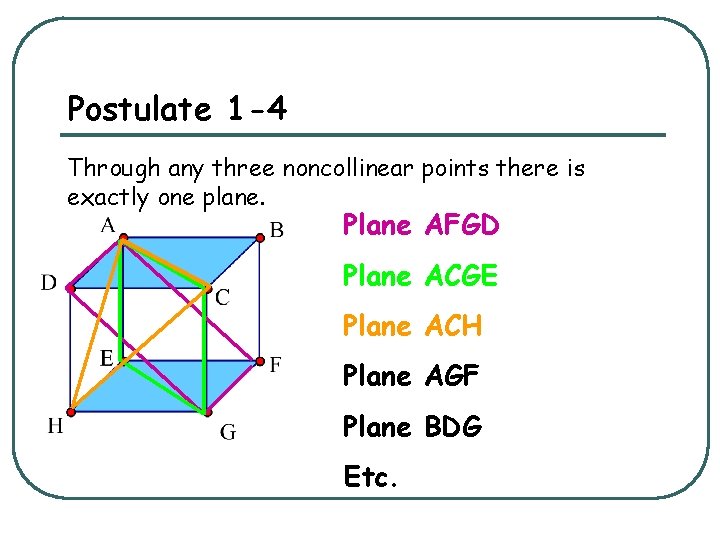
Postulate 1 -4 Through any three noncollinear points there is exactly one plane. Plane AFGD Plane ACGE Plane ACH Plane AGF Plane BDG Etc.

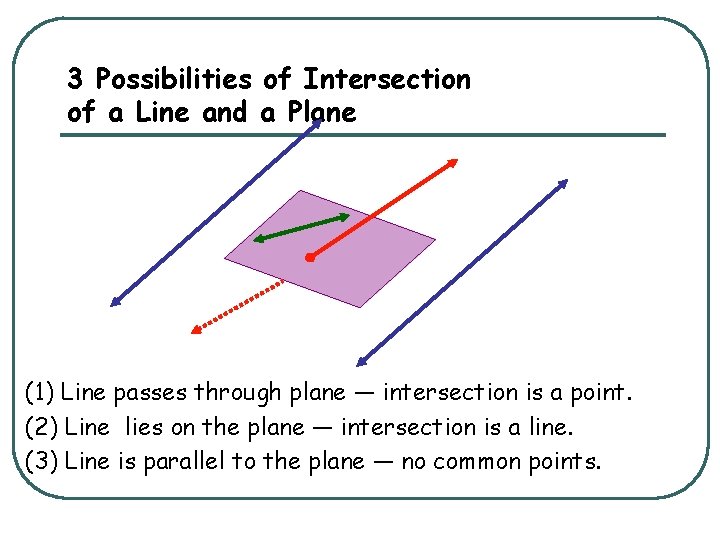
3 Possibilities of Intersection of a Line and a Plane (1) Line passes through plane — intersection is a point. (2) Line lies on the plane — intersection is a line. (3) Line is parallel to the plane — no common points.