Lesson 1 1 Core Focus on Functions Data

Lesson 1. 1 Core Focus on Functions & Data Understanding Functions

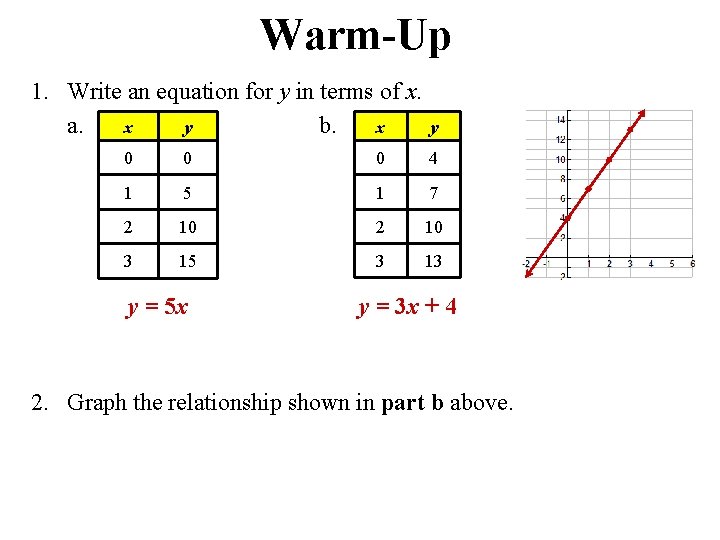
Warm-Up 1. Write an equation for y in terms of x. x y x a. b. y 0 0 0 4 1 5 1 7 2 10 3 15 3 13 y = 5 x y = 3 x + 4 2. Graph the relationship shown in part b above.

Lesson 1. 1 Understanding Functions Determine if a given set of data is a function.

Explore! Dog Years To find the relative age of a dog, some people use the rule of thumb that every year in a dog’s life is equal to seven years in a human’s life. Step 1 Write an equation that shows the relationship between human years (h) and dog years (d). Step 2 Copy the table and fill in the missing values using your equation from Step 1.

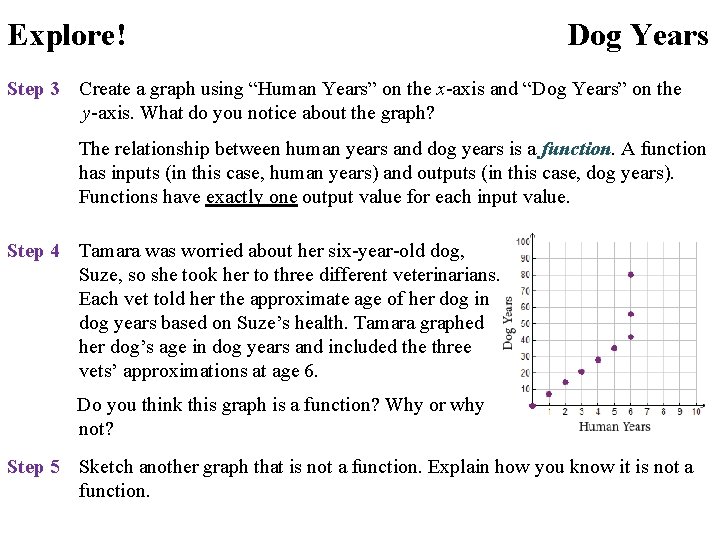
Explore! Dog Years Step 3 Create a graph using “Human Years” on the x-axis and “Dog Years” on the y-axis. What do you notice about the graph? The relationship between human years and dog years is a function. A function has inputs (in this case, human years) and outputs (in this case, dog years). Functions have exactly one output value for each input value. Step 4 Tamara was worried about her six-year-old dog, Suze, so she took her to three different veterinarians. Each vet told her the approximate age of her dog in dog years based on Suze’s health. Tamara graphed her dog’s age in dog years and included the three vets’ approximations at age 6. Do you think this graph is a function? Why or why not? Step 5 Sketch another graph that is not a function. Explain how you know it is not a function.

Vocabulary Function A relationship between two sets of numbers called the input values and output values. Functions have exactly one output value for each input value. Domain The set of input values. Range The set of output values. Vertical Line Test A test used to determine if a graph represents a function by checking to see if a vertical line passes through no more than one point of the graph of a relationship.

Example 1 Give the domain and range of each relationship. Determine if the relationship is a function. a. Input Output The domain is the collection of input values. 2 4 {2, 4, 6, 8} 4 6 6 8 8 10 The range is the collection of output values. {4, 6, 8, 10} 2 4 6 8 10 The values in the table represent a function because each input value matches only one output value.

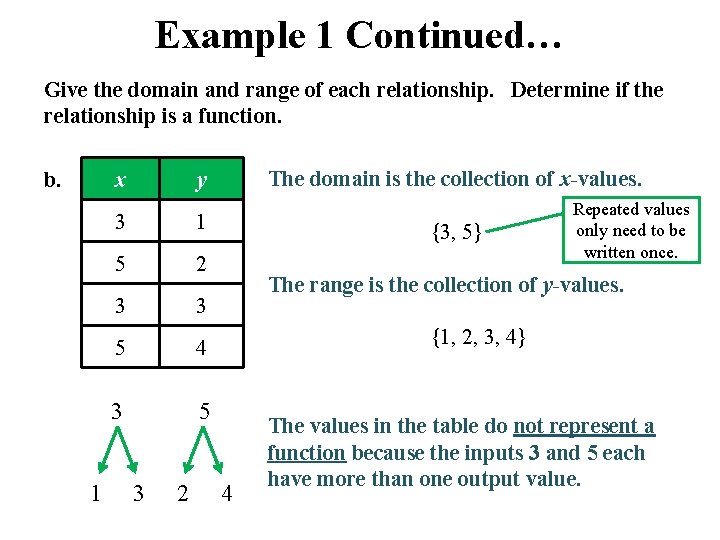
Example 1 Continued… Give the domain and range of each relationship. Determine if the relationship is a function. b. x 1 The domain is the collection of x-values. y 3 1 5 2 3 3 5 4 3 5 3 2 {3, 5} Repeated values only need to be written once. The range is the collection of y-values. {1, 2, 3, 4} 4 The values in the table do not represent a function because the inputs 3 and 5 each have more than one output value.

Example 1 Continued… Give the domain and range of each relationship. Determine if the relationship is a function. c. Input Output 5 7 10 7 15 7 The domain is the collection of input values. {5, 10, 15} The range is the collection of output values. {7} The values in the table represent a function because each input value matches only one output value. 5 10 15 7 7 7

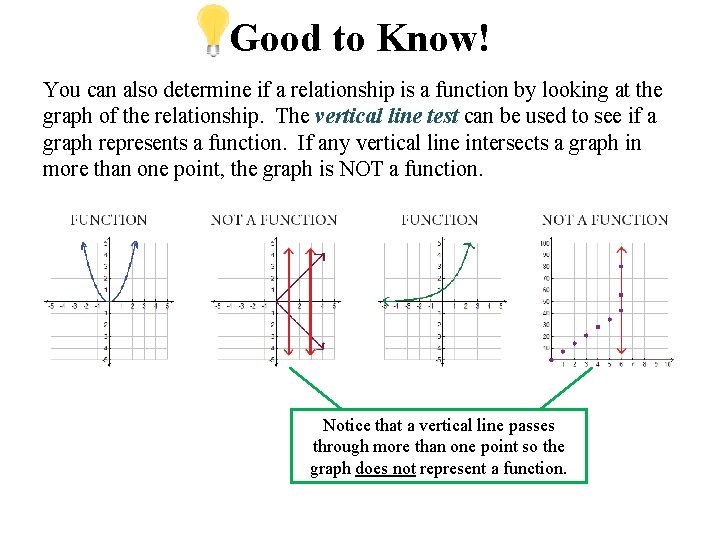
Good to Know! You can also determine if a relationship is a function by looking at the graph of the relationship. The vertical line test can be used to see if a graph represents a function. If any vertical line intersects a graph in more than one point, the graph is NOT a function. Notice that a vertical line passes through more than one point so the graph does not represent a function.

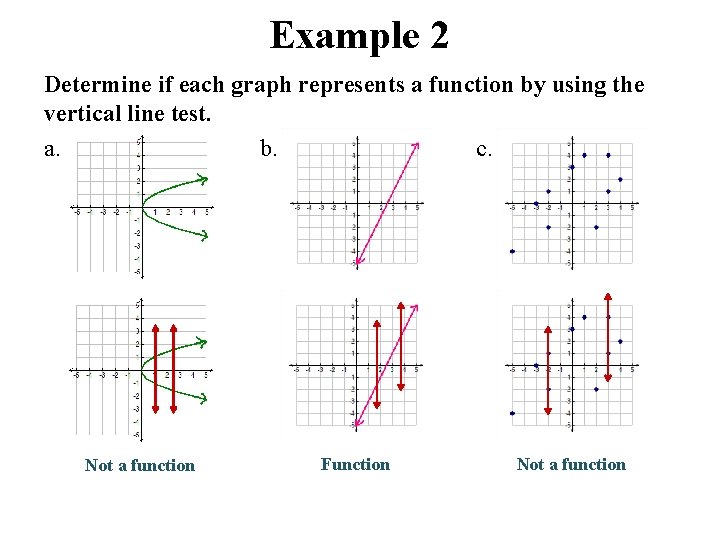
Example 2 Determine if each graph represents a function by using the vertical line test. a. b. c. Not a function Function Not a function

Example 3 James went scuba diving last weekend. He started his dive at sea level. Every minute he went down 20 meters. After 5 minutes, he headed toward the surface at a rate of 20 meters per minute. a. Create a table of values showing his depth under water for each minute of his 10 -minute dive. Time (minutes) 0 Depth (meters) 0 1 2 3 4 5 6 7 8 9 − 20 − 40 − 60 − 80 − 100 − 80 − 60 − 40 − 20 10 0 b. Does this relationship create a function? Why or why not? Yes. This relationship is a function because each minute (input value) is connected to only one output value (or depth).

Communication Prompt Describe in words how you can tell if a relationship is a function based on a table of values.

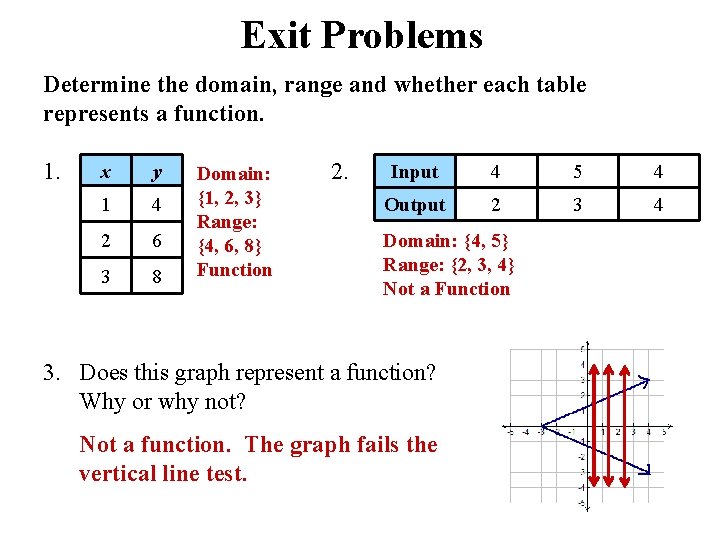
Exit Problems Determine the domain, range and whether each table represents a function. 1. x y 1 4 2 6 3 8 Domain: {1, 2, 3} Range: {4, 6, 8} Function 2. Input 4 5 4 Output 2 3 4 Domain: {4, 5} Range: {2, 3, 4} Not a Function 3. Does this graph represent a function? Why or why not? Not a function. The graph fails the vertical line test.