Less is More Compact Matrix Decomposition for Large

Less is More: Compact Matrix Decomposition for Large Sparse Graphs Jimeng Sun, Yinglian Xie, Hui Zhang, Christos Faloutsos Speaker: Jimeng Sun © 2007 Jimeng Sun

Motivation • Sparse matrices are everywhere # of nonzeros § Network in Amxn = O(m+n) Forensics § Social network analysis § Web graph analysis § Text mining 2 © 2007 Jimeng Sun

Motivation • Sparse matrices are everywhere § Network Forensics § Social network sparse analysismatrices How to summarize in a§ Web concise and intuitive manner? graph analysis § Text mining Compression, Anomaly detection 3 © 2007 Jimeng Sun

Problem: Network forensics • Input: Network flows § <src, dst, # of packets> over time. <128. 2. 175. 2, 128. 2. 175. 184, 128> <128. 2. 1. 2, 128. 2. 175. 184, 128> time <128. 2. 17. 43, 128. 2. 1, 128> … • Output: Useful patterns § Summarize the traffic flows § Identify abnormal traffic patterns 4 © 2007 Jimeng Sun

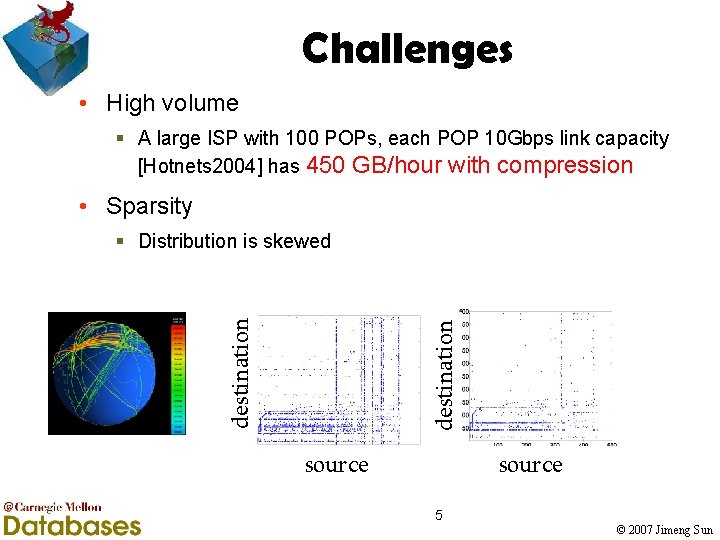
Challenges • High volume § A large ISP with 100 POPs, each POP 10 Gbps link capacity [Hotnets 2004] has 450 GB/hour with compression • Sparsity destination § Distribution is skewed source 5 © 2007 Jimeng Sun

Outline • Motivation • Problem definition • Proposed mining framework § Sparsification § Matrix decomposition § Error Measure • Experiments • Related work • Conclusion 6 © 2007 Jimeng Sun

• Network forensics § Sparsification load shedding § Matrix decomposition summarization § Error Measure anomaly detection 7 © 2007 Jimeng Sun

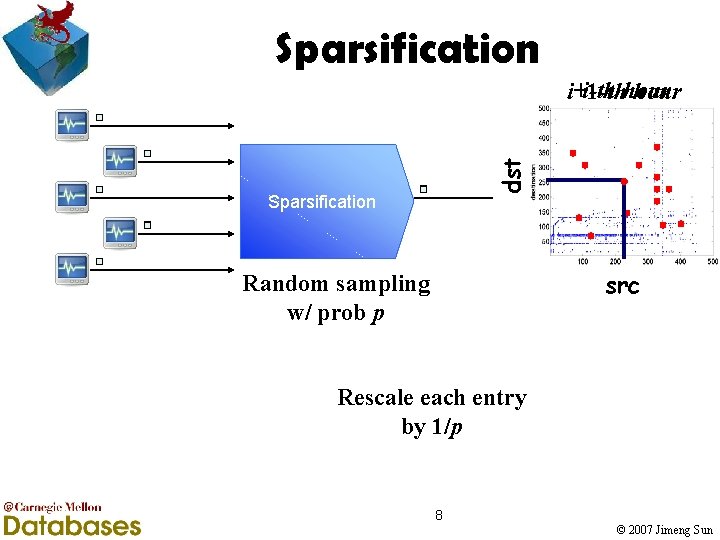
Sparsification dst i-th hour i+1 -th hour Sparsification src Random sampling w/ prob p Rescale each entry by 1/p 8 © 2007 Jimeng Sun

• Network forensics § Sparisfication load shedding § Matrix decomposition summarization § Error Measure anomaly detection 10 © 2007 Jimeng Sun

Matrix decomposition • Goal: Summarize traffic matrices • Why? Anomaly detection • How? § Singular Value Decomposition (SVD) - existing § CUR Decomposition - existing § Compact Matrix Decomposition (CMD) - new 11 © 2007 Jimeng Sun

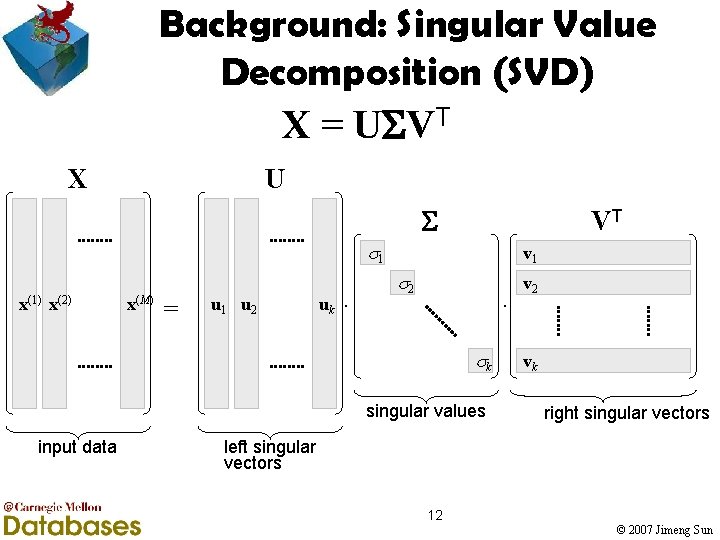
Background: Singular Value Decomposition (SVD) X = U VT X U VT 1 x(1) x(2) x(M) = u 1 u 2 uk . v 1 2 . k singular values input data v 2 vk right singular vectors left singular vectors 12 © 2007 Jimeng Sun

Background: SVD applications • Low-rank approximation • Pseudo-inverse: M+= V -1 UT • Principle component analysis • Latent semantic indexing • Webpage ranking: Kleinberg’s HITS score 13 © 2007 Jimeng Sun

Pros and cons of SVD + Optimal low-rank approximation - 1 st left sing vector • in L 2 and Frobenius norm Interpretability problem: § A singular vector specifies a linear combination of all input columns or rows. Lack of Sparsity § Singular vectors are usually dense VT = U 14 © 2007 Jimeng Sun

Matrix decomposition • Goal: Summarize traffic matrices • Why? Anomaly detection • How? × Singular Value Decomposition (SVD) - existing § CUR Decomposition - existing § Compact Matrix Decomposition (CMD) - new 15 © 2007 Jimeng Sun

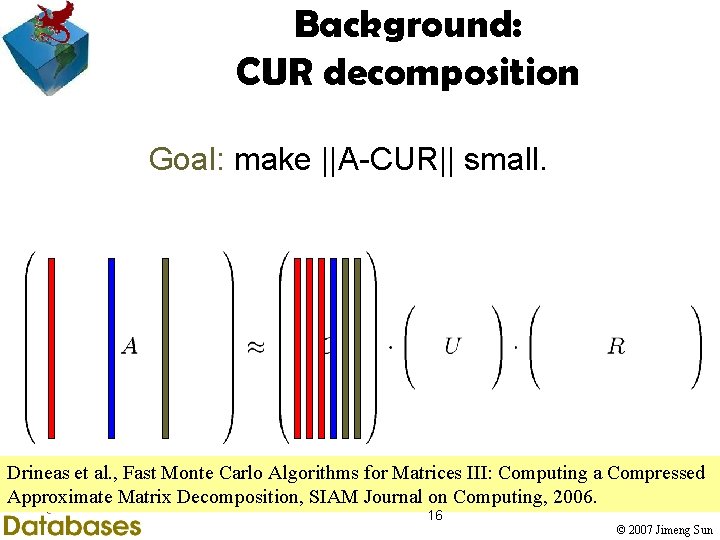
Background: CUR decomposition Goal: make ||A-CUR|| small. Drineas et al. , Fast Monte Carlo Algorithms for Matrices III: Computing a Compressed Approximate Matrix Decomposition, SIAM Journal on Computing, 2006. 16 © 2007 Jimeng Sun

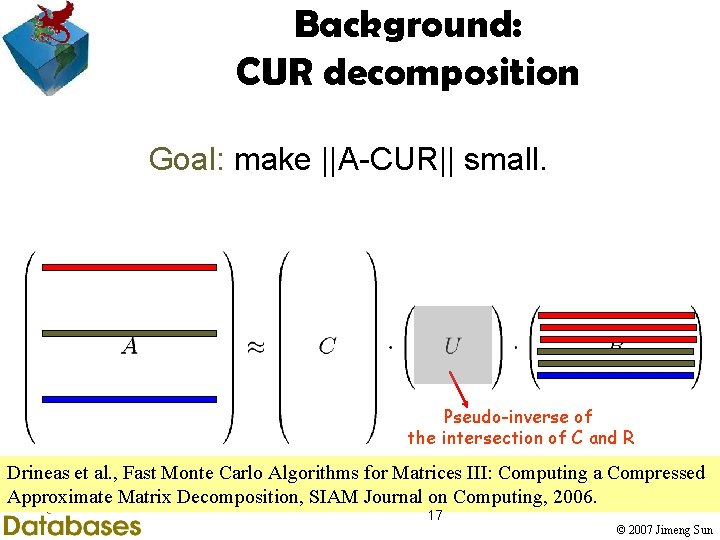
Background: CUR decomposition Goal: make ||A-CUR|| small. Pseudo-inverse of the intersection of C and R Drineas et al. , Fast Monte Carlo Algorithms for Matrices III: Computing a Compressed Approximate Matrix Decomposition, SIAM Journal on Computing, 2006. 17 © 2007 Jimeng Sun

CUR: provably good approximation to SVD • Assume Ak is the “best” rank k approximation to A (through SVD). Thm [Drineas et al. ] CUR in O(mn) time achieves § ||A-CUR|| <= ||A-Ak||+ ||A|| with probability at least 1 - , by picking § O( k log(1/ ) / 2 ) columns, and § O( k 2 log 3(1/ ) / 6 ) rows Drineas et al. , Fast Monte Carlo Algorithms for Matrices III: Computing a Compressed Approximate Matrix Decomposition, SIAM Journal on Computing, 2006. 18 © 2007 Jimeng Sun

Background: CUR applications • DNA SNP Data analysis • Recommendation system • Fast kernel approximation 1. Intra- and interpopulation genotype reconstruction from tagging SNPs, P. Paschou, M. W. Mahoney, A. Javed, J. R. Kidd, A. J. Pakstis, S. Gu, K. K. Kidd, and P. Drineas, Genome Research, 17(1), 96 -107 (2007) 2. Tensor-CUR Decompositions For Tensor-Based Data, M. W. Mahoney, M. Maggioni, and P. Drineas, Proc. 12 -th Annual SIGKDD, 327 -336 (2006) 19 © 2007 Jimeng Sun

Pros and cons of CUR + Easy interpretation • Since the basis vectors are actual columns and rows + Sparse basis • Since the basis vectors are actual columns and rows Actual column Singular vector - Duplicate columns and rows • Columns of large norms will be sampled many times 20 © 2007 Jimeng Sun

Matrix decomposition • Goal: Summarize traffic matrices • Why? Anomaly detection • How? × Singular Value Decomposition (SVD) – existing × CUR Decomposition - existing § Compact Matrix Decomposition (CMD) - new 21 © 2007 Jimeng Sun

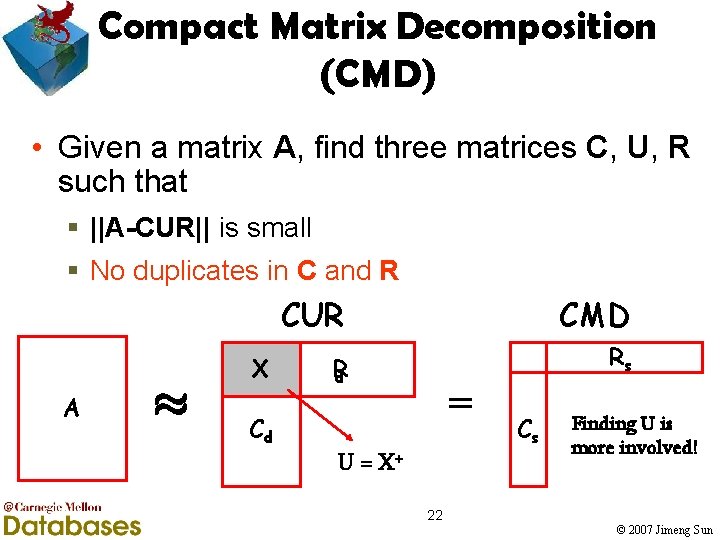
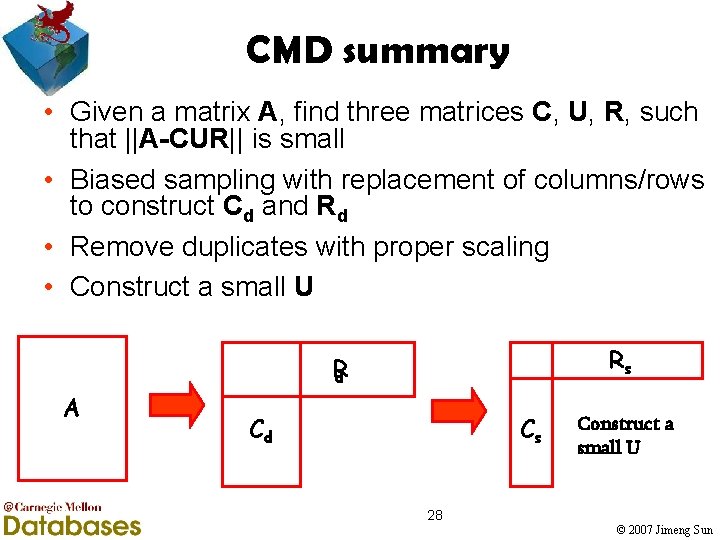
Compact Matrix Decomposition (CMD) • Given a matrix A, find three matrices C, U, R such that § ||A-CUR|| is small § No duplicates in C and R A ¼ X Cd CUR CMD R d Rs = U = X+ Cs Finding U is more involved! 22 © 2007 Jimeng Sun

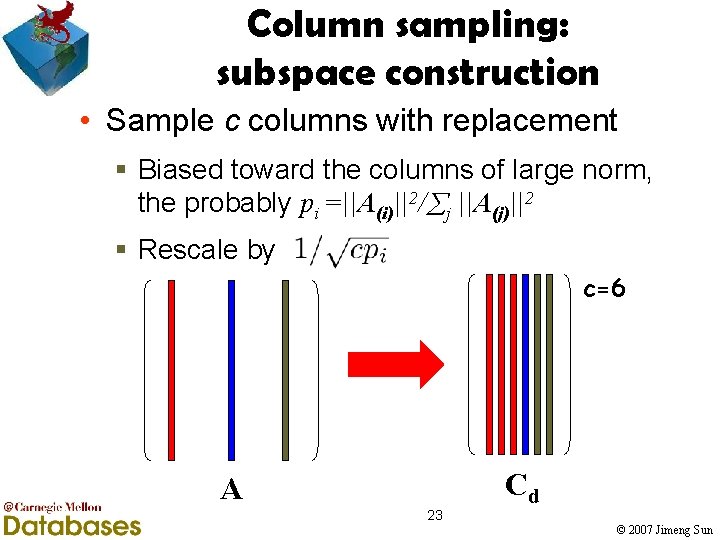
Column sampling: subspace construction • Sample c columns with replacement § Biased toward the columns of large norm, the probably pi =||A(i)||2/ j ||A(j)||2 § Rescale by c=6 A 23 Cd © 2007 Jimeng Sun

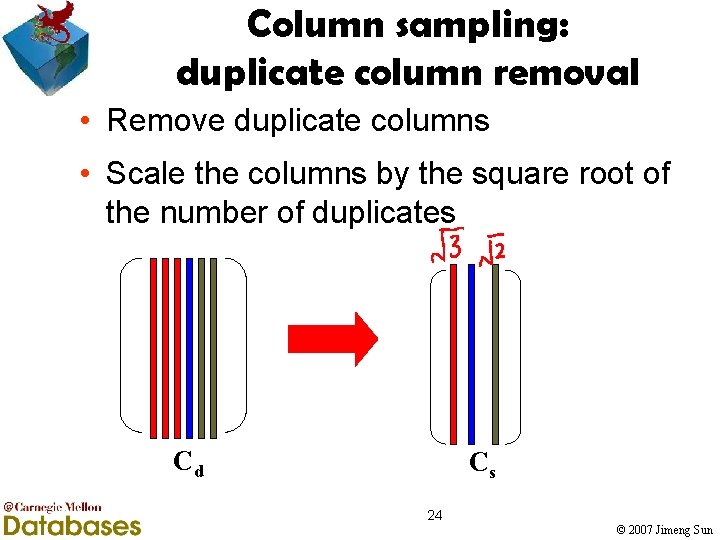
Column sampling: duplicate column removal • Remove duplicate columns • Scale the columns by the square root of the number of duplicates Cd Cs 24 © 2007 Jimeng Sun

Column sampling: correctness proof Thm: Matrix Cs and Cd have the same singular values and left singular vectors § See our paper for the proof Implication: Column duplicate removal preserves the sample top-k subspace 25 © 2007 Jimeng Sun

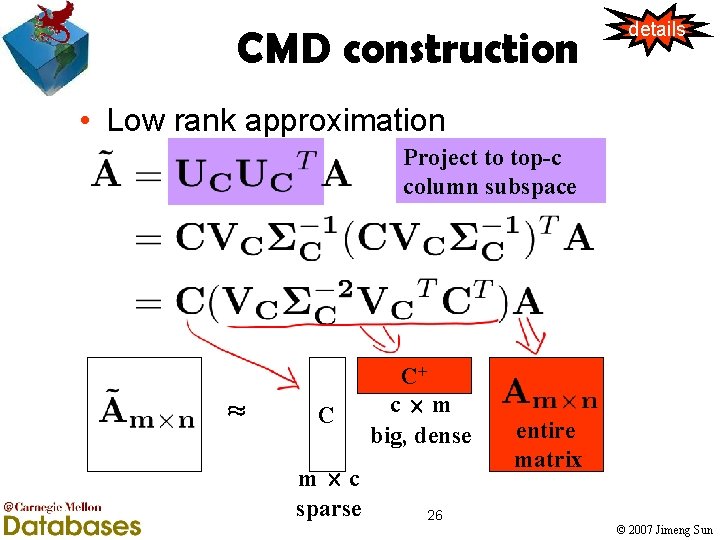
CMD construction details • Low rank approximation Project to top-c column subspace ¼ C m£c sparse C+ c£m big, dense entire matrix 26 © 2007 Jimeng Sun

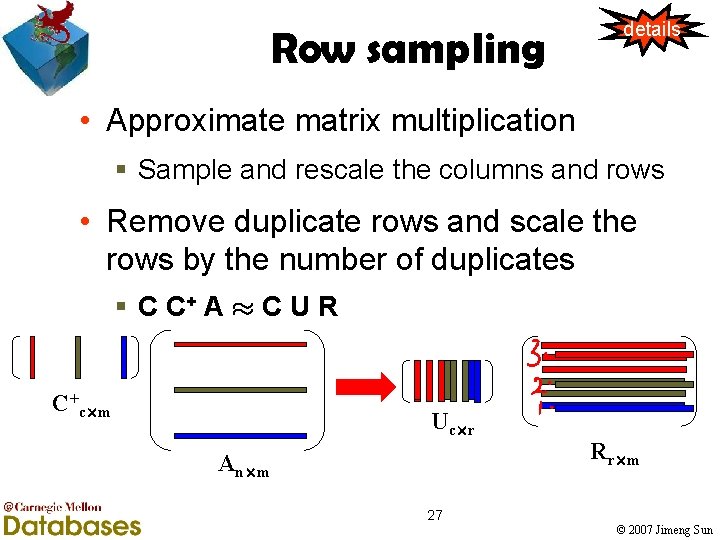
Row sampling details • Approximate matrix multiplication § Sample and rescale the columns and rows • Remove duplicate rows and scale the rows by the number of duplicates § C C+ A ¼ C U R C+c£m Uc£r An£m Rr£m 27 © 2007 Jimeng Sun

CMD summary • Given a matrix A, find three matrices C, U, R, such that ||A-CUR|| is small • Biased sampling with replacement of columns/rows to construct Cd and Rd • Remove duplicates with proper scaling • Construct a small U Rs R d A Cd Cs Construct a small U 28 © 2007 Jimeng Sun

• Network forensics § Sparsification load shedding § Matrix decomposition summarization § Error Measure anomaly detection 29 © 2007 Jimeng Sun

Error Measure • True error • Approximated error for some sample elements in a set S 30 © 2007 Jimeng Sun

Outline • Motivation • Problem definition • Proposed mining framework § Sparsification § Matrix decomposition § Error Measure • Experiments • Related work • Conclusion 31 © 2007 Jimeng Sun

Experiment datasets • Network flow data § 22 k x 22 k matrices § Every matrix corresponds to 1 hour of data § Elements are the log(packet count +1) § 1200 hours, 500 GB raw trace • DBLP bibliographic data § Author-conference graphs from 1980 to 2004 § 428 K authors, 3659 conferences § Elements are the numbers of papers published by the authors 32 © 2007 Jimeng Sun

Experiment design 1. CMD vs. SVD, CUR w. r. t. § Space § CPU time § Accuracy = 1 – relative sum square error 2. Evaluation of other modules § Sparsification, Error measure 3. Case-study on network anomaly detection 33 © 2007 Jimeng Sun

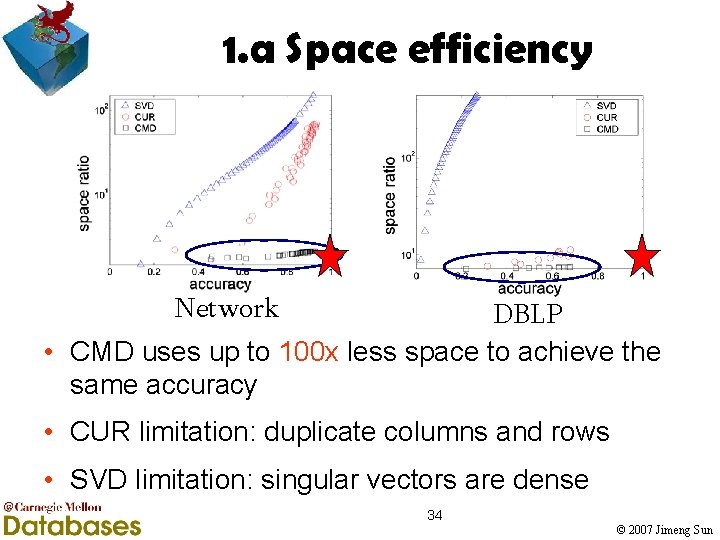
1. a Space efficiency Network DBLP • CMD uses up to 100 x less space to achieve the same accuracy • CUR limitation: duplicate columns and rows • SVD limitation: singular vectors are dense 34 © 2007 Jimeng Sun

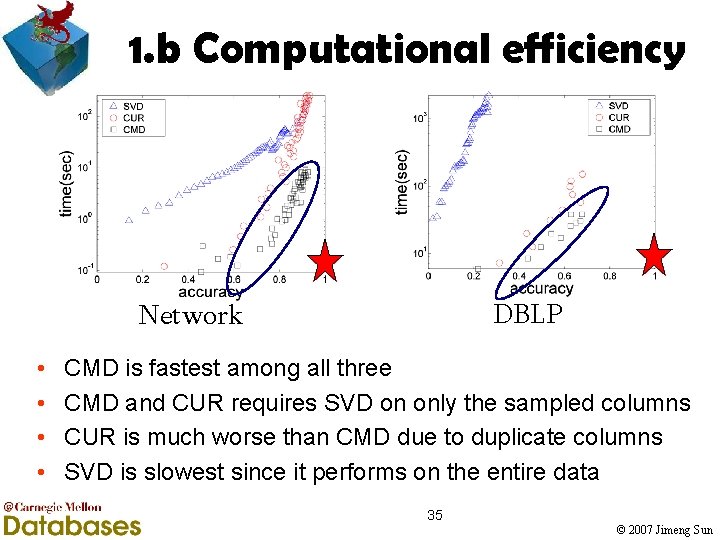
1. b Computational efficiency DBLP Network • • CMD is fastest among all three CMD and CUR requires SVD on only the sampled columns CUR is much worse than CMD due to duplicate columns SVD is slowest since it performs on the entire data 35 © 2007 Jimeng Sun

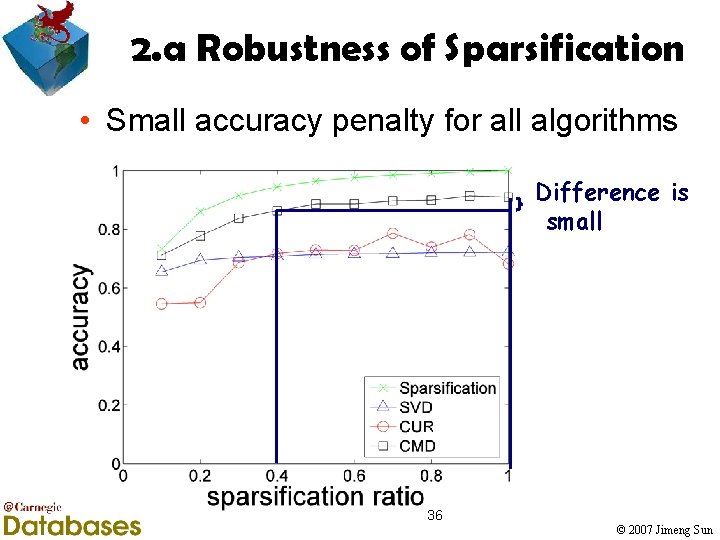
2. a Robustness of Sparsification • Small accuracy penalty for all algorithms Difference is small 36 © 2007 Jimeng Sun

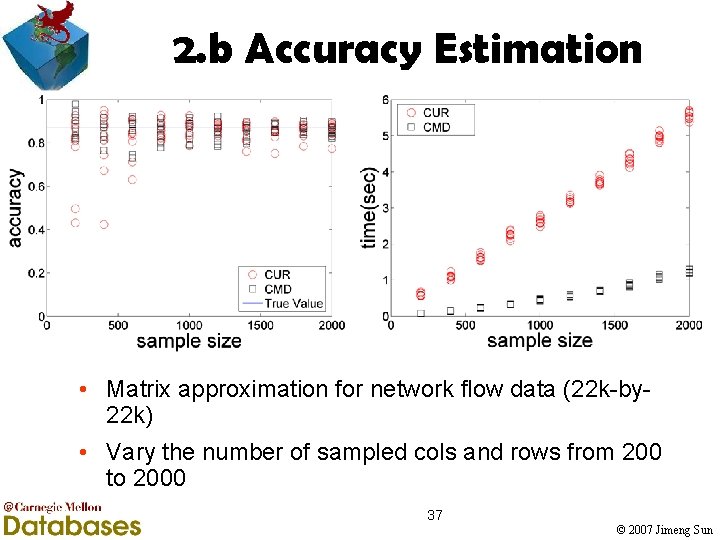
2. b Accuracy Estimation • Matrix approximation for network flow data (22 k-by 22 k) • Vary the number of sampled cols and rows from 200 to 2000 37 © 2007 Jimeng Sun

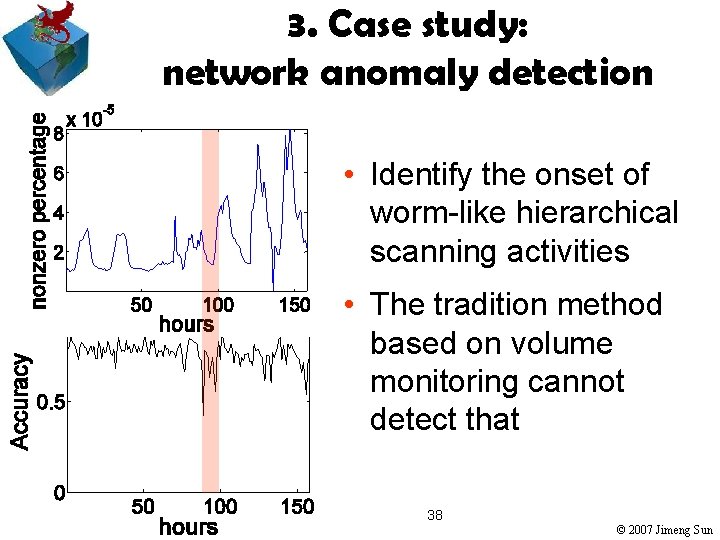
3. Case study: network anomaly detection • Identify the onset of worm-like hierarchical scanning activities • The tradition method based on volume monitoring cannot detect that 38 © 2007 Jimeng Sun

Outline • Motivation • Problem definition • Proposed mining framework § Sparsification § Matrix decomposition § Error Measure • Experiments • Related work • Conclusion 39 © 2007 Jimeng Sun

CUR decompositions Stewart, Berry, Pulatova C: variant of the QR algorithm, No a priori bounds (Num. Math. ’ 99, TOMS’ 05 ) U: minimizes ||A-CUR||F Solid experimental performance Deterministic approach R: variant of the QR algorithm, Goreinov, Tyrtyshnikov, & C: columns that span max volume U: W+ Zamarashkin (LAA ’ 97, Cont. Math. ’ 01) Williams & Seeger R: rows that span max volume Existential result Error bounds depend on ||W+||2 Spectral norm bounds! C: uniformly at random U: W+ R: uniformly at random C: w. r. t. column lengths U: in linear/constant time R: w. r. t. row lengths Experimental evaluation A is assumed PSD Connections to Nystrom method Randomized algorithm Provable, a priori, bounds Explicit dependency on A –Ak Monte-Carlo Sampling approach (NIPS ’ 00) Drineas, Kannan, & Mahoney (SODA ’ 03, ’ 04) Drineas, Mahoney, & Muthukrishnan (’ 05, ’ 06) CMD can help here! (1+ ) approximation to A –A C: depends on singular vectors of A. U: (almost) W+ R: depends on singular vectors of C k Computable in SVDk(A) time. Acknowledge to Petros Drineas for this slide 40 © 2007 Jimeng Sun

Other related work • Low-rank approximation § Frieze, Kannan, Vempala (1998) § Achlioptas and Mc. Sherry (2001) § Sarlós (2006) § Zhang, Zha, Simon (2002) • Other sparse approximations § Sebro, Jaakkola (2004): max-margin matrix factorization § Nonnegative matrix factorization § L 1 regularization 41 © 2007 Jimeng Sun

Conclusion How to summarize sparse matrices in a concise and intuitive manner? Proposed method - CMD 1. Provable accuracy guarantee 2. 10 x to 100 x improvement 3. Interpretability 4. Applied to 500 Gb network forensics data 42 © 2007 Jimeng Sun

Thank you • Contact: § Jimeng Sun § jimeng@cs. cmu. edu • Acknowledgement to Petros Drineas and Michael Mahoney for the insightful discussion/help on CUR decomposition 43 © 2007 Jimeng Sun

The sparsity property sparse and small SVD: A = U Big but sparse T V Big and dense but small CMD: A = C U R Big but sparse 44 © 2007 Jimeng Sun

Column sampling: subspace construction • Biased sampling with replacement of the “large” columns 45 © 2007 Jimeng Sun

Column sampling: duplicate column removal • Remove duplicate columns and scale the column by the square root of the number of duplicates 46 © 2007 Jimeng Sun

Summary on CMD • CMD: A C U R § C/R: sampled and scaled columns and rows without duplicates (sparse) § U: a small matrix (dense) • Properties § Interpretability: interpret matrix by sampled rows and columns § Efficiency: in computation and space • Application § Network forensics: Anomaly detection 47 © 2007 Jimeng Sun

Conclusion How to summarize sparse matrices in a concise and intuitive manner? Theory CMD: low rank approximation 1. sampled and scaled columns and rows without duplicates (sparse) 2. a small matrix (dense) Application Network Forensics 1. Sparsification through sampling 2. Low-rank approximation 3. Error measure CMD: 1. 2. 3. 4. Provable accuracy guarantee 10 x to 100 x improvement Interpretability Applied to 500 Gb network forensics data 48 © 2007 Jimeng Sun