LES VARIABLES ALEATOIRES GENERALITES une variable alatoire est

LES VARIABLES ALEATOIRES

GENERALITES une variable aléatoire est généralement l'ensemble des résultats possibles d'une expérience aléatoire (Exemple: un lancer de dé, un lancer d’un pièce de monnaie, la source générant un signal binaire , , etc). Une variable aléatoire est une description numérique du résultat d'une expérience statistique. Les variables aléatoires sont généralement de nature discrètes ou continues. Des fois elles peuvent être un mélange des deux. Variable aléatoire X discrète Une variable aléatoire qui ne peut prendre qu'un nombre fini ou dénombrable est dite discrète; Exemples: • Une variable aléatoire représentant le nombre de voitures vendues chez un concessionnaire particulier au cours d'une journée serait discrète, • Les valeurs obtenues après des lancers de dé : X = « face du dé » : prend les valeurs x = 1, 2, 3, 4, 5, 6 (dénombrables) • …. etc

GENERALITES Variable aléatoire X continue Une variable aléatoire qui peut prendre n'importe quelle valeur dans un certain intervalle de nombres réels est dit continu. Exemples: • Une variable aléatoire représentant le poids d'une personne en kilogrammes : 50 kg<=X<=100 kg • La température exacte d’un four, • La longueur exacte d’une pièce fabriquée • La date et l'heure de réception d'un paiement.

GENERALITES Variable aléatoire X mélange (continue et discrète simultanément) Une variable aléatoire qui peut prendre en même temps des valeurs discrètes et continues. Exemple: Un récepteur d’une chaine de transmission numérique, reçoit les données numériques binaires émis par l’émetteur mais ‘’corrompues’’ par un bruit blanc dû au canal qui est modélisé souvent comme étant une variable aléatoire continue (Gaussien centré)

STATISTIQUES DES VARIABLES ALEATOIRES Loi de probabilité d’une variable aléatoire X discrète Pour une variable aléatoire discrète, X, la distribution de probabilité est définie par une fonction de masse de probabilité, notée f(xi); où xi l’ensemble des valeurs que la variable aléatoire discrète X peut prendre, Cette fonction fournit la probabilité pour chaque valeur xi de la variable aléatoire X. Dans le développement de la fonction de probabilité pour une variable aléatoire discrète, deux conditions doivent être satisfaites: (1) f(xi ) doit être non négatif pour chaque valeur de la variable aléatoire, 1 f(xi ) 0 (2) la somme des probabilités pour chaque valeur de la variable aléatoire doit être égale à un.

STATISTIQUES DES VARIABLES ALEATOIRES Loi de probabilité d’une variable aléatoire X discrète f(xi ) xi X Densité de probabilité d’une variable aléatoire discrète

STATISTIQUES DES VARIABLES ALEATOIRES Loi de probabilité d’une variable aléatoire X continue Une variable aléatoire continue peut prendre n'importe quelle valeur dans un intervalle de valeurs réelle ou dans une collection d'intervalles. Puisqu'il y a un nombre infini de valeurs dans n'importe quel intervalle, il n'est pas significatif de parler de la probabilité que la variable aléatoire prenne une valeur spécifique; au lieu de cela, la probabilité qu'une variable aléatoire continue se trouve dans un intervalle donné est considérée. P(a X b) = = P(X b) - P(X a) avec
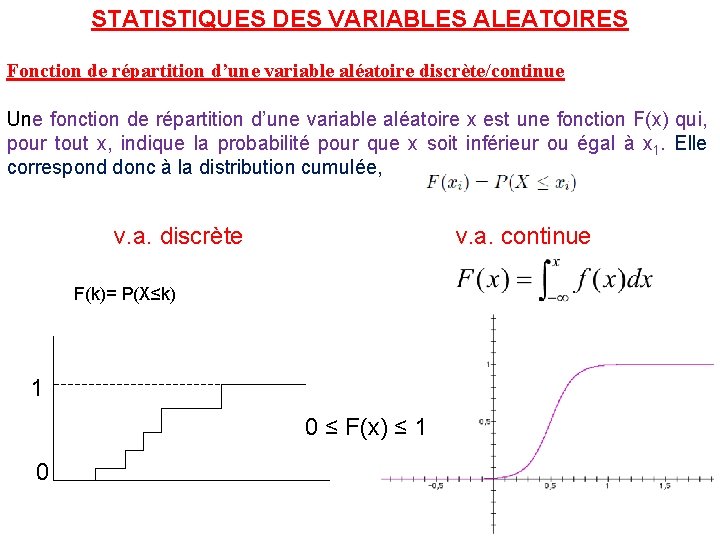
STATISTIQUES DES VARIABLES ALEATOIRES Fonction de répartition d’une variable aléatoire discrète/continue Une fonction de répartition d’une variable aléatoire x est une fonction F(x) qui, pour tout x, indique la probabilité pour que x soit inférieur ou égal à x 1. Elle correspond donc à la distribution cumulée, v. a. discrète v. a. continue F(k)= P(X≤k) 1 0 ≤ F(x) ≤ 1 0

STATISTIQUES DES VARIABLES ALEATOIRES ESPERANCE MATHEMATIQUE L’espérance, notée E(x) correspond à une moyenne pondérée Variable aléatoire discrète Soit X un va discrète qui prend des valeurs dans l'ensemble D et a comme densité de probabilité f(xi). Alors l’espérance mathématique ou moyenne statistique (ou d’ensemble) de X est: Variable aléatoire continue L’espérance mathématique (moyenne statistique) d'une va continue X avec une fonction de densité de probabilité (pdf) f (x) est:

STATISTIQUES DES VARIABLES ALEATOIRES VARIANCE La variance d'une variable aléatoire, notée Var(X) ou σ2, est une moyenne pondérée des écarts au carré de la moyenne. • Dans le cas discret, les poids sont donnés par la fonction de probabilité, • Dans le cas continu, les poids sont donnés par la fonction de densité de probabilité. L'écart type, noté σ, est la racine carrée positive de la variance. Étant donné que l'écart-type est mesuré dans les mêmes unités que la variable aléatoire et que la variance est mesurée en unités au carré, l'écart-type est souvent la mesure préférée. Variable aléatoire discrète Variable aléatoire continue

STATISTIQUES DES VARIABLES ALEATOIRES Exemple 1: Soit une source qui va émettre le mot suivant: Alphabet Source = le mot ‘’annaba’’={a, n, n, a, b, a} Les symboles générés par la source sont formés par 3 lettres de l’alphabet français à savoir a, n et b, mais pas avec la même loi de probabilité, si on se restreint à cet exemple basic. La loi de probabilité est donc (pour ce cas de figure) : P(‘’a’’)=1/2, P(‘’n’’)=1/3 et P(‘’b’’)=1/6 1 - Tracer sa densité de probabilité 2 - Sa fonction de répartition 3 - Calculer son espérance mathématique, sa variance et son écart type
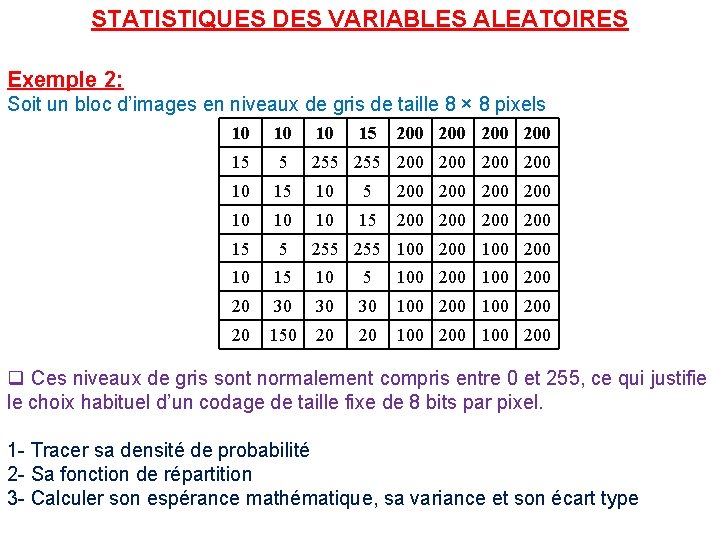
STATISTIQUES DES VARIABLES ALEATOIRES Exemple 2: Soit un bloc d’images en niveaux de gris de taille 8 × 8 pixels 10 10 10 15 200 200 15 5 255 200 200 10 15 10 5 200 200 10 10 10 15 200 200 15 5 255 100 200 10 15 100 200 20 30 30 30 100 200 20 150 20 20 100 200 q Ces niveaux de gris sont normalement compris entre 0 et 255, ce qui justifie le choix habituel d’un codage de taille fixe de 8 bits par pixel. 1 - Tracer sa densité de probabilité 2 - Sa fonction de répartition 3 - Calculer son espérance mathématique, sa variance et son écart type

STATISTIQUES DES VARIABLES ALEATOIRES Propriétés de l’espérance mathématique 1. Propriété de l’addition : E(X + Y) = E(X) + E(Y) Démonstration: 2. Propriété de mise à l'échelle (Multiplication par une constante) E(c. X) = c. E(X)

STATISTIQUES DES VARIABLES ALEATOIRES Propriétés de l’espérance mathématique 3. Propriété de linéarité : A partir des deux propriétés précédentes nous pouvons généraliser la propriété de linéarité de l’espérance mathématique 4. Inégalités de valeur absolue: 5. Multiplication E (XY) = E (X) E (Y). Ici, X et Y doivent être indépendants. 6. Addition à une constante E [X + a] = E [X] + a, où a est une constante

STATISTIQUES DES VARIABLES ALEATOIRES Propriétés de la variance 1. Propriété 1 2. Propriété 2: d’une manière générale nous avons 3. Propriété 3 : La variance d'une constante est de 0.

STATISTIQUES DES VARIABLES ALEATOIRES Propriétés de la variance 4. Propriété 4 V (a 1 X 1 + a 2 X 2 +… + an. Xn) = a 12 V (X 1) + a 22 V (X 2) +… + an 2 V (Xn). 1. Propriété 2: d’une manière générale nous avons 2. Propriété 3 : La variance d'une constante est de 0.

CAS DE DEUX VARIABLES ALEATOIRES DISCRETES Considérons d'abord le cas dans lequel deux variables aléatoires sont discrètes. C’est un cas très répondu surtout en télécommunications numériques où les données discrètes de l’émission et celles reçus, Nous allons donc étendre plusieurs des définitions que nous avons apprises pour une variable aléatoire discrète, telle que la fonction de masse de probabilité, la moyenne et la variance, au cas où nous ont deux variables aléatoires discrètes. Soit deux variables aléatoire X et Y chacune pouvant prendre une valeur dans un ensemble de 4 valeurs possibles équiprobables (même probabilité pour les 4 valeurs) : X = {1, 2, 3, 4} et Y = {1, 2, 3, 4} Commençons par trouver la «distribution de probabilité conjointe (x, y) désigne l'un des résultats possibles pour les deux variables simultanément.

CAS DE DEUX VARIABLES ALEATOIRES DISCRETES Si nous continuons à énumérer tous les résultats possibles, nous voyons bientôt que le l’ensemble de possibilités conjointes S a 16 résultats possibles: S = {(1, 1) ; (1, 2) ; (1, 3) ; (1, 4) ; (2, 1) ; (2, 2) ; (2, 3) ; (2, 4) ; (3, 1) ; (3, 2) ; (3, 3) ; (3, 4) ; (4, 1) ; (4, 2) ; (4, 3) ; (4, 4) } Comme X et Y sont équiprobables deux et statistiquement indépendante l’une de l’autre, nous devrions nous attendre à ce que chacun des 16 résultats possibles soit équiprobable. P(X=x, Y=y) = 1/16 La fonction de probabilité conjointe est généralement notée f (x, y), puisse être définie comme une formule, comme un graphique ou comme un tableau.

CAS DE DEUX VARIABLES ALEATOIRES DISCRETES Densité de probabilité Conjointe Soit X et Y deux variables aléatoires discrètes, et soit S désignent le support bidimensionnel de X et Y. Alors, la fonction f(x, y) = P(X=x, Y=y) est une fonction de masse de probabilité conjointe si elle satisfait les trois conditions suivantes:

CAS DE DEUX VARIABLES ALEATOIRES DISCRETES Densité de probabilité marginale Soit X une variable aléatoire discrète avec le support S 1, et soit Y une variable aléatoire discrète avec le support S 2. Soit X et Y la fonction de masse de probabilité conjointe avec le support S. Alors, la fonction de probabilité de la va X seule, appelée fonction de probabilité marginale de X, est définie par : De même, la fonction de probabilité de la va Y seule, appelée fonction de probabilité marginale de Y, est définie par :

CAS DE DEUX VARIABLES ALEATOIRES DISCRETES Indépendance et dépendance de 2 va Les variables aléatoires X et Y sont indépendantes si et seulement si: P(X=x, Y=y) = P(X=x) × P(Y=y) x S 1 et y S 2 Sinon, X et Y sont dits dépendants. Soit maintenant, une fonction de probabilité conjointe f (x, y), et que nous voulions trouver la moyenne statistique de X (notée E(X)). On peut commencer par trouver d'abord la densité de probabilité marginale de X, puis d'utiliser la définition de l’espérance E (X). Alternativement, nous pourrions utiliser la définition suivante de la moyenne. Où u(x, y) est fonction de ces deux variables aléatoires,

CAS DE DEUX VARIABLES ALEATOIRES DISCRETES Densité de probabilité conditionnelle Dans les pages précédentes de ce cours, nous sommes intéressés au comportement conjoint de deux variables aléatoires X et Y. Nous allons maintenant examiner comment l'une des deux variables aléatoires, disons Y, se comporte étant donné qu'une autre variable aléatoire, disons X, s'est déjà comportée d'une certaine manière. Fonction de masse de probabilité conditionnelle de X : La fonction de probabilité conditionnelle de X, étant donné que Y = y, est définie par: A condition que f. Y(y) > 0 Fonction de masse de probabilité conditionnelle de Y : La fonction de probabilité conditionnelle de Y, étant donné que X = x, est définie par: A condition que f. X(x) > 0

CAS DE DEUX VARIABLES ALEATOIRES DISCRETES Densité de probabilité conditionnelle Exemple: Soit X une variable aléatoire discrète avec support S 1 = {0, 1}, et soit Y une variable aléatoire discrète avec support S 2 = {0, 1, 2}. Supposons, sous forme tabulaire, que X et Y aient la distribution de probabilité conjointe suivante f(x, y): Quelle est la distribution conditionnelle de X sachant Y? Autrement dit, qu'est-ce que g (x / y)?

CAS DE DEUX VARIABLES ALEATOIRES DISCRETES Densité de probabilité conditionnelle Solution de l’exemple: En utilisant la formule suivante : A condition que f. Y(y) > 0

CAS DE DEUX VARIABLES ALEATOIRES DISCRETES Espérance et variance conditionnelles Supposons que X et Y sont des variables aléatoires discrètes. Alors, la moyenne conditionnelle de Y sachant X = x est définie comme: Et, la moyenne conditionnelle de X sachant Y = y est définie comme: La variance conditionnelle de Y sachant X = x: La variance conditionnelle de X sachant Y = y:

CAS DE DEUX VARIABLES ALEATOIRES CONTINUES Densité de probabilité Conjointe Soit X et Y deux variables aléatoires continues, et soit S désigne le support bidimensionnel de X et Y. Alors, la fonction f (x, y) est une fonction de densité de probabilité conjointe si elle satisfait les trois suivantes conditions: où {(X, Y) ∈ A} est un événement dans le plan xy Fonctions de densité de probabilité marginale Les fonctions de densité de probabilité marginale des variables aléatoires continues X et Y sont données respectivement par: où S 1 et S 2 sont les supports respectifs de X et Y.

CAS DE DEUX VARIABLES ALEATOIRES CONTINUES Densité de probabilité conditionnelle Fonction de masse de probabilité conditionnelle de X : La fonction de probabilité conditionnelle de X, étant donné que Y = y, est définie par: A condition que f. Y(y) > 0 Fonction de masse de probabilité conditionnelle de Y : La fonction de probabilité conditionnelle de Y, étant donné que X = x, est définie par: A condition que f. X(x) > 0

CAS DE DEUX VARIABLES ALEATOIRES CONTINUES Espérance et variance conditionnelles Supposons que X et Y sont des variables aléatoires continues. Alors, la moyenne conditionnelle de Y sachant X = x est définie comme: La variance conditionnelle de Y sachant X = x:
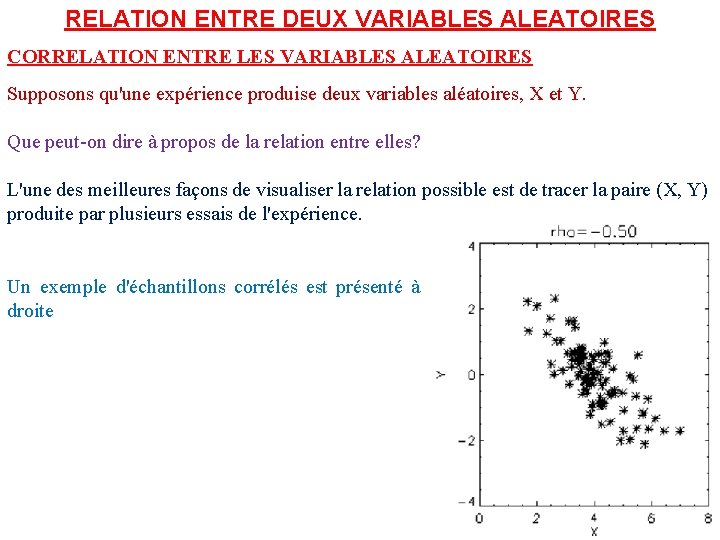
RELATION ENTRE DEUX VARIABLES ALEATOIRES CORRELATION ENTRE LES VARIABLES ALEATOIRES Supposons qu'une expérience produise deux variables aléatoires, X et Y. Que peut-on dire à propos de la relation entre elles? L'une des meilleures façons de visualiser la relation possible est de tracer la paire (X, Y) produite par plusieurs essais de l'expérience. Un exemple d'échantillons corrélés est présenté à droite
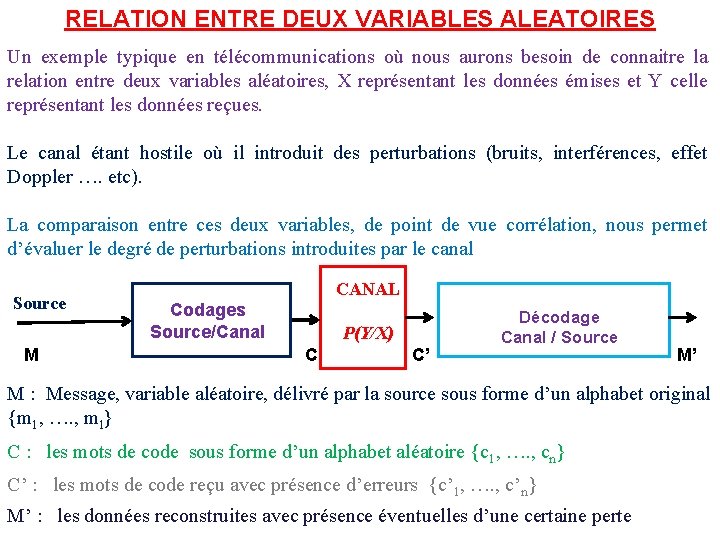
RELATION ENTRE DEUX VARIABLES ALEATOIRES Un exemple typique en télécommunications où nous aurons besoin de connaitre la relation entre deux variables aléatoires, X représentant les données émises et Y celle représentant les données reçues. Le canal étant hostile où il introduit des perturbations (bruits, interférences, effet Doppler …. etc). La comparaison entre ces deux variables, de point de vue corrélation, nous permet d’évaluer le degré de perturbations introduites par le canal Source M CANAL Codages Source/Canal P(Y/X) C C’ Décodage Canal / Source M’ M : Message, variable aléatoire, délivré par la source sous forme d’un alphabet original {m 1, …. , ml} C : les mots de code sous forme d’un alphabet aléatoire {c 1, …. , cn} C’ : les mots de code reçu avec présence d’erreurs {c’ 1, …. , c’n} M’ : les données reconstruites avec présence éventuelles d’une certaine perte

RELATION ENTRE DEUX VARIABLES ALEATOIRES FONCTION DE DENSITE CONJOINTE Le comportement conjoint de X et Y est entièrement capturé dans la distribution de probabilité conjointe. Pour une distribution continue • Cas de variables aléatoires continues • Cas de variables aléatoires discrètes

RELATION ENTRE DEUX VARIABLES ALEATOIRES FONCTION DE COVARIANCE ENTRE DEUX VARIABLES ALEATOIRES La fonction de covariance est un nombre qui mesure la variation commune de X et Y. Elle est définie comme : La covariance est déterminée par la différence entre : E [XY] et E [X] E [Y]. Si X et Y étaient statistiquement indépendants, alors E [XY] serait égal à E [X] E [Y] et la covariance serait nulle. La covariance d'une variable aléatoire avec elle-même est égale à sa variance. cov [X, X] = E [(X − E [X])2] = var [X]

RELATION ENTRE DEUX VARIABLES ALEATOIRES COEFFICIENT DE CORRELATION ENTRE DEUX VARIABLES ALEATOIRES La covariance peut être normalisée pour produire ce que l'on appelle le coefficient de corrélation, ρ. Le coefficient de corrélation est borné par − 1≤ρ≤ 1. Il aura la valeur ρ = 0 lorsque la covariance est nulle et la valeur ρ = ± 1 lorsque X et Y sont parfaitement corrélés ou anti-corrélés.

RELATION ENTRE DEUX VARIABLES ALEATOIRES COEFFICIENT DE CORRELATION ENTRE DEUX VARIABLES ALEATOIRES Exemple Soit une variable aléatoire X qui indique le nombre de tasses de chocolat chaud vendues quotidiennement dans un café local, et Y une variable aléatoire qui indique le nombre de muffins aux pommes et à la cannelle vendus quotidiennement dans le même café. Ensuite, le gérant du café pourrait bénéficier de savoir si X et Y sont fortement corrélés ou non. Si les variables aléatoires sont fortement corrélées, le gestionnaire saurait alors s'assurer que les deux sont disponibles un jour donné. Si les variables aléatoires ne sont pas fortement corrélées, alors le gestionnaire saurait qu'il serait normal que l'un des éléments soit disponible sans l'autre. Le coefficient de corrélation est la mesure statistique qui va nous permettre de quantifier le degré de corrélation entre deux variables aléatoires X et Y.

RELATION ENTRE DEUX VARIABLES ALEATOIRES COEFFICIENT DE CORRELATION ENTRE DEUX VARIABLES ALEATOIRES La fonction d'autocorrélation est très similaire à la fonction de covariance. En effet, elle permet de comparer deux variables aléatoires X et Y mais en tenant aussi compte de leurs moyennes statistiques (Espérance mathématique) ce qui fait la différence avec la fonction de covariance (qui elle compare uniquement les fluctuations des variables aléatoires sans leurs moyennes statistiques), Elle est définie comme : R (X, Y) = E [XY] = cov (X, Y) + E [X] E [Y] Elle conserve les valeurs moyennes dans le calcul de la valeur. Les variables aléatoires sont orthogonales si R (X, Y) = 0

RELATION ENTRE DEUX VARIABLES ALEATOIRES FONCTION DE CORRELATION ENTRE DEUX VARIABLES ALEATOIRES La fonction de corrélation est très similaire à la fonction de covariance. En effet, elle permet de comparer deux variables aléatoires X et Y mais en tenant aussi compte de leurs moyennes statistiques (Espérance mathématique) ce qui fait la différence avec la fonction de covariance (qui elle compare uniquement les fluctuations des variables aléatoires sans leurs moyennes statistiques), Elle est définie comme : R (X, Y) = E [XY] = cov (X, Y) + E [X] E [Y] Elle conserve les valeurs moyennes dans le calcul de la valeur. Les variables aléatoires sont orthogonales si R (X, Y) = 0
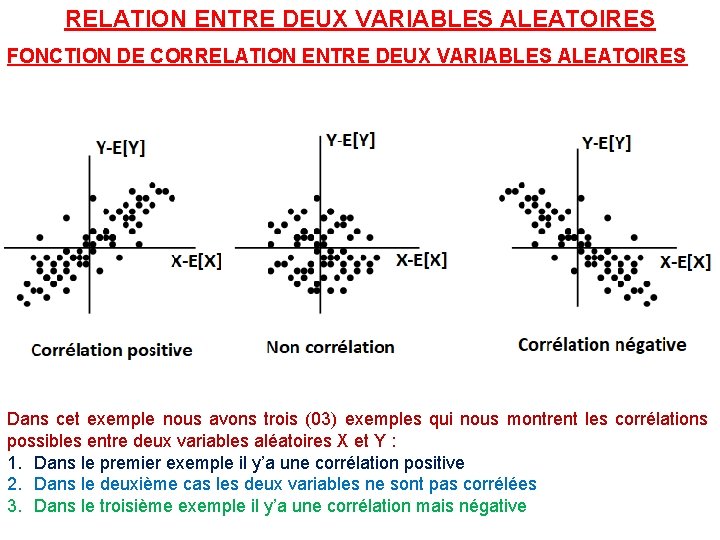
RELATION ENTRE DEUX VARIABLES ALEATOIRES FONCTION DE CORRELATION ENTRE DEUX VARIABLES ALEATOIRES Dans cet exemple nous avons trois (03) exemples qui nous montrent les corrélations possibles entre deux variables aléatoires X et Y : 1. Dans le premier exemple il y’a une corrélation positive 2. Dans le deuxième cas les deux variables ne sont pas corrélées 3. Dans le troisième exemple il y’a une corrélation mais négative
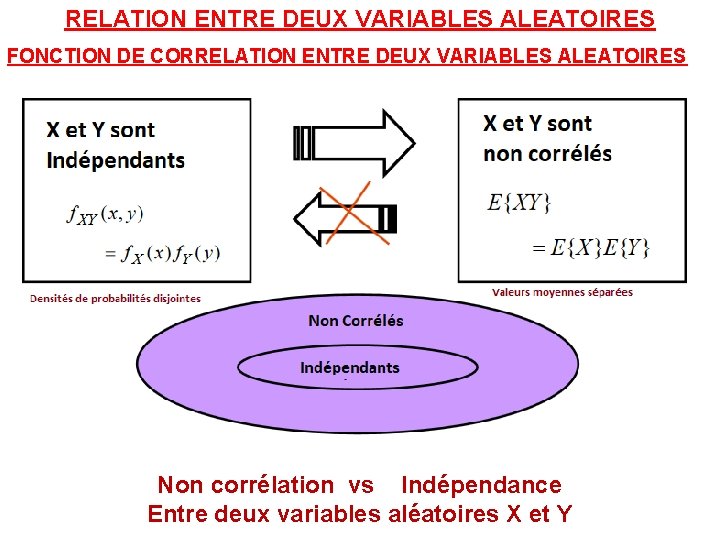
RELATION ENTRE DEUX VARIABLES ALEATOIRES FONCTION DE CORRELATION ENTRE DEUX VARIABLES ALEATOIRES Non corrélation vs Indépendance Entre deux variables aléatoires X et Y

RELATION ENTRE DEUX VARIABLES ALEATOIRES CORRELATION, COVARIANCE et COEFFICIENT DE CORRELATION

RELATION ENTRE DEUX VARIABLES ALEATOIRES INDEPENDANCE VS CORRELATION L'indépendance entre deux variables aléatoires (VA) X et Y, devrait être considérée comme disant qu’aucune des deux VA n'a un impact statistique sur l'autre Ainsi, les valeurs que l'un prendra probablement devraient être sans rapport avec la valeur que l'autre prendra.
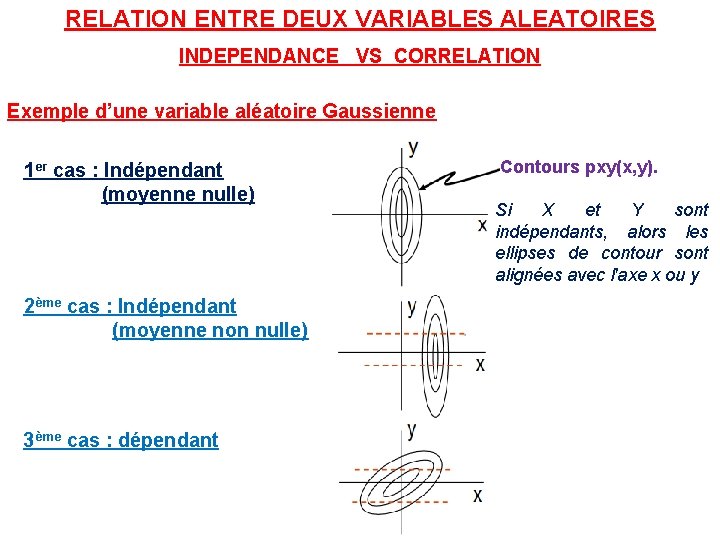
RELATION ENTRE DEUX VARIABLES ALEATOIRES INDEPENDANCE VS CORRELATION Exemple d’une variable aléatoire Gaussienne 1 er cas : Indépendant (moyenne nulle) 2ème cas : Indépendant (moyenne non nulle) 3ème cas : dépendant Contours pxy(x, y). Si X et Y sont indépendants, alors les ellipses de contour sont alignées avec l'axe x ou y

RELATION ENTRE DEUX VARIABLES ALEATOIRES INDEPENDANCE VS CORRELATION Deux variables aléatoires X et Y sont indépendantes si : Rappels : La fonction de Densité de probabilité décrit ‘’complètement’’ la variable aléatoire VR Mais souvent nous avons besoin aussi de : • L’espérance mathématique ou Moyenne d’ensemble, E[X], de la VA. Elle Décrit le centre de gravité de la densité de probabilité • Variance d’une VA qui décrit l’étalement ou propagation de la densité de probabilité • Corrélation d’une VA qui décrit un peu «l'inclinaison» de la densité de probabilité conjointe

RELATION ENTRE DEUX VARIABLES ALEATOIRES CORRELATION ET CONVARIANCE ENTRE N VARIABLES ALEATOIRES Dans ce cas nous pouvons parler d’un vecteur aléatoires Nous obtenons donc une matrice de corrélation, de N× N éléments, du vecteur x composé des N VA : Pareil pour la covariance qui devient alors une matrice de N× N éléments,

ENTROPIE D’UNE VARIABLE ALEATOIRE Comme nous venons de le voir, chaque variable aléatoire M={m 1, m 2, . . . . , m. K}, est régit par une probabilité d’apparition {P(m 1), P(m 2), . . . . , P(mk)}. Ceci, nous permet donc de définir les concepts de base de la théorie d’information à savoir : q L’information associée à chaque symbole de la source est : q L’entropie, qui représente la quantité d’information moyenne, d’une variable aléatoire M est donnée par: Comme nous pouvons le remarquer, cette quantité moyenne d’information d’une va, qui est l’entropie, dépend essentiellement de la loi de probabilité P.

ENTROPIE D’UNE VARIABLE ALEATOIRE q L’entropie, qui représentée la quantité d’information moyenne, d’une va M est donnée par: L’entropie d’une source représente donc la quantité d'information moyenne par caractère de la va. Elle représente aussi une incertitude moyenne par symbole. Elle peut exprimée en bit par symbole, c’est le cas de l’expression ci-dessus, si nous travaillons en base 2 (log 2). Plus l'entropie d’une variable aléatoire (va) est grande, plus il y’a de l’information délivrée par cette va et bien entendu l'incertitude est plus élevée. On montre que pour une loi de probabilité équiprobable ( m, P(mk)=p, et p=1) nous aurons une entropie maximale égale à :
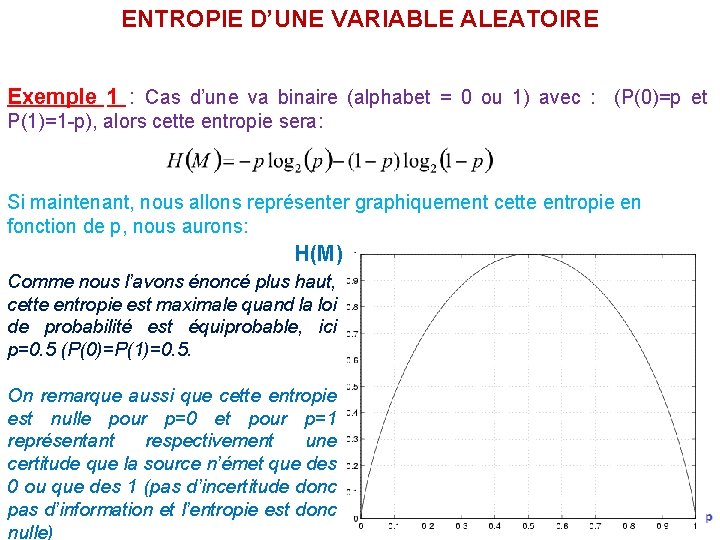
ENTROPIE D’UNE VARIABLE ALEATOIRE Exemple 1 : Cas d’une va binaire (alphabet = 0 ou 1) avec : (P(0)=p et P(1)=1 -p), alors cette entropie sera: Si maintenant, nous allons représenter graphiquement cette entropie en fonction de p, nous aurons: H(M) Comme nous l’avons énoncé plus haut, cette entropie est maximale quand la loi de probabilité est équiprobable, ici p=0. 5 (P(0)=P(1)=0. 5. On remarque aussi que cette entropie est nulle pour p=0 et pour p=1 représentant respectivement une certitude que la source n’émet que des 0 ou que des 1 (pas d’incertitude donc pas d’information et l’entropie est donc nulle)

ENTROPIE D’UNE VARIABLE ALEATOIRE Exemple 2 : Cas d’une va de k symboles {m 1, m 2, . . . . , m. K} équiprobables {P(m 1) = P(m 2) = , . . . . , = P(m. K) =1/K}, alors cette entropie sera: Evidemment, cette entropie est maximale pour cette source compte tenu que la loi de probabilité qui la régie est équiprobable. Dans le cas d’une loi quelconque régissant une source de K éléments nous avons:

REDONDANCE D’UNE VARIABLE ALEATOIRE Comme nous venons de le voir pour une va M de longueur K, l’entropie où quantité d’information moyenne délivrée par cette source est notée H(M). Elle est maximale pour une loi de probabilité équiprobable : On définit la redondance de la va comme étant l'écart ou la différence entre la valeur maximale possible (lorsque tous les symboles sont équiprobables) de son entropie et son entropie réelle. Une va dont l’entropie est faible est plus redondante. Autrement dit, il y’a moins d’incertitude et donc moins d’information délivrée par la va et par conséquence trop de redondance.

ENTROPIE MUTUELLE Supposons maintenant que nous avons deux va X et Y. Chacune possède alors une entropie que l’on définit par H(X) et H(Y). On définit : q I(X) et I(Y) : Information propre de X et de Y respectivement q. H(X, Y) : Information conjointe ou entropie mutuelle q. H(X/Y) : Informations partielle ou conditionnel de X sachant Y. Elle représente l’ambigüité ou l’incertitude qui reste sur X pour Y connu. q. H(Y/X) : Informations partielle ou conditionnel de Y sachant X. Elle représente l’ambigüité ou l’incertitude qui reste sur Y pour X connu. q. I(X, Y) : Information mutuelle ou quantité d’information de X réellement apportée par Y q I(X/Y) et I(Y/X) : Informations conditionnelles

ENTROPIE MUTUELLE q si X et Y sont deux variables aléatoires indépendantes, on a : H(X, Y) = H(X) + H(Y H(X/Y) = H(X) H(Y/X) = H(Y) I(X, Y) = I(X)-I(X/Y)=0 q Sinon, une certaine dépendance entre X et Y : H(X, Y) < H(X) + H(Y) < 2 H(X, Y) = H(X) + H(Y/X) H(X, Y) = H(Y) + H(X/Y) I(X, Y) = H(X) – H(X/Y) = H(Y) – H(Y/X) = H(X) + H(Y) – H(X, Y) > 0 I(X, Y) = I(X) – I(X/Y) > 0
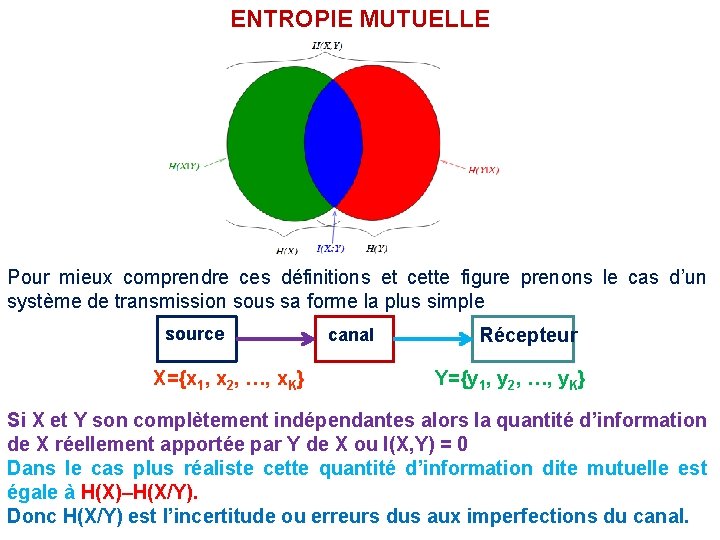
ENTROPIE MUTUELLE Pour mieux comprendre ces définitions et cette figure prenons le cas d’un système de transmission sous sa forme la plus simple source X={x 1, x 2, …, x. K} canal Récepteur Y={y 1, y 2, …, y. K} Si X et Y son complètement indépendantes alors la quantité d’information de X réellement apportée par Y de X ou I(X, Y) = 0 Dans le cas plus réaliste cette quantité d’information dite mutuelle est égale à H(X)–H(X/Y). Donc H(X/Y) est l’incertitude ou erreurs dus aux imperfections du canal.

ENTROPIE MUTUELLE

ENTROPIE MUTUELLE

ENTROPIE MUTUELLE

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Deux des distributions de probabilité discrètes les plus utilisées sont : • La loi de probabilité Binomiale • La loi de probabilité de Poisson. La fonction de probabilité binomiale (équation ci-dessous) fournit la probabilité que x succès se produiront dans n essais d'une expérience binomiale. Une variable Binomiale est donc une variable aléatoire X correspondant à la somme de n variables de Bernoulli. Notée X : B(n, p) Où X = nombre de succès au cours de n épreuves de Bernoulli identiques et indépendantes, 55

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Une expérience binomiale a quatre propriétés: (1) elle consiste en une séquence de n essais identiques; (2) deux résultats, succès ou échec, sont possibles pour chaque essai; (3) la probabilité de succès d'un essai, notée p, ne change pas d'un essai à l'autre; (4) les essais sont indépendants. Une famille qui a trois (03) enfant, La naissance de chaque enfant garçon ou fille a la même probabilité p=0, 5 3 enfant = n B(3, 0, 5) = 56

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Loi de probabilité d’une loi binomiale Fonction de répartition d’une loi binomiale Espérance mathématique d’une loi binomiale E(X) = np Variance d’une loi binomiale V(X) = np(1 -p) 57

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Exemple: Supposons que l'on sache que 10% des propriétaires d'automobiles de deux ans ont eu des problèmes avec le système électrique de leur automobile. Pour calculer la probabilité de trouver exactement 2 propriétaires qui ont eu des problèmes de système électrique sur un groupe de 10 propriétaires, la fonction de probabilité binomiale peut être utilisée en définissant n = 10, x = 2 et p = 0, 1 dans l'équation suivante; dans ce cas, la probabilité est de 0, 1937. 58

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Exemple: Un couple, tous deux porteurs d'une maladie récessive, souhaite avoir 5 enfants. Ils veulent connaître la probabilité qu'ils aient quatre enfants en bonne santé 59

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Exemple: Répartition du nombre de filles dans les fratries de 4 enfants, p: probabilité d’avoir une fille à chaque naissance = ½ X(Ω) = {0, 1, 2, 3, 4} X=0 X=1 X=2 X=3 X=4 Loi de probabilité B (4 ; 1/2) GGGG FGGG, GFGG, GGFG, GGGF FFGG, FGFG, FGGF, GFFG, GFGF, GGFF FFFG, FFGF, FGFF, GFFF FFFF q 4 4 q 3 p 6 q 2 p 2 4 qp 3 p 4 0. 0625 0. 375 0, 25 0, 0625 somme = 1 Indépendance statistique p (G G G G) = q. q = q 4 60

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Exemple: Une famille de n enfants, quelle est la probabilité d’avoir x garçons? B(2, 0. 5)= 0, 52 0, 50=0, 25 B(7, 0. 5)? 61

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Exemple: Avec n=2: B(2, 0. 5) x 0 1 2 P(x) 0. 25 62
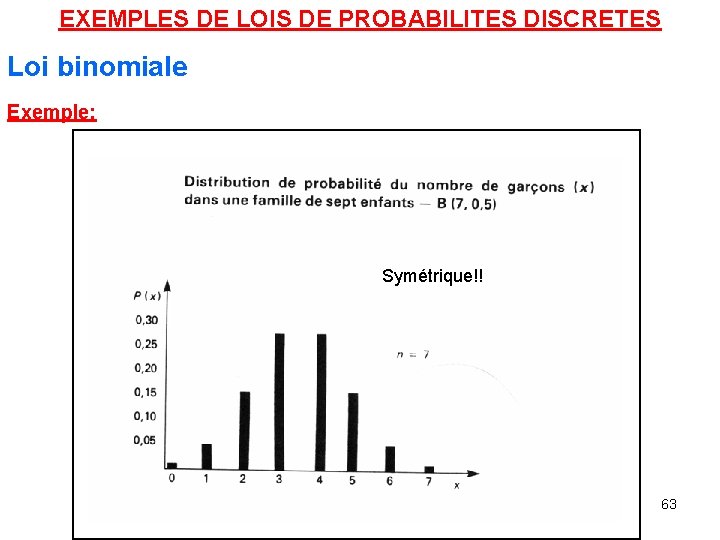
EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Exemple: Symétrique!! 63

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Exemple: Des rats sont conditionnés. Un passage a 25% d’être emprunté. 5 essais. . . B(5, 0. 25)? ? ? 64
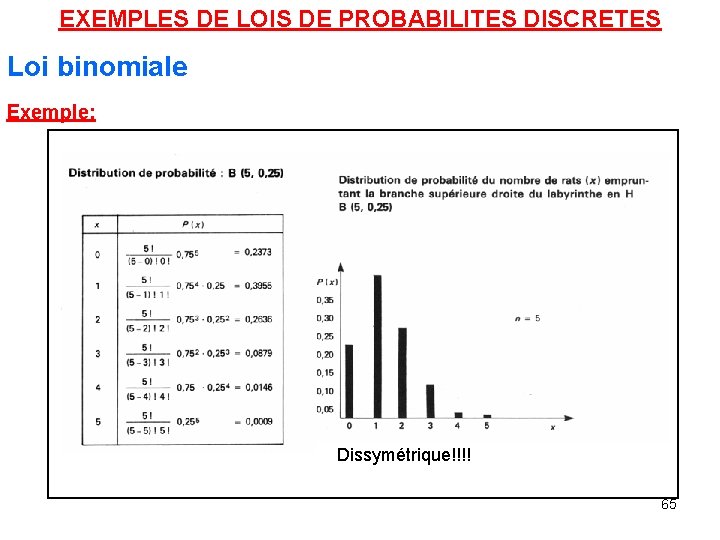
EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Exemple: Dissymétrique!!!! 65

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Espérance mathématique Pour la loi binomiale: Exemple: Quelle est l’espérance mathématique du nombre de garçons dans une famille de 7 enfants? 66

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi binomiale Pour une distribution binomiale: Exemple: Quelle est la variance du nombre de garçons dans une famille de 7 enfants? 67

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi de Poisson La distribution de probabilité de Poisson est souvent utilisée comme modèle du nombre d'arrivées dans une installation au cours d'une période donnée. Dans le cas d’une variable de Poisson, Poisson les événements se produisent les uns à la suite des autres, de façon aléatoire dans l’espace ou le temps. Loi de probabilité: Elle est appelée loi de Poisson, Poisson notée P(λ) E(X) = l k = 0, 1, 2, …, ∞ V(X) = l Exemple: une variable aléatoire pourrait être définie comme le nombre d'appels téléphoniques entrant dans un système de réservation d'une compagnie aérienne pendant une période de 15 minutes. Si le nombre moyen d'arrivées pendant un intervalle de 15 minutes est connu, la fonction de probabilité de Poisson donnée par l'équation ci-dessus peut être utilisée pour 68 calculer la probabilité de x arrivées.

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi de Poisson Exemple: une variable aléatoire pourrait être définie comme le nombre d'appels téléphoniques entrant dans un système de réservation d'une compagnie aérienne pendant une période de 15 minutes. Si le nombre moyen d'arrivées pendant un intervalle de 15 minutes est connu, la fonction de probabilité de Poisson donnée par l'équation ci-dessus peut être utilisée pour calculer la probabilité de x arrivées. Supposons que le nombre moyen d'appels arrivant dans une période de 15 minutes soit de 10. Pour calculer la probabilité que 5 appels arrivent dans les 15 minutes suivantes, μ = 10 et x = 5 sont substitués dans ci dessus, ce qui donne un probabilité de 0, 0378. Loi de probabilité: Elle est appelée loi de Poisson, Poisson notée P(λ) E(X) = l V(X) = l k = 0, 1, 2, …, ∞ 69

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi de Poisson La loi de Poisson: distribution théorique discontinue qui dérive de la loi binomiale. Une des éventualités a une probabilité très faible. Surtout utilisé lorsqu’on compte des individus ou des évènements distribués au hasard dans le temps ou dans l’espace. Loi binomiale tend vers Poisson si p diminue et n augmente. En pratique un événement est rare si p<0. 05. L’approximation est satisfaisante si n>50. 70

EXEMPLES DE LOIS DE PROBABILITES DISCRETES Loi de Poisson démontre que : Tend vers: Avantage: un seul paramètre (m) 71
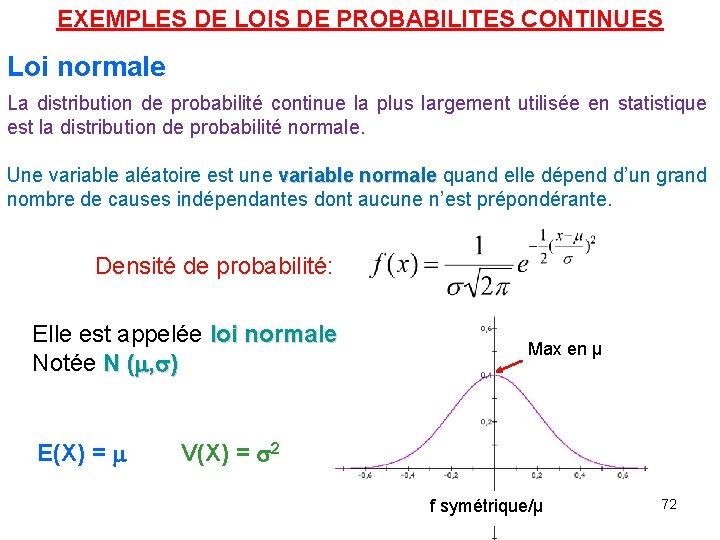
EXEMPLES DE LOIS DE PROBABILITES CONTINUES Loi normale La distribution de probabilité continue la plus largement utilisée en statistique est la distribution de probabilité normale. Une variable aléatoire est une variable normale quand elle dépend d’un grand nombre de causes indépendantes dont aucune n’est prépondérante. Densité de probabilité: Elle est appelée loi normale Notée N (m, s) E(X) = m Max en μ V(X) = s 2 f symétrique/μ 72
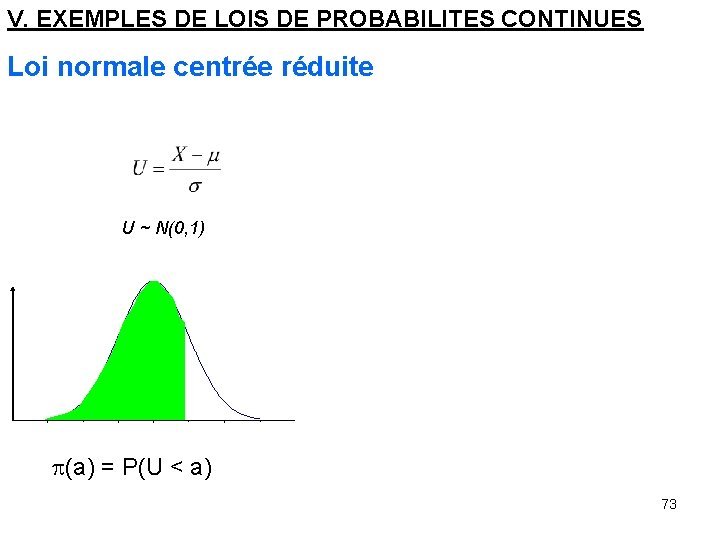
V. EXEMPLES DE LOIS DE PROBABILITES CONTINUES Loi normale centrée réduite U ~ N(0, 1) p(a) = P(U < a) 73
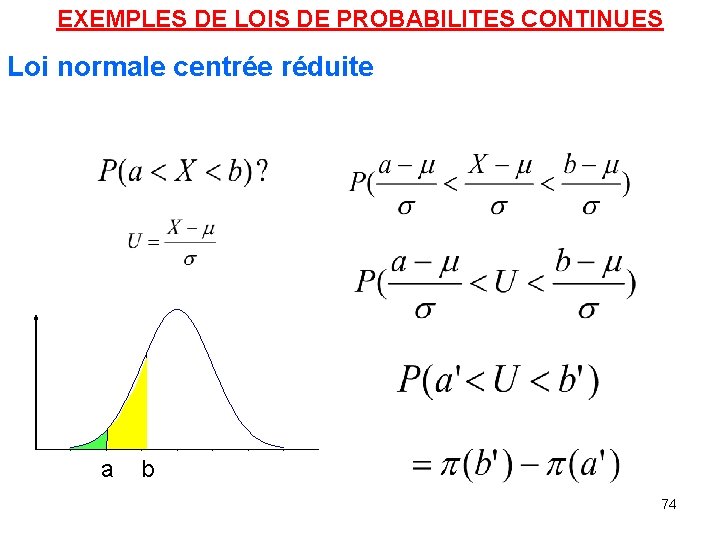
EXEMPLES DE LOIS DE PROBABILITES CONTINUES Loi normale centrée réduite a b 74

EXEMPLES DE LOIS DE PROBABILITES CONTINUES Loi normale centrée réduite ε ~ N(0, 1) a/2 -ea 1 -a a/2 0 ea 75

EXEMPLES DE LOIS DE PROBABILITES CONTINUES Loi du 2 de Pearson On appelle 2 à n degrés de liberté la variable aléatoire définie par : 76
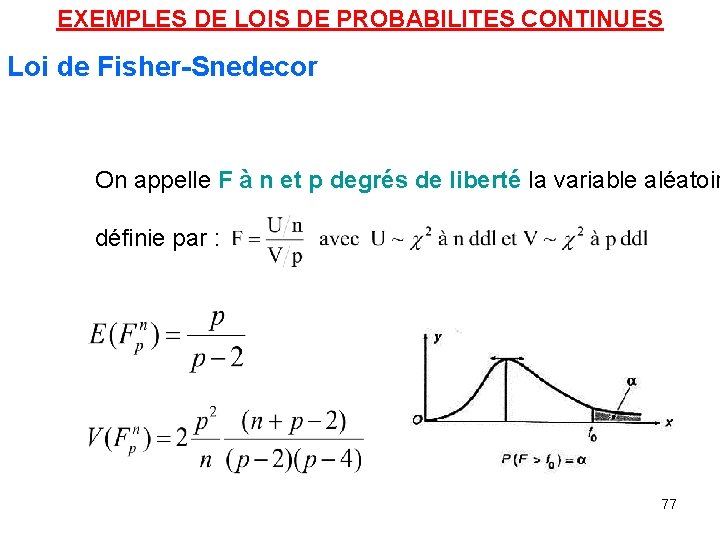
EXEMPLES DE LOIS DE PROBABILITES CONTINUES Loi de Fisher-Snedecor On appelle F à n et p degrés de liberté la variable aléatoir et définie par : 77

EXEMPLES DE LOIS DE PROBABILITES CONTINUES Loi de Student On appelle T à n degrés de liberté la variable aléatoire définie par : E(T) = 0 V(T) = n/n-2 78

EXEMPLES DE LOIS DE PROBABILITES CONTINUES Importance de la loi normale Théorème central limite de Laplace Toute somme de v. a. indépendantes de même loi est une variable asymptotiquement normale. En particulier: 79

EXEMPLES DE LOIS DE PROBABILITES CONTINUES Relations entre lois Lorsque n grand, p petit, np constant: B(n, p) -> P(l = np) Application du théorème centre limite Lorsque n est grand, la loi binomiale, la loi de Poisson, la loi de Student, la loi du χ 2, la loi de Fisher … tendent vers la loi normale 80

ESTIMATION Il est souvent intéressant de connaître les caractéristiques d'un grand groupe d'éléments tels que les individus, les ménages, les bâtiments, les produits, les pièces, les clients, etc. Tous les éléments d'intérêt dans une étude particulière forment la population. En raison du temps, du coût et d'autres considérations, les données ne peuvent souvent pas être collectées auprès de chaque élément de la population. Dans de tels cas, un sous-ensemble de la population, appelé échantillon, est utilisé pour fournir les données. Les données de l'échantillon sont ensuite utilisées pour élaborer des estimations des caractéristiques de l'ensemble de la population. Le processus consistant à utiliser un échantillon pour faire des inférences sur une population est appelé inférence statistique.

ESTIMATION Des caractéristiques telles que la moyenne de la population, la variance de la population et la proportion de la population sont appelées paramètres de la population. Les caractéristiques de l'échantillon telles que la moyenne de l'échantillon, la variance de l'échantillon et la proportion de l'échantillon sont appelées statistiques d'échantillon. Il existe deux types d'estimations: • le point • l'intervalle.

ESTIMATION Une estimation ponctuelle est une valeur d'une statistique d'échantillon qui est utilisée comme une estimation unique d'un paramètre de population. Aucune déclaration n'est faite sur la qualité ou la précision d'une estimation ponctuelle. Les statisticiens préfèrent les estimations d'intervalle parce que les estimations d'intervalle sont accompagnées d'un énoncé concernant le degré de confiance que l'intervalle contient le paramètre de population estimé. Les estimations d'intervalle des paramètres de population sont appelées intervalles de confiance.

ECHANTILLONNAGE ET DISTRIBUTION D’ECHANTILLONNAGE Les méthodes d'inférence statistique, et d'estimation en particulier, reposent sur la notion qu'un échantillon probabiliste a été prélevé. La principale caractéristique d'un échantillon probabiliste est que chaque élément de la population a une probabilité connue d'être inclus dans l'échantillon. Le type le plus fondamental est un simple échantillon aléatoire. Pour une population de taille N, un échantillon aléatoire simple est un échantillon sélectionné de telle sorte que chaque échantillon possible de taille n ait la même probabilité d'être sélectionné. Le fait de choisir les éléments de la population un par un afin que chaque élément ait la même probabilité d'être sélectionné fournira un échantillon aléatoire simple. Des tableaux de nombres aléatoires, ou des nombres aléatoires générés par ordinateur, peuvent être utilisés pour garantir que chaque élément a la même probabilité d'être sélectionné.

ECHANTILLONNAGE ET DISTRIBUTION D’ECHANTILLONNAGE Une distribution d'échantillonnage est une distribution de probabilité pour une statistique d'échantillon. La connaissance de la distribution d'échantillonnage est nécessaire pour construire une estimation d'intervalle pour un paramètre de population. C'est pourquoi un échantillon probabiliste est nécessaire; sans échantillon probabiliste, la distribution d'échantillonnage ne peut pas être déterminée et une estimation d'intervalle d'un paramètre ne peut pas être construite.

ESTIMATION D’UNE MOYENNE DE POPULATION Le processus d'estimation par points et intervalles le plus fondamental implique l'estimation d'une moyenne de population. Supposons qu'il soit intéressant d'estimer la moyenne de la population, μ, pour une variable quantitative. Les données collectées à partir d'un échantillon aléatoire simple peuvent être utilisées pour calculer la moyenne de l'échantillon, x , où la valeur de x fournit une estimation ponctuelle de μ. Lorsque la moyenne de l'échantillon est utilisée comme estimation ponctuelle de la moyenne de la population, on peut s'attendre à une certaine erreur en raison du fait qu'un échantillon, ou un sous-ensemble de la population, est utilisé pour calculer l'estimation ponctuelle. La valeur absolue de la différence entre la moyenne de l'échantillon, x , et la moyenne de la population, μ, écrite | x - μ |, est appelée erreur d'échantillonnage.

ESTIMATION D’UNE MOYENNE DE POPULATION L'estimation d'intervalle incorpore un énoncé de probabilité concernant l'ampleur de l'erreur d'échantillonnage. La distribution d'échantillonnage de x fournit la base d'une telle affirmation. Les statisticiens ont montré que la moyenne de la distribution d'échantillonnage de x est égale à la moyenne de la population, μ, et que l'écart type est donné par σ / Racine carrée de √n, où σ est l'écart-type de la population. L'écart type d'une distribution d'échantillonnage est appelé l'erreur standard. Pour les échantillons de grande taille, le théorème de la limite centrale indique la distribution d'échantillonnage de x peut être approximée par une distribution de probabilité normale. En pratique, les statisticiens considèrent généralement que les échantillons de taille 30 ou plus sont grands.

ESTIMATION D’UNE MOYENNE DE POPULATION L'estimation d'intervalle incorpore un énoncé de probabilité concernant l'ampleur de l'erreur d'échantillonnage. La distribution d'échantillonnage de x fournit la base d'une telle affirmation. Les statisticiens ont montré que la moyenne de la distribution d'échantillonnage de x est égale à la moyenne de la population, μ, et que l'écart type est donné par σ / Racine carrée de √n, où σ est l'écart-type de la population. L'écart type d'une distribution d'échantillonnage est appelé l'erreur standard. Pour les échantillons de grande taille, le théorème de la limite centrale indique la distribution d'échantillonnage de x peut être approximée par une distribution de probabilité normale. En pratique, les statisticiens considèrent généralement que les échantillons de taille 30 ou plus sont grands.

ESTIMATION D’UNE MOYENNE DE POPULATION Dans le cas du grand échantillon, une estimation de l'intervalle de confiance à 95% pour la moyenne de la population est donnée par x ± 1, 96σ / Racine carrée de √n. Lorsque l'écart type de la population, σ, est inconnu, l'écart type de l'échantillon est utilisé pour estimer σ dans la formule d'intervalle de confiance. La quantité 1, 96σ / Racine carrée de √n est souvent appelée marge d'erreur pour l'estimation. La quantité σ / Racine carrée de √n est l'erreur standard, et 1, 96 est le nombre d'erreurs standard à partir de la moyenne nécessaire pour inclure 95% des valeurs dans une distribution normale. L'interprétation d'un intervalle de confiance à 95% est que 95% des intervalles construits de cette manière contiendront la moyenne de la population. Ainsi, tout intervalle calculé de cette manière a une confiance de 95% pour contenir la moyenne de la population.

ESTIMATION D’UNE MOYENNE DE POPULATION En changeant la constante de 1, 96 à 1, 645, un intervalle de confiance de 90% peut être obtenu. Il convient de noter à partir de la formule pour une estimation d'intervalle qu'un intervalle de confiance à 90% est plus étroit qu'un intervalle de confiance à 95% et, en tant que tel, a un degré de confiance légèrement plus faible d'inclusion de la moyenne de la population. Des niveaux de confiance plus faibles conduisent à des intervalles encore plus étroits. En pratique, un intervalle de confiance de 95% est le plus utilisé. En raison de la présence du terme n 1 / 2 dans la formule pour une estimation d'intervalle, la taille de l'échantillon affecte la marge d'erreur. Des échantillons de plus grande taille entraînent de plus petites marges d'erreur. Cette observation constitue la base des procédures utilisées pour sélectionner la taille de l'échantillon. Les tailles d'échantillon peuvent être choisies de telle sorte que l'intervalle de confiance satisfasse toutes les exigences souhaitées concernant la taille de la marge d'erreur.

ESTIMATION D’UNE MOYENNE DE POPULATION La procédure que nous venons de décrire pour élaborer des estimations d'intervalle d'une moyenne de population est basée sur l'utilisation d'un grand échantillon. Dans le cas du petit échantillon, c'est-à-dire où la taille de l'échantillon n est inférieure à 30, la distribution t est utilisée pour spécifier la marge d'erreur et construire une estimation de l'intervalle de confiance. Par exemple, à un niveau de confiance de 95%, une valeur de la distribution t, déterminée par la valeur de n, remplacerait la valeur de 1, 96 obtenue à partir de la distribution normale. Les valeurs t seront toujours plus grandes, conduisant à des intervalles de confiance plus larges, mais, à mesure que la taille de l'échantillon devient plus grande, les valeurs t se rapprochent des valeurs correspondantes d'une distribution normale. Avec une taille d'échantillon de 25, la valeur t utilisée serait de 2, 064, par rapport à la valeur de distribution de probabilité normale de 1, 96 dans le cas du grand échantillon.

ESTIMATION D’UNE MOYENNE DE POPULATION Les procédures d'estimation peuvent être étendues à deux populations pour des études comparatives. Par exemple, supposons qu'une étude soit menée pour déterminer les différences entre les salaires versés à une population d'hommes et à une population de femmes. Deux échantillons aléatoires simples indépendants, l'un de la population d'hommes et l'autre de la population de femmes, fourniraient deux moyennes d'échantillonnage, x 1 et x 2. La différence entre les deux moyennes d'échantillonnage, x 1 - x 2, serait utilisée comme une estimation ponctuelle de la différence entre les deux moyennes de population. La distribution d'échantillonnage de x 1 - x 2 fournirait la base d'une estimation d'intervalle de confiance de la différence entre les deux moyennes de population. Pour les variables qualitatives, les estimations ponctuelles et d'intervalle de la différence entre les proportions de population peuvent être construites en considérant la différence entre les proportions de l'échantillon.

TESTS D’HYPOTHESES Le test d'hypothèse est une forme d'inférence statistique qui utilise les données d'un échantillon pour tirer des conclusions sur un paramètre de population ou une distribution de probabilité de population. Tout d'abord, une hypothèse provisoire est faite sur le paramètre ou la distribution. Cette hypothèse est appelée hypothèse nulle et est notée H 0. Une hypothèse alternative (notée Ha), qui est l'opposé de ce qui est énoncé dans l'hypothèse nulle, est alors définie. La procédure de test d'hypothèse consiste à utiliser des échantillons de données pour déterminer si H 0 peut être rejeté ou non. Si H 0 est rejeté, la conclusion statistique est que l'hypothèse alternative Ha est vraie.

TESTS D’HYPOTHESES Par exemple, supposons qu'une station de radio sélectionne la musique qu'elle joue en partant de l'hypothèse que l'âge moyen de son auditoire est de 30 ans. Pour déterminer si cette hypothèse est valide, un test d'hypothèse pourrait être conduit avec l'hypothèse nulle donnée comme H 0: μ = 30 et l'hypothèse alternative donnée comme Ha: μ ≠ 30. Sur la base d'un échantillon d'individus du public d'écoute, l'échantillon l'âge moyen, x , peut être calculé et utilisé pour déterminer s'il existe des preuves statistiques suffisantes pour rejeter H 0. Sur le plan conceptuel, une valeur de la moyenne de l'échantillon qui est «proche» de 30 est cohérente avec l'hypothèse nulle, tandis qu'une valeur de la moyenne de l'échantillon qui n'est «pas proche» de 30 étaye l'hypothèse alternative. Ce qui est considéré comme «proche» et «pas proche» est déterminé en utilisant la distribution d'échantillonnage de x. Idéalement, la procédure de test d'hypothèse conduit à l'acceptation de H 0 lorsque H 0 est vrai et au rejet de H 0 lorsque H 0 est faux.

TESTS D’HYPOTHESES Malheureusement, comme les tests d'hypothèse sont basés sur des informations d'échantillons, la possibilité d'erreurs doit être considérée. Une erreur de type I correspond au rejet de H 0 lorsque H 0 est réellement vrai, et une erreur de type II correspond à l'acceptation de H 0 lorsque H 0 est faux. La probabilité de faire une erreur de type I est notée α et la probabilité de faire une erreur de type II est notée β. En utilisant la procédure de test d'hypothèse pour déterminer si l'hypothèse nulle doit être rejetée, la personne effectuant le test d'hypothèse spécifie la probabilité maximale admissible de commettre une erreur de type I, appelée niveau de signification du test. Les choix courants pour le niveau de signification sont α = 0, 05 et α = 0, 01. Bien que la plupart des applications de test d'hypothèse contrôlent la probabilité de commettre une erreur de type I, elles ne contrôlent pas toujours la probabilité de commettre une erreur de type II.

TESTS D’HYPOTHESES Un graphique appelé courbe caractéristique de fonctionnement peut être construit pour montrer comment les changements dans la taille de l'échantillon affectent la probabilité de commettre une erreur de type II. Un concept connu sous le nom de valeur p fournit une base pratique pour tirer des conclusions dans les applications de test d'hypothèses. La valeur p est une mesure de la probabilité des résultats de l'échantillon, en supposant que l'hypothèse nulle est vraie; plus la valeur p est petite, moins les résultats de l'échantillon sont probables. Si la valeur p est inférieure à α, l'hypothèse nulle peut être rejetée; sinon, l'hypothèse nulle ne peut être rejetée. La valeur p est souvent appelée le niveau de signification observé pour le test. Un test d'hypothèse peut être effectué sur les paramètres d'une ou plusieurs populations ainsi que dans diverses autres situations. Dans chaque cas, le processus commence par la formulation d'hypothèses nulles et alternatives sur la population.

TESTS D’HYPOTHESES En plus de la moyenne de la population, des procédures de test d'hypothèses sont disponibles pour les paramètres de population tels que les proportions, les variances, les écarts types et les médianes. Des tests d'hypothèse sont également effectués dans l'analyse de régression et de corrélation pour déterminer si la relation de régression et le coefficient de corrélation sont statistiquement significatifs (voir ci-dessous Analyse de régression et de corrélation). Un test d'ajustement fait référence à un test d'hypothèse dans lequel l'hypothèse nulle est que la population a une distribution de probabilité spécifique, telle qu'une distribution de probabilité normale. Les méthodes statistiques non paramétriques impliquent également une variété de procédures de test d'hypothèses.

METHODES BAYESIENNES Les méthodes d'inférence statistique décrites précédemment souvent appelées méthodes classiques. Les méthodes bayésiennes (ainsi appelées d'après le mathématicien anglais Thomas Bayes) fournissent des alternatives qui permettent de combiner des informations antérieures sur un paramètre de population avec des informations contenues dans un échantillon pour guider le processus d'inférence statistique. Une distribution de probabilité préalable pour un paramètre d'intérêt est spécifiée en premier. Les informations de l'échantillon sont ensuite obtenues et combinées par une application du théorème de Bayes pour fournir une distribution de probabilité postérieure pour le paramètre. La distribution postérieure fournit la base des inférences statistiques concernant le paramètre. Une caractéristique clé, et quelque peu controversée, des méthodes bayésiennes est la notion de distribution de probabilité pour un paramètre de population.

METHODES BAYESIENNES Selon les statistiques classiques, les paramètres sont des constantes et ne peuvent pas être représentés comme des variables aléatoires. Les partisans bayésiens soutiennent que, si une valeur de paramètre est inconnue, il est alors logique de spécifier une distribution de probabilité qui décrit les valeurs possibles du paramètre ainsi que leur probabilité. L'approche bayésienne permet d'utiliser des données objectives ou une opinion subjective pour spécifier une distribution a priori. Avec l'approche bayésienne, différents individus peuvent spécifier différentes distributions antérieures. Les statisticiens classiques affirment que pour cette raison, les méthodes bayésiennes souffrent d'un manque d'objectivité. Les partisans bayésiens soutiennent que les méthodes classiques d'inférence statistique ont une subjectivité intégrée (par le choix d'un plan d'échantillonnage) et que l'avantage de l'approche bayésienne est que la subjectivité est rendue explicite.

METHODES BAYESIENNES Les méthodes bayésiennes ont été largement utilisées dans la théorie de la décision statistique. Dans ce contexte, le théorème de Bayes fournit un mécanisme pour combiner une distribution de probabilité a priori pour les états de la nature avec des informations d’échantillon pour fournir une distribution de probabilité révisée (postérieure) sur les états de la nature. Ces probabilités postérieures sont ensuite utilisées pour prendre de meilleures décisions.
- Slides: 100