Les triangles isomtriques les proprits Des triangles isomtriques

Les triangles isométriques ~ =

les propriétés Des triangles isométriques: - mêmes mesures d’angles homologues; - mêmes mesures de côtés homologues; - mêmes périmètres et mêmes aires; - le rapport des lignes homologues est égal à 1; - elles sont donc parfaitement superposables.

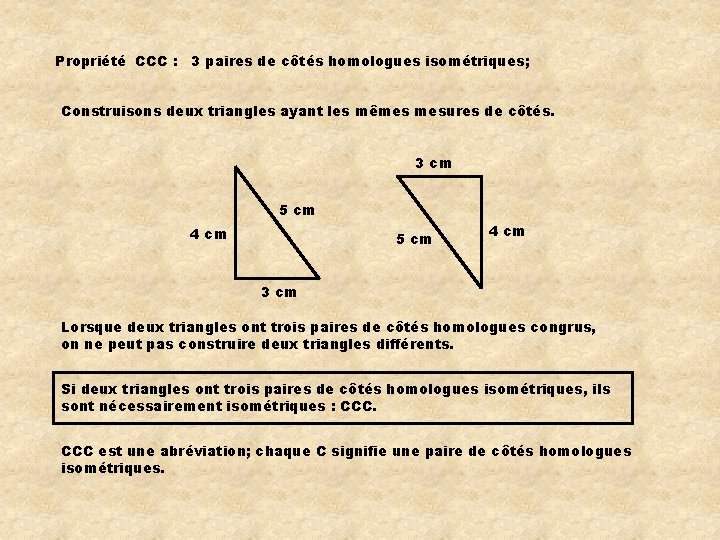
Propriété CCC : 3 paires de côtés homologues isométriques; Construisons deux triangles ayant les mêmes mesures de côtés. 3 cm 5 cm 4 cm 3 cm Lorsque deux triangles ont trois paires de côtés homologues congrus, on ne peut pas construire deux triangles différents. Si deux triangles ont trois paires de côtés homologues isométriques, ils sont nécessairement isométriques : CCC est une abréviation; chaque C signifie une paire de côtés homologues isométriques.

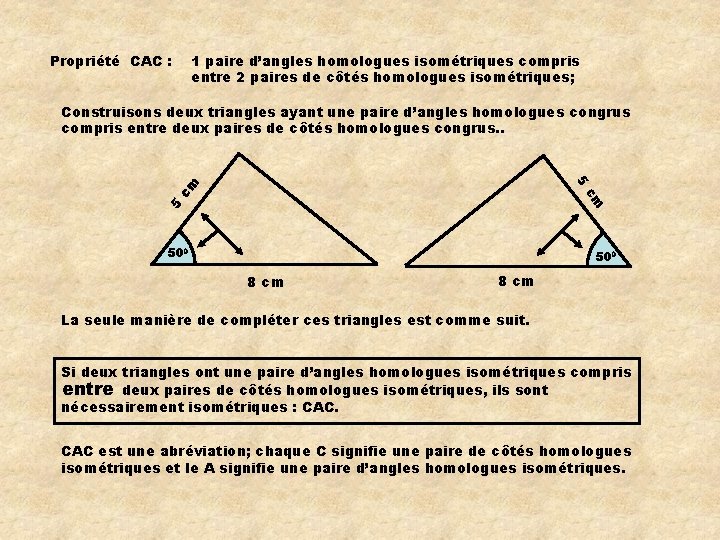
Propriété CAC : 1 paire d’angles homologues isométriques compris entre 2 paires de côtés homologues isométriques; Construisons deux triangles ayant une paire d’angles homologues congrus compris entre deux paires de côtés homologues congrus. . 5 cm cm 5 500 8 cm La seule manière de compléter ces triangles est comme suit. Si deux triangles ont une paire d’angles homologues isométriques compris entre deux paires de côtés homologues isométriques, ils sont nécessairement isométriques : CAC est une abréviation; chaque C signifie une paire de côtés homologues isométriques et le A signifie une paire d’angles homologues isométriques.

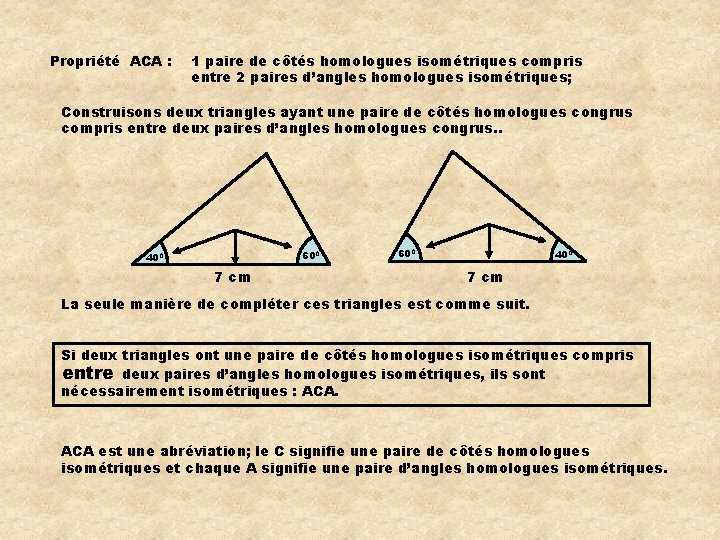
Propriété ACA : 1 paire de côtés homologues isométriques compris entre 2 paires d’angles homologues isométriques; Construisons deux triangles ayant une paire de côtés homologues congrus compris entre deux paires d’angles homologues congrus. . 600 400 7 cm La seule manière de compléter ces triangles est comme suit. Si deux triangles ont une paire de côtés homologues isométriques compris entre deux paires d’angles homologues isométriques, ils sont nécessairement isométriques : ACA est une abréviation; le C signifie une paire de côtés homologues isométriques et chaque A signifie une paire d’angles homologues isométriques.

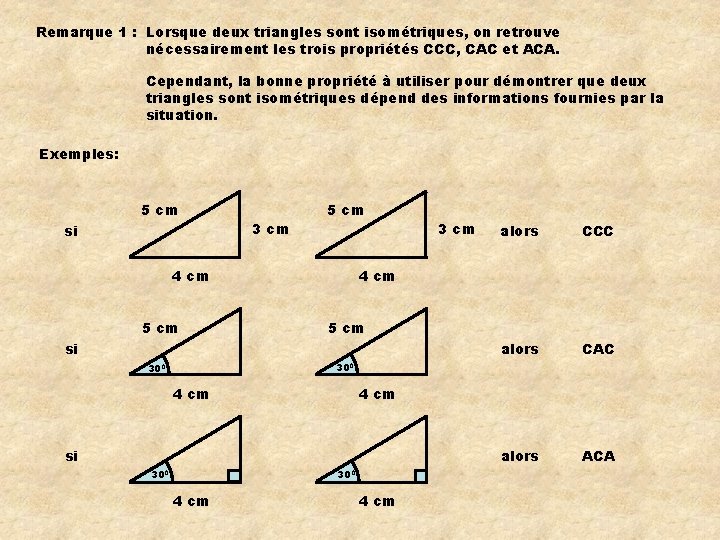
Remarque 1 : Lorsque deux triangles sont isométriques, on retrouve nécessairement les trois propriétés CCC, CAC et ACA. Cependant, la bonne propriété à utiliser pour démontrer que deux triangles sont isométriques dépend des informations fournies par la situation. Exemples: 5 cm si 3 cm 5 cm 4 cm 5 cm 3 cm alors CCC alors CAC alors ACA 4 cm 5 cm si 300 300 4 cm

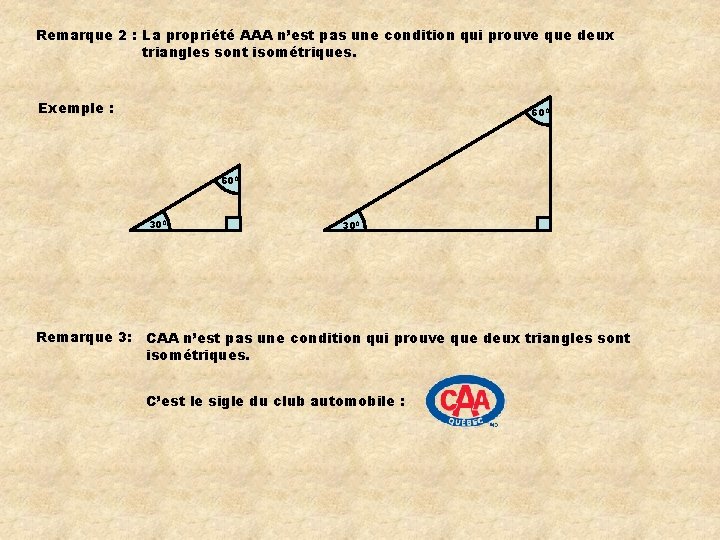
Remarque 2 : La propriété AAA n’est pas une condition qui prouve que deux triangles sont isométriques. Exemple : 600 300 Remarque 3: 300 CAA n’est pas une condition qui prouve que deux triangles sont isométriques. C’est le sigle du club automobile :

Voyons Démontrer maintenant que : quelques applications. B A Toute diagonale d’un parallélogramme engendre deux triangles isométriques. D Affirmations 1) AD ~ = BC et AB ~ = DC 2) AC ~ = AC 3) ∆ ABC ~ = Justifications 1) Les côtés opposés d’un parallélogramme sont isométriques. 2) Car AC est un côté commun aux deux triangles. ∆ ADC C 3) CCC

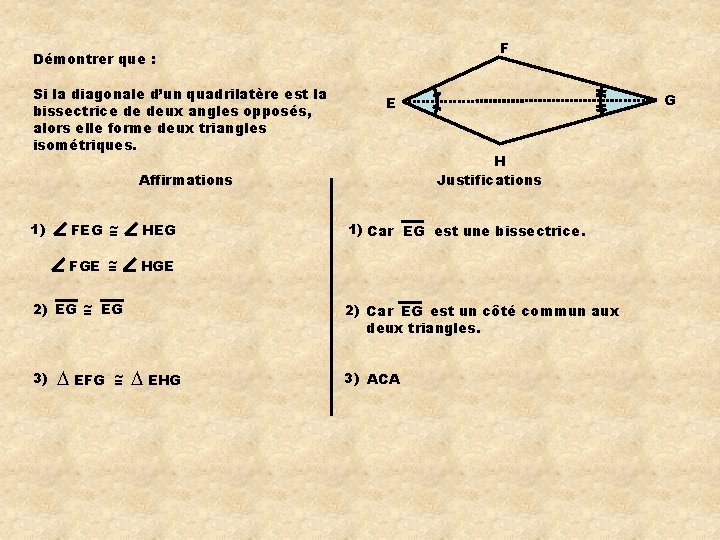
F Démontrer que : Si la diagonale d’un quadrilatère est la bissectrice de deux angles opposés, alors elle forme deux triangles isométriques. H Justifications Affirmations 1) FEG ~ = HEG FGE ~ = HGE 2) EG ~ = EG 3) ∆ EFG ~ = G E 1) Car EG est une bissectrice. 2) Car EG est un côté commun aux deux triangles. ∆ EHG 3) ACA

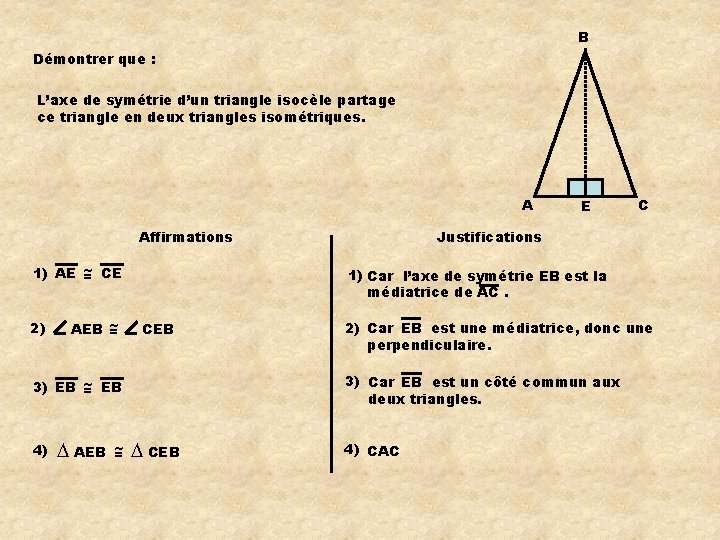
B Démontrer que : L’axe de symétrie d’un triangle isocèle partage ce triangle en deux triangles isométriques. A Affirmations 1) AE ~ = CE 2) AEB ~ = ∆ AEB ~ = C Justifications 1) Car l’axe de symétrie EB est la médiatrice de AC. CEB 2) Car EB est une médiatrice, donc une perpendiculaire. 3) Car EB est un côté commun aux deux triangles. 3) EB ~ = EB 4) E ∆ CEB 4) CAC

B A Démontrer que : Les angles opposés d’un parallélogramme sont congrus. D Affirmations 1) AD ~ = BC et AB ~ = DC 2) AC ~ = AC 3) ∆ ABC 4) B ~ = C Justifications 1) Les côtés opposés d’un parallélogramme sont isométriques. 2) Car AC est un côté commun aux deux triangles. ∆ ADC 3) CCC D 4) Dans les triangles isométriques, les éléments homologues sont congrus. Remarque: Après avoir démontré que deux triangles sont isométriques, cet axiome peut être utilisé pour justifier une affirmation.

A Démontrer que : B Dans un cercle, deux angles au centre congrus déterminent des cordes congrus. Affirmations 1) AO ~ = BO ~ = CO ~ = DO 2) 3) AOB ~ = ∆ AOB ~ = COD ∆ COD 4) AB ~ = CD O Justifications C D 1) Les rayons d’un même cercle sont congrus. 2) C’est une donnée du problème. 3) CAC 4) Dans les triangles isométriques, les éléments homologues sont congrus.

Dans cette figure : ~ DH FD = FE Démontrer que : F GH ~ GH FE = E Affirmations G D Justifications 1) ~ FDE = GDH 1) Ce sont des angles opposés par le sommet. 2) ~ DFE = GHD 2) Ce sont des angles alternes-internes formés par des parallèles. ~ DH 3) FD = 4) ∆ FED ~ = ∆ GDH ~ GH 5) FE = 3) C’est une donnée du problème. 4) ACA 5) Dans les triangles isométriques, les éléments homologues sont congrus. H

D Dans cette figure : AE et BD se coupent en leur milieu. A 2 cm 3, 1 cm 400 C 450 2 cm 3, 1 cm B A) Détermine la mesure de l’angle B en donnant l’énoncé qui justifie ton calcul. m B = 950 ; la somme des mesures des angles intérieurs d’un triangle = 180 0. B) En vertu de quel énoncé, les deux triangles sont-ils isométriques ? ~ CE et BC = ~ CD ; c’est une donnée du problème. CAC car AC = et C) Détermine m m ~ ACB = DCE ; angles opposés par le sommet. D et donne l’énoncé qui justifie ta réponse. D = 950 ; dans les triangles isométriques, les éléments homologues sont congrus. E