Les quations de la rgression logistique Deux variables

Les équations de la régression logistique – Deux variables indépendantes dichotomiques n Le tableau s’écrit alors X 1 X 2 11 01 10 00 X 1=1 ; X 2=1 X 1=0 ; X 2=1 X 1=1 ; X 2=0 X 1=0 ; X 2=0 Y=1 A C E G Y=0 B D F H Total A+C C+D E+F G+H

Deux variables indépendantes dichotomiques X 1 X 2 11 01 10 00 X 1=1 X 2=1 X 1=0 X 2=1 X 1=1 X 2=0 X 1=0 X 2=0 Y=1 A C E G Y=0 B D F H Total A+C C+D E+F G+H Ici la référence est X 1=0 et X 2=0 L’équation n Avec

Deux variables indépendantes dichotomiques X 1 X 2 11 01 10 00 X 1=1 X 2=1 X 1=0 X 2=1 X 1=1 X 2=0 X 1=0 X 2=0 Y=1 A C E G Y=0 B D F H Total A+C C+D E+F G+H Ici la référence est X 1=0 et X 2=0 L’équation

Deux variables indépendantes dichotomiques X 1 X 2 11 01 10 00 X 1=1 X 2=1 X 1=0 X 2=1 X 1=1 X 2=0 X 1=0 X 2=0 Y=1 a 1 b 1 a 0 b 0 Y=0 c 1 d 1 c 0 d 0 Total n 11 n 01 n 10 n 00 Ici la référence est X 1=0 et X 2=0 L’équation

INTRODUCTION DE LA MESURE DE L’INTERACTION X 1 X 2 11 01 10 00 X 1=1 X 2=1 X 1=0 X 2=1 X 1=1 X 2=0 X 1=0 X 2=0 Y=1 A C E G Y=0 B D F H Total A+C C+D E+F G+H Ici la référence est X 1=0 et X 2=0 L’équation n Avec

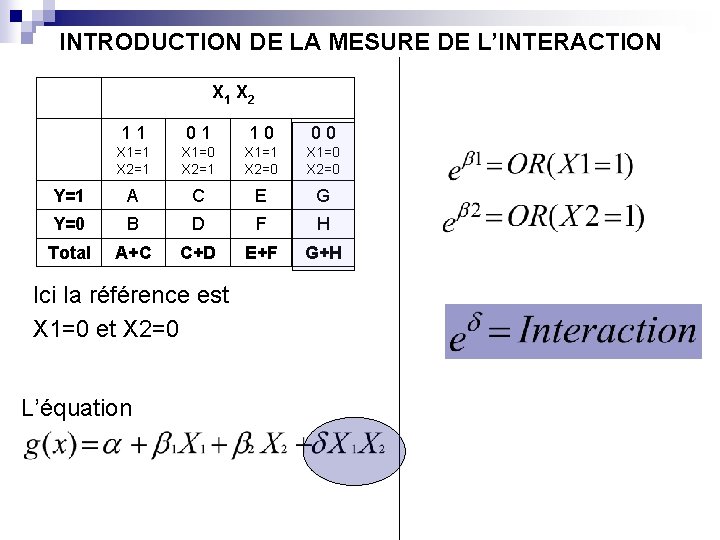
INTRODUCTION DE LA MESURE DE L’INTERACTION X 1 X 2 11 01 10 00 X 1=1 X 2=1 X 1=0 X 2=1 X 1=1 X 2=0 X 1=0 X 2=0 Y=1 A C E G Y=0 B D F H Total A+C C+D E+F G+H Ici la référence est X 1=0 et X 2=0 L’équation

INTRODUCTION DE LA MESURE DE L’INTERACTION X 1 X 2 11 01 10 00 X 1=1 X 2=1 X 1=0 X 2=1 X 1=1 X 2=0 X 1=0 X 2=0 Y=1 A C E G Y=0 B D F H Total A+C C+D E+F G+H Ici la référence est X 1=0 et X 2=0 L’équation

Application numérique (exemple 2. 2 du site) source : http: //www. uquebec. ca/ n Soit un échantillon de 7000 naissances. On cherche à expliquer une variable : ¨ ¨ ¨ X 1 X 2 Y « peser (=1) ou ne pas peser (Y=0) moins de 2500 grammes à la naissance » par deux variables dichotomique X 1 : être (X 1=1) fumeuse ou ne pas être fumeuse (X 1=0) X 2 : avoir (X 2=1) ou non (X 2=0) des antécédents de prématurité 11 01 10 00 Y=1 100 50 50 50 Y=0 475 2320 3480 Total 575 525 2370 3530

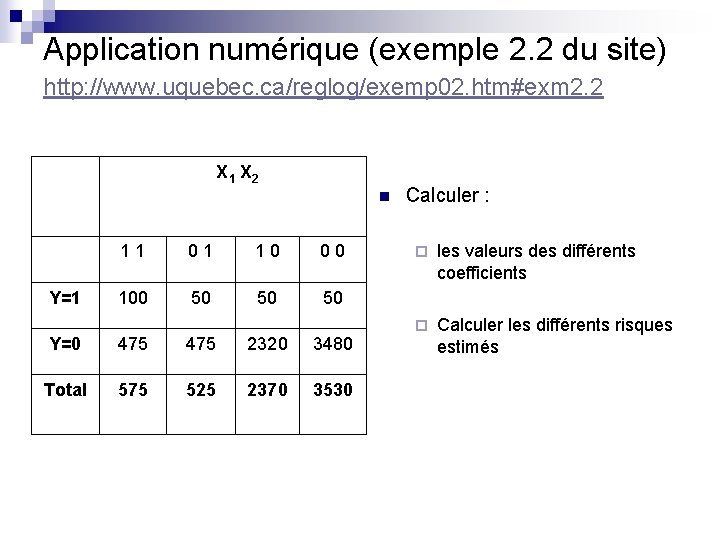
Application numérique (exemple 2. 2 du site) http: //www. uquebec. ca/reglog/exemp 02. htm#exm 2. 2 X 1 X 2 n Y=1 11 01 10 00 100 50 50 50 Y=0 475 2320 3480 Total 575 525 2370 3530 Calculer : ¨ les valeurs des différents coefficients ¨ Calculer les différents risques estimés

Deux variables indépendantes dichotomiques n Avec « 00 » comme référence X 1 X 2 11 01 10 00 Y=1 100 50 50 50 Y=0 475 2320 3480 Total 575 525 2370 3530 n L’équation s’écrit alors g(X 1, X 2)= -4, 2428+ 0, 4055*X 1 + 1, 9915*X 2 + 0, 2877*X 1*X 2

Deux variables indépendantes dichotomiques n Avec « 00 » comme référence g(X 1, X 2)= -4, 2428+ 0, 4055*X 1 + 1, 9915*X 2 + 0, 2877 X 1*X 2)

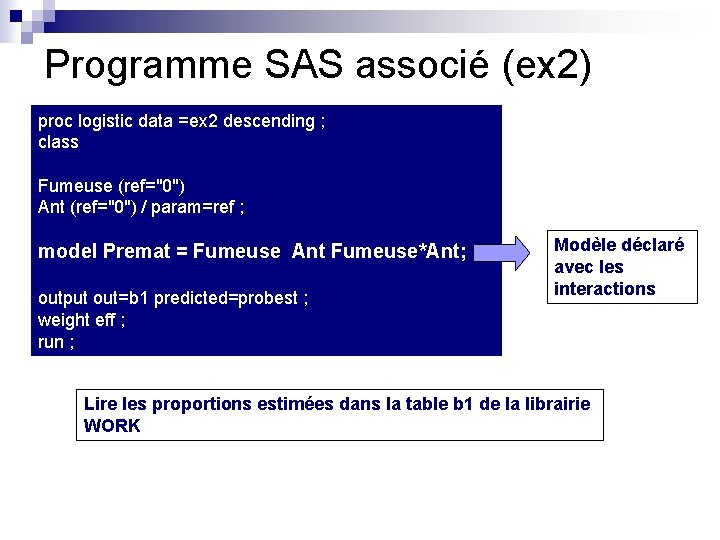
Programme SAS associé (ex 2) proc logistic data =ex 2 descending ; class Fumeuse (ref="0") Ant (ref="0") / param=ref ; model Premat = Fumeuse Ant Fumeuse*Ant; output out=b 1 predicted=probest ; weight eff ; run ; Modèle déclaré avec les interactions Lire les proportions estimées dans la table b 1 de la librairie WORK

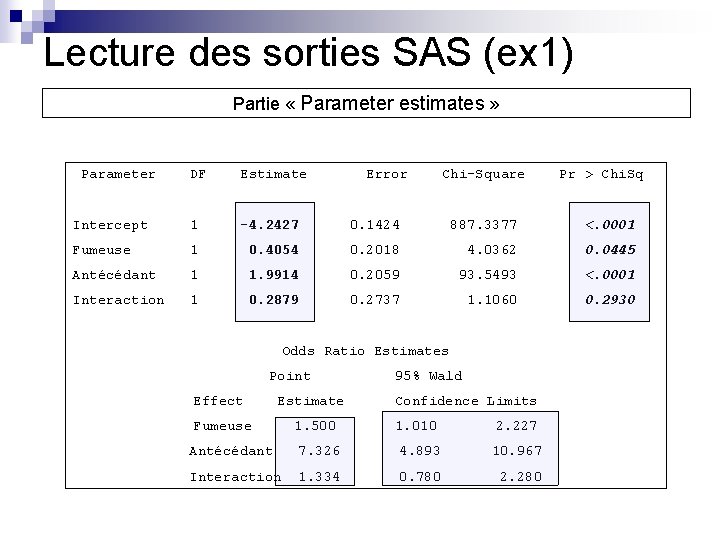
Lecture des sorties SAS (ex 1) Partie « Parameter estimates » Parameter DF Estimate Error Chi-Square Intercept 1 -4. 2427 0. 1424 887. 3377 <. 0001 Fumeuse 1 0. 4054 0. 2018 4. 0362 0. 0445 Antécédant 1 1. 9914 0. 2059 93. 5493 <. 0001 Interaction 1 0. 2879 0. 2737 1. 1060 0. 2930 Odds Ratio Estimates Point Effect Estimate Fumeuse 95% Wald Confidence Limits 1. 500 1. 010 2. 227 Antécédant 7. 326 4. 893 10. 967 Interaction 1. 334 0. 780 2. 280 Pr > Chi. Sq

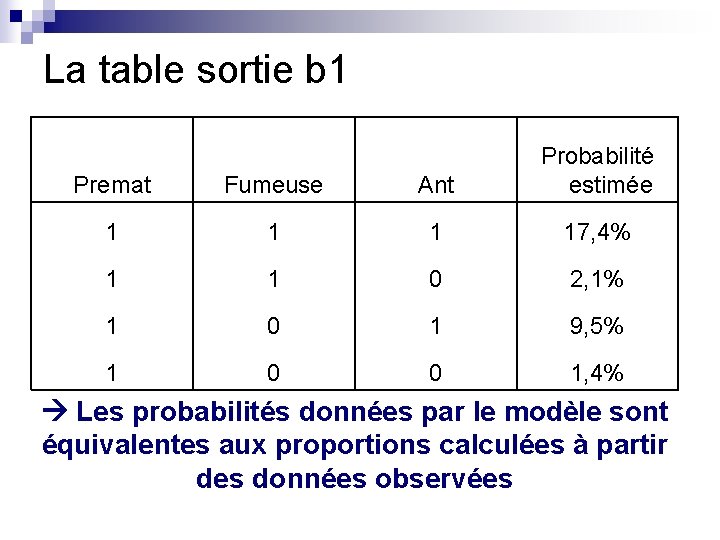
La table sortie b 1 Premat Fumeuse Ant Probabilité estimée 1 17, 4% 1 1 0 2, 1% 1 0 1 9, 5% 1 0 0 1, 4% Les probabilités données par le modèle sont équivalentes aux proportions calculées à partir des données observées

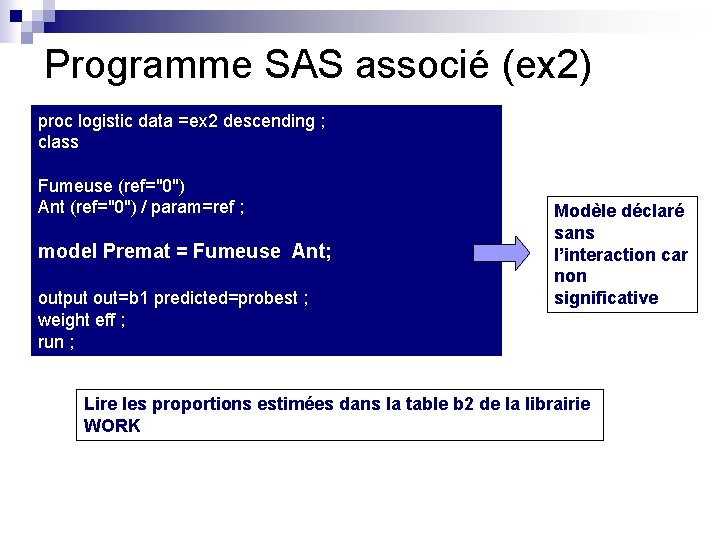
Programme SAS associé (ex 2) proc logistic data =ex 2 descending ; class Fumeuse (ref="0") Ant (ref="0") / param=ref ; model Premat = Fumeuse Ant; output out=b 1 predicted=probest ; weight eff ; run ; Modèle déclaré sans l’interaction car non significative Lire les proportions estimées dans la table b 2 de la librairie WORK

Lecture des sorties SAS (ex 2) Partie « Parameter estimates » Analysis of Maximum Likelihood Estimates Parameter Intercept Fumeuse Ant Standard Estimate DF 1 1 1 -4. 3243 0. 5631 2. 1556 Wald Error Chi-Square 0. 1243 0. 1354 0. 1346 Pr > Chi. Sq 1209. 8527 17. 2963 256. 5120 Odds Ratio Estimates Effect Fumeuse 1 vs 0 Ant 1 vs 0 Point Estimate 1. 756 8. 633 95% Wald Confidence 1. 347 6. 631 Limits 2. 290 11. 239 <. 0001

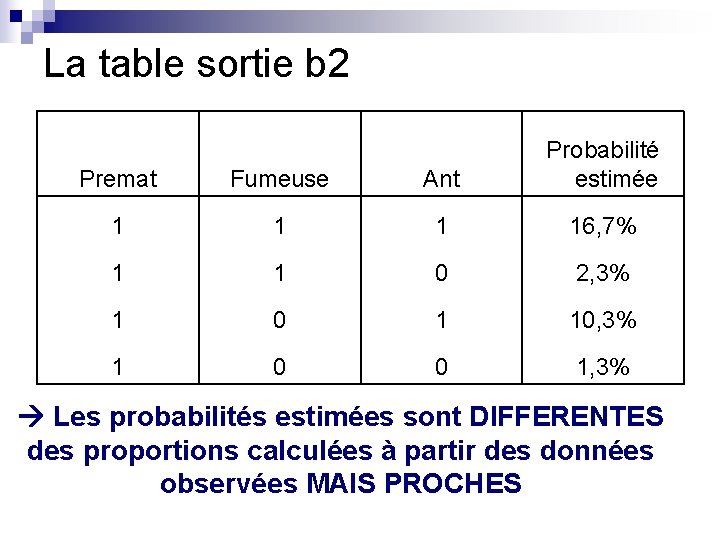
La table sortie b 2 Premat Fumeuse Ant Probabilité estimée 1 16, 7% 1 1 0 2, 3% 1 0 1 10, 3% 1 0 0 1, 3% Les probabilités estimées sont DIFFERENTES des proportions calculées à partir des données observées MAIS PROCHES

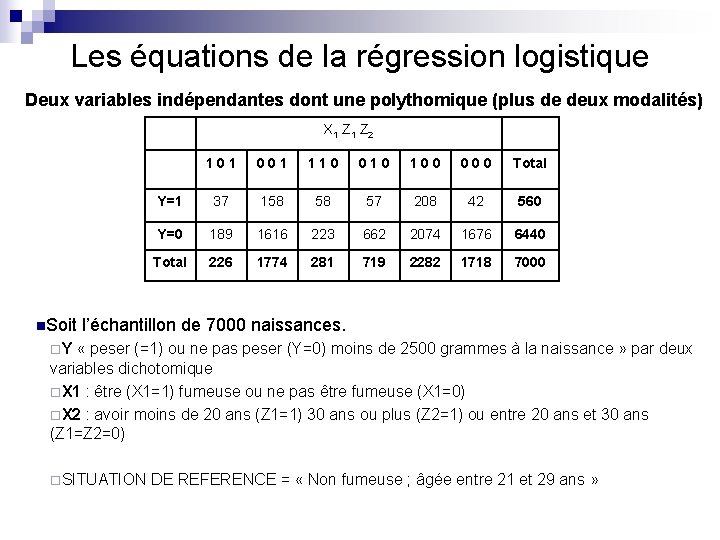
Les équations de la régression logistique Deux variables indépendantes dont une polythomique (plus de deux modalités) X 1 Z 2 n. Soit 101 001 110 010 100 000 Total Y=1 37 158 58 57 208 42 560 Y=0 189 1616 223 662 2074 1676 6440 Total 226 1774 281 719 2282 1718 7000 l’échantillon de 7000 naissances. ¨Y « peser (=1) ou ne pas peser (Y=0) moins de 2500 grammes à la naissance » par deux variables dichotomique ¨X 1 : être (X 1=1) fumeuse ou ne pas être fumeuse (X 1=0) ¨X 2 : avoir moins de 20 ans (Z 1=1) 30 ans ou plus (Z 2=1) ou entre 20 ans et 30 ans (Z 1=Z 2=0) ¨SITUATION DE REFERENCE = « Non fumeuse ; âgée entre 21 et 29 ans »

Programme SAS associé (ex 3) proc logistic data =ex 3 descending ; class Fumeuse (ref="0") Age 20 m (ref="0") Age 30 p (ref="0") / param=ref ; model Premat = Fumeuse Age 20 m Age 30 p Fumeuse*Age 20 m Fumeuse*Age 30 p Age 20 m*Age 30 p ; output out=b 3 predicted=probest ; weight eff ; run ;

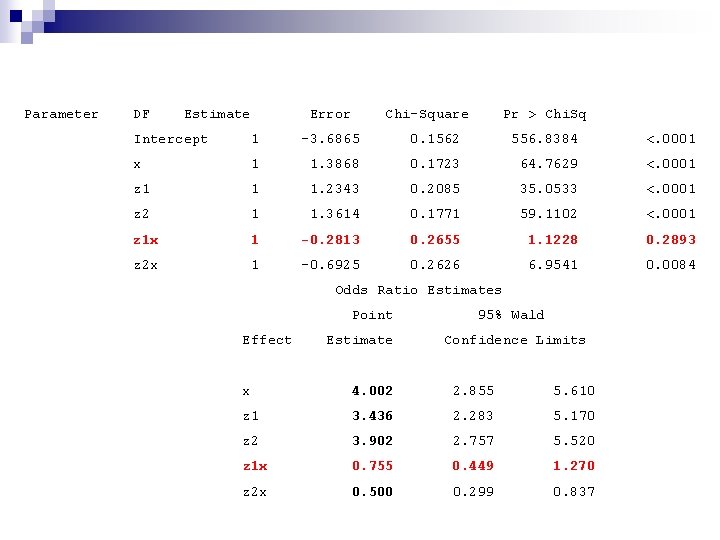
Parameter DF Estimate Error Chi-Square Pr > Chi. Sq Intercept 1 -3. 6865 0. 1562 556. 8384 <. 0001 x 1 1. 3868 0. 1723 64. 7629 <. 0001 z 1 1 1. 2343 0. 2085 35. 0533 <. 0001 z 2 1 1. 3614 0. 1771 59. 1102 <. 0001 z 1 x 1 -0. 2813 0. 2655 1. 1228 0. 2893 z 2 x 1 -0. 6925 0. 2626 6. 9541 0. 0084 Odds Ratio Estimates Point Effect Estimate 95% Wald Confidence Limits x 4. 002 2. 855 5. 610 z 1 3. 436 2. 283 5. 170 z 2 3. 902 2. 757 5. 520 z 1 x 0. 755 0. 449 1. 270 z 2 x 0. 500 0. 299 0. 837

Lecture des sorties SAS (ex 3) Parameter DF Intercept Fumeuse 1 Age 20 m 1 Age 30 p 1 Fumeuse*Age 20 m 1 1 Fumeuse*Age 30 p 1 1 n Estimate 1 1 1 -3. 6865 1. 3868 1. 2343 1. 3614 -0. 2813 -0. 6925 Pr > Chi. Sq <. 0001 0. 2893 0. 0084 L’équation s’écrit g(X 1 ; Z 1, Z 2) = -3, 68 + 1, 38 X 1 + 1, 23 Z 1 + 1, 36 Z 2 - 0, 28 X 1*Z 1 -0, 69 X 1*Z 2

OR = e 1, 3868 Effect Point Estimate Fumeuse Age 20 m Age 30 p Fumeuse*Age 20 m Fumeuse*Age 30 p 4. 002 3. 436 3. 902 0. 755 0. 500 Confidence Limits 2. 855 2. 283 2. 757 0. 449 0. 299 5. 610 5. 170 5. 520 1. 270 0. 837 e -0, 2823 = 0, 755 = 3, 02/4, 002 l’effet modifiant de l'âge de la mère sur l’association entre " le fait de fumer " et " le faible poids à la naissance Cet effet d’interaction est marqué par le coefficient négatif de Z 1 : -0, 2813 Le rapport entre les enfants de moins de 2500 et ceux de plus de 2500 g est 4 fois plus important chez les fumeuses âgées de 2030 ans que chez les non fumeuses du même groupe d’âges. mesure l’association entre " le fait de -faible poids à la naissance (Y) -fumer pendant la grossesse (X 1) -âge "20<=age<30 ans « (Z) -OR n’est pas significatif. Ic compris de chacun des côté de 1 Pour mesurer l’association entre -le " faible poids à la naissance (Y=1) « Fumeuse * Age 30 p = effet négatif = avoir 30 ans diminue le risque d’avoir un enfant prématuré quand on est fumeuse. - le fait de fumer pendant la grossesse (X 1=1 ) L’effet est significatif !!! Vaut : e (1, 3868*1 -0, 2813*1)=3, 02 = OR -l'âge de la mère est "<20 ans" :

Programme SAS sans les associations entre les variables proc logistic data =ex 3 descending ; class Fumeuse (ref="0") Age 20 m (ref="0") Age 30 p (ref="0") / param=ref ; model Premat = Fumeuse Age 20 m Age 30 p ; output out=b 3 predicted=probest ; weight eff ; run ;

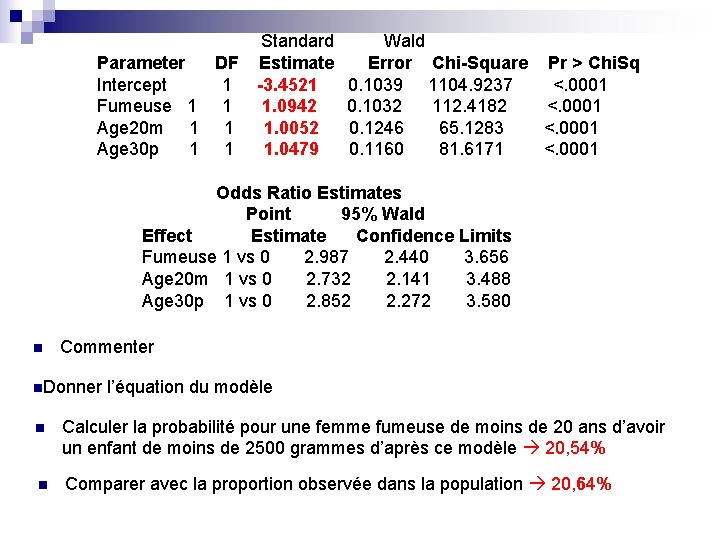
Parameter DF Intercept 1 Fumeuse 1 1 Age 20 m 1 1 Age 30 p 1 1 Standard Estimate -3. 4521 1. 0942 1. 0052 1. 0479 Wald Error Chi-Square Pr > Chi. Sq 0. 1039 1104. 9237 <. 0001 0. 1032 112. 4182 <. 0001 0. 1246 65. 1283 <. 0001 0. 1160 81. 6171 <. 0001 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits Fumeuse 1 vs 0 2. 987 2. 440 3. 656 Age 20 m 1 vs 0 2. 732 2. 141 3. 488 Age 30 p 1 vs 0 2. 852 2. 272 3. 580 n Commenter n. Donner l’équation du modèle n Calculer la probabilité pour une femme fumeuse de moins de 20 ans d’avoir un enfant de moins de 2500 grammes d’après ce modèle 20, 54% n Comparer avec la proportion observée dans la population 20, 64%