Les IDENTITS TRIGONOMTRIQUES y Radian et longueur darc














- Slides: 31

Les IDENTITÉS TRIGONOMÉTRIQUES

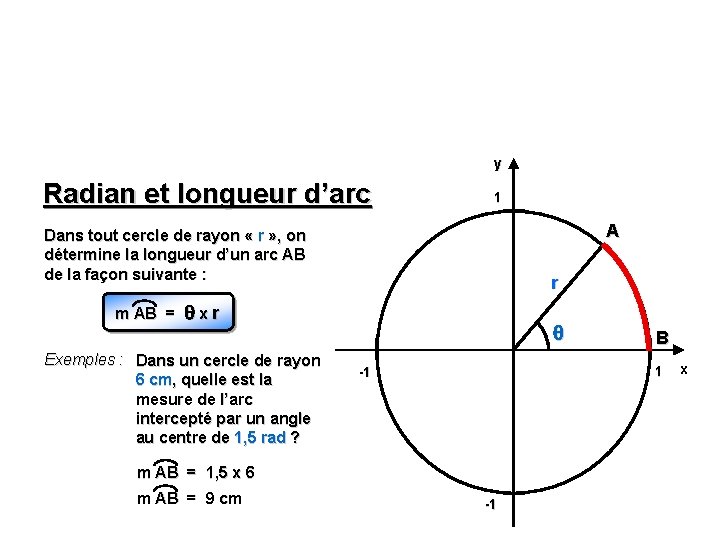
y Radian et longueur d’arc 1 A Dans tout cercle de rayon « r » , on détermine la longueur d’un arc AB de la façon suivante : m AB = r xr Exemples : Dans un cercle de rayon 6 cm, quelle est la mesure de l’arc intercepté par un angle au centre de 1, 5 rad ? 1 -1 m AB = 1, 5 x 6 m AB = 9 cm B -1 x

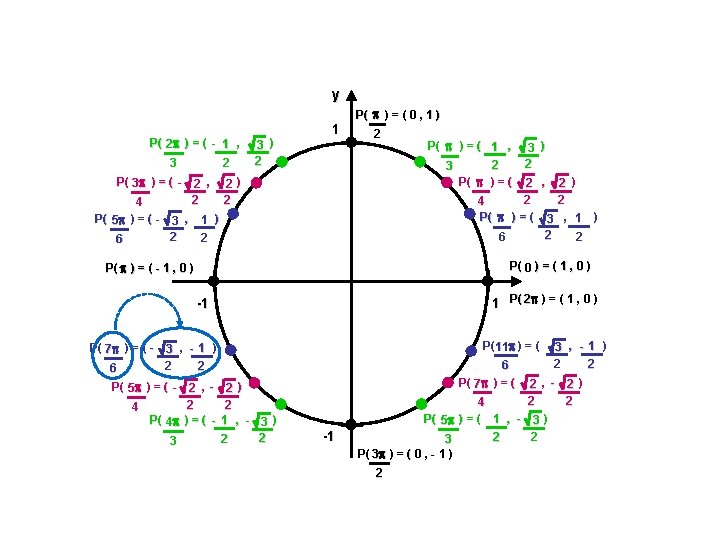
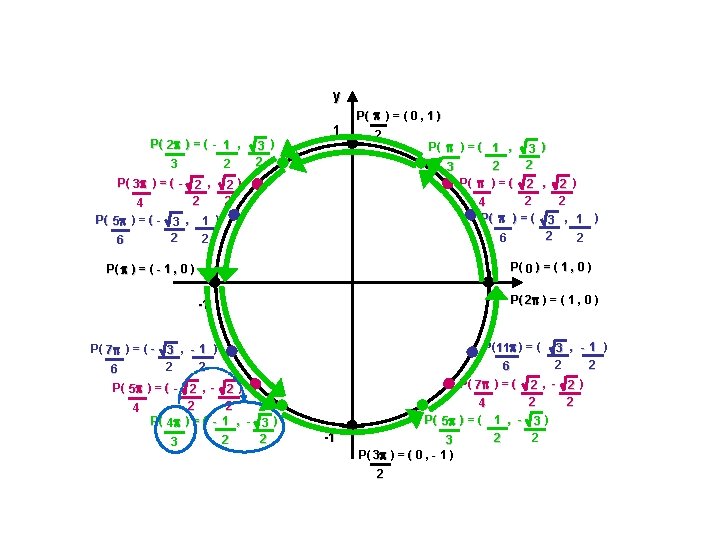
Coordonnées équivalentes du cercle trigonométrique Ex. : Déterminer les coordonnées du point correspondant sur le cercle trigonométrique. Exprimer la valeur exacte lorsque c’est possible. a) 7 6 rad


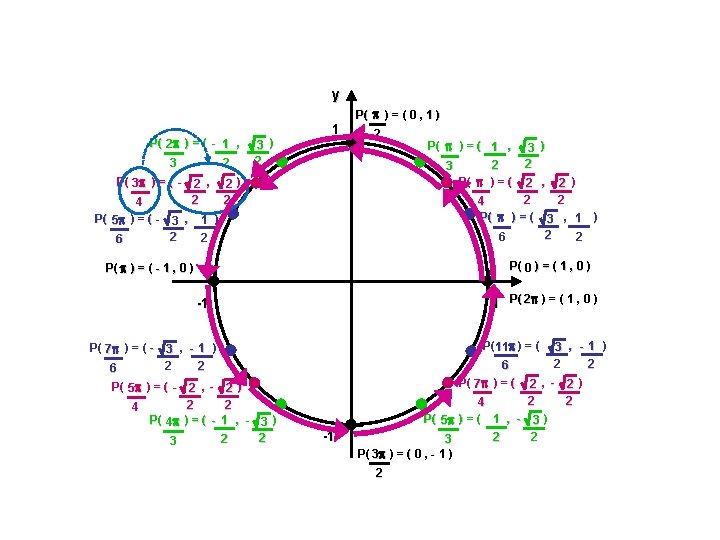
Coordonnées équivalentes du cercle trigonométrique Ex. : Déterminer les coordonnées du point correspondant sur le cercle trigonométrique. Exprimer la valeur exacte lorsque c’est possible. a) b) 7 6 - 4 rad Réponse : ( - 3 2 rad , -1 ) 2


Coordonnées équivalentes du cercle trigonométrique Ex. : Déterminer les coordonnées du point correspondant sur le cercle trigonométrique. Exprimer la valeur exacte lorsque c’est possible. a) b) c) 7 6 - 4 11 4 rad Réponse : ( - 3 -1 ) , 2 2 rad Réponse : ( 2 , - 2 ) 2 rad 2


Coordonnées équivalentes du cercle trigonométrique Ex. : Déterminer les coordonnées du point correspondant sur le cercle trigonométrique. Exprimer la valeur exacte lorsque c’est possible. a) b) c) d) 7 6 - 4 11 4 10 3 rad Réponse : ( - 3 -1 ) , 2 2 rad Réponse : ( 2 , - 2 ) 2 rad Réponse : ( - 2 2 rad 2 , 2 ) 2


Coordonnées équivalentes du cercle trigonométrique Ex. : Déterminer les coordonnées du point correspondant sur le cercle trigonométrique. Exprimer la valeur exacte lorsque c’est possible. a) b) c) d) 7 6 - 4 11 4 10 3 rad Réponse : ( - 3 -1 ) , 2 2 rad Réponse : ( 2 , - 2 ) 2 rad Réponse : ( - 2 2 , 2 ) 2 2 Réponse : ( -1 , - 3 2 2 )

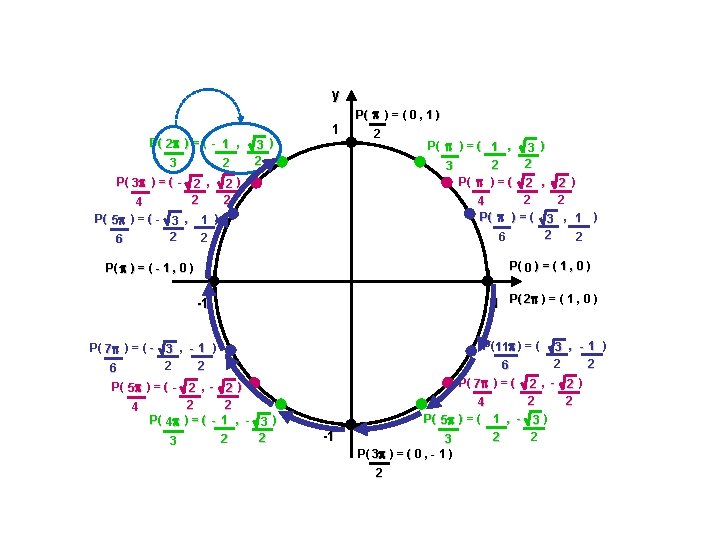
Coordonnées équivalentes du cercle trigonométrique Ex. : Déterminer les coordonnées du point correspondant sur le cercle trigonométrique. Exprimer la valeur exacte lorsque c’est possible. e) - 8 6 rad


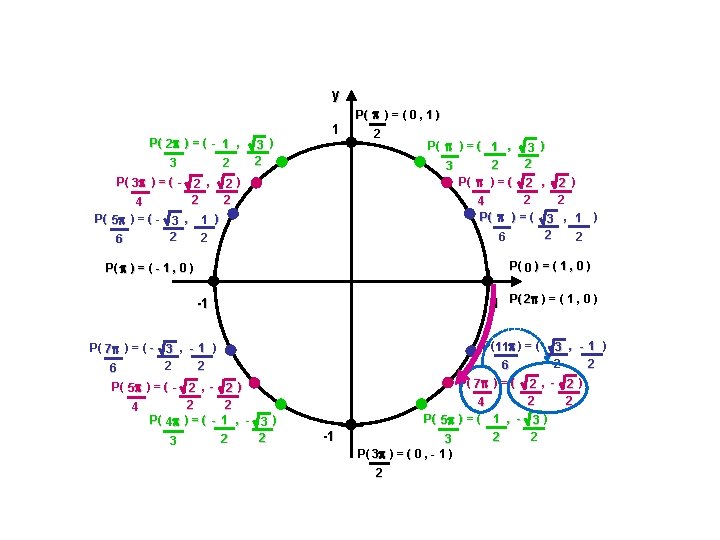
Coordonnées équivalentes du cercle trigonométrique Ex. : Déterminer les coordonnées du point correspondant sur le cercle trigonométrique. Exprimer la valeur exacte lorsque c’est possible. e) f) - 8 6 - 2 rad Réponse : ( -1 , 2 rad 3 2 )


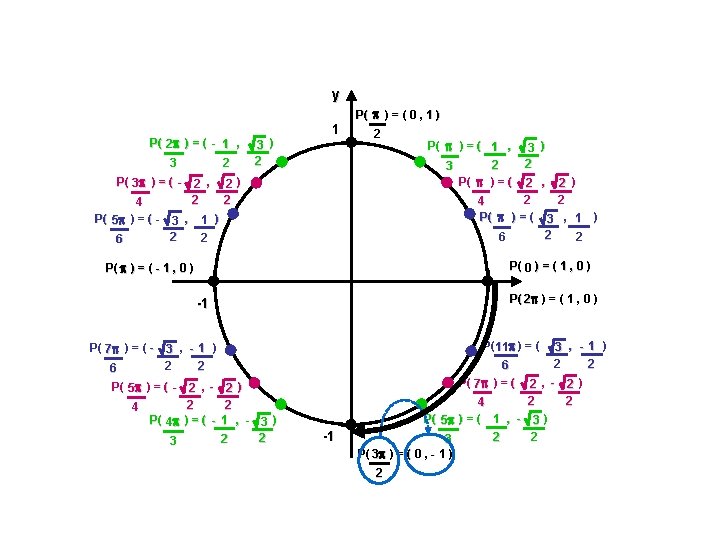
Coordonnées équivalentes du cercle trigonométrique Ex. : Déterminer les coordonnées du point correspondant sur le cercle trigonométrique. Exprimer la valeur exacte lorsque c’est possible. e) f) - 8 6 - 2 rad Réponse : ( -1 , 2 rad g) - 5 rad Réponse : ( 3 2 0 , -1 ) )


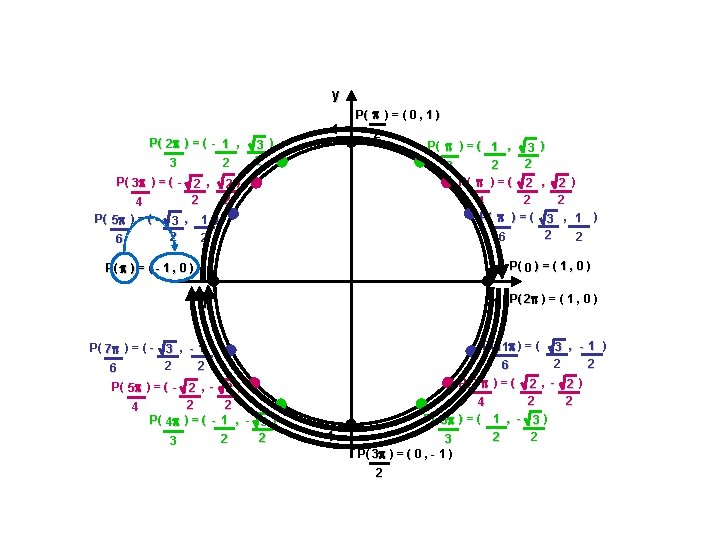
Coordonnées équivalentes du cercle trigonométrique Ex. : Déterminer les coordonnées du point correspondant sur le cercle trigonométrique. Exprimer la valeur exacte lorsque c’est possible. e) f) - 8 6 - 2 rad g) - 5 rad h) 11 8 Réponse : ( -1 , rad Réponse : ( 3 ) 2 0 , -1 ) Réponse : ( - 1 , 0 ) Réponse : ( cos 11 , sin 11 8 8 ( - 0, 3827 , - 0, 9239 ) )

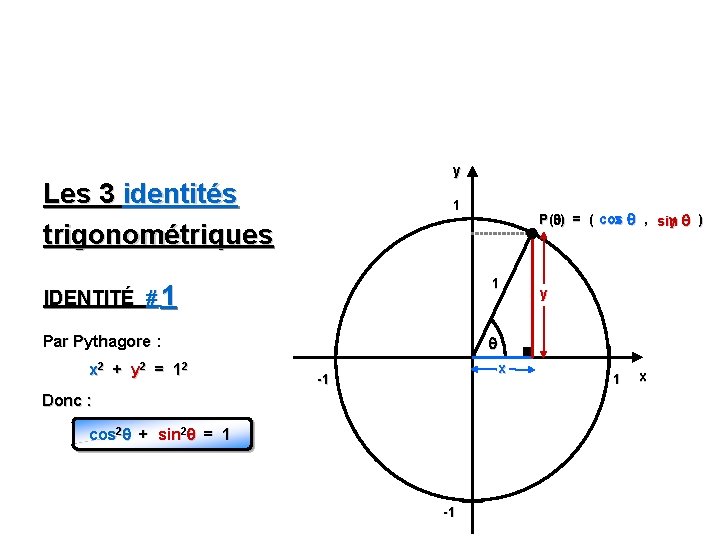
y Les 3 identités trigonométriques 1 P( ) = ( cos x , sin y ) IDENTITÉ # 1 1 Par Pythagore : x 2 + y 2 = 1 2 x -1 Donc : cos 2 + sin 2 = 1 -1 y 1 x

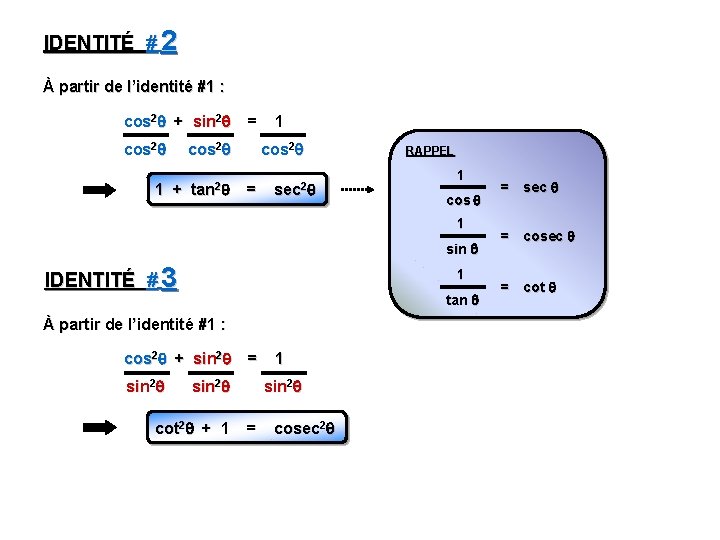
IDENTITÉ # 2 À partir de l’identité #1 : cos 2 + sin 2 cos 2 1 + = cos 2 tan 2 1 cos 2 = sec 2 RAPPEL 1 cos 1 sin IDENTITÉ # 3 1 tan À partir de l’identité #1 : cos 2 + sin 2 = sin 2 cot 2 + 1 1 sin 2 = cosec 2 = sec = cot

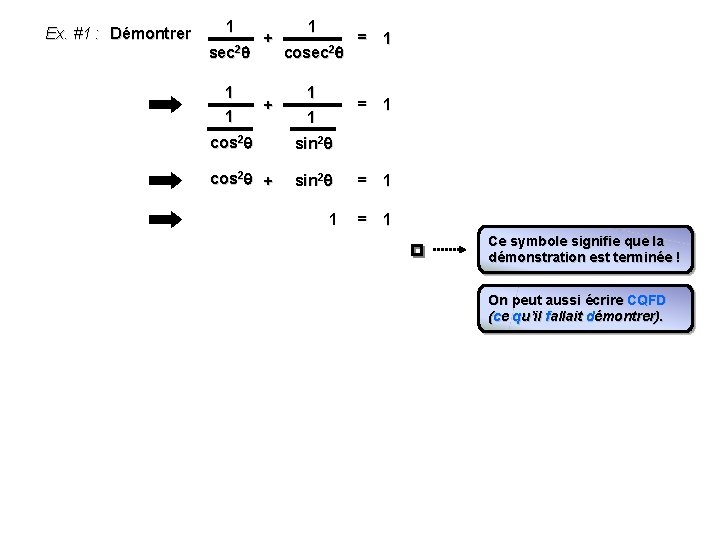
Ex. #1 : Démontrer 1 sec 2 1 1 + + 1 cosec 2 1 1 = 1 cos 2 sin 2 cos 2 + sin 2 1 = 1 Ce symbole signifie que la démonstration est terminée ! On peut aussi écrire CQFD (ce qu’il fallait démontrer).

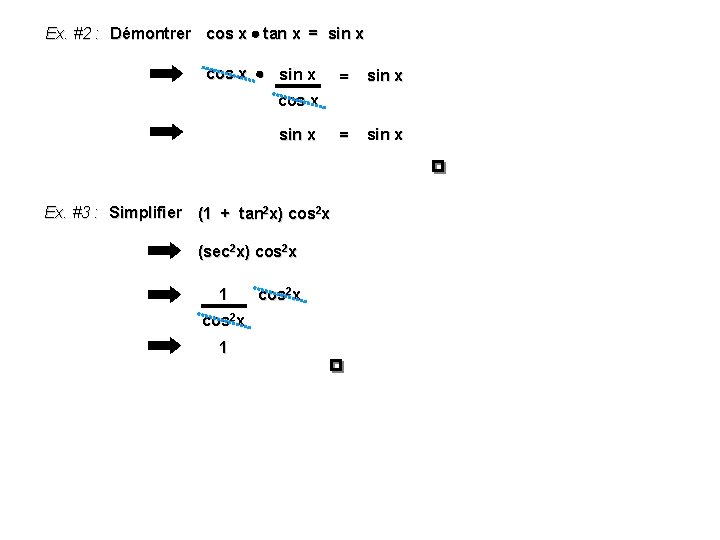
Ex. #2 : Démontrer cos x tan x = sin x cos x sin x = sin x cos x sin x Ex. #3 : Simplifier (1 + tan 2 x) cos 2 x (sec 2 x) cos 2 x 1 cos 2 x

Ex. #4 : Démontrer tan 2 x – tan 2 x sin 2 x = sin 2 x tan 2 x (1 – sin 2 x) = sin 2 x tan 2 x (cos 2 x) = sin 2 x sin 2 x (cos 2 x) = sin 2 x cos 2 x sin 2 x = sin 2 x

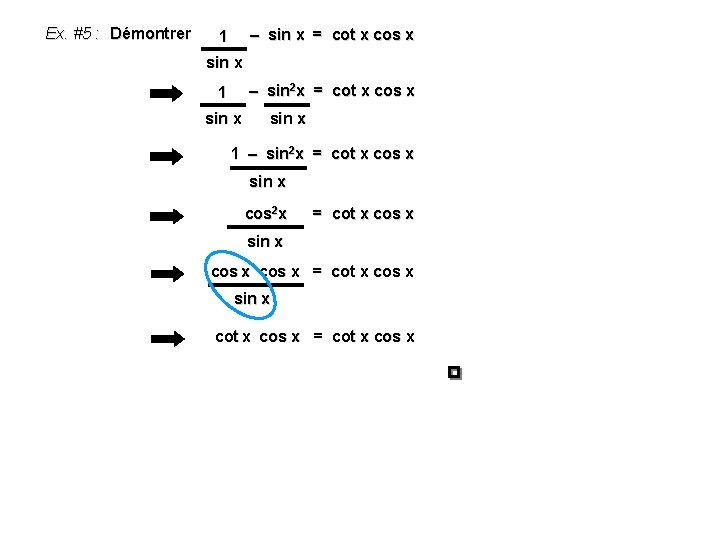
Ex. #5 : Démontrer – sin x = cot x cos x 1 sin x – sin 2 x = cot x cos x 1 sin x 1 – sin 2 x = cot x cos x sin x cos x = cot x cos x sin x cot x cos x = cot x cos x

Autres identités Somme de u et v sin (u + v) = sin(u) cos(v) + sin(v) cos(u) cos (u + v) = cos(u) cos(v) – sin(u) sin(v) Ex. : Soit u = et v = , calculer précisément sin ( 4 3 + 4 3 ).

Somme de u et v sin (u + v) = sin(u) cos(v) + sin(v) cos(u) cos (u + v) = cos(u) cos(v) – sin(u) sin(v) Ex. : Soit u = et v = , calculer précisément sin (u + v). 3 4 sin ( + ) = sin ( ) cos ( ) 4 3 sin ( 7 ) = 12 ( 1 2 ) 2 ( 2 ) + 4 ( + ) 4 ( 3 2 6 4 2 4 3 2 6 + sin ( ) cos ( ) 3 4 ( + ) ) ( 2 2 )

Différence entre u et v sin (u – v) = sin(u) cos(v) – sin(v) cos(u) cos (u – v) = cos(u) cos(v) + sin(u) sin(v) Ex. : Soit u = 3 et v = 2 , calculer précisément cos (u – v). 3 4 cos ( 3 – 2 ) = cos ( 3 ) cos ( 2 ) 4 cos ( ) = ( -1 ) 2 2 ( + 2 ) 12 4 ) = 2 + 12 4 ( - 2 ) 12 cos ( 3 4 3 ( + 6 ) 4 4 + sin ( 3 ) sin ( 2 ) 6 ( 3 2 ) ( 3 2 2 )


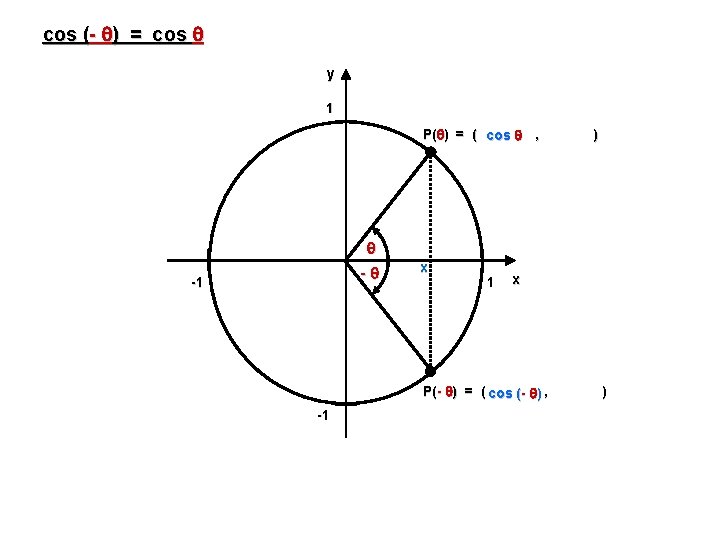
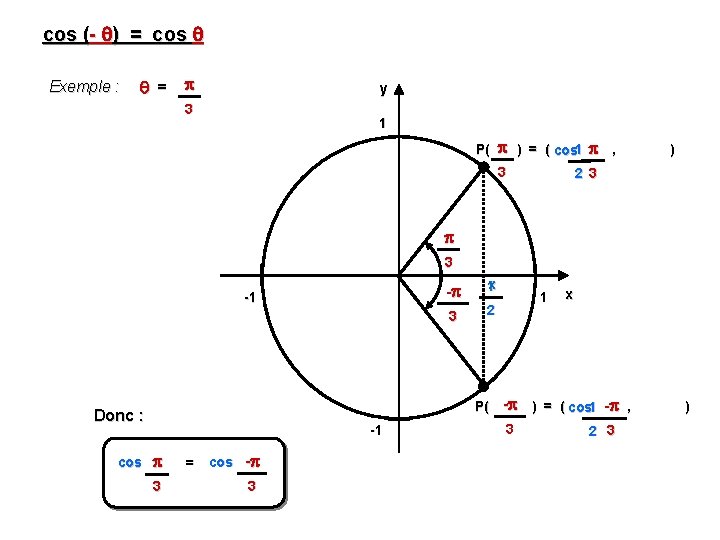
cos (- ) = cos Exemple : = y 3 1 P( ) = ( cos 1 , 3 ) 2 3 3 -1 - 1 x 3 2 1 P( - Donc : -1 cos = cos - 3 3 3 x ) = ( cos 1 - , 2 3 )


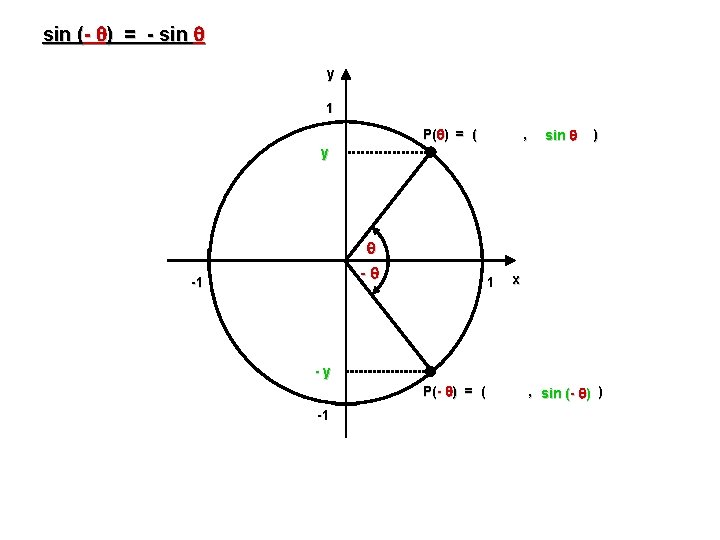
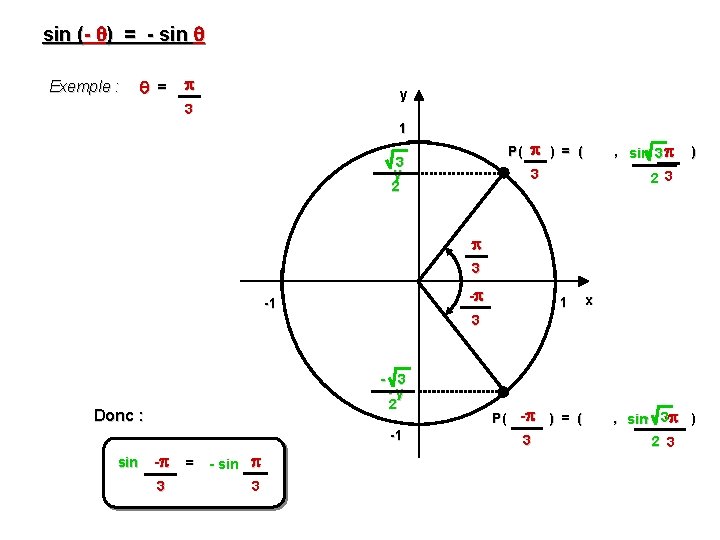
sin (- ) = - sin Exemple : = y 3 1 P( ) = ( 3 y 2 , sin 3 3 ) 2 3 3 - -1 1 x 3 -y 2 Donc : -1 sin - = - sin 3 3 P( - 3 ) = ( , sin- 3 - ) 2 3