Les Graphes Graphes Un graphe G V E

Les Graphes

Graphes Un graphe G = (V, E) consiste en un ensemble V de noeud, et un ensemble E d’arêtes, tels que chaque arête dans E relie une paire de nœuds dans V. Le nombre de nœuds est dénoté |V|, et le nombre d’arêtes est dénoté |E|.

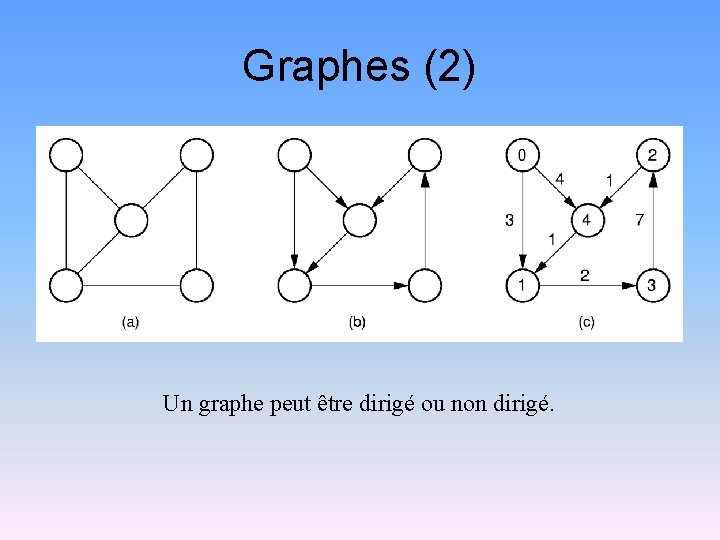
Graphes (2) Un graphe peut être dirigé ou non dirigé.

Chemins et cycles Chemin (de longueur n): Une séquence de noeuds v 0, v 1, …, vn avec une arête de vi à vi+1 pour chaque 0 <= i < n. Un chemin est simple si tous les nœuds dans le chemin sont distincts. Un cycle est un chemin de longueur 3 ou plus reliant un nœud vi à lui même. Un cycle est simple si le chemin est simple, sauf que les premiers et derniers nœuds sont les même.

Composantes connexes Un graphe non dirigé est connexe s’il existe un chemin entre toutes les paires de nœuds. Les sous-graphes connexes maximaux sont appelés composantes connexes

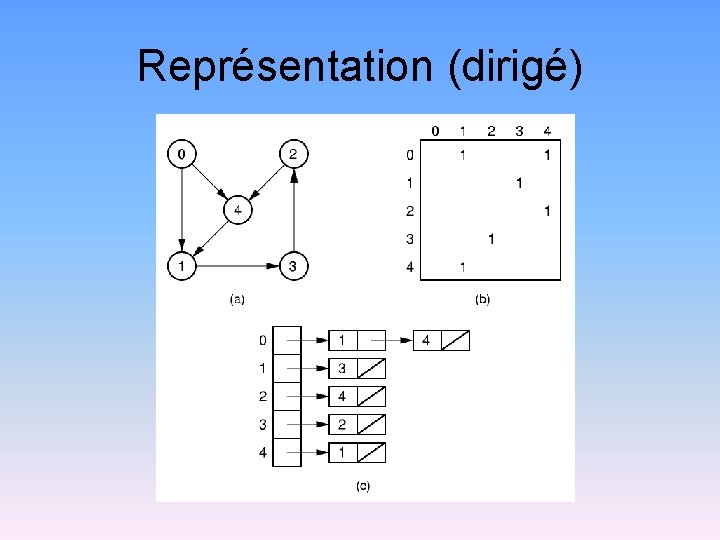
Représentation (dirigé)

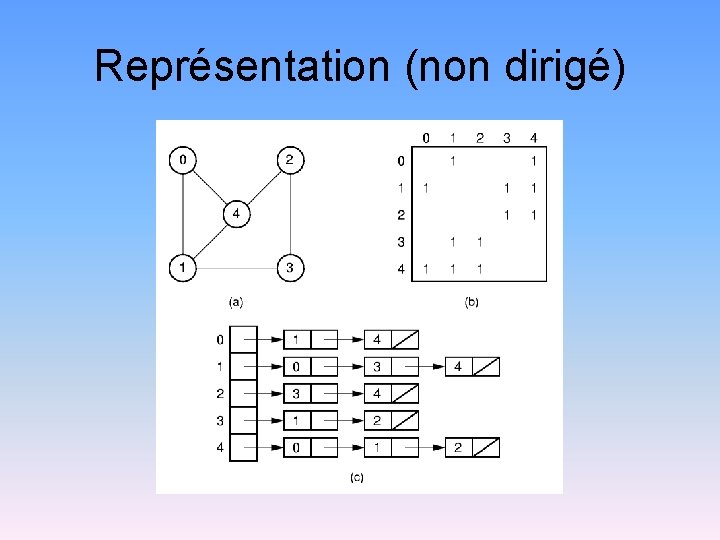
Représentation (non dirigé)

Coût de la représentation Matrice d’adjacence: Listes d’adjacence:

Graphe: Type de donnée abstrait class Graph { // Classe abstraite public: virtual int n() =0; // # de noeuds virtual int e() =0; // # d’arêtes // Retourne l’indice du premier voisin virtual int first(int) =0; // Retourne l’indice de prochain voisin virtual int next(int, int) =0; // Insère une nouvelle arête virtual void set. Edge(int, int) =0; // Enlève une arête virtual void del. Edge(int, int) =0; // Retourne la longueur de l’arête virtual int weight(int, int) =0; // Retourne la valeur d’un noeud virtual int get. Mark(int) =0; // Assigne une valeur à un noeud virtual void set. Mark(int, int) =0; };

Implémentation (matrice d’adjacence) #define UNVISITED 0 #define VISITED 1 class Graphm : public Graph { private: int num. Vertex, num. Edge; int **matrix; int *mark; public:

Graphm(int num. Vert) { int i, j; num. Vertex = num. Vert; num. Edge = 0; mark = new int[num. Vert]; for (i=0; i<num. Vertex; i++) mark[i] = UNVISITED; matrix = (int**) new int*[num. Vertex]; for (i=0; i<num. Vertex; i++) matrix[i] = new int[num. Vertex]; for (i=0; i< num. Vertex; i++) for (int j=0; j<num. Vertex; j++) matrix[i][j] = 0; }

~Graphm() { delete [] mark; for (int i=0; i<num. Vertex; i++) delete [] matrix[i]; delete [] matrix; } int n() { return num. Vertex; } int e() { return num. Edge; }

int first(int v) { int i; for (i=0; i<num. Vertex; i++) if (matrix[v][i] != 0) return i; } // Donne le voisin de v 1 après v 2 int next(int v 1, int v 2) { int i; for(i=v 2+1; i<num. Vertex; i++) if (matrix[v 1][i] != 0) return i; }

void set. Edge(int v 1, int v 2, int wgt) { if (matrix[v 1][v 2] == 0) num. Edge++; matrix[v 1][v 2] = wgt; } void del. Edge(int v 1, int v 2) { if (matrix[v 1][v 2] != 0) num. Edge--; matrix[v 1][v 2] = 0; } int weight(int v 1, int v 2) { return matrix[v 1][v 2]; } int get. Mark(int v) { return mark[v]; } void set. Mark(int v, int val) { mark[v] = val; } };

Implémentation (liste d’adjacence) class Edge { public: int vertex, weight; Edge() { vertex = -1; weight = -1; } Edge(int v, int w) { vertex = v; weight = w; } };

class Graphl : public Graph { private: int num. Vertex, num. Edge; List<Edge>** vertex; int *mark; public: Graphl(int num. Vert) { int i, j; num. Vertex = num. Vert; num. Edge = 0; mark = new int[num. Vert]; for (i=0; i<num. Vertex; i++) mark[i] = UNVISITED; // Crée et initialise la liste d’adjacence vertex = (List<Edge>**) new List<Edge>*[num. Vertex]; for (i=0; i<num. Vertex; i++) vertex[i] = new LList<Edge>(); }

~Graphl() { delete [] mark; for (int i=0; i<num. Vertex; i++) delete [] vertex[i]; delete [] vertex; } int n() { return num. Vertex; } int e() { return num. Edge; } int first(int v) { Edge it; vertex[v]->set. Start(); if (vertex[v]->get. Value(it)) return it. vertex; else return num. Vertex; }

int next(int v 1, int v 2) { Edge it; vertex[v 1]->get. Value(it); if (it. vertex == v 2) vertex[v 1]->next(); else { vertex[v 1]->set. Start(); while (vertex[v 1]->get. Value(it) && (it. vertex <= v 2)) vertex[v 1]->next(); } if (vertex[v 1]->get. Value(it)) return it. vertex; else return num. Vertex; }

void set. Edge(int v 1, int v 2, int wgt) { Edge it(v 2, wgt); Edge curr; vertex[v 1]->get. Value(curr); if (curr. vertex != v 2) for (vertex[v 1]->set. Start(); vertex[v 1]->get. Value(curr); vertex[v 1]->next()) if (curr. vertex >= v 2) break; if (curr. vertex == v 2) vertex[v 1]->remove(curr); else num. Edge++; vertex[v 1]->insert(it); }

void del. Edge(int v 1, int v 2) { Edge curr; vertex[v 1]->get. Value(curr); if (curr. vertex != v 2) for (vertex[v 1]->set. Start(); vertex[v 1]->get. Value(curr); vertex[v 1]->next()) if (curr. vertex >= v 2) break; if (curr. vertex == v 2) { vertex[v 1]->remove(curr); num. Edge--; } }

int weight(int v 1, int v 2) { Edge curr; vertex[v 1]->get. Value(curr); if (curr. vertex != v 2) for (vertex[v 1]->set. Start(); vertex[v 1]->get. Value(curr); vertex[v 1]->next()) if (curr. vertex >= v 2) break; if (curr. vertex == v 2) return curr. weight; else return 0; } int get. Mark(int v) { return mark[v]; } void set. Mark(int v, int val) { mark[v] = val; } };

Parcours d’un graphe Certaines applications nécessitent de visiter chaque nœuds exactement une fois. Une application peut demander de visiter les nœuds dans un ordre particulier en accord avec la topologie du graphe. Exemples: • Jeu d’échec • Chemin le plus court

Parcours d’un graphe(2) Pour s’assurer de visiter tous les noeuds: void graph. Traverse(const Graph* G) { for (v=0; v<G->n(); v++) G->set. Mark(v, UNVISITED); //Initialisation for (v=0; v<G->n(); v++) if (G->get. Mark(v) == UNVISITED) do. Traverse(G, v); }

Parcours en profondeur (1) void DFS(Graph* G, int v) { Pre. Visit(G, v); G->set. Mark(v, VISITED); for (int w=G->first(v); w<G->n(); w = G->next(v, w)) if (G->get. Mark(w) == UNVISITED) DFS(G, w); Post. Visit(G, v); }

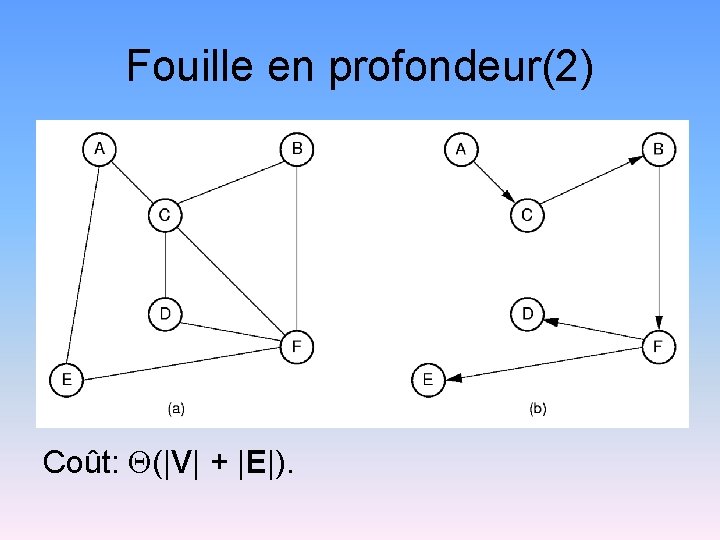
Fouille en profondeur(2) Coût: (|V| + |E|).

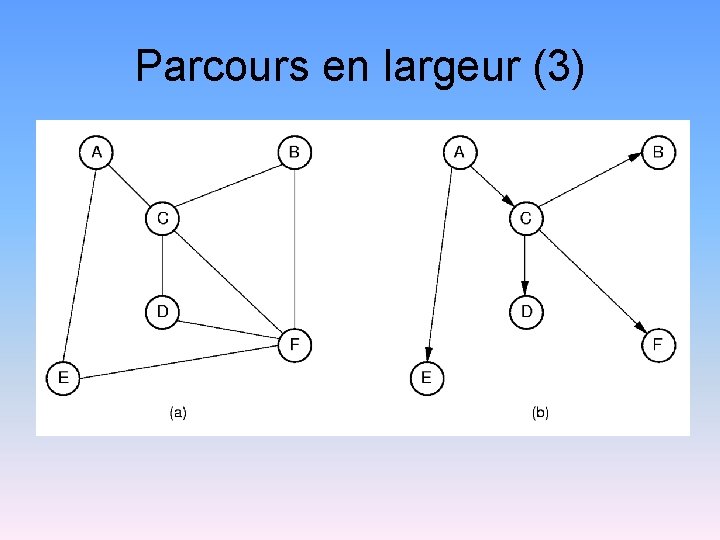
Parcours en largeur (1) Comme la fouille en profondeur, sauf qu’on remplace la pile par une file d’attente: – On visite les voisins d’un nœuds avant d’aller plus en profondeur dans le graphe.

Parcours en largeur (2) void BFS(Graph* G, int start, Queue<int>*Q) { int v, w; Q->enqueue(start); G->set. Mark(start, VISITED); while (Q->length() != 0) { Q->dequeue(v); Pre. Visit(G, v); for(w=G->first(v); w<G->n(); w=G->next(v, w)) if (G->get. Mark(w) == UNVISITED) { G->set. Mark(w, VISITED); Q->enqueue(w); } Post. Visit(G, v); } }

Parcours en largeur (3)

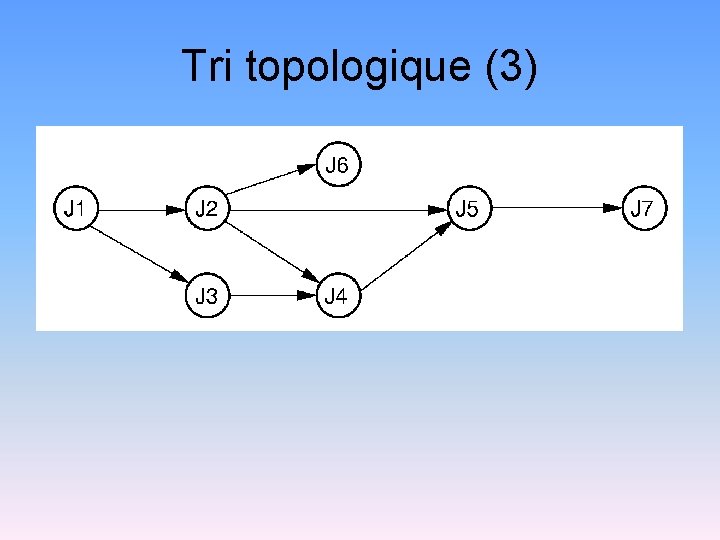
Tri topologique(1) Problème: Étant donné un ensemble de tâches à accomplir (certaines tâches devant être effectuées avant d’autres), afficher les tâches dans un ordre qui respecte leur ordonnancement.

Tri topologique(2) void topsort(Graph* G) { // Tri topologique int i; for (i=0; i<G->n(); i++) // Initialisation G->set. Mark(i, UNVISITED); for (i=0; i<G->n(); i++) // traiter chaque // composante connexe if (G->get. Mark(i) == UNVISITED) tophelp(G, i); } void tophelp(Graph* G, int v) { G->set. Mark(v, VISITED); for (int w=G->first(v); w<G->n(); w = G->next(v, w)) if (G->get. Mark(w) == UNVISITED) tophelp(G, w); printout(v); // Post. Visite }

Tri topologique (3)

Utiliser une file void topsort(Graph* G, Queue<int>* Q) { int Count[G->n()]; int v, w; for (v=0; v<G->n(); v++) Count[v] = 0; for (v=0; v<G->n(); v++) for (w=G->first(v); w<G->n(); w = G->next(v, w)) Count[w]++; // Add to v 2's count for (v=0; v<G->n(); v++) // Initialise Q if (Count[v] == 0) Q->enqueue(v); while (Q->length() != 0) { Q->dequeue(v) printout(v); // PréVisite de V for (w=G->first(v); w<G->n(); w = G->next(v, w)) { Count[w]--; if (Count[w] == 0) Q->enqueue(w); }}}