LES GRAPHES 1DEFINITION graphe simple orient DEFINITION Un









































































- Slides: 111

LES GRAPHES

1)DEFINITION graphe ( simple orienté )

DEFINITION • Un graphe ( simple orienté ) c’est un couple ( X, U ) avec X un ensemble fini et U une partie du produit cartésien X 2

Exemple : • X = • U = • Les éléments de X sont les sommets ou points du graphe • Les éléments de U sont les arcs du graphe • Un graphe est valué si à chaque arc est associé un nombre

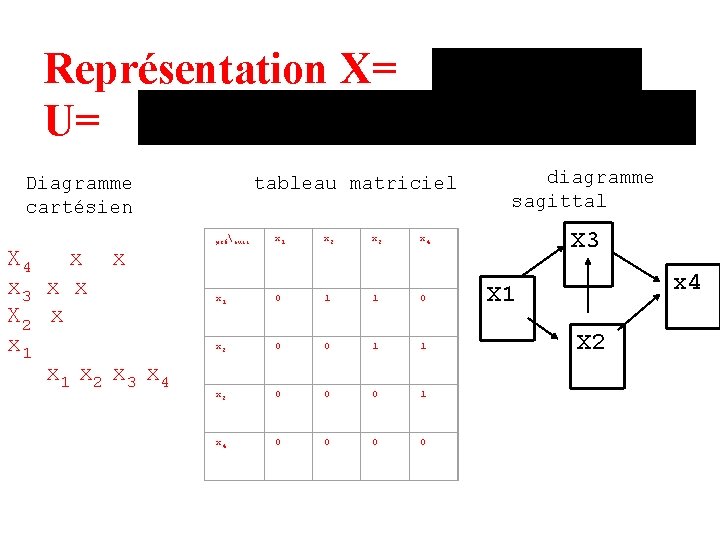
Représentation X= U= Diagramme cartésien X 4 x x x 3 x x X 2 x x 1 x 2 x 3 x 4 tableau matriciel présucc x 1 x 2 x 3 x 4 x 1 0 1 1 0 x 2 0 0 1 1 x 3 0 0 0 1 x 4 0 0 diagramme sagittal X 3 x 4 X 1 X 2

2)PLANIFICATION DE L’ORDONNANCEMENT DES TACHES :

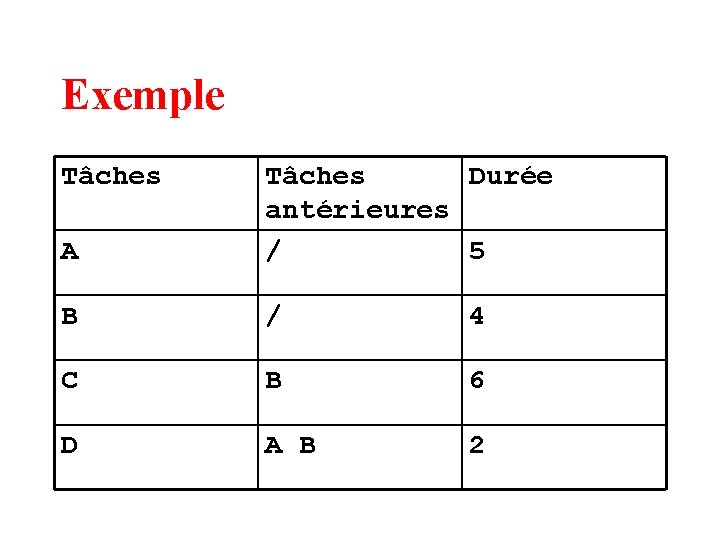
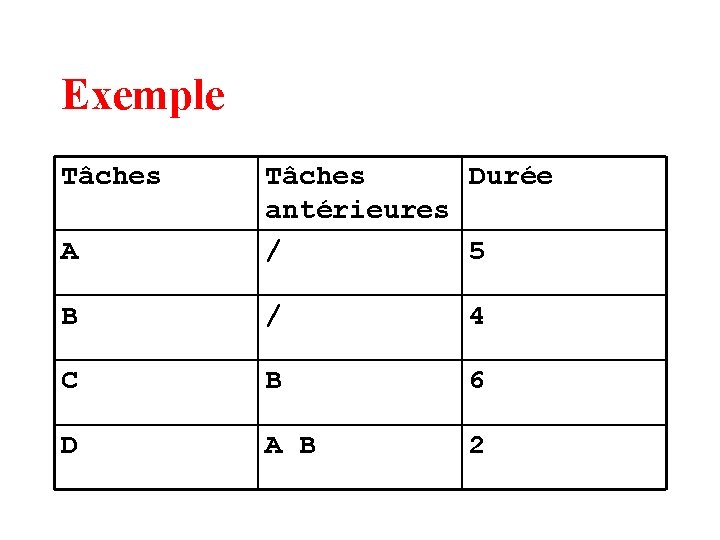
Exemple Tâches A Tâches Durée antérieures / 5 B / 4 C B 6 D A B 2

DEUX METHODES • a)La méthode P. E. R. T • b)La méthode M. P. M.

a)La méthode P. E. R. T

méthode P. E. R. T • Chaque arc représente une tâche il est valué par la durée de la tâche A 5 D 2 B 4 C 6 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2

méthode P. E. R. T • Chaque sommet représente une étape X 3 A 5 D 2 X 4 X 1 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2 C 6 B 4 X 2

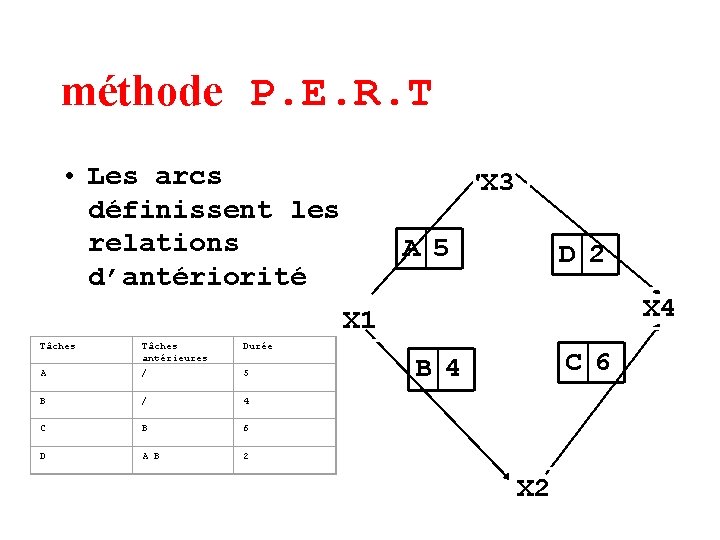
méthode P. E. R. T • Les arcs définissent les relations d’antériorité X 3 A 5 D 2 X 4 X 1 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2 C 6 B 4 X 2

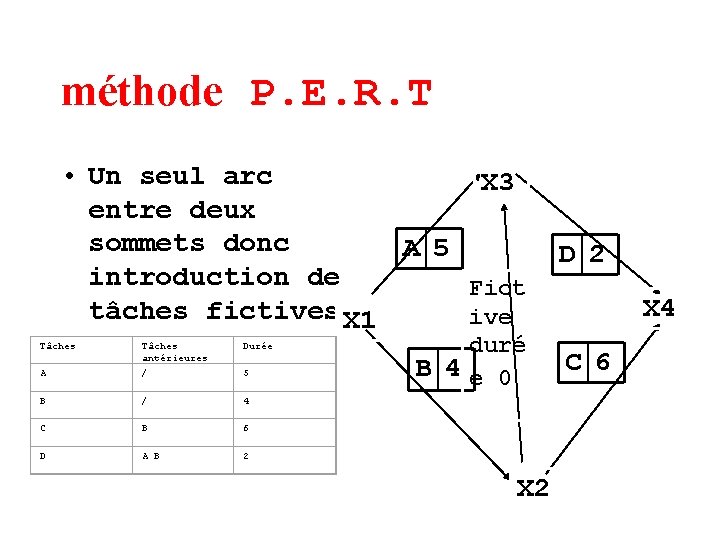
méthode P. E. R. T • Un seul arc X 3 entre deux sommets donc A 5 introduction de Fict tâches fictives X 1 ive Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2 duré B 4 e 0 X 2 D 2 X 4 C 6

b) La méthode M. P. M.

méthode M. P. M. • Chaque sommet représente une tâche. • A 5 B 4 D 2 C 6 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2

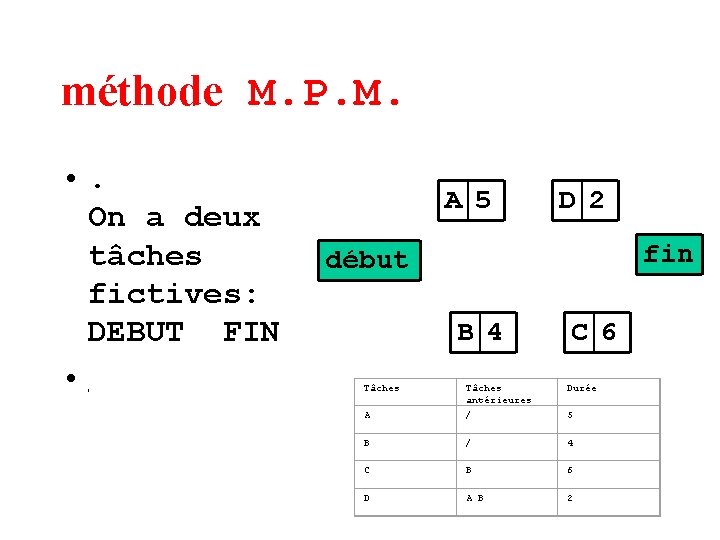
méthode M. P. M. • . On a deux tâches fictives: DEBUT FIN • A 5 D 2 fin début B 4 C 6 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2

méthode M. P. M. • Chaque sommet représente une tâche. début On a deux tâches fictives: DEBUT FIN • A 5 D 2 fin B 4 C 6 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2

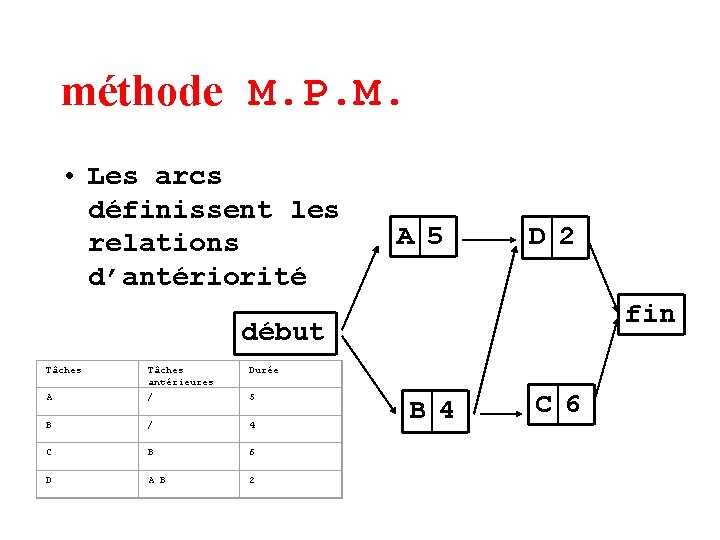
méthode M. P. M. • Les arcs définissent les relations d’antériorité A 5 D 2 fin début Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2 B 4 C 6

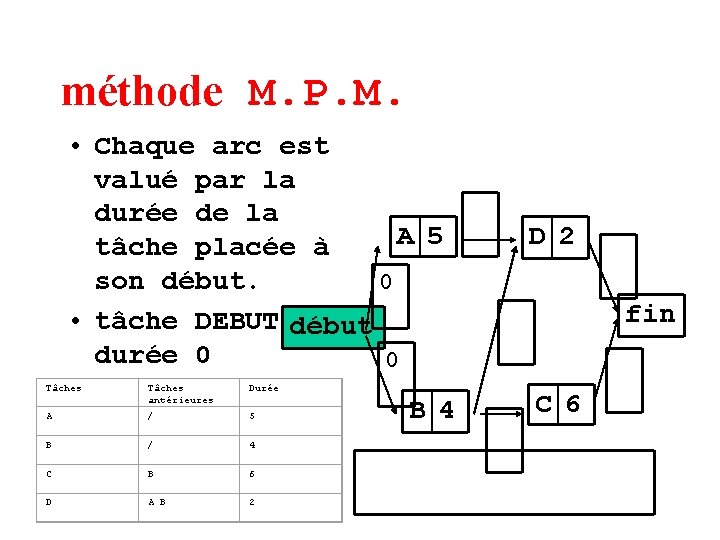
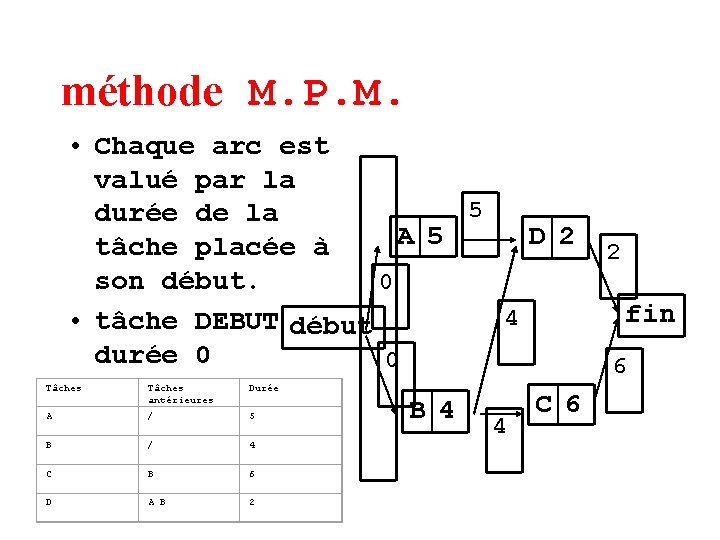
méthode M. P. M. • Chaque arc est valué par la durée de la A 5 tâche placée à son début. 0 • tâche DEBUT début durée 0 0 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2 B 4 D 2 fin C 6

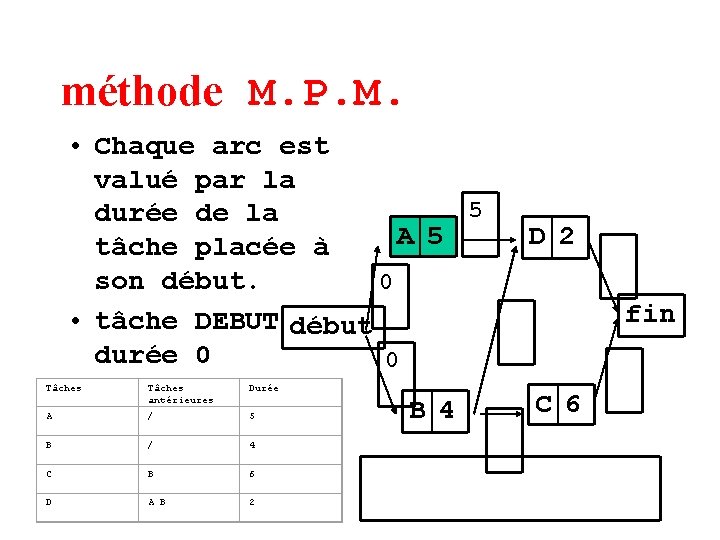
méthode M. P. M. • Chaque arc est valué par la 5 durée de la A 5 tâche placée à son début. 0 • tâche DEBUT début durée 0 0 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2 B 4 D 2 fin C 6

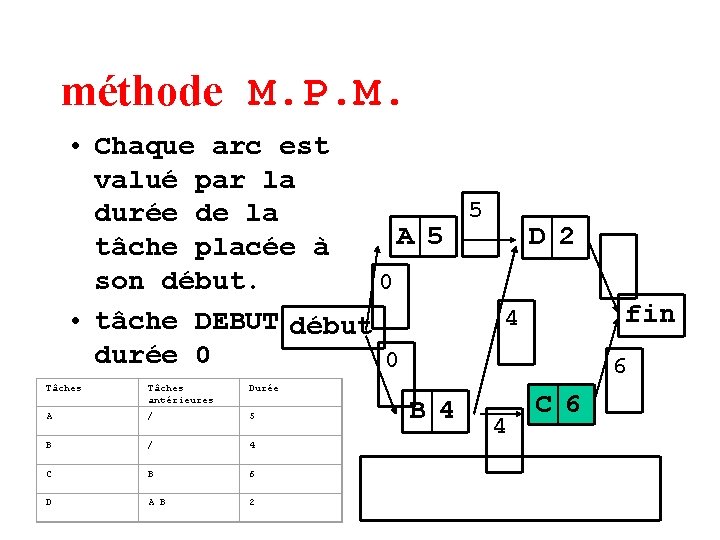
méthode M. P. M. • Chaque arc est valué par la 5 durée de la A 5 D 2 tâche placée à son début. 0 4 • tâche DEBUT début durée 0 0 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2 B 4 4 C 6 fin

méthode M. P. M. • Chaque arc est valué par la 5 durée de la A 5 D 2 tâche placée à son début. 0 4 • tâche DEBUT début durée 0 0 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2 B 4 4 C 6 fin 6

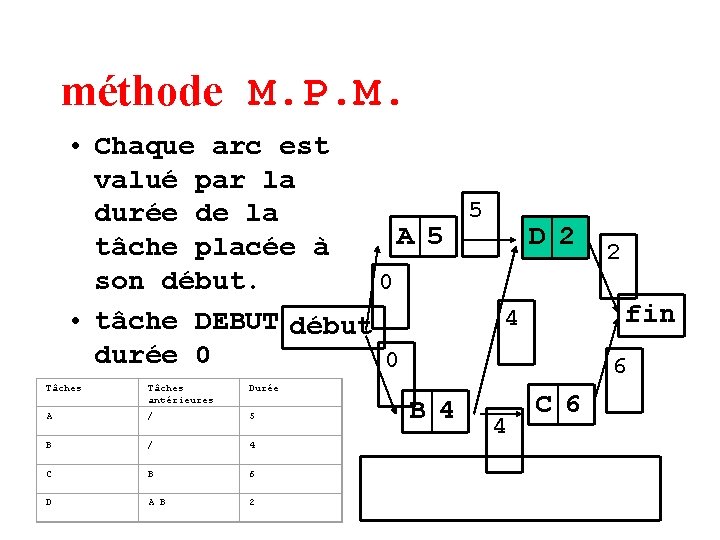
méthode M. P. M. • Chaque arc est valué par la 5 durée de la A 5 D 2 tâche placée à son début. 0 4 • tâche DEBUT début durée 0 0 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2 B 4 4 C 6 2 fin 6

méthode M. P. M. • Chaque arc est valué par la 5 durée de la A 5 D 2 tâche placée à son début. 0 4 • tâche DEBUT début durée 0 0 Tâches antérieures Durée A / 5 B / 4 C B 6 D A B 2 B 4 4 C 6 2 fin 6

4)DEFINITIONS ET AUTRES REPRESENTATIONS

• Si (x, y) U alors les sommets x et y sont adjacents, x est l’origine de l’arc et y l’extrémité. • x est un prédécesseur (précédent) d’y • y est un successeur (suivant) de x

• Un sommet c’est une sans prédécesseur entrée. sans successeur sortie.

Tableau ou dictionnaire des prédécesseurs sommets X 1 X 2 X 3 X 4 prédécesseurs

Tableau ou dictionnaire des prédécesseurs sommets prédécesseurs X 1 / X 2 X 1 X 3 X 1 X 2 X 4 X 2 X 3

sommets A B C D prédécesseurs

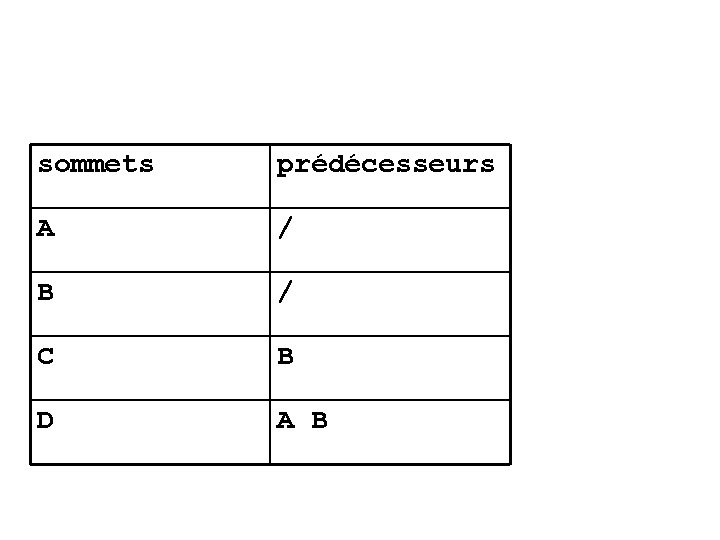
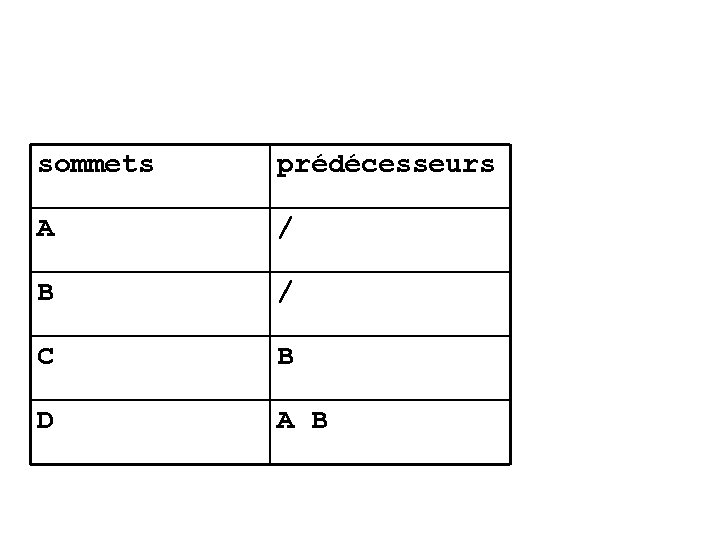
sommets prédécesseurs A / B / C B D A B

Tableau ou dictionnaire des successeurs sommets X 1 X 2 X 3 X 4 successeurs

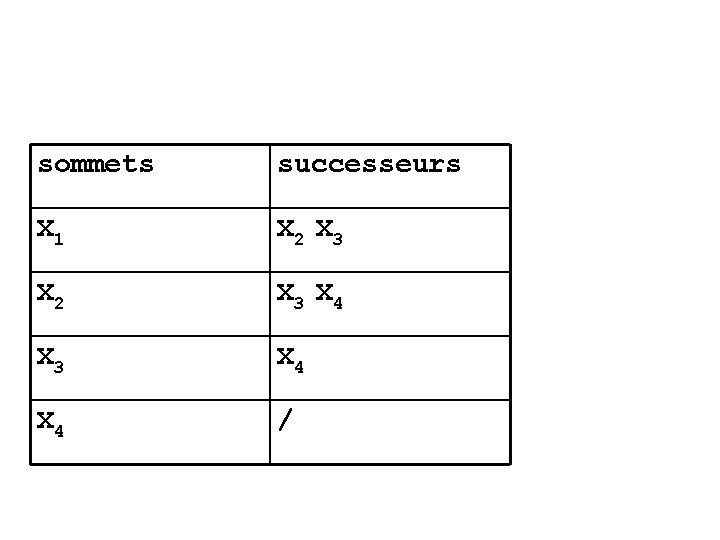
sommets successeurs X 1 X 2 X 3 X 4 /

sommets A B C D successeurs

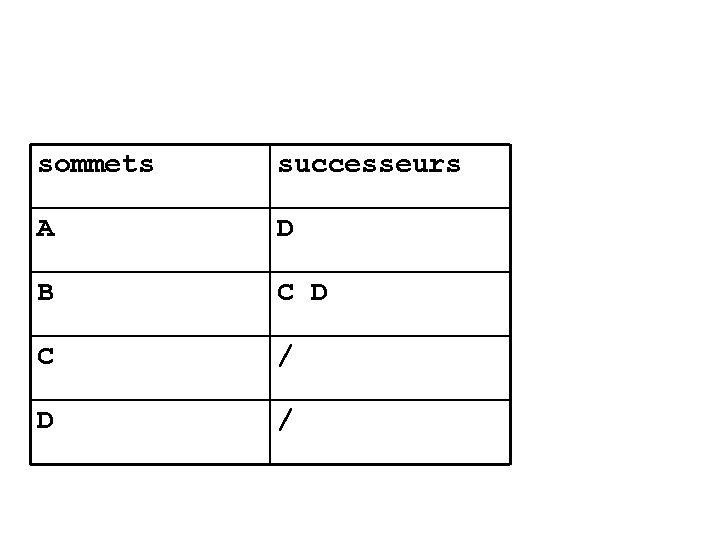
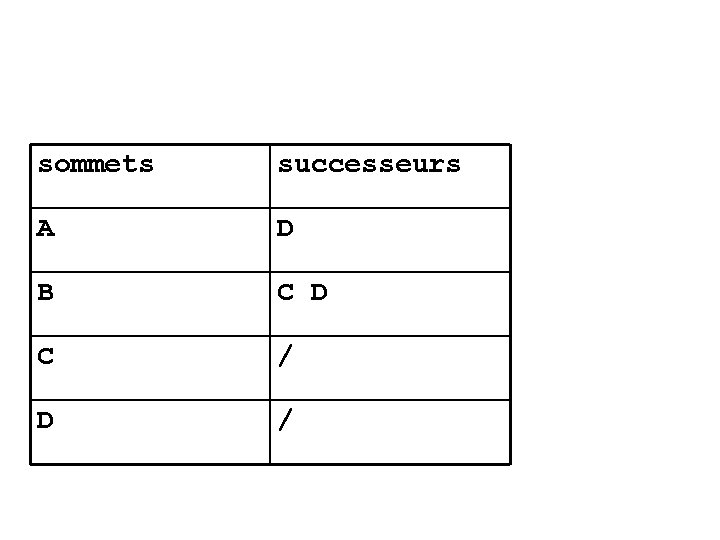
sommets successeurs A D B C D C / D /

Matrice adjacente ou booléenne A B 0 0 C D fin prsuc x 1 x 2 x 3 x 4 Début x 1 0 1 1 0 A x 2 0 0 1 1 B x 3 0 0 0 1 C 6 x 4 0 0 D 2 5 4 4 Dans un graphe valué on remplace les 1 par la valuation

5)ALGORITHME PERMETTANT D’OBTENIR LES NIVEAUX ( graphe sans circuit )

a) Définitions • Un chemin c’est une suite de points d’un graphe, telle que deux points qui se suivent sont reliés par un arc direct. • Ex: Chemins: ( x 1, x 3, x 4 ) ; ( x 1, x 2, x 3, x 4 ) N’est pas un chemin ( x 1, x 3, x 2 )

• Un circuit c’est un chemin non vide dont l’origine et l’extrémité sont confondus. • Une boucle c’est : (x, x) un arc

• La longueur d’un chemin ( au sens des arcs ) c’est le nombre d’arcs qu’il faut parcourir pour aller de l’origine à l’extrémité du chemin. • Ex: Le chemin longueur 3 ( x 1, x 2, x 3, x 4 ) est de

• Le niveau d’un la longueur du chemin au sens l’entrée et le • Ex: sommet x c’est plus long des arcs entre sommet x. x 3 est de niveau 2 et x 4 est de niveau 3

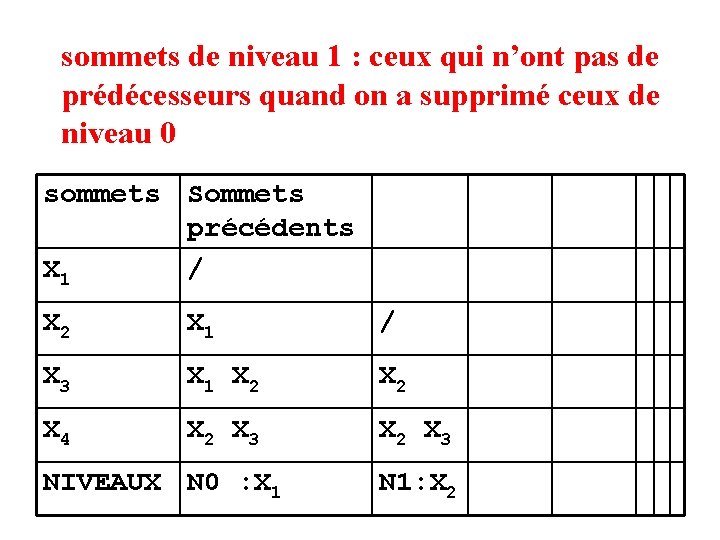
b) Recherche des niveaux • méthode : • sommets de niveau 0 : ceux qui n’ont pas de prédécesseurs. • sommets de niveau 1 : ceux qui n’ont pas de prédécesseurs quand on a supprimé ceux de niveau 0 , et ainsi de suite.

sommets de niveau 0 : ceux qui n’ont pas de prédécesseurs sommets Sommets précédents X 1 / X 2 X 1 X 3 X 1 X 2 X 4 X 2 X 3 NIVEAUX

sommets de niveau 0 : ceux qui n’ont pas de prédécesseurs sommets Sommets précédents X 1 / X 2 X 1 X 3 X 1 X 2 X 4 X 2 X 3 NIVEAUX N 0 : X 1

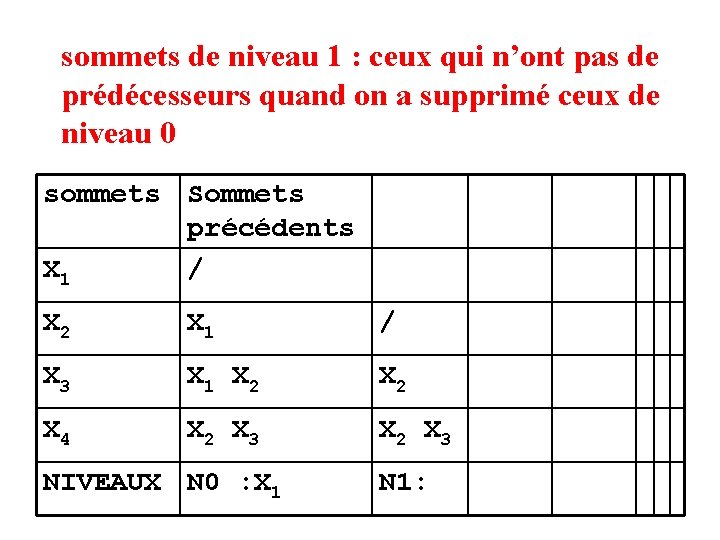
sommets de niveau 1 : ceux qui n’ont pas de prédécesseurs quand on a supprimé ceux de niveau 0 sommets Sommets précédents X 1 / X 2 X 1 / X 3 X 1 X 2 X 4 X 2 X 3 NIVEAUX N 0 : X 1 N 1:

sommets de niveau 1 : ceux qui n’ont pas de prédécesseurs quand on a supprimé ceux de niveau 0 sommets Sommets précédents X 1 / X 2 X 1 / X 3 X 1 X 2 X 4 X 2 X 3 NIVEAUX N 0 : X 1 N 1: X 2

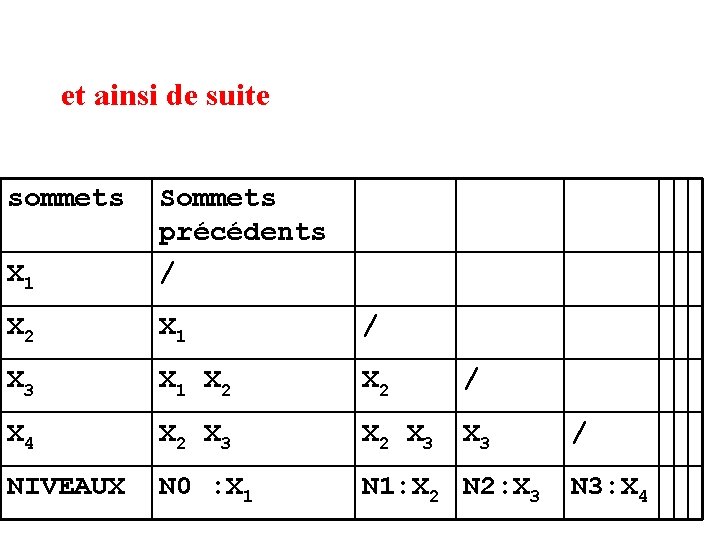
et ainsi de suite sommets Sommets précédents X 1 / X 2 X 1 / X 3 X 1 X 2 X 4 X 2 X 3 X 3 NIVEAUX N 0 : X 1 / N 1: X 2 N 2: X 3

et ainsi de suite sommets X 1 Sommets précédents / X 2 X 1 / X 3 X 1 X 2 / X 4 X 2 X 3 X 3 NIVEAUX N 0 : X 1 N 1: X 2 N 2: X 3 / N 3: X 4

sommets de niveau 0 : ceux qui n’ont pas de prédécesseurs Sommets A Sommets précédents / B / C B D A B NIVEAUX

sommets de niveau 0 : ceux qui n’ont pas de prédécesseurs Sommets A Sommets précédents / B / C B D A B NIVEAUX N 0 : A B

sommets de niveau 1 : ceux qui n’ont pas de prédécesseurs quand on a supprimé ceux de niveau 0 Sommets A Sommets précédents / B / C B / D A B / NIVEAUX N 0: A B N 1: C D

3)ALGORITHME PERMETTANT D’OBTENIR LE CHEMIN DE VALEUR OPTIMALE. Cas du MPM.

Exemple Tâches A Tâches Durée antérieures / 5 B / 4 C B 6 D A B 2

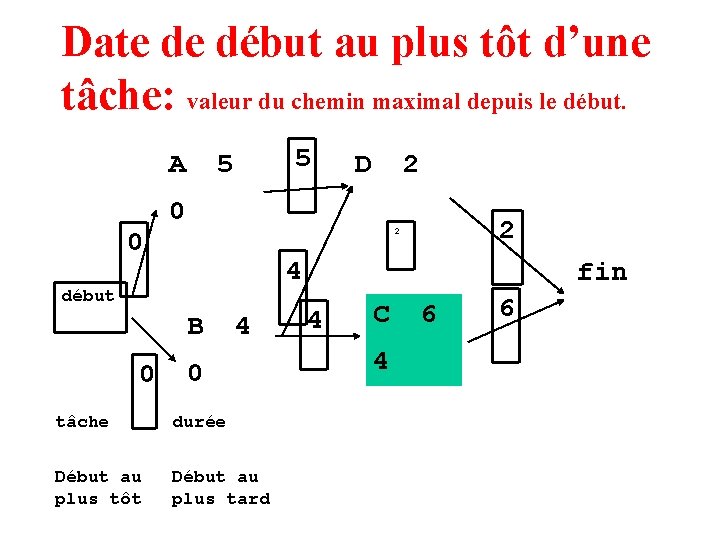
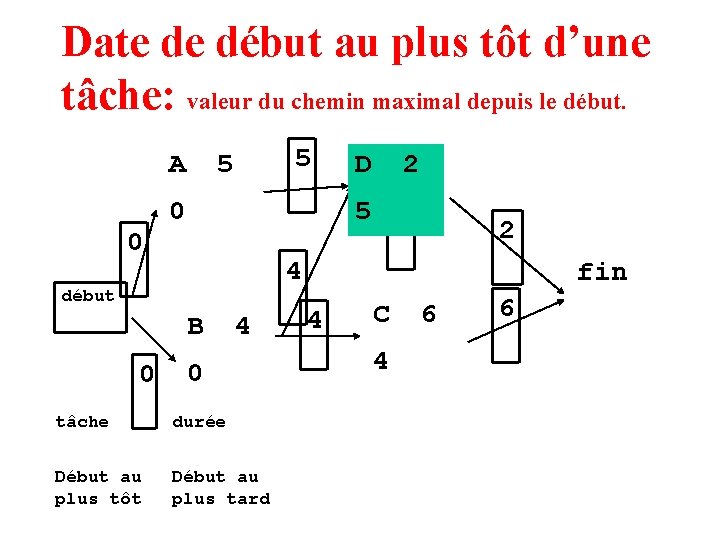
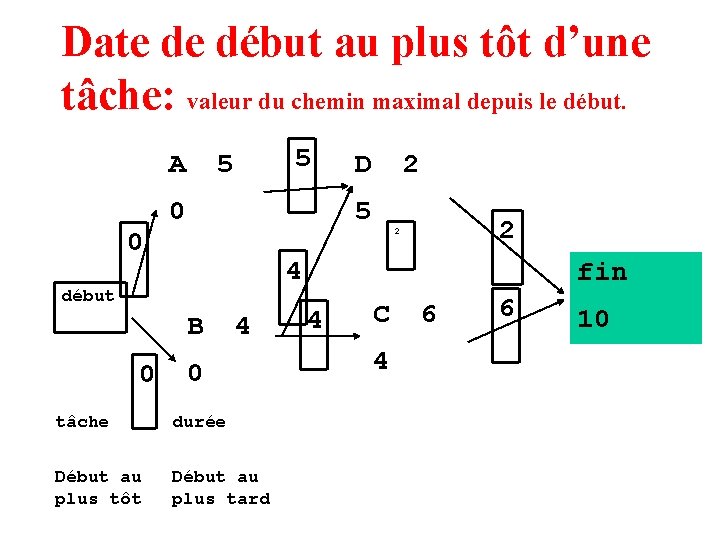
Date de début au plus tôt d’une tâche: valeur du chemin maximal depuis le début.

Date de début au plus tôt d’une tâche: valeur du chemin maximal depuis le début. A 0 5 5 2 0 2 2 4 début B 0 D 4 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 6 6

Date de début au plus tôt d’une tâche: valeur du chemin maximal depuis le début. A 0 5 5 2 0 2 2 4 début B 0 D 4 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 4 6 6

Date de début au plus tôt d’une tâche: valeur du chemin maximal depuis le début. A 0 5 5 0 2 5 2 2 4 début B 0 D 4 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 4 6 6

Date de début au plus tôt d’une tâche: valeur du chemin maximal depuis le début. A 0 5 5 0 2 5 2 2 4 début B 0 D 4 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 4 6 6 10

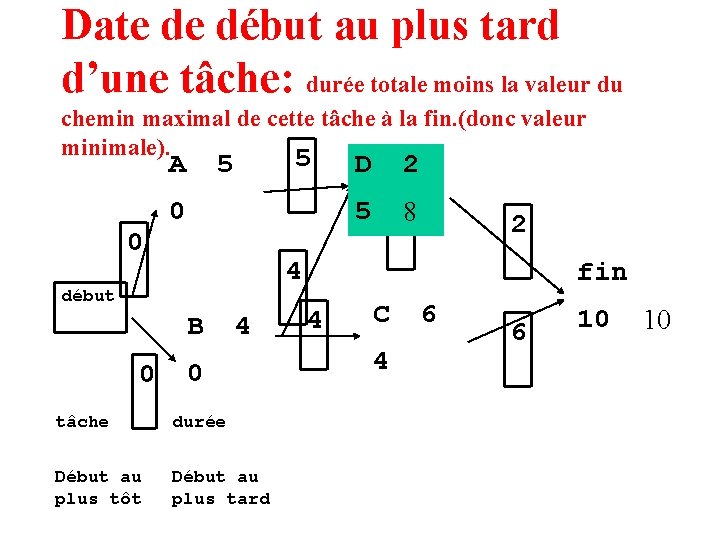
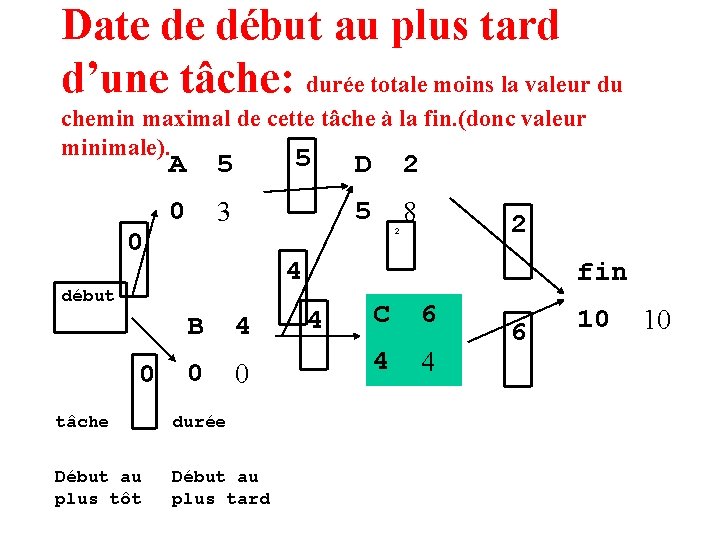
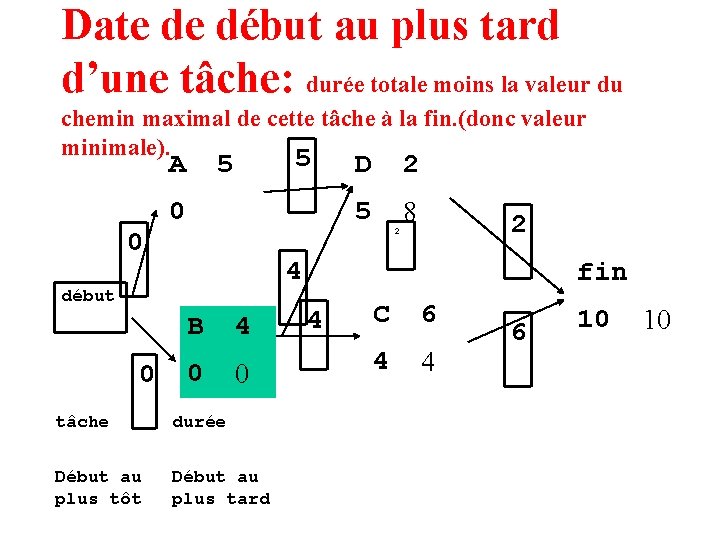
Date de début au plus tard d’une tâche: durée totale moins la valeur du chemin maximal de cette tâche à la fin. (donc valeur minimale).

Date de début au plus tard d’une tâche: durée totale moins la valeur du chemin maximal de cette tâche à la fin. (donc valeur minimale). 5 A 0 5 D 0 5 2 2 4 début B 0 2 4 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 4 6 6 10 10

Date de début au plus tard d’une tâche: durée totale moins la valeur du chemin maximal de cette tâche à la fin. (donc valeur minimale). 5 A 0 5 D 0 5 2 8 2 4 début B 0 2 4 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 4 6 6 10 10

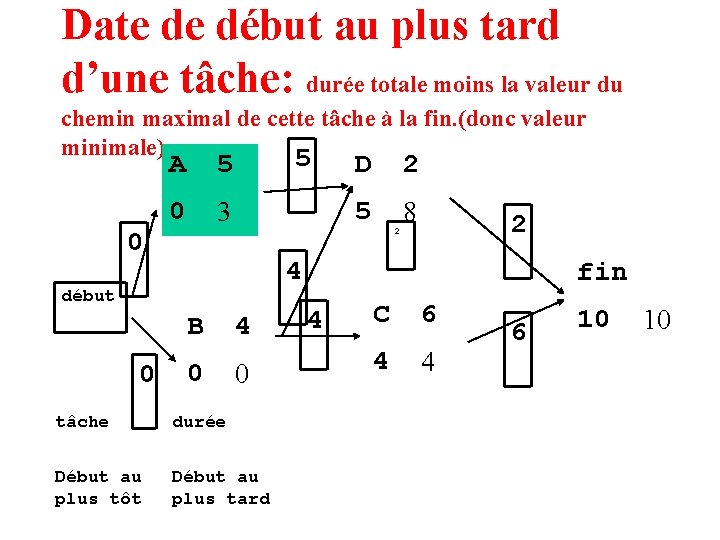
Date de début au plus tard d’une tâche: durée totale moins la valeur du chemin maximal de cette tâche à la fin. (donc valeur minimale). 5 0 A 5 D 0 3 5 2 8 2 4 début 0 2 B 4 0 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 6 4 4 6 10 10

Date de début au plus tard d’une tâche: durée totale moins la valeur du chemin maximal de cette tâche à la fin. (donc valeur minimale). 5 A 0 5 D 0 5 2 8 2 4 début 0 2 B 4 0 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 6 4 4 6 10 10

Date de début au plus tard d’une tâche: durée totale moins la valeur du chemin maximal de cette tâche à la fin. (donc valeur minimale). 5 0 A 5 D 0 3 5 2 8 2 4 début 0 2 B 4 0 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 6 4 4 6 10 10

Graphe M. P. M. 0 A 5 0 3 5 2 8 2 4 début 0 D B 4 0 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 6 4 4 6 10 10

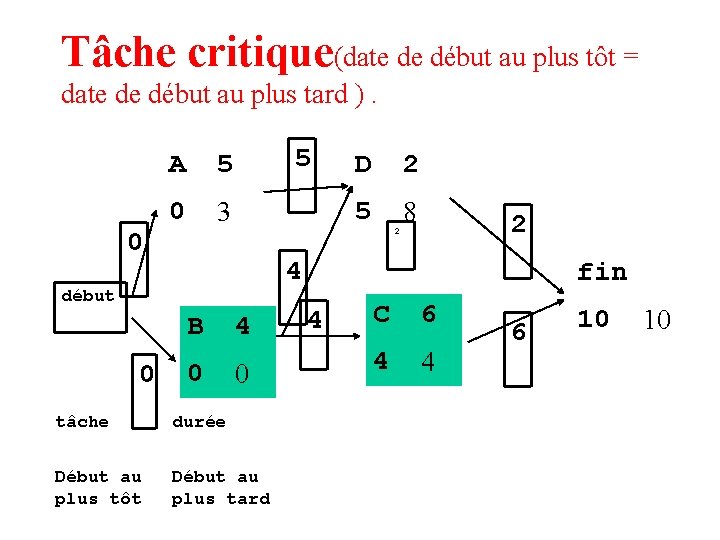
Tâche critique • Une tâche est critique si tout retard apporté à son début au plus tôt retarde la date de fin au plus tôt du projet (date de début au plus tôt = date de début au plus tard ).

Tâche critique(date de début au plus tôt = date de début au plus tard ). 0 A 5 0 3 5 2 8 2 4 début 0 D B 4 0 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 6 4 4 6 10 10

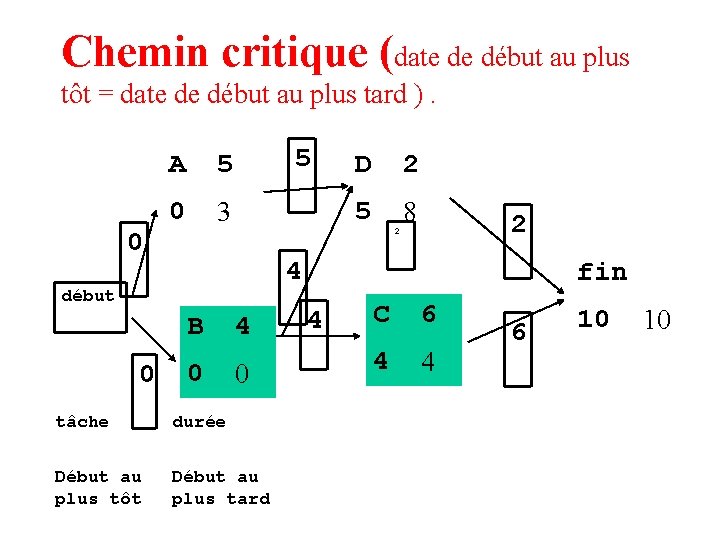
Chemin critique • Chemin critique : il est formé des tâches critiques • Une tâche est critique si tout retard apporté à son début au plus tôt retarde la date de fin au plus tôt du projet (date de début au plus tôt = date de début au plus tard ).

Chemin critique (date de début au plus tôt = date de début au plus tard ). 0 A 5 0 3 5 2 8 2 4 début 0 D B 4 0 0 tâche durée Début au plus tôt Début au plus tard fin 4 C 6 4 4 6 10 10

Marges

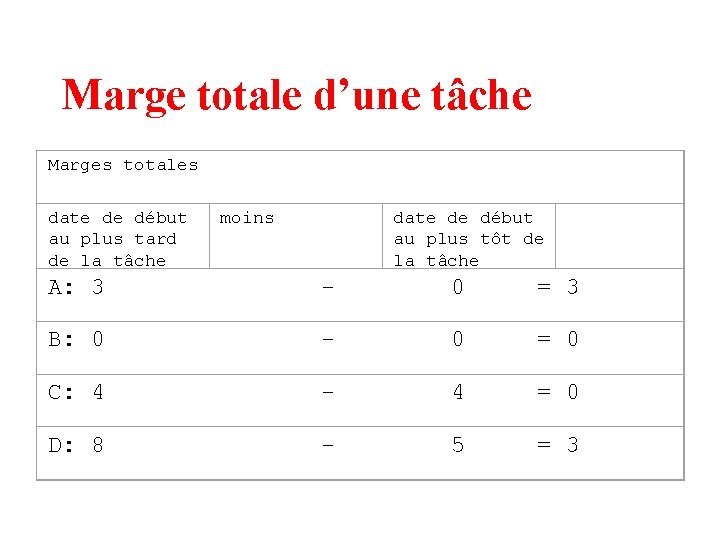
Marge totale d’une tâche • le retard maximal que l’on peut admettre au démarrage d’une tâche sans remettre en cause la durée du projet. • (date de début au plus tard de la tâche)-( date de début au plus tôt de la tâche)

Marge totale d’une tâche Marges totales date de début au plus tard de la tâche moins date de début au plus tôt de la tâche A: 3 - 0 = 3 B: 0 - 0 = 0 C: 4 - 4 = 0 D: 8 - 5 = 3

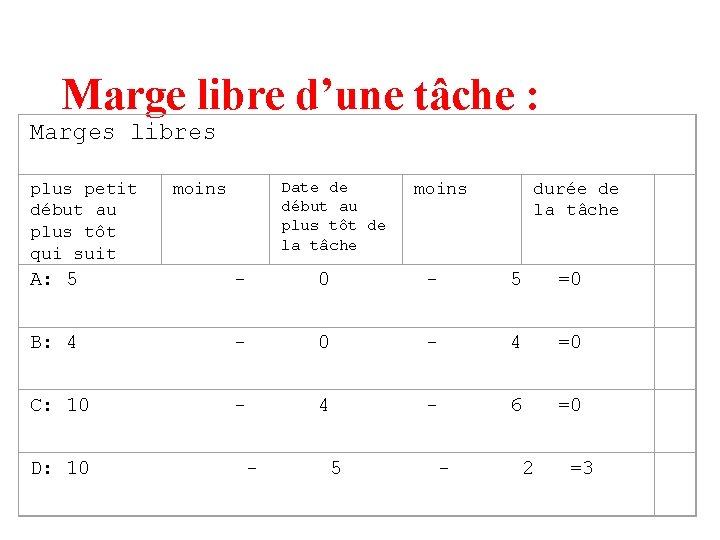
Marge libre d’une tâche : • le retard maximal que l’on peut admettre au démarrage d’une tâche sans remettre en cause le début au plus tôt des tâches suivantes. • (plus petit début au plus tôt qui suit)-(Date de début au plus tôt de la tâche)-(durée de la tâche))

Marge libre d’une tâche : Marges libres plus petit début au plus tôt qui suit Date de début au plus tôt de la tâche moins durée de la tâche A: 5 - 0 - 5 =0 B: 4 - 0 - 4 =0 C: 10 - 4 - 6 =0 D: 10 - 5 - 2 =3

• fin

6)ALGORITHME PERMETTANT D’OBTENIR LES CHEMINS DE LONGUEUR p

a) Définitions • Un chemin c’est une suite de points d’un graphe, telle que deux points qui se suivent sont reliés par un arc direct. • Ex:

• La longueur d’un chemin ( au sens des arcs ) c’est le nombre d’arcs qu’il faut parcourir pour aller de l’origine à l’extrémité du chemin. • Ex:

b)Propriété • Soit M la Matrice adjacente ou booléenne d’un graphe et soit Mp =(ci, j) la puissance p de M • • alors ci, j est le nombre de chemins de longueur p allant du sommet i au sommet j.

c)Remarques • Soit n le nombre de sommets • Si Mn 0 le graphe contient des circuits et si le terme diagonal ai, i 0 il existe au moins un chemin de longueur n de i à i (c’est à dire un circuit ) •

c)Remarques • Soit n le nombre de sommets • Si Mn 0 le graphe contient des circuits et si le terme diagonal ai, i 0 il existe au moins un chemin de longueur n de i à i (c’est à dire un circuit ) • • Les colonnes de zéros de Mn permettent de retrouver les nivaux.

c)Remarques • Soit n le nombre de sommets • Si Mn 0 le graphe contient des circuits et si le terme diagonal ai, i 0 il existe au moins un chemin de longueur n de i à i (c’est à dire un circuit ) • • Les colonnes de zéros de Mn permettent de retrouver les nivaux.

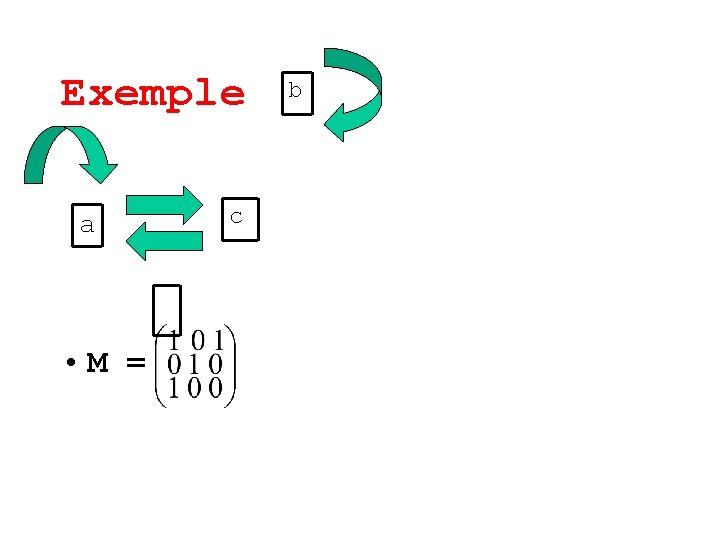
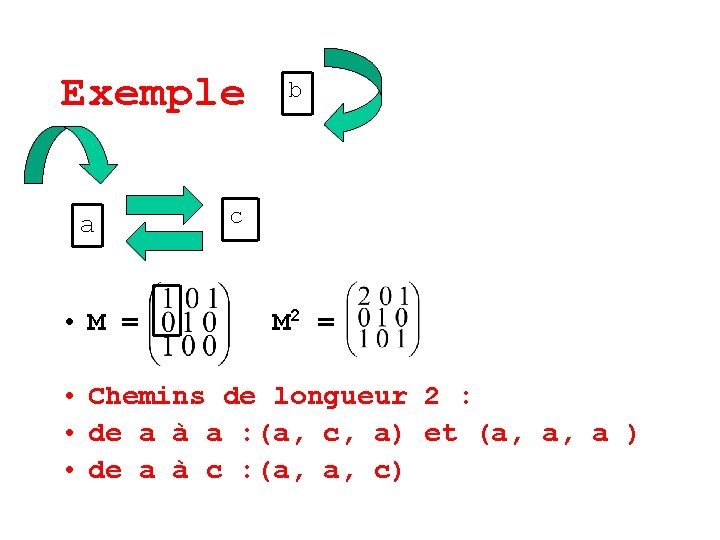
Exemple a • M = c b

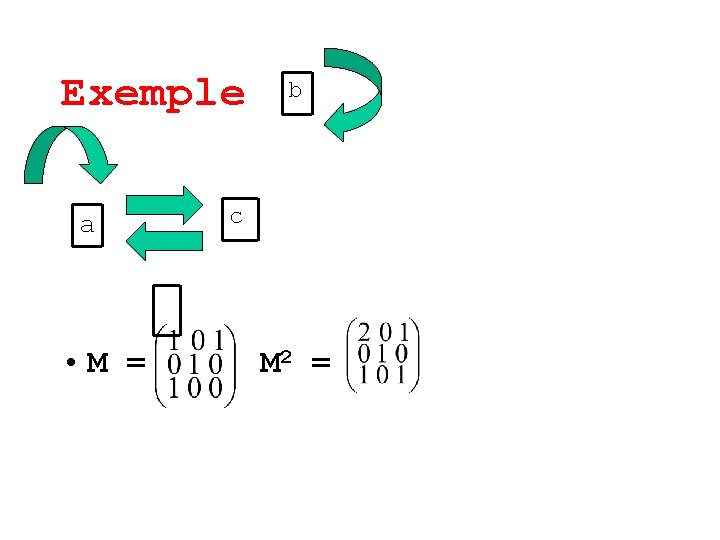
Exemple a • M = b c M 2 =

Exemple a • M = b c M 2 = • Chemins de longueur 2 : • de a à a : (a, c, a) et (a, a, a ) • de a à c : (a, a, c)

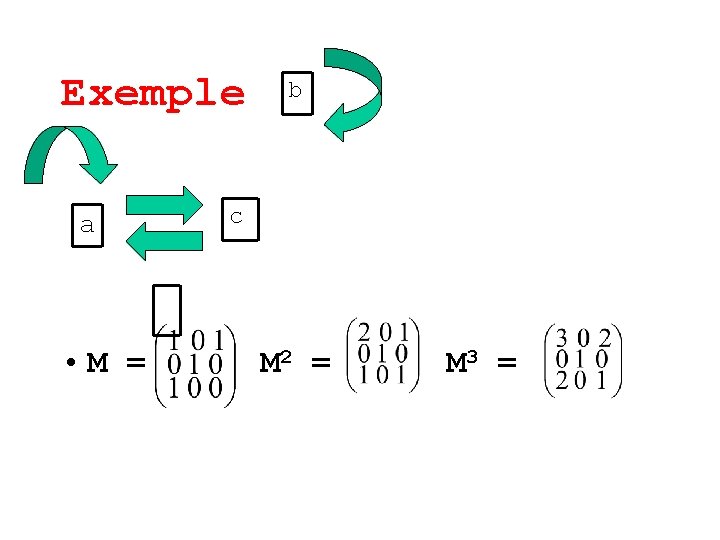
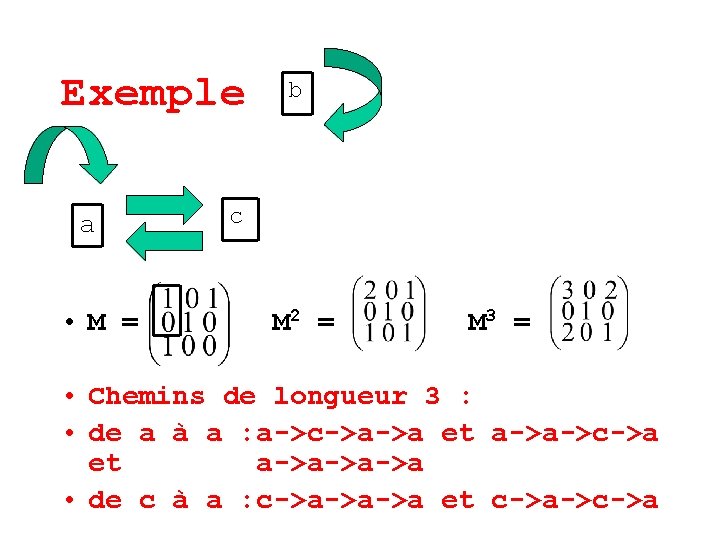
Exemple a • M = b c M 2 = M 3 =

Exemple a • M = b c M 2 = M 3 = • Chemins de longueur 3 : • de a à a : a->c->a->a et a->a->c->a et a->a->a->a • de c à a : c->a->a->a et c->a->c->a

7) ALGORITHME PERMETTANT D’OBTENIR LA FERMETURE TRANSITIVE.

A) Opérations sur les relations • a)Union • Soit R et R’ deux relations sur un ensemble E, leur réunion R R’ c’est la relation dont le graphe est la réunion des arcs de R et de R’. • Exemple

R R’ b a • M= c R R’ b a M’= b a c M M’ = Somme Booléenne La matrice de R R’ c’est M M’ c

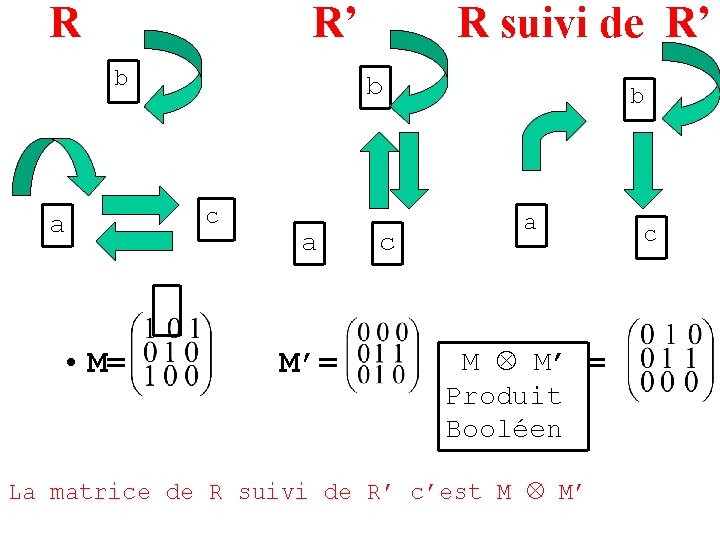
b)composition : R suivi de R’

R R’ b a • M= R suivi de R’ b c a M’= c b a M M’ = Produit Booléen La matrice de R suivi de R’ c’est M M’ c

B) Fermeture transitive de R : • Transitivité • Une relation est transitive si : • ( x)( y)( z) • (( x. Ry et y. Rz ) x. Rz )

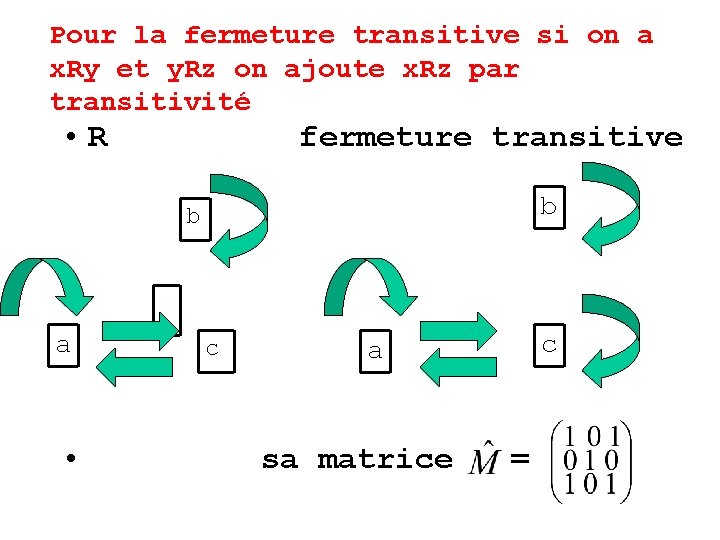
Pour la fermeture transitive si on a x. Ry et y. Rz on ajoute x. Rz par transitivité • R fermeture transitive b b a • c c a sa matrice =

• Remarque : • La matrice de la fermeture transitive est = M M[2] M[3] M[4] +……

• fin

3)DEFINITIONS ET AUTRES REPRESENTATIONS

• Si (x, y) U alors les sommets x et y sont adjacents, x est l’origine de l’arc et y l’extrémité. • x est un prédécesseur (précédent) d’y • y est un successeur (suivant) de x

• Un sommet c’est une sans prédécesseur entrée. sans successeur sortie.

Tableau ou dictionnaire des prédécesseurs

sommets X 1 X 2 X 3 X 4 prédécesseurs

sommets prédécesseurs X 1 / X 2 X 1 X 3 X 1 X 2 X 4 X 2 X 3

sommets A B C D prédécesseurs

sommets prédécesseurs A / B / C B D A B

Tableau ou dictionnaire des successeurs

sommets X 1 X 2 X 3 X 4 successeurs

sommets successeurs X 1 X 2 X 3 X 4 /

sommets A B C D successeurs

sommets successeurs A D B C D C / D /


Matrice adjacente ou booléenne
 Graphe nombre chromatique
Graphe nombre chromatique Graphe bible college
Graphe bible college Graphe complet
Graphe complet Graphe des interacteurs
Graphe des interacteurs Theorie des graphe
Theorie des graphe Drawing with light greek
Drawing with light greek Classe d'équivalence coupe tube
Classe d'équivalence coupe tube Cocycle graphe
Cocycle graphe Rayon d'un graphe snt
Rayon d'un graphe snt Orient ezan cihazı
Orient ezan cihazı Orient express útvonal
Orient express útvonal Murder on the orient express analysis
Murder on the orient express analysis Land nav basics
Land nav basics Lensatic definition
Lensatic definition Orient east med corridor
Orient east med corridor Orient east med corridor
Orient east med corridor Orient east med corridor
Orient east med corridor Murder on the orient express analysis
Murder on the orient express analysis Ministry of transport, communications and works
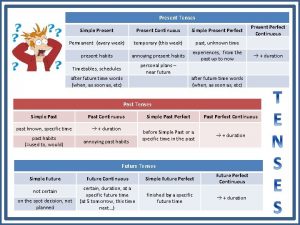
Ministry of transport, communications and works Present simple past simple future simple test
Present simple past simple future simple test Simple past simple present simple future
Simple past simple present simple future Past continuous present simple
Past continuous present simple Present continuous past continuous future continuous
Present continuous past continuous future continuous Present simple, past simple, future simple
Present simple, past simple, future simple Present simple past simple present continuous exercises
Present simple past simple present continuous exercises Present past future simple
Present past future simple Present perfect tense
Present perfect tense Future simple present simple
Future simple present simple Les parts de la flor
Les parts de la flor Les lettres et les sons
Les lettres et les sons Le volcan le plus dangereux du monde
Le volcan le plus dangereux du monde La fiche de lecture de la ficelle
La fiche de lecture de la ficelle Les constellations les plus connues
Les constellations les plus connues Je moi tu toi
Je moi tu toi Part de la planta en la fulla s'uneix a la tija
Part de la planta en la fulla s'uneix a la tija Mot invariable et variable
Mot invariable et variable Les mots variable
Les mots variable Trouvez les réponses. écrivez-les en chiffres (numbers).
Trouvez les réponses. écrivez-les en chiffres (numbers). Les trains grand corps malade
Les trains grand corps malade Allez vous en sur les places et sur les parvis
Allez vous en sur les places et sur les parvis Preactionneurs
Preactionneurs Les trois obstacles et les quatre démons
Les trois obstacles et les quatre démons Cherchez d'abord le royaume de dieu lyrics
Cherchez d'abord le royaume de dieu lyrics Horloge de bowman
Horloge de bowman Qu'est-ce que tu aimes manger?
Qu'est-ce que tu aimes manger? Les mots qu'on ne dit pas sont les fleurs du silence
Les mots qu'on ne dit pas sont les fleurs du silence Organisateur textuel de succession
Organisateur textuel de succession Cestbeaulavie
Cestbeaulavie Exemple de texte expressif
Exemple de texte expressif Fonctions techniques et solutions techniques
Fonctions techniques et solutions techniques Les voitures les plus rapides du monde
Les voitures les plus rapides du monde Describe present tense
Describe present tense Courirai
Courirai Roue et axe machine simple
Roue et axe machine simple Grille 14 besoins de virginia henderson
Grille 14 besoins de virginia henderson Adverbe c'est quoi
Adverbe c'est quoi Les soins relationnels définition
Les soins relationnels définition Constructing simple electrical gadgets ppt
Constructing simple electrical gadgets ppt X simple and y simple
X simple and y simple Simple predicate
Simple predicate Likedrome
Likedrome Simple present tense plural
Simple present tense plural Past perfect past simple and past continuous
Past perfect past simple and past continuous Signaalwoorden past simple
Signaalwoorden past simple The present simple passive
The present simple passive Diferencia entre pasado simple y presente perfecto
Diferencia entre pasado simple y presente perfecto Simple discount note
Simple discount note Question present simple passive
Question present simple passive Dress simple past
Dress simple past Simple present function
Simple present function Present simple present continuous past simple
Present simple present continuous past simple Knit past form
Knit past form Present simple past simple
Present simple past simple Study present simple
Study present simple Simple present present progressive simple past
Simple present present progressive simple past If present simple present simple
If present simple present simple Simple past vs simple present
Simple past vs simple present Past indefinite tense
Past indefinite tense Yesterday present simple
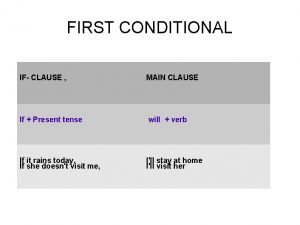
Yesterday present simple First conditional present continuous
First conditional present continuous Direct and reported speech examples
Direct and reported speech examples Simple subject examples
Simple subject examples Present simple tense verb
Present simple tense verb What is simple subject and simple predicate
What is simple subject and simple predicate Simple subject and simple predicate
Simple subject and simple predicate The past of be
The past of be Simple predicate
Simple predicate Present simple negative
Present simple negative Present simple present progressive past simple
Present simple present progressive past simple Passive voice simple present
Passive voice simple present Present simple present progressive past simple
Present simple present progressive past simple Simple discount rate formula
Simple discount rate formula Past perfect simple vs past perfect continuous
Past perfect simple vs past perfect continuous Secularism means
Secularism means What is democracy
What is democracy Definition dystopian society
Definition dystopian society Pictures of warm fronts
Pictures of warm fronts Name a multicellular organism
Name a multicellular organism Define present perfect tense
Define present perfect tense Coagulation eggs definition
Coagulation eggs definition Group polarization in mean girls
Group polarization in mean girls Probability definition
Probability definition A slingshot consists of a light leather cup
A slingshot consists of a light leather cup Simple sentence definition
Simple sentence definition Elastic clause definition
Elastic clause definition Given: the 420 n force along the cable ac.
Given: the 420 n force along the cable ac. Air pollution consequences
Air pollution consequences Ozone layer simple definition
Ozone layer simple definition Pleitropy
Pleitropy Literary terms allusion
Literary terms allusion Mercantilism definition world history
Mercantilism definition world history Codominance definition
Codominance definition