Les Fractales Flocon de Von Koch Cette courbe

Les Fractales Flocon de Von Koch Cette « courbe » s'obtient en appliquant à chaque côté d'un triangle équilatéral une transformation simple : on remplace le 1/3 central de chaque côté par 2 segments ayant la même longueur que celle qui a été prélevée et on recommence la même opération sur chaque côté de la figure obtenue. On obtient une surface de dimension finie qui est limitée par une frontière de longueur infinie. 1

Les Fractales Flocon de Von Koch Question : sauriez-vous démontrer que cette surface tend vers a étant la longueur du côté du triangle initial ? 2

Les Fractales Les fractales naturelles 3

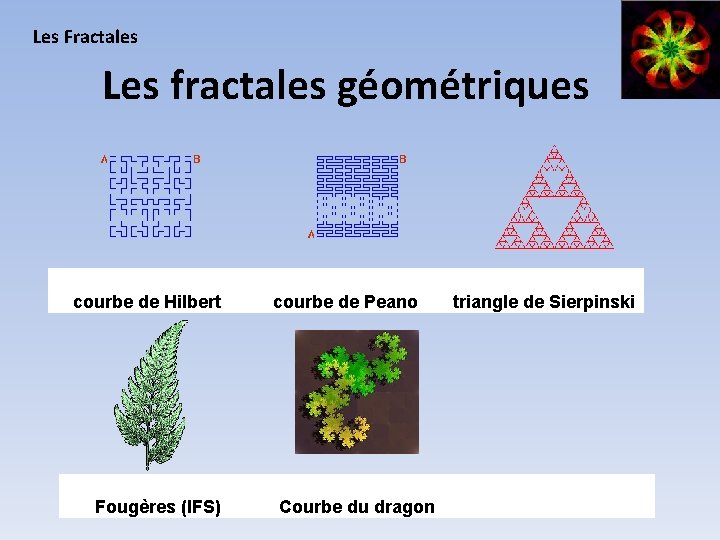
Les Fractales Les fractales géométriques courbe de Hilbert Fougères (IFS) courbe de Peano Courbe du dragon triangle de Sierpinski 4

Les Fractales Les nombres complexes Le plus simple des polynômes complexes étudiés ainsi est P(z)=z 2+c ce qui conduit à la suite : zn+1=zn 2+c Que constate-t-on alors ? Pour certaines valeurs de départ de z le résultat se maintient au fil de itérations successives dans un intervalle bien limité. Au contraire pour d'autres valeurs la fonction diverge et le point représentant le résultat s'échappe vers l'infini. 5

Les Fractales Les nombres complexes : partie réelle de c = -0. 0519. . . partie imaginaire = 0. 688. . . Ensemble de Julia connexe. partie réelle de c = -0. 577. . . partie imaginaire = 0. 478. . . Ensemble de Julia non connexe. 6

Les Fractales Les nombres complexes Détail d'un ensemble de Julia. 7

Les Fractales Les nombres complexes L'ensemble de Mandelbrot Dans la formule de récurrence : zn+1=zn 2+c, on fixe z 0 = 0 et on fait varier c Dans le plan complexe. 8

Les Fractales Les quaternions sont une généralisation des nombres complexes. Les quaternions ont une partie entière et trois parties imaginaires. Si les ensembles de Mandelbrot et de Julia classiques peuvent être représentés en deux dimensions, leurs homologues quaternioniques ont quatre dimensions. Les choses sont toutefois plus simples qu'il n'y paraît. En effet on peut considérer ces objets comme des objets à trois dimensions qui évoluent dans le temps (la quatrième dimension). Lien Wikipédia vers La définition mathématiques Des quaternions 9

Les Fractales Les quaternions sont une généralisation des nombres complexes. Les quaternions ont une partie entière et trois parties imaginaires. Si les ensembles de Mandelbrot et de Julia classiques peuvent être représentés en deux dimensions, leurs homologues quaternioniques ont quatre dimensions. Les choses sont toutefois plus simples qu'il n'y paraît. En effet on peut considérer ces objets comme des objets à trois dimensions qui évoluent dans le temps (la quatrième dimension). 10

Les Fractales Le mandel. Bulb Lien vers un site du CNRS 11

Les Fractales La Mandel. Box Lien vers un site du CNRS 12

Les Fractales Les paysages fractals la méthode de déplacement du point médian. Une surface plane est découpée en plusieurs parties par un maillage (carré par exemple) et un déplacement vertical aléatoire est appliqué au centre de chaque maille. Chaque partie est à sont tour subdivisée en surfaces plus petites par le même mécanisme et on applique au centre de chacune d'elles un nouveau déplacement vertical aléatoire. On recommence un nombre suffisant de fois pour avoir des détails de taille assez petite afin que l'image soit réaliste. Exemple de paysage obtenu très facilement avec le programme Terragen. 13

Les Fractales Les paysages fractals méthode plus élaborée repose sur l'utilisation d'une fonction décrivant un mouvement brownien fractionnaire. Exemple de paysage obtenu très facilement avec le programme Terragen. 14

Les Fractales A quoi servent les fractales ? • Etude des cours boursiers • Structure de l’univers • Etude de la percolation (compagnies pétrolières) • Etude des bruits parasites dans les circuits électroniques • Compression d’images • Fabrication d’antennes radio fractales • Et bien d’autres domaines …. . 15