Les CONIQUES Les 4 coniques Cercle Ellipse Parabole

Les CONIQUES
Les 4 coniques Cercle Ellipse Parabole Hyperbole Proviennent de la coupe du cône. C’est la forme de la section.
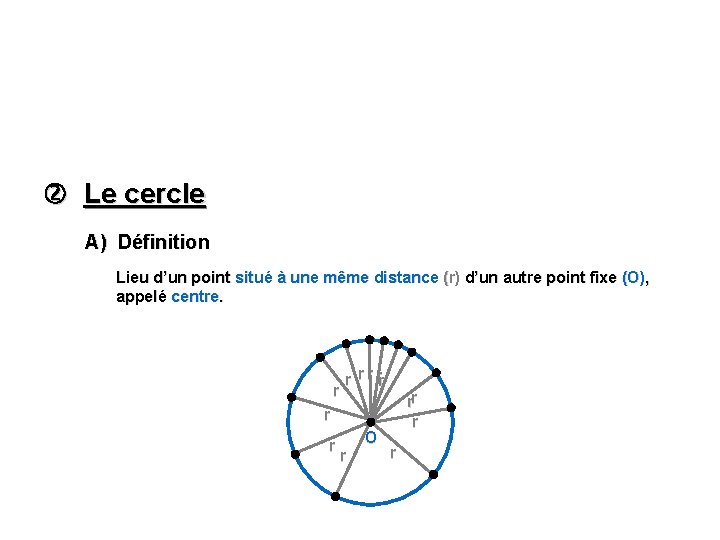
Le cercle A) Définition Lieu d’un point situé à une même distance (r) d’un autre point fixe (O), appelé centre. r r rr rr r r O r
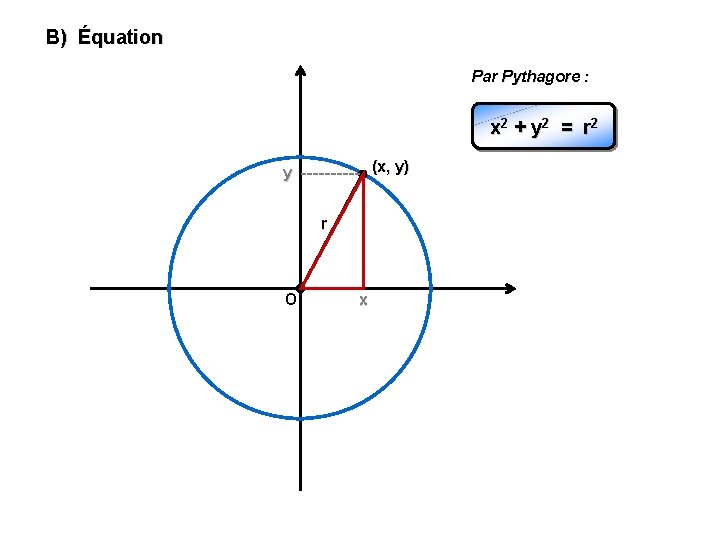
B) Équation Par Pythagore : x 2 + y 2 = r 2 (x, y) y r O x
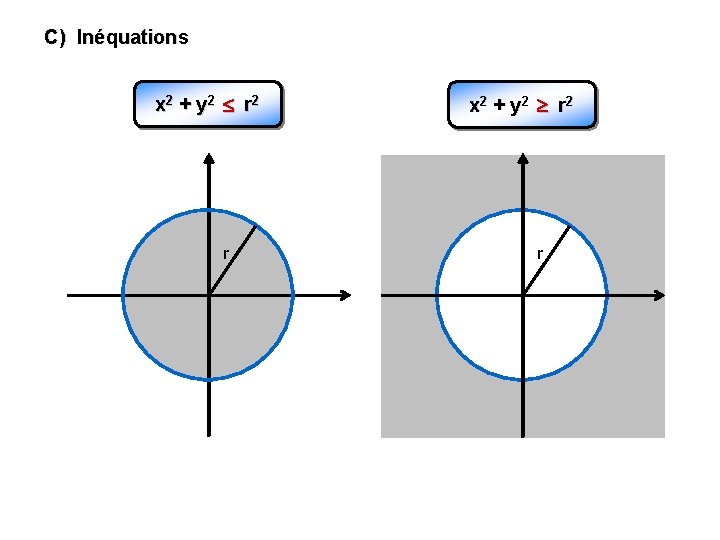
C) Inéquations x 2 + y 2 r 2 r
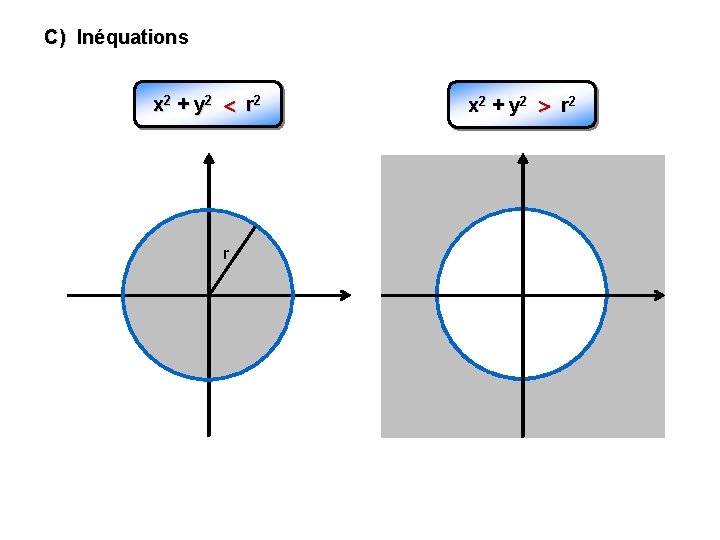
C) Inéquations x 2 + y 2 r 2 r
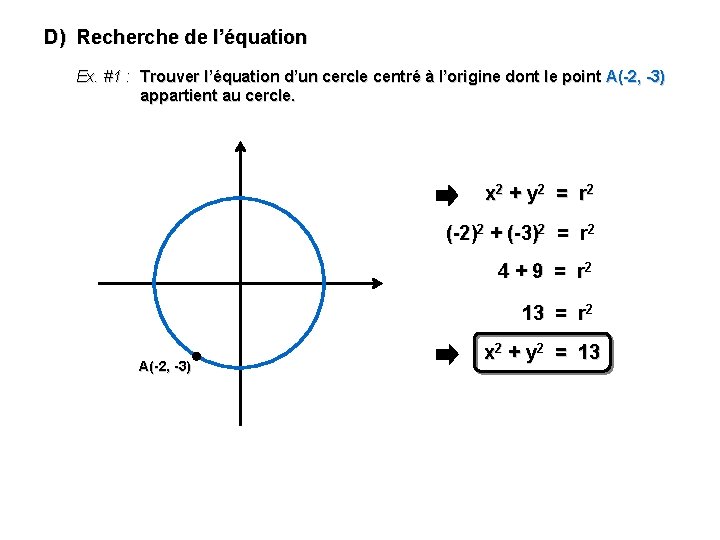
D) Recherche de l’équation Ex. #1 : Trouver l’équation d’un cercle centré à l’origine dont le point A(-2, -3) appartient au cercle. x 2 + y 2 = r 2 (-2)2 + (-3)2 = r 2 4 + 9 = r 2 13 = r 2 A(-2, -3) x 2 + y 2 = 13

D) Recherche de l’équation Ex. #2 : a) Quelle est l’équation d’un cercle centré à l’origine dont le diamètre est de 16 unités ? Le rayon est de 8 unités. x 2 + y 2 = 8 2 x 2 + y 2 = 64 b) Est-ce que le point P(5, 7) fait partie de la région intérieure de ce cercle ? Il faut que l’inégalité 52 + 72 64 soit VRAIE. 25 + 49 64 74 64 FAUX ! Le point P(5, 7) ne fait pas partie de la région intérieure de ce cercle.
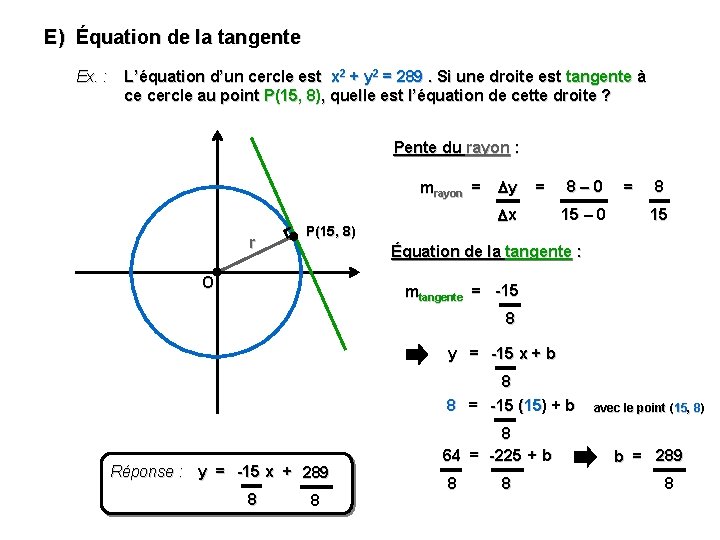
E) Équation de la tangente Ex. : L’équation d’un cercle est x 2 + y 2 = 289. Si une droite est tangente à ce cercle au point P(15, 8), quelle est l’équation de cette droite ? Pente du rayon : mrayon = r y = x P(15, 8) 8– 0 15 – 0 = 8 15 Équation de la tangente : O mtangente = -15 8 y = -15 x + b 8 8 = -15 (15) + b Réponse : y = -15 x + 289 8 8 8 64 = -225 + b 8 8 avec le point (15, , 8) 8) b = 289 8

L’ellipse A) Définition Lieu d’un point dont la somme des distances à deux points fixes (foyers F et F’) est constante (k).
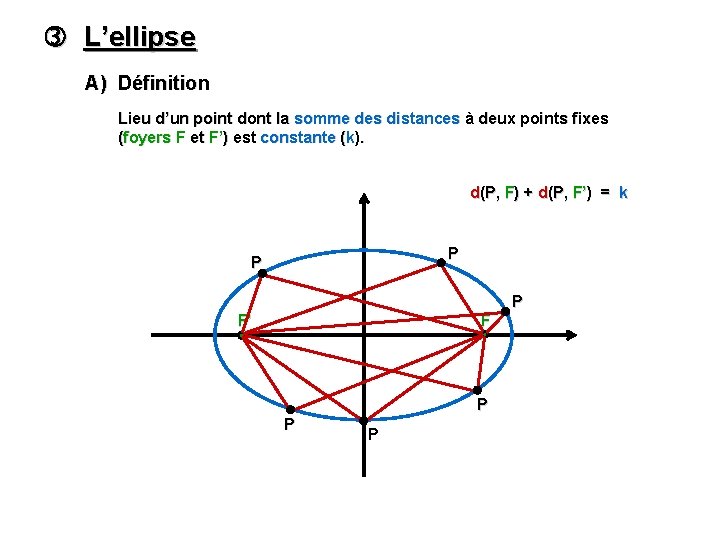
L’ellipse A) Définition Lieu d’un point dont la somme des distances à deux points fixes (foyers F et F’) est constante (k). d(P, F) + d(P, F’) = k P P P F’ F P P P
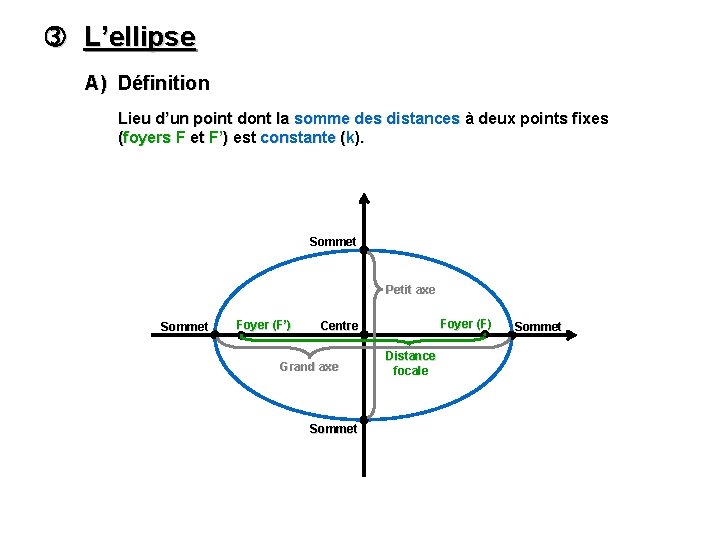
L’ellipse A) Définition Lieu d’un point dont la somme des distances à deux points fixes (foyers F et F’) est constante (k). Sommet Petit axe Sommet Foyer (F’) Foyer (F) Centre Grand axe Sommet Distance focale Sommet
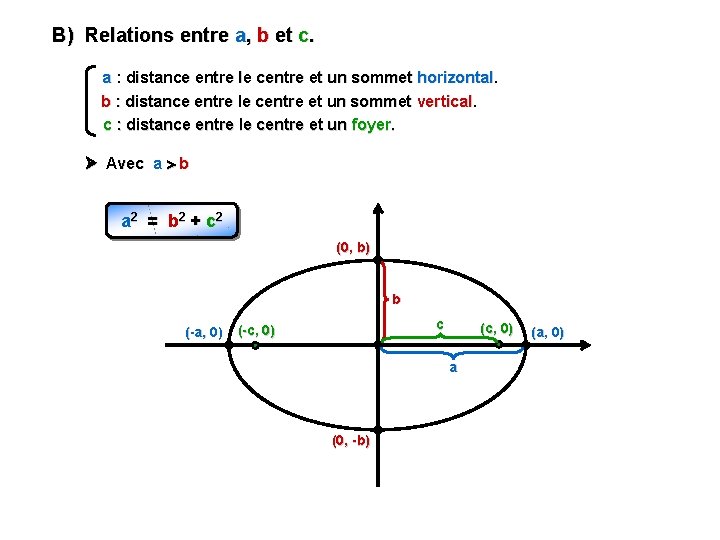
B) Relations entre a, b et c. a : distance entre le centre et un sommet horizontal. b : distance entre le centre et un sommet vertical. c : distance entre le centre et un foyer. Avec a b a 2 = b 2 + c 2 (0, b) b (-a, 0) c (-c, 0) (c, 0) a (0, -b) (a, 0)
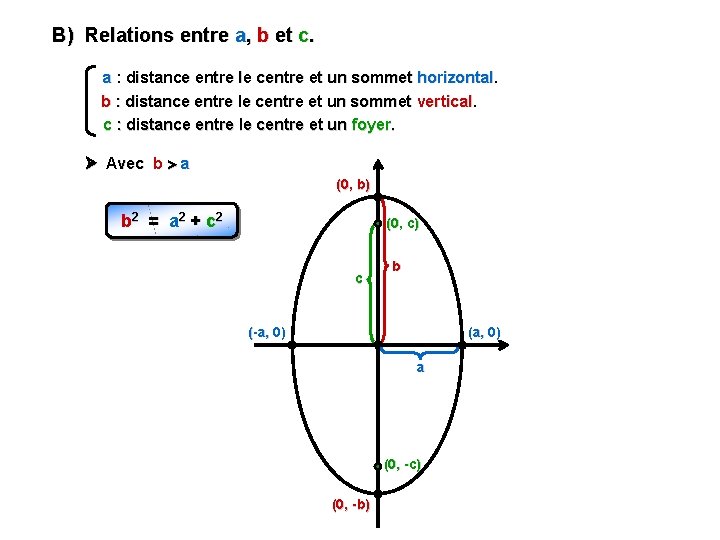
B) Relations entre a, b et c. a : distance entre le centre et un sommet horizontal. b : distance entre le centre et un sommet vertical. c : distance entre le centre et un foyer. Avec b a (0, b) b 2 = a 2 + c 2 (0, c) c b (a, 0) (-a, 0) a (0, -c) (0, -b)
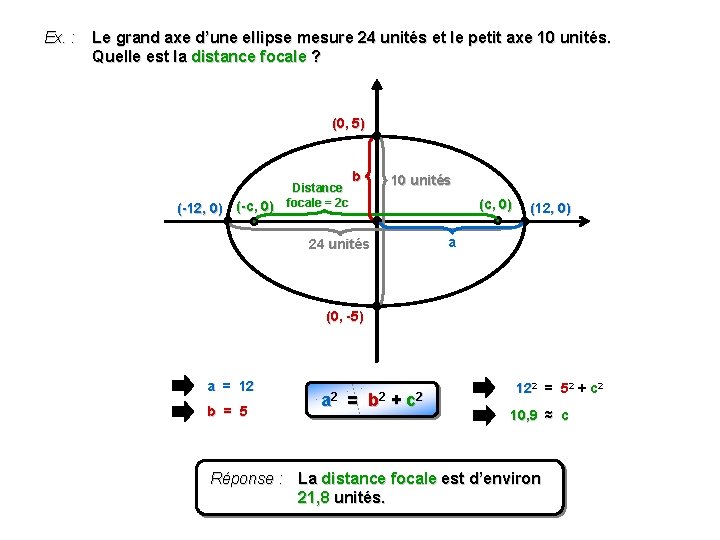
Ex. : Le grand axe d’une ellipse mesure 24 unités et le petit axe 10 unités. Quelle est la distance focale ? (0, 5) (-12, 0) (-c, 0) Distance focale = 2 c b 10 unités (c, 0) (12, 0) a 24 unités (0, -5) a = 12 b = 5 a 2 = b 2 + c 2 122 = 52 + c 2 10, 9 ≈ c Réponse : La distance focale est d’environ 21, 8 unités.
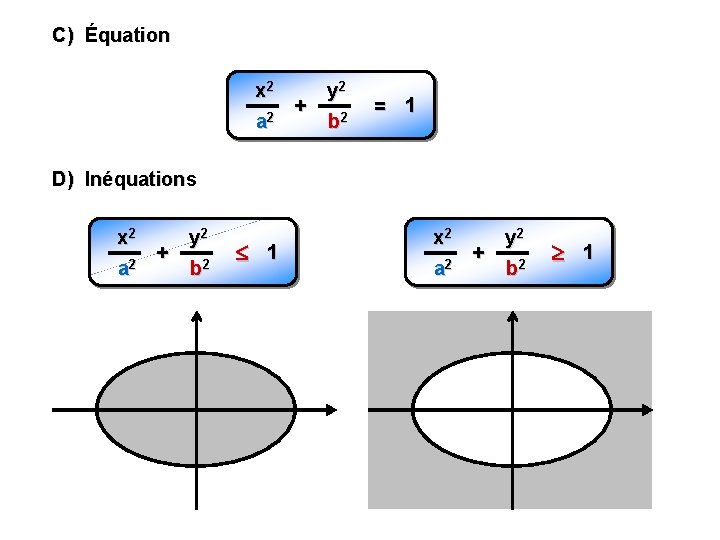
C) Équation x 2 + 2 a y 2 b 2 = 1 D) Inéquations x 2 + a 2 y 2 b 2 1
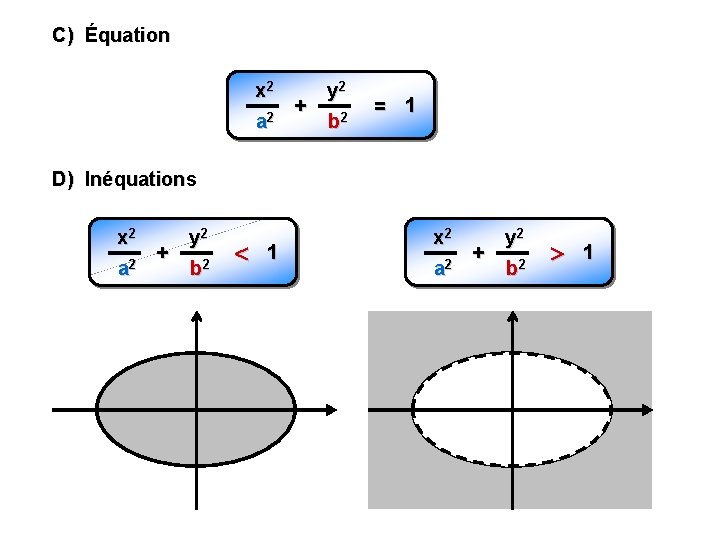
C) Équation x 2 + 2 a y 2 b 2 = 1 D) Inéquations x 2 + a 2 y 2 b 2 1
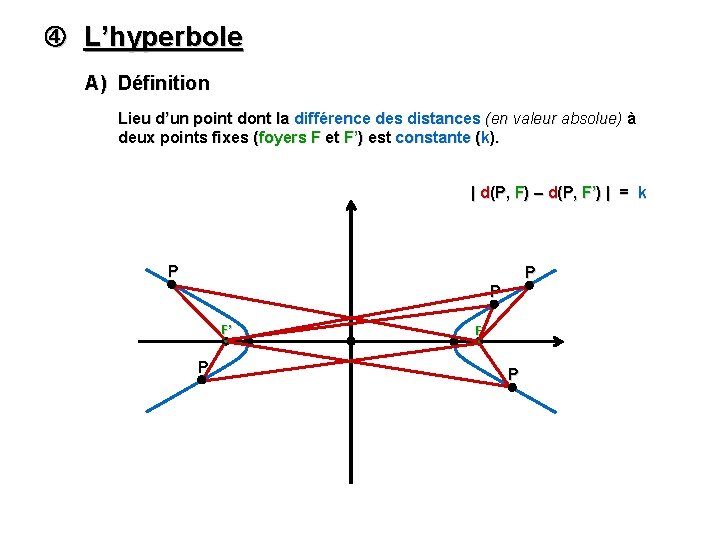
L’hyperbole A) Définition Lieu d’un point dont la différence des distances (en valeur absolue) à deux points fixes (foyers F et F’) est constante (k). | d(P, F) – d(P, F’) | = k P P P F’ P F P
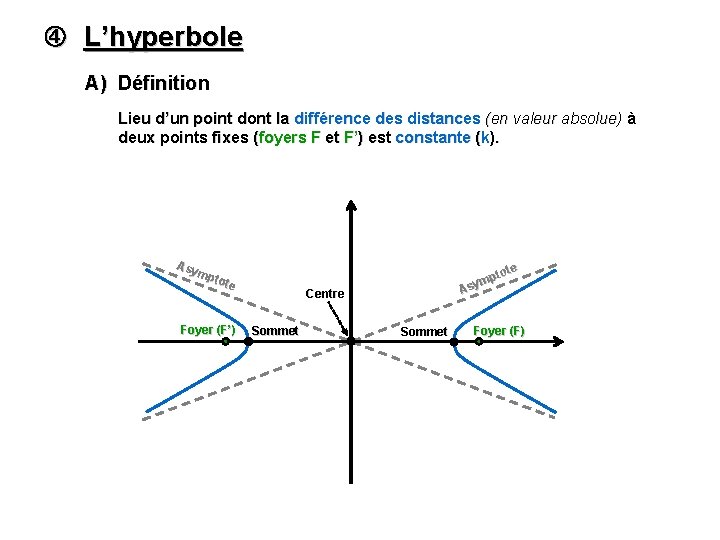
L’hyperbole A) Définition Lieu d’un point dont la différence des distances (en valeur absolue) à deux points fixes (foyers F et F’) est constante (k). Asy mp tote Foyer (F’) te pto m Asy Centre Sommet Foyer (F)
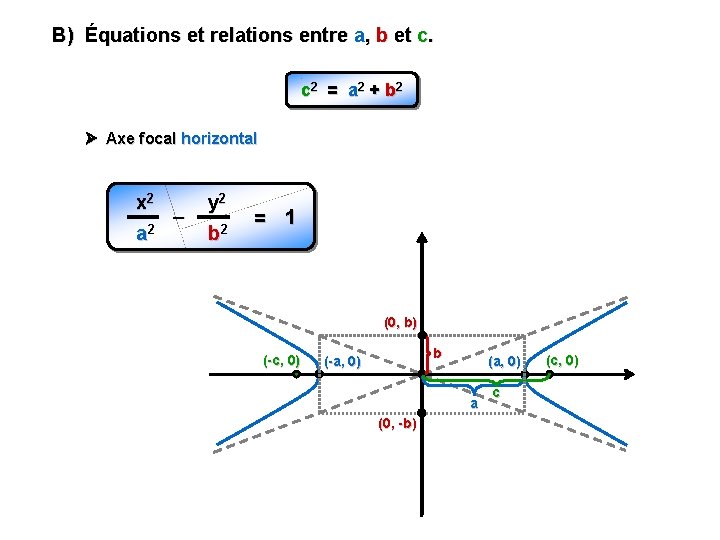
B) Équations et relations entre a, b et c. c 2 = a 2 + b 2 Axe focal horizontal x 2 – 2 a y 2 b 2 = 1 (0, b) (-c, 0) b (-a, 0) (a, 0) a (0, -b) c (c, 0)
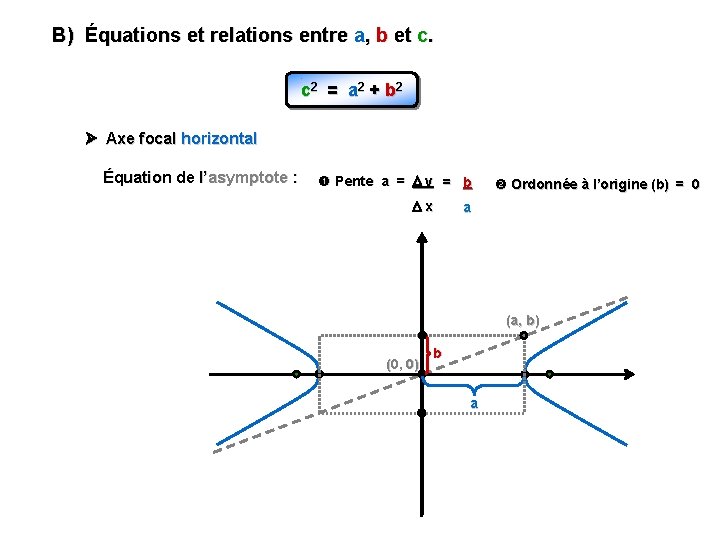
B) Équations et relations entre a, b et c. c 2 = a 2 + b 2 Axe focal horizontal Équation de l’asymptote : Pente a = y = b x Ordonnée à l’origine (b) = 0 a (a, b) (0, 0) b a
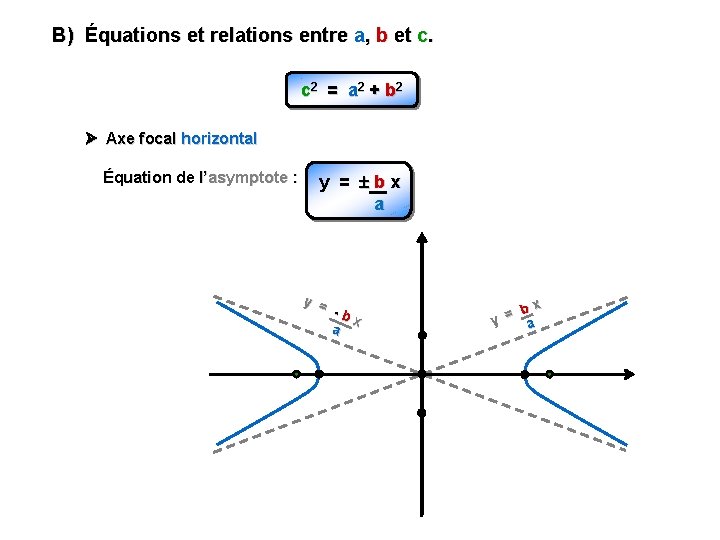
B) Équations et relations entre a, b et c. c 2 = a 2 + b 2 Axe focal horizontal Équation de l’asymptote : y = bx a y = -b x a bx = y a
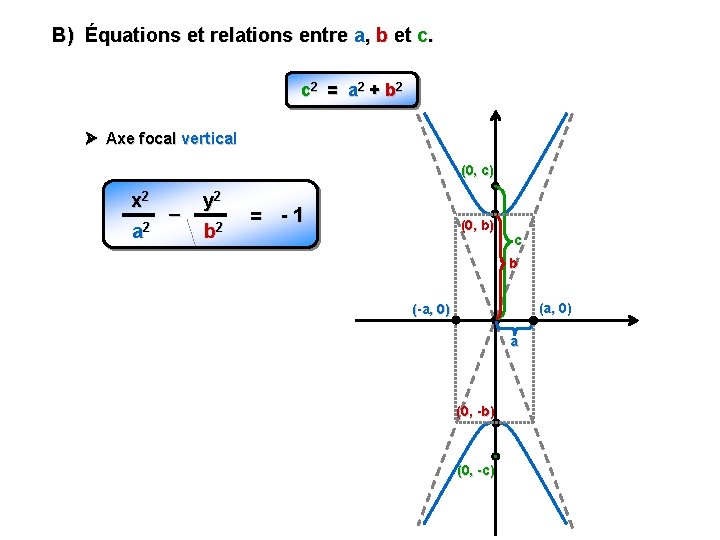
B) Équations et relations entre a, b et c. c 2 = a 2 + b 2 Axe focal vertical (0, c) x 2 – 2 a y 2 b 2 = -1 (0, b) c b (a, 0) (-a, 0) a (0, -b) (0, -c)
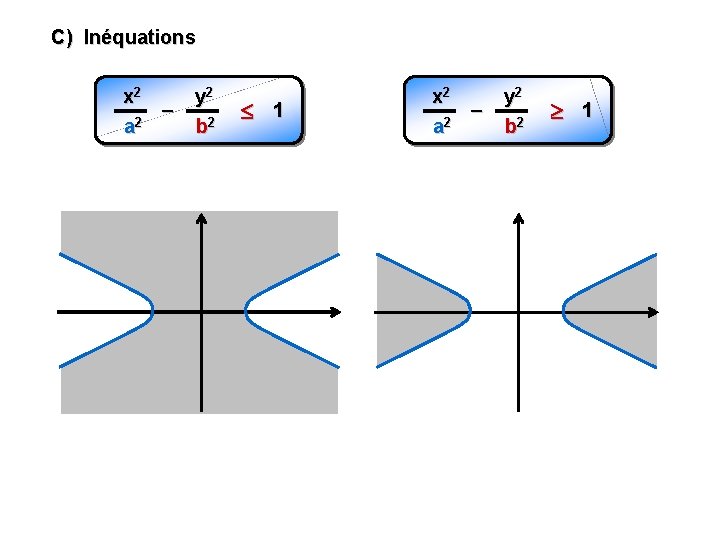
C) Inéquations x 2 – 2 a y 2 b 2 1
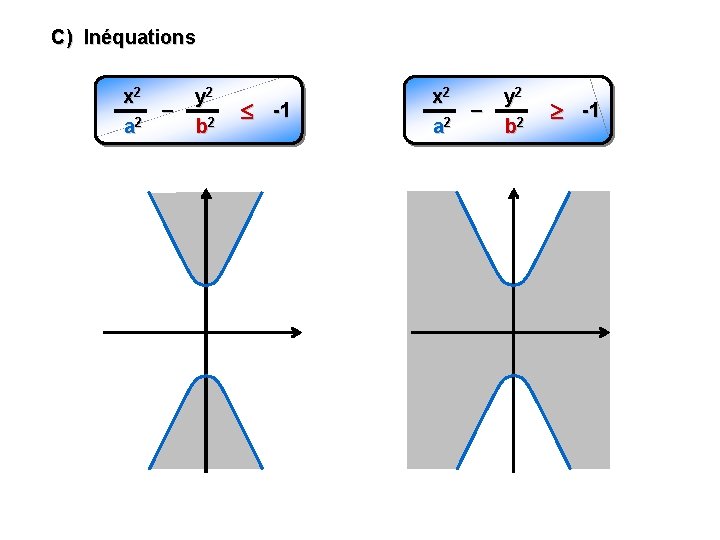
C) Inéquations x 2 – 2 a y 2 b 2 -1
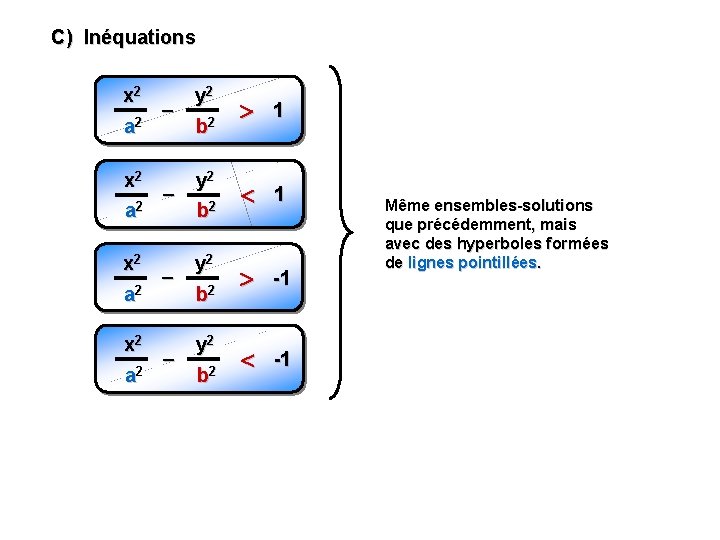
C) Inéquations x 2 – 2 a y 2 b 2 1 x 2 – 2 a y 2 b 2 -1 Même ensembles-solutions que précédemment, mais avec des hyperboles formées de lignes pointillées.
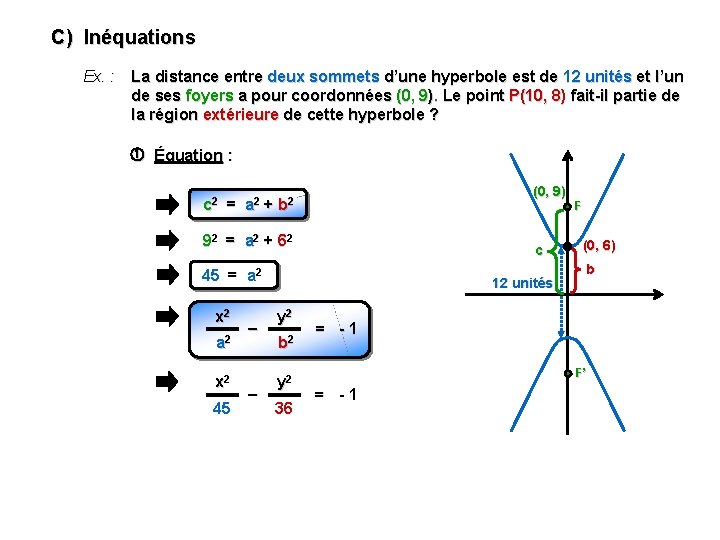
C) Inéquations Ex. : La distance entre deux sommets d’une hyperbole est de 12 unités et l’un de ses foyers a pour coordonnées (0, 9). Le point P(10, 8) fait-il partie de la région extérieure de cette hyperbole ? Équation : (0, 9) c 2 = a 2 + b 2 92 = a 2 + 62 c 45 = a 2 x 2 45 – – 12 unités y 2 b 2 y 2 36 F (0, 6) b = -1 F’ = -1
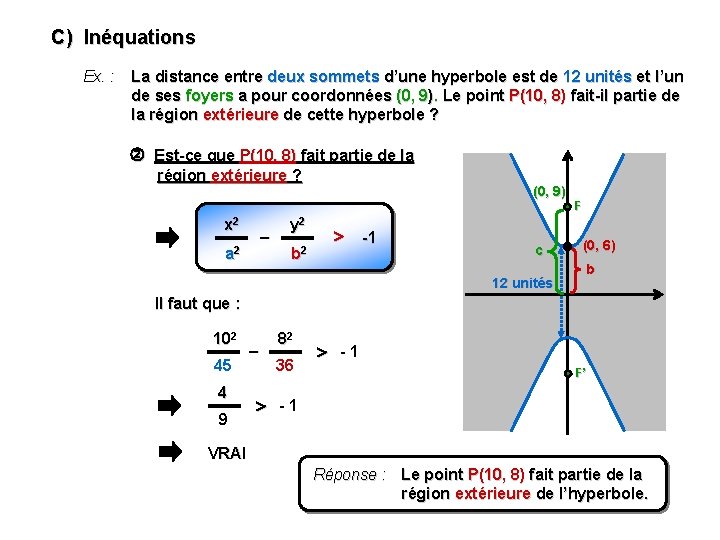
C) Inéquations Ex. : La distance entre deux sommets d’une hyperbole est de 12 unités et l’un de ses foyers a pour coordonnées (0, 9). Le point P(10, 8) fait-il partie de la région extérieure de cette hyperbole ? Est-ce que P(10, 8) fait partie de la région extérieure ? x 2 – a 2 y 2 b 2 (0, 9) -1 c 12 unités F (0, 6) b Il faut que : 102 45 4 9 – 82 36 -1 F’ -1 VRAI Réponse : Le point P(10, 8) fait partie de la région extérieure de l’hyperbole.
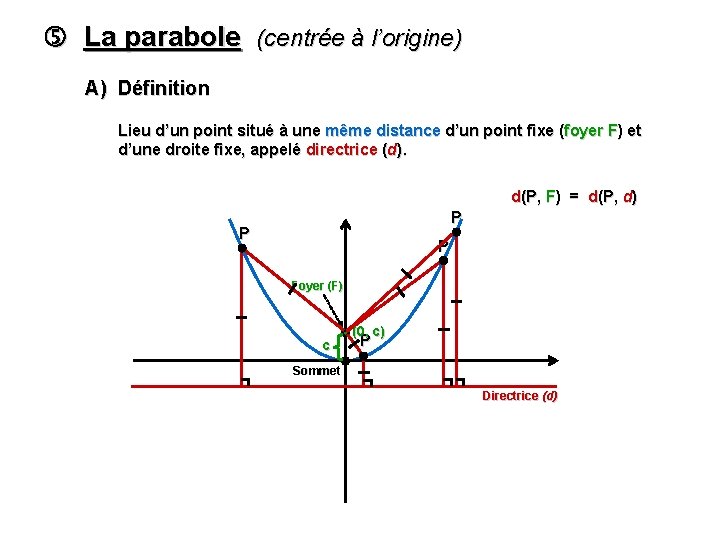
La parabole (centrée à l’origine) A) Définition Lieu d’un point situé à une même distance d’un point fixe (foyer F) et d’une droite fixe, appelé directrice (d). d(P, F) = d(P, d) P P P Foyer (F) c (0, c) P Sommet Directrice (d)
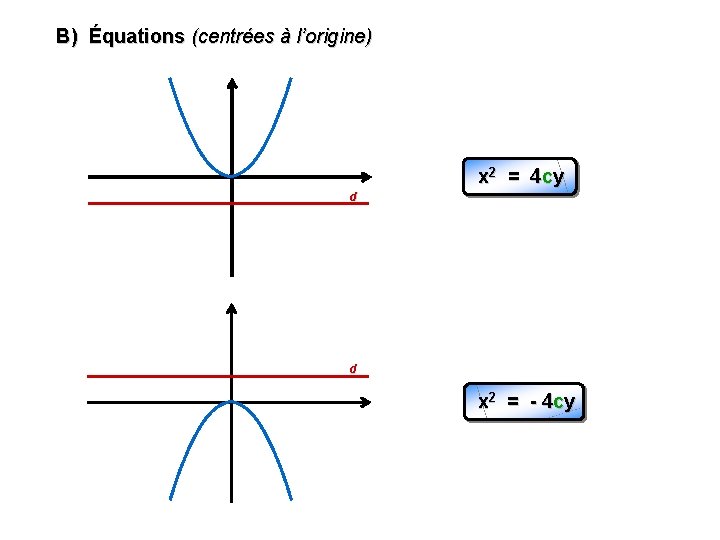
B) Équations (centrées à l’origine) x 2 = 4 cy d d x 2 = - 4 cy
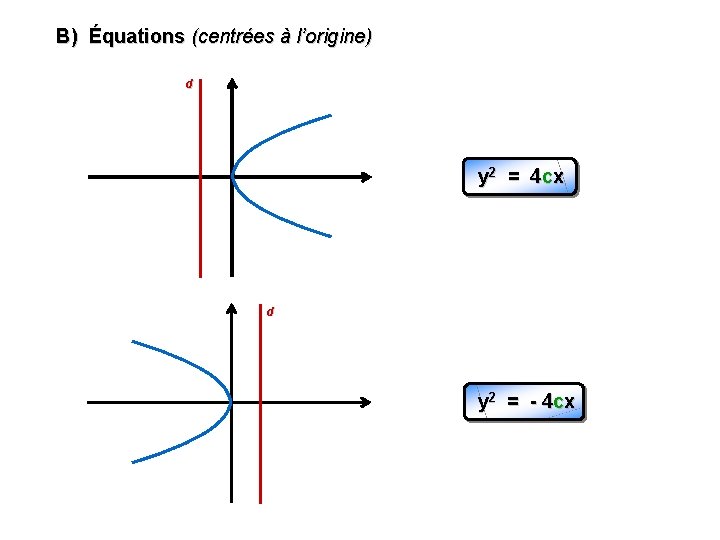
B) Équations (centrées à l’origine) d y 2 = 4 cx d y 2 = - 4 cx

B) Équations (centrées à l’origine) Ex. : Une parabole centrée à l’origine a pour foyer le point F(0, -6). Cette parabole passe-t-elle par le point P(-12, -6) ? d Réponse : La parabole passe par le point P(-12, -6). c (0, -6) Équation : Est-ce que la parabole passe par le point P(-12, -6) ? x 2 = - 4 cy (-12)2 = - 24(-6) x 2 = - 4(6)y 144 = 144 x 2 = - 24 y VRAI
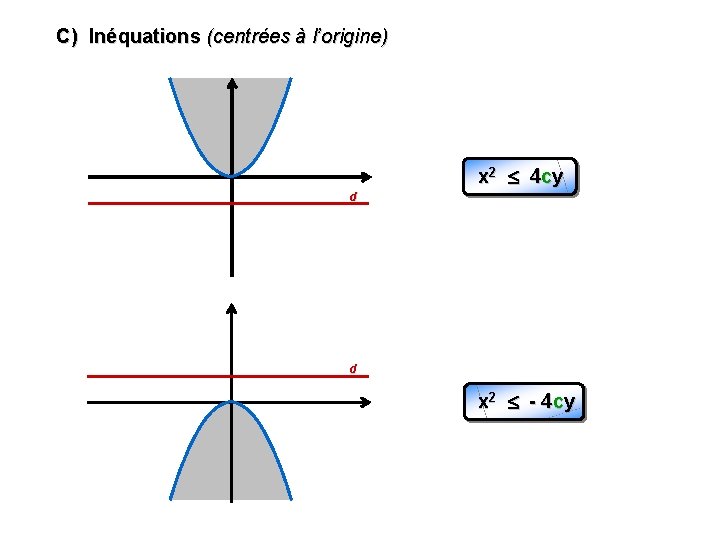
C) Inéquations (centrées à l’origine) x 2 4 cy d d x 2 - 4 cy
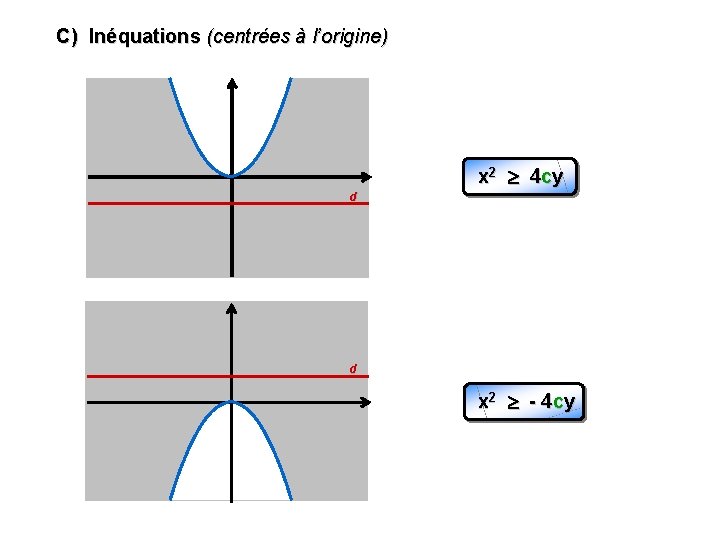
C) Inéquations (centrées à l’origine) x 2 4 cy d d x 2 - 4 cy
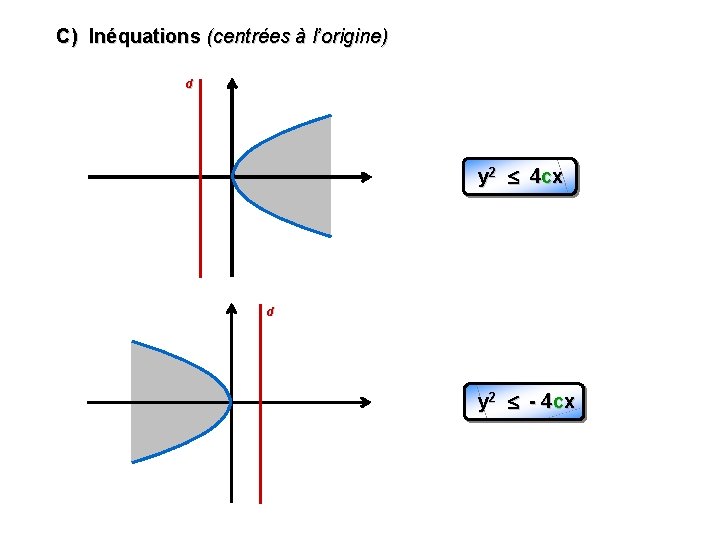
C) Inéquations (centrées à l’origine) d y 2 4 cx d y 2 - 4 cx
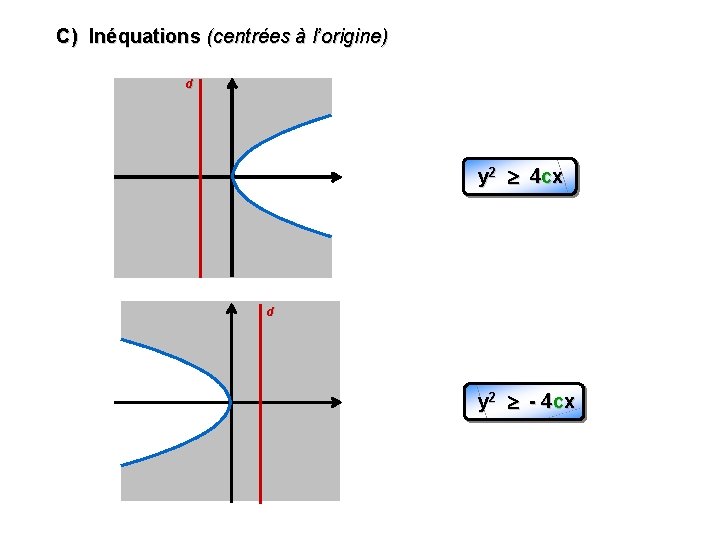
C) Inéquations (centrées à l’origine) d y 2 4 cx d y 2 - 4 cx
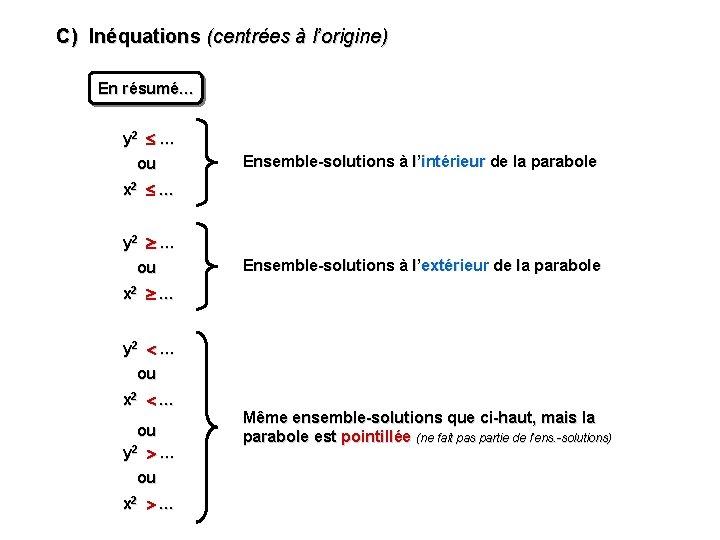
C) Inéquations (centrées à l’origine) En résumé… y 2 … ou Ensemble-solutions à l’intérieur de la parabole x 2 … y 2 … ou Ensemble-solutions à l’extérieur de la parabole x 2 … y 2 … ou x 2 … ou y 2 … ou x 2 … Même ensemble-solutions que ci-haut, mais la parabole est pointillée (ne fait pas partie de l’ens. -solutions)
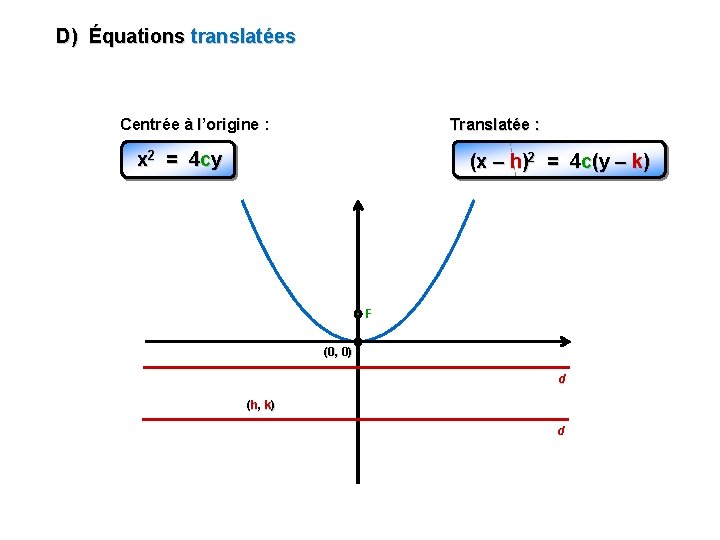
D) Équations translatées Centrée à l’origine : Translatée : x 2 = 4 cy (x – h)2 = 4 c(y – k) F (0, 0) d (h, k) d
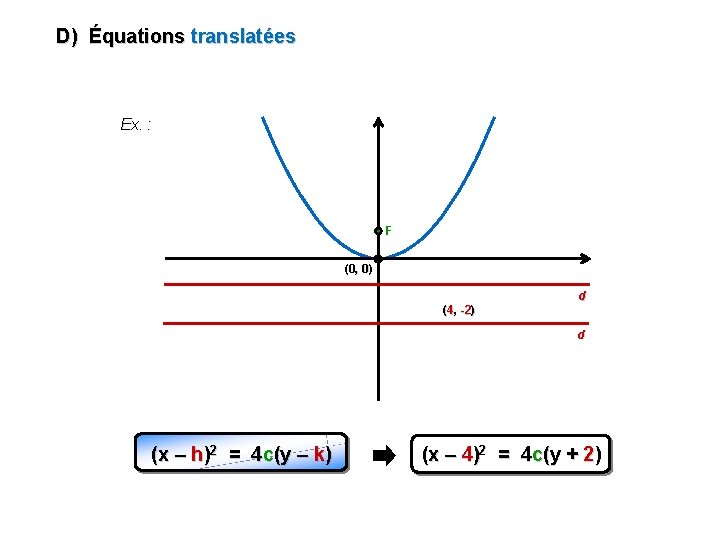
D) Équations translatées Ex. : F (0, 0) d (4, -2) d (x – h)2 = 4 c(y – k) (x – 4)2 = 4 c(y + 2)
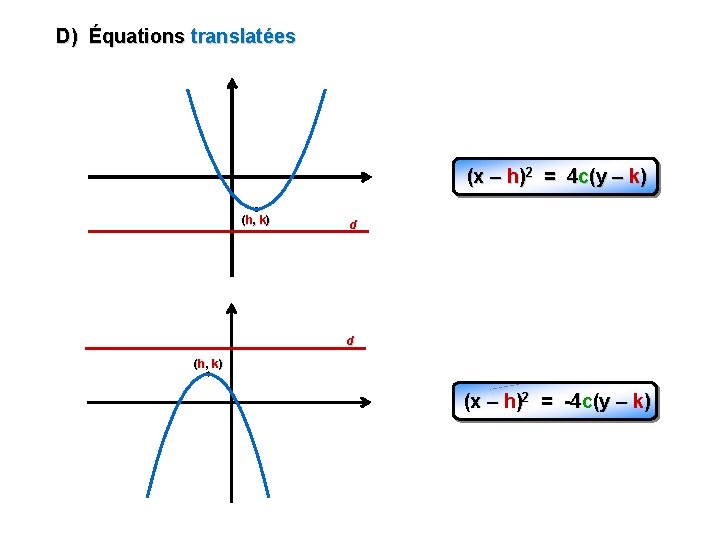
D) Équations translatées (x – h)2 = 4 c(y – k) (h, k) d d (h, k) (x – h)2 = -4 c(y – k)
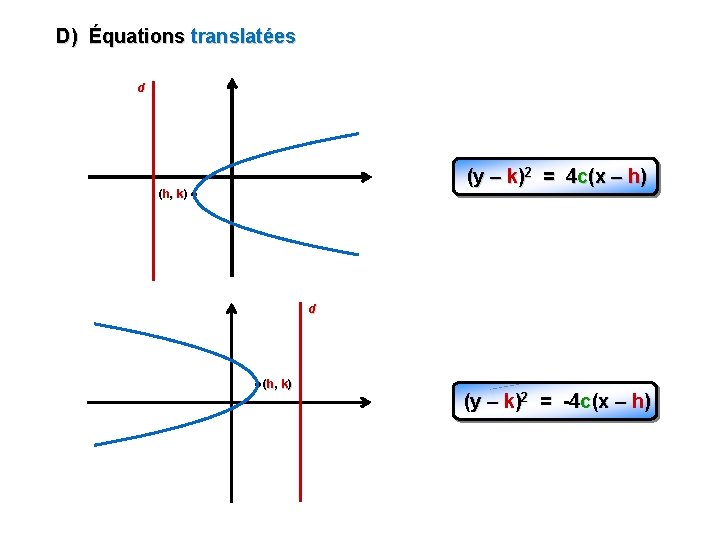
D) Équations translatées d (y – k)2 = 4 c(x – h) (h, k) d (h, k) (y – k)2 = -4 c(x – h)
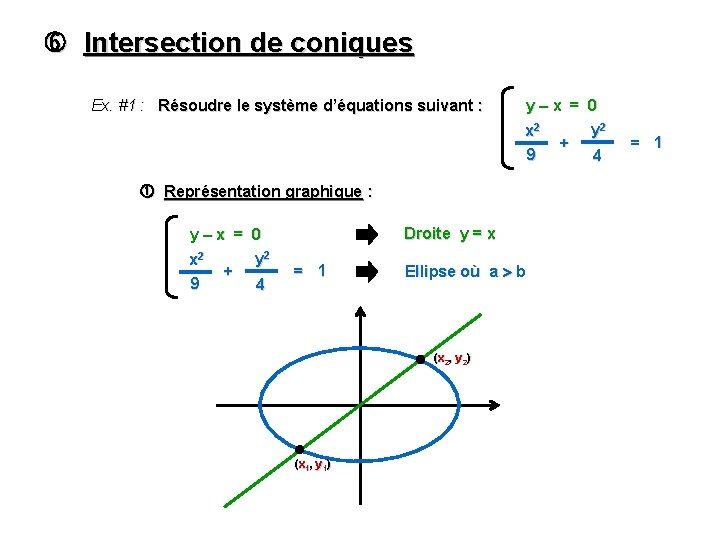
Intersection de coniques Ex. #1 : Résoudre le système d’équations suivant : y–x = 0 y 2 x 2 + 9 4 Représentation graphique : y–x = 0 y 2 x 2 + 9 4 Droite y = x = 1 Ellipse où a b (x 2, y 2) (x 1, y 1) = 1
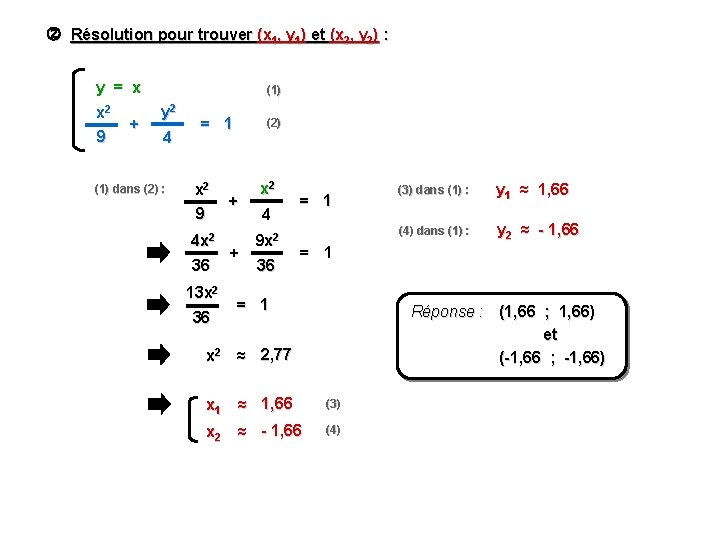
Résolution pour trouver (x 1, y 1) et (x 2, y 2) : y = x x 2 9 + (1) y 2 4 (1) dans (2) : = 1 x 2 9 (2) + 4 x 2 + 36 13 x 2 36 x 2 4 9 x 2 36 = 1 (3) dans (1) : y 1 ≈ 1, 66 (4) dans (1) : y 2 ≈ - 1, 66 = 1 Réponse : (1, 66 ; 1, 66) et (-1, 66 ; -1, 66) x 2 ≈ 2, 77 x 1 ≈ 1, 66 (3) x 2 ≈ - 1, 66 (4)
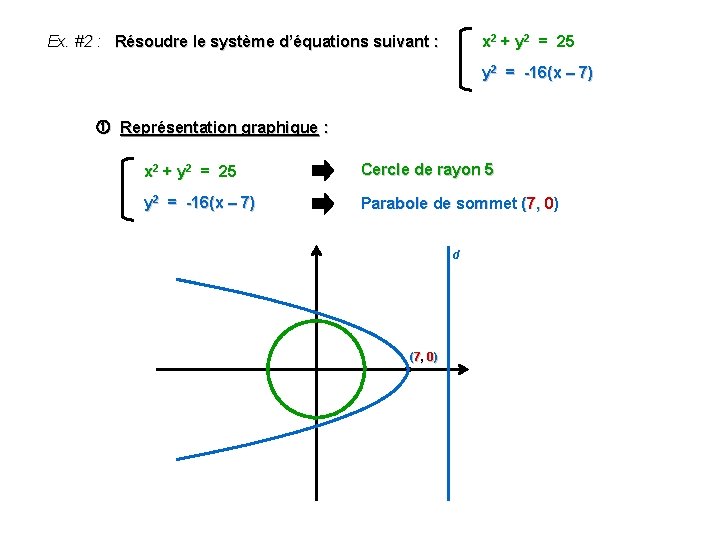
Ex. #2 : Résoudre le système d’équations suivant : x 2 + y 2 = 25 y 2 = -16(x – 7) Représentation graphique : x 2 + y 2 = 25 Cercle de rayon 5 y 2 = -16(x – 7) Parabole de sommet (7, 0) d (7, 0)

Résolution pour trouver (x 1, y 1) et (x 2, y 2) : x 2 + y 2 = 25 (1) y 2 = -16(x – 7) (2) dans (1) : x 2 + -16(x – 7) = 25 x 2 – 16 x + 112 = 25 x 2 -16 x + 87 = 0 x Réponse : Il n'y a aucun solution.
- Slides: 45