Les automates programmables 1 6 Les oprateurs logiques

Les automates programmables « 1. 6. Les opérateurs logiques » A T Training On Line

Séquence 1 animation 6 – Les opérateurs logiques – Fonction OUI Les équations logiques sont composées de fonctions élémentaires. Chacune de ces fonctions assure une opération, ce qui fait qu’on les appelle aussi des opérateurs logiques. 1 - Fonction OUI Cette fonction n’est pas utilisée en tant que fonction. a 0 1 A T Training On Line s 0 1 S=a La sortie S est égale à 1 si la variable a est à 1. 2

Séquence 1 animation 6 – Les opérateurs logiques – Fonction NON 2 - Fonction NON, ou complément (NO) L’opérateur NON inverse le signal d’entrée, on dit qu’il le complémente. a 0 1 A T Training On Line s 1 0 S=a La sortie est à l’état 1 si l’entrée est à l’état 0 et inversement. 3

Séquence 1 animation 6 – Les opérateurs logiques – Fonction ET 3 - Fonction ET, ou produit logique (AND) a 0 0 1 b 0 1 0 s 0 0 0 1 1 1 S = a. b (S = a ET b) La sortie est à l’état 1 si toutes les entrées sont à l’état 1. a b s Si un opérateur ET possède n entrées, il faut que ces n entrées soient à l’état 1 pour que la sortie soit à l’état 1, ce qui oblige à mettre au 1 logique les entrées non utilisées. A T Training On Line 4

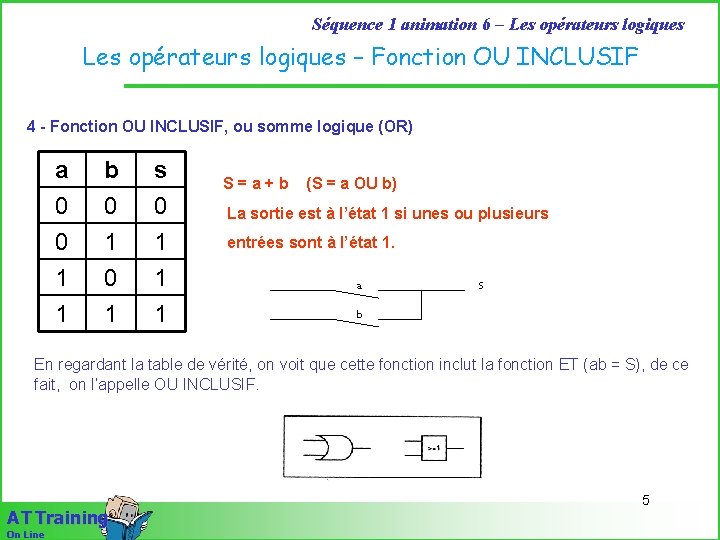
Séquence 1 animation 6 – Les opérateurs logiques – Fonction OU INCLUSIF 4 - Fonction OU INCLUSIF, ou somme logique (OR) a 0 0 1 b 0 1 0 s 0 1 1 1 S=a+b (S = a OU b) La sortie est à l’état 1 si unes ou plusieurs entrées sont à l’état 1. a S b En regardant la table de vérité, on voit que cette fonction inclut la fonction ET (ab = S), de ce fait, on l’appelle OU INCLUSIF. A T Training On Line 5

Séquence 1 animation 6 – Les opérateurs logiques – Fonction OU EXCLUSIF 5 - Fonction OU EXCLUSIF (XOR – OUX – EXOR) a 0 0 1 b 0 1 0 s 0 1 1 0 A T Training On Line S=a b ( S = a OU exclusif b) La sortie est à l’état 1 si une ou l'autre, mais une et une seule des entrées est à l’état 1. 6

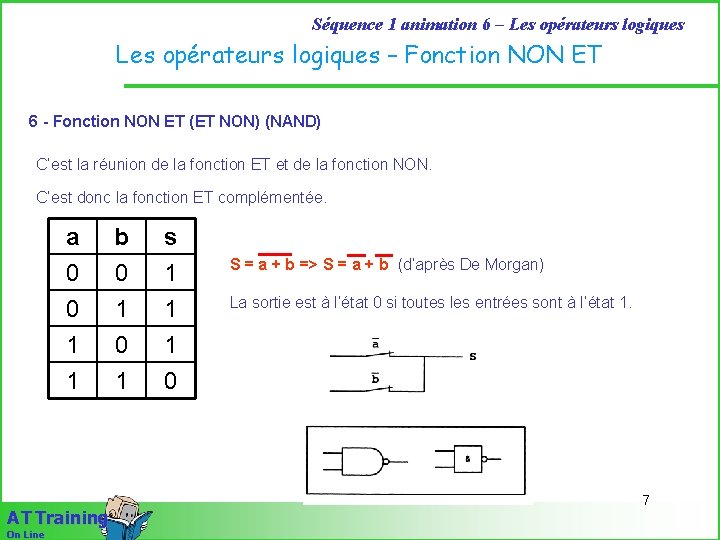
Séquence 1 animation 6 – Les opérateurs logiques – Fonction NON ET 6 - Fonction NON ET (ET NON) (NAND) C’est la réunion de la fonction ET et de la fonction NON. C’est donc la fonction ET complémentée. a 0 0 1 b 0 1 0 s 1 1 1 0 A T Training On Line S = a + b => S = a + b (d’après De Morgan) La sortie est à l’état 0 si toutes les entrées sont à l’état 1. 7

Séquence 1 animation 6 – Les opérateurs logiques – Fonction NON OU 7 - Fonction NON OU (OU NON) (NOR) C’est la réunion de la fonction OU et de la fonction NON. C’est donc la fonction OU complémentée. a b s 0 0 1 0 1 0 0 1 1 0 A T Training On Line S = a + b => S = ab (d’après De Morgan) La sortie est à l’état 0 si une ou plusieurs entrées sont à l’état 1. 8

Séquence 1 animation 6 – Les opérateurs logiques Relations fondamentales d’algèbre de Boole PROPRIETES PRODUIT ADDITION Indempotence a. a = a a+a = a Commutativité a. b = b. a a+b = b+a Associativité a. (b. c) = (a. b). c + a + (b+c) = (a+b) + c Absorption a. (a. b) = a. b a + a. b = a Distributivité a. (b+c) = a. b + a. c a + b. c = (a+b) (a+c) Complémentarité _ a. a = 0 _ a + a = 1 Involution A T Training On Line = a = a 9

Séquence 1 animation 6 – Les opérateurs logiques De Morgan - Théorème Augustus De Morgan, mathématicien et logicien anglais (1806 – 1871). Le complément d’une somme booléenne est égal au produit booléen des compléments de chaque facteur de la somme. ____ _ _ a+b =a. b Le complément d’un produit booléen est égal à la somme booléenne des compléments de chaque facteur du produit. ____ _ _ a. b =a+b Les relations fondamentales ainsi que le théorème de De Morgan sont très utilisées pour : - simplifier des équations logiques, - pour l’écriture de certains programmes quand les fonctions logiques de base ne sont pas toutes implémentées dans le langage de l’automate ou de l’ordinateur utilisé. A T Training On Line 10