LES ANGLES 1 Dfinitions Exercice 1 Exercice 2

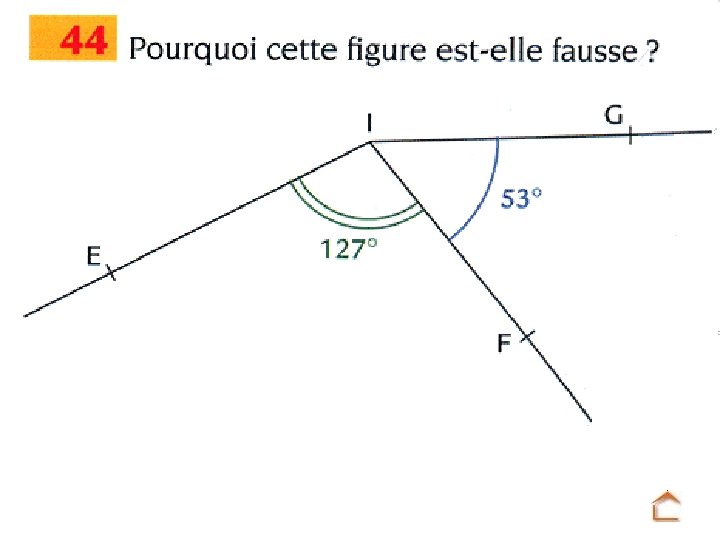
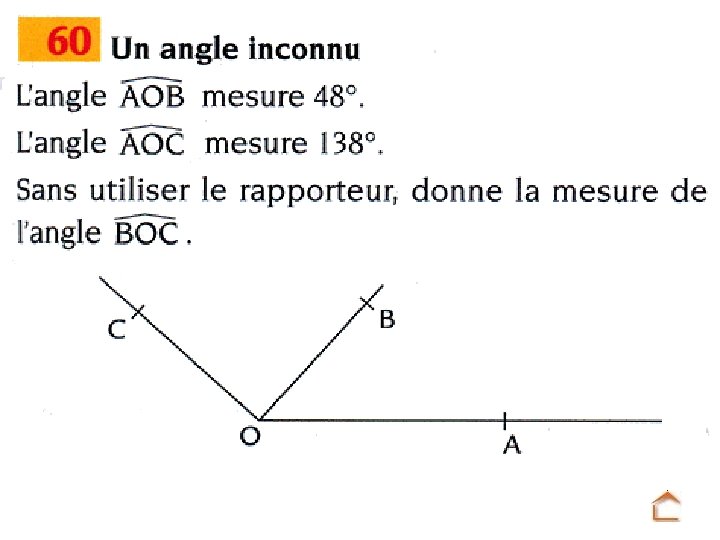
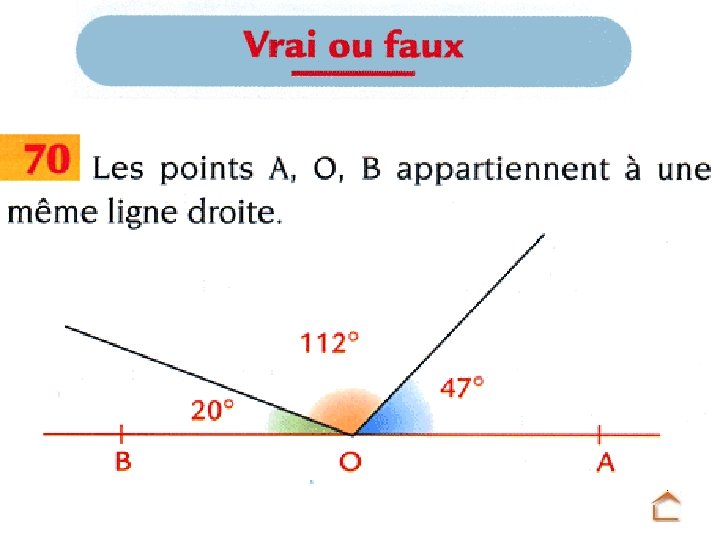
LES ANGLES 1. Définitions Exercice 1 Exercice 2 2. Angles particuliers 3. Angle aigu, angle obtus 4. Mesure des angles Exercice 3 42 p. 148 5. Construction d’angles Ex. 5 17 p. 145 6. Reproduire un angle Ex 6 7. Bissectrice d’un angle 43 p. 149 44 p. 149 8. Propriété de la symétrie axiale 60 p. 151 70 p. 152 8 p. 240 10 p. 241

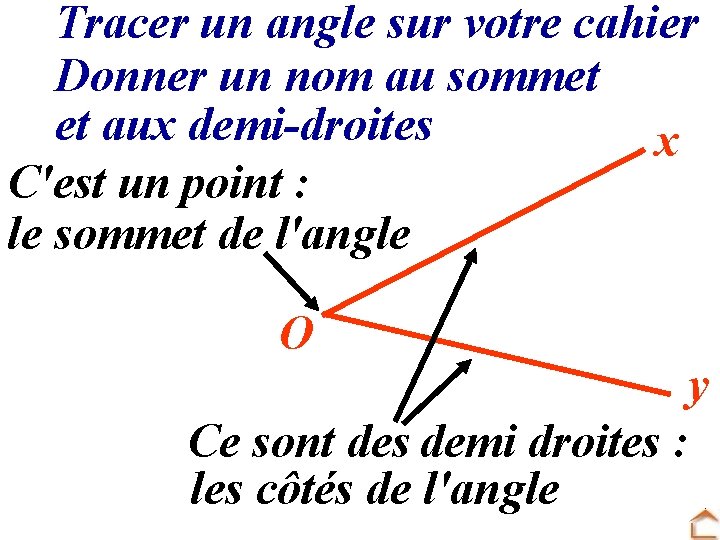
Tracer un angle sur votre cahier Donner un nom au sommet et aux demi-droites x C'est un point : le sommet de l'angle O y Ce sont des demi droites : les côtés de l'angle

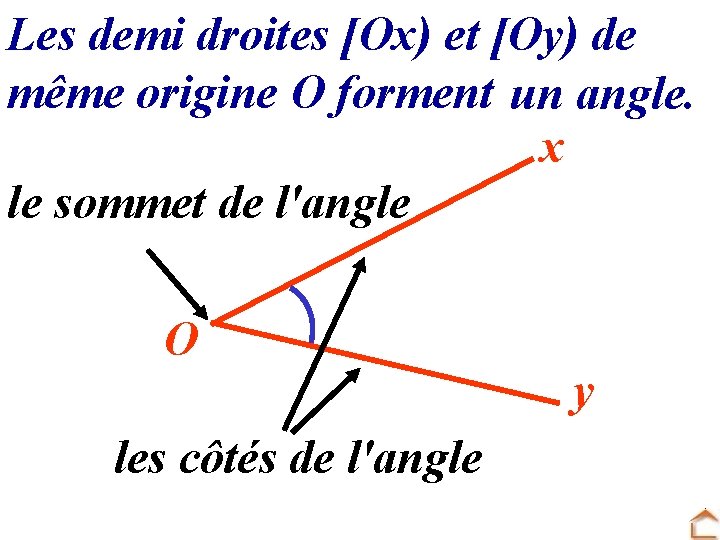
Les demi droites [Ox) et [Oy) de même origine O forment un angle. x le sommet de l'angle O les côtés de l'angle y

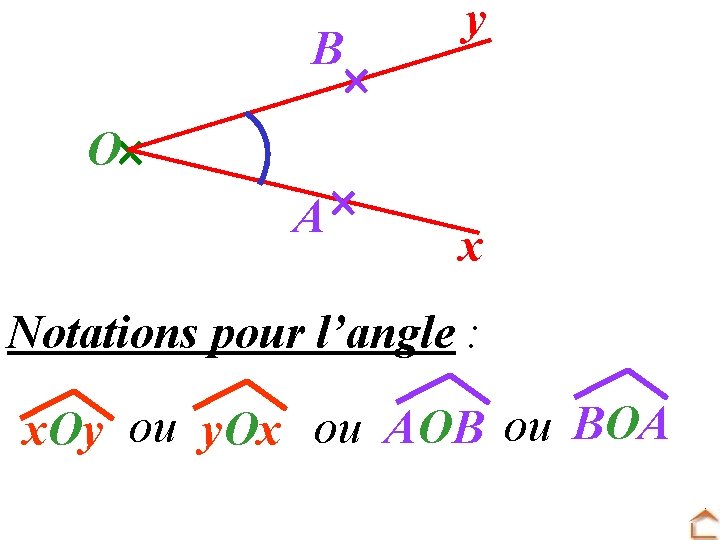
B O A y x Notations pour l’angle : x. Oy ou y. Ox ou AOB ou BOA

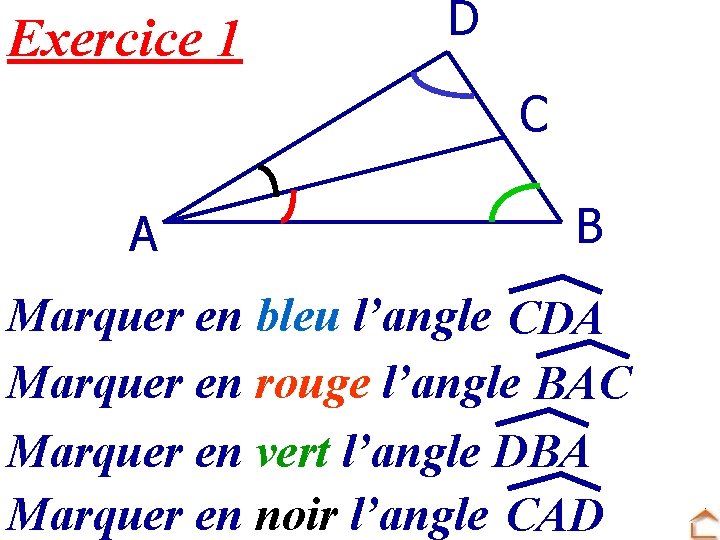
Exercice 1 D C A B Marquer en bleu l’angle CDA Marquer en rouge l’angle BAC Marquer en vert l’angle DBA Marquer en noir l’angle CAD

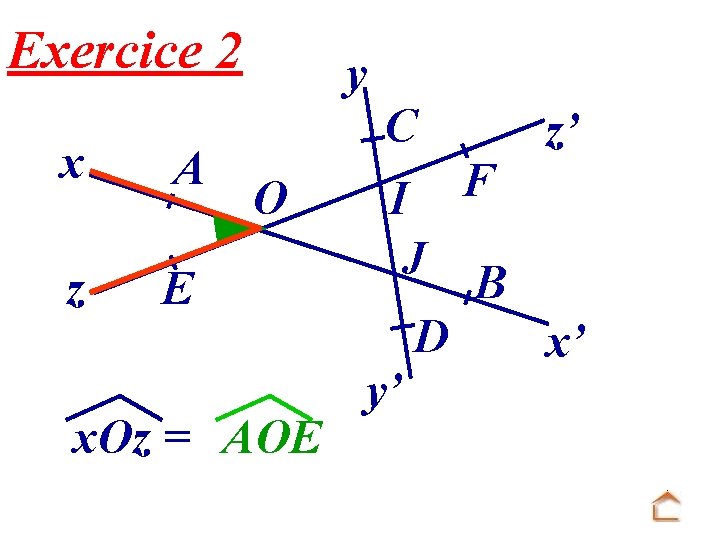
Exercice 2 x A z E y O x. Oz = AOE C I J D y’ F z’ B x’

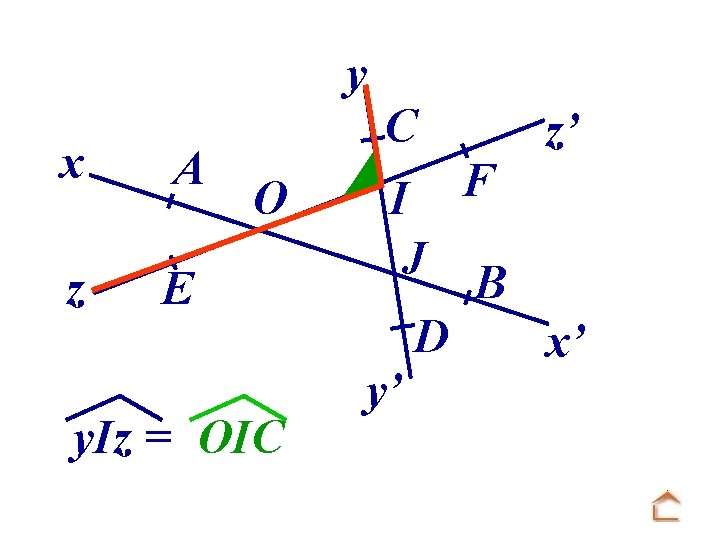
y x A z E O y. Iz = OIC C I J D y’ F z’ B x’

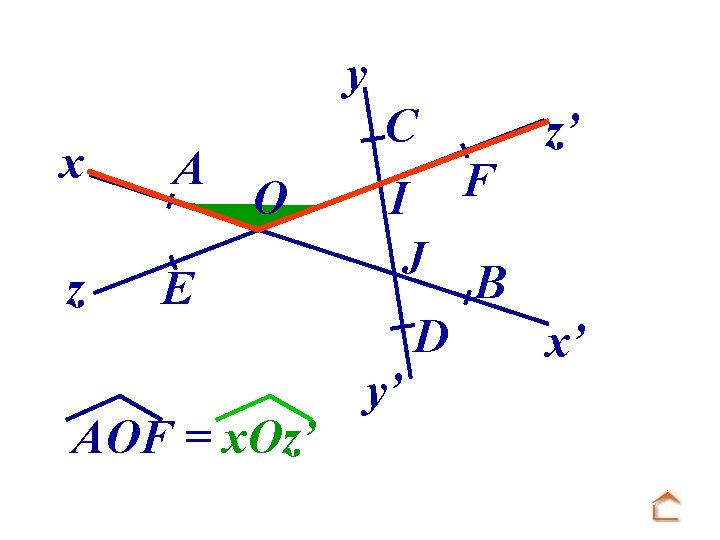
y x A z E O AOF = x. Oz’ C I J D y’ F z’ B x’

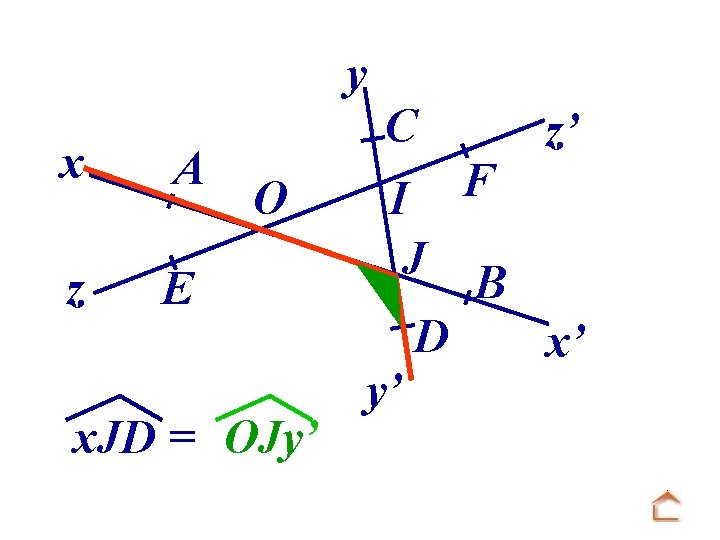
y x A z E O x. JD = OJy’ C I J D y’ F z’ B x’

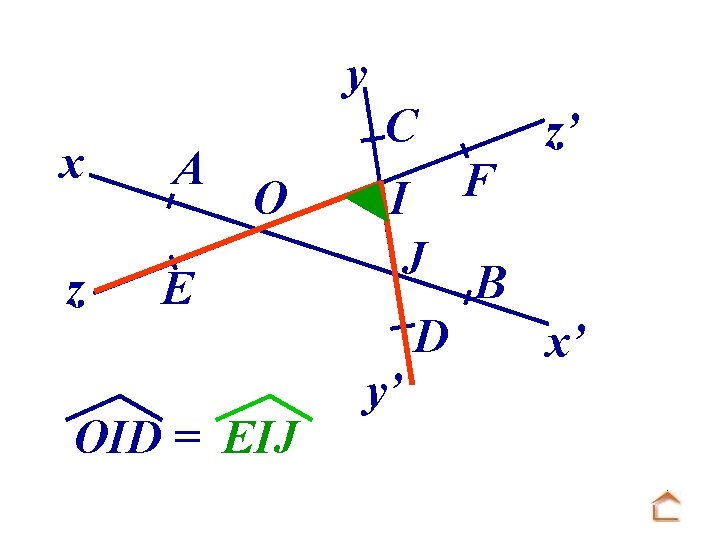
y x A z E O OID = EIJ C I J D y’ F z’ B x’

2. Angles particuliers O y x x. Oy est un angle nul.

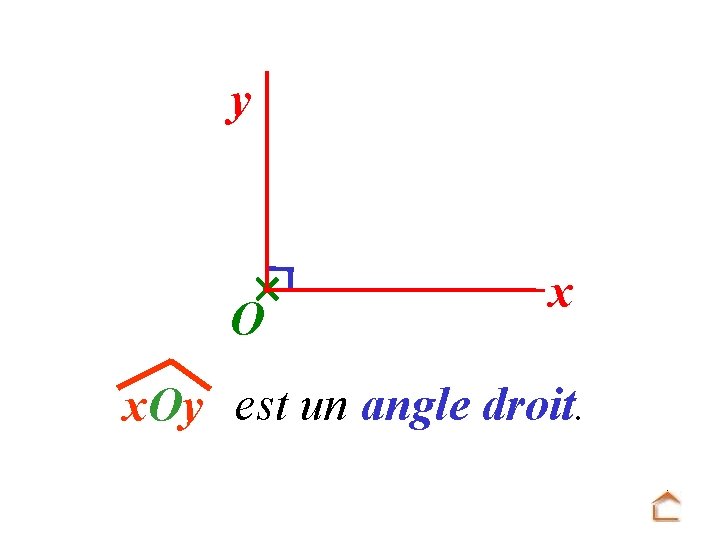
y O x x. Oy est un angle droit.

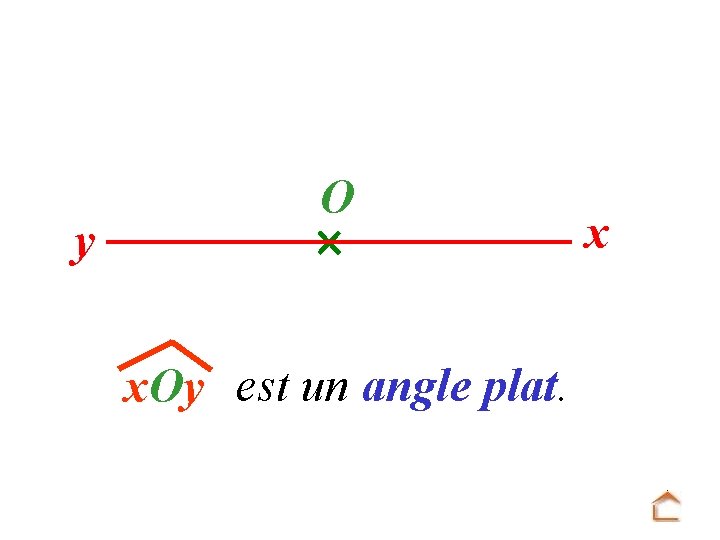
y O x. Oy est un angle plat. x

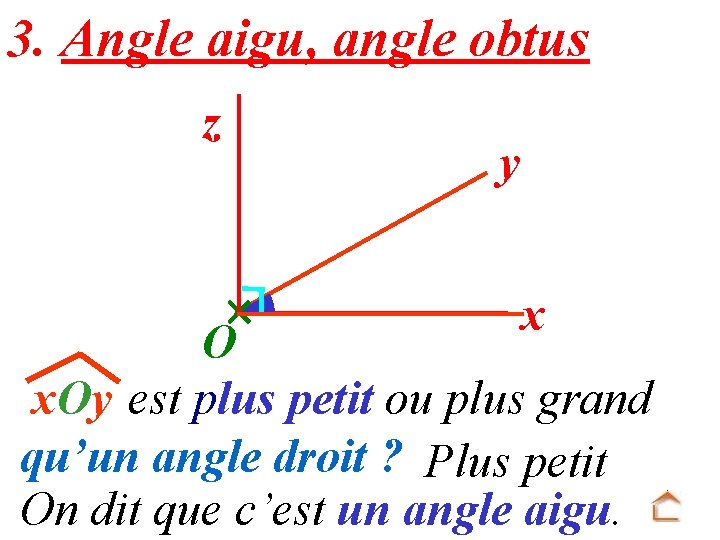
3. Angle aigu, angle obtus z y x O x. Oy est plus petit ou plus grand qu’un angle droit ? Plus petit On dit que c’est un angle aigu.

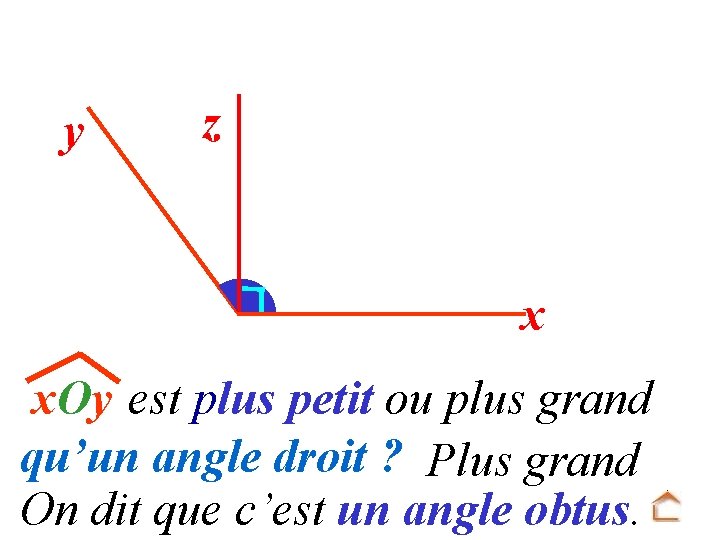
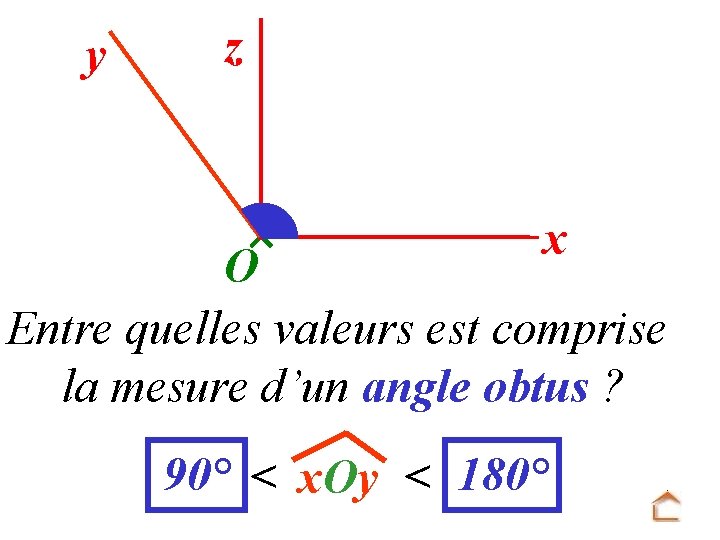
y z x x. Oy est plus petit ou plus grand qu’un angle droit ? Plus grand On dit que c’est un angle obtus.

4. Mesure des angles a) Cas particuliers b) Graduer un rapporteur c) Utilisation du rapporteur

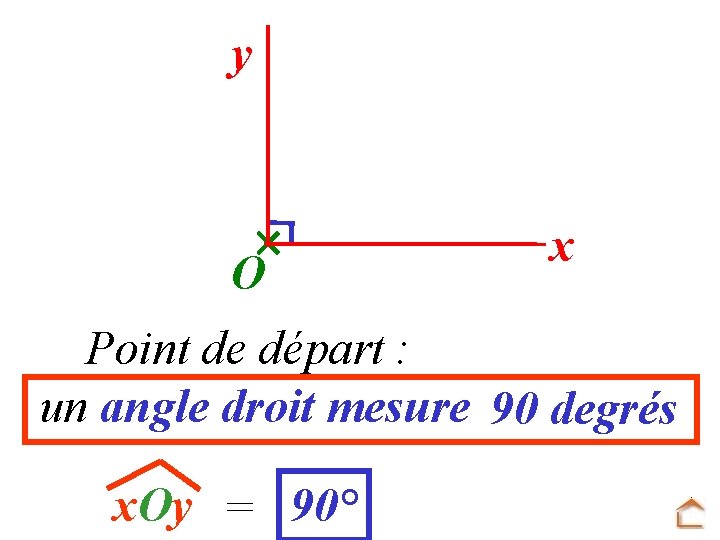
y O x Point de départ : un angle droit mesure 90 degrés x. Oy = 90°

y O x Combien mesure un angle plat ? x. Oy = 180°

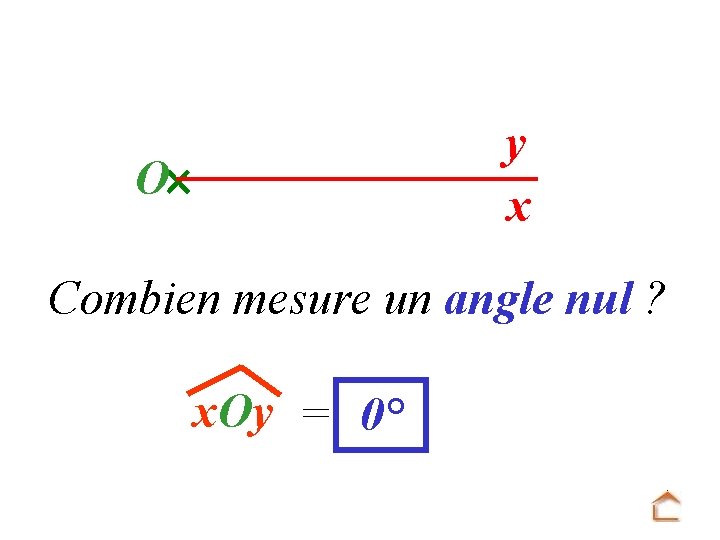
y x O Combien mesure un angle nul ? x. Oy = 0°

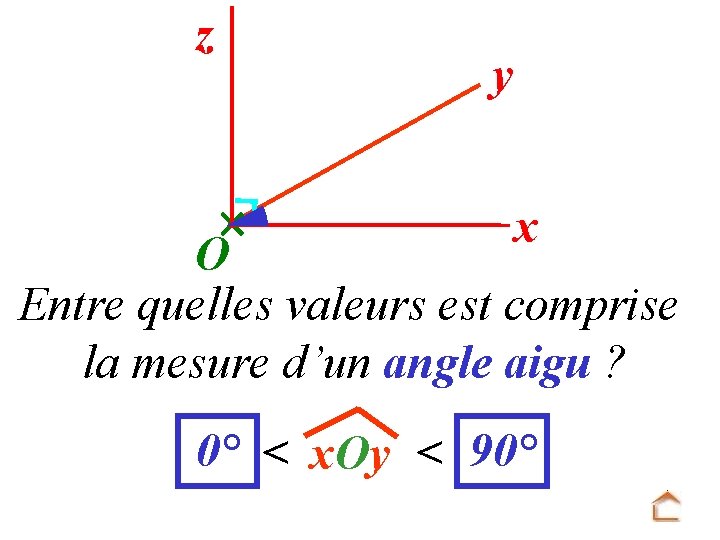
z y x O Entre quelles valeurs est comprise la mesure d’un angle aigu ? 0° < x. Oy < 90°

y z x O Entre quelles valeurs est comprise la mesure d’un angle obtus ? 90° < x. Oy < 180°

Un rapporteur non gradué va vous être distribué, à vous de trouver à combien de degrés correspond chaque graduation. Pour cela, coller le rapporteur sur le cahier et écrire les graduations au crayon de bois.

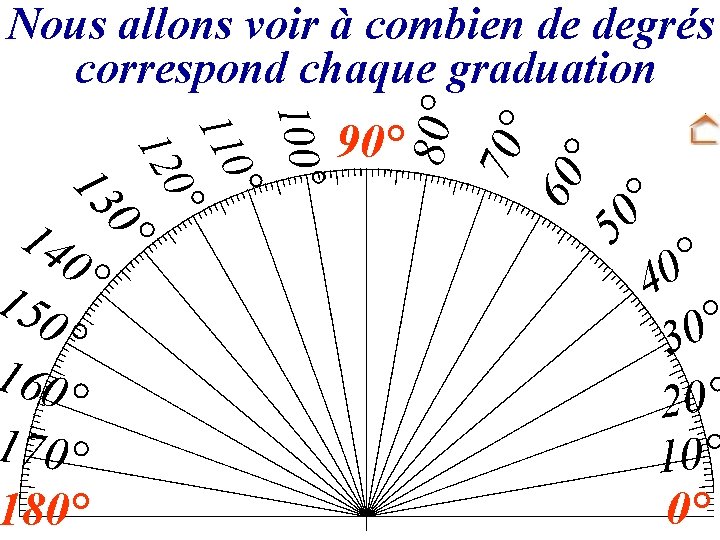
100° ° 110 0° 12 15 0° 13 14 0° 0° 160° 170° 180° 70° 60 ° 50 ° Nous allons voir à combien de degrés correspond chaque graduation 90° ° 0 4 ° 0 3 20° 10° 0°

Maintenant, vous allez avoir un rapporteur gradué pour mesurer l'angle qui va vous être distribué. Essayez de trouver comment utiliser le rapporteur.

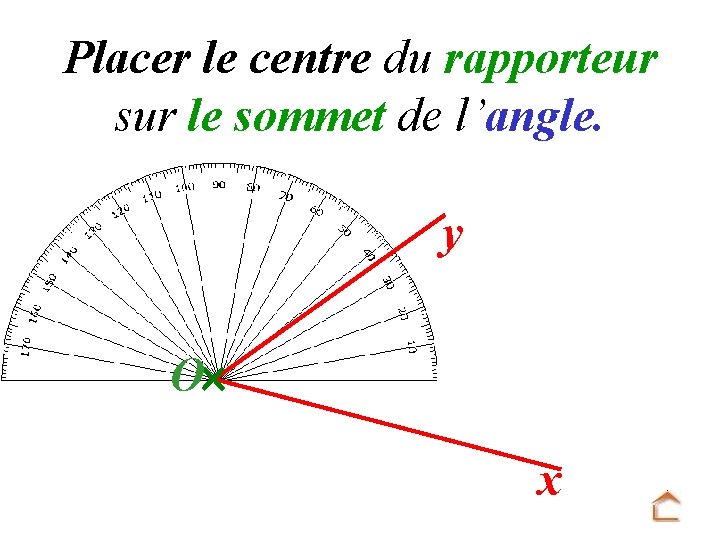
Placer le centre du rapporteur sur le sommet de l’angle. y O x

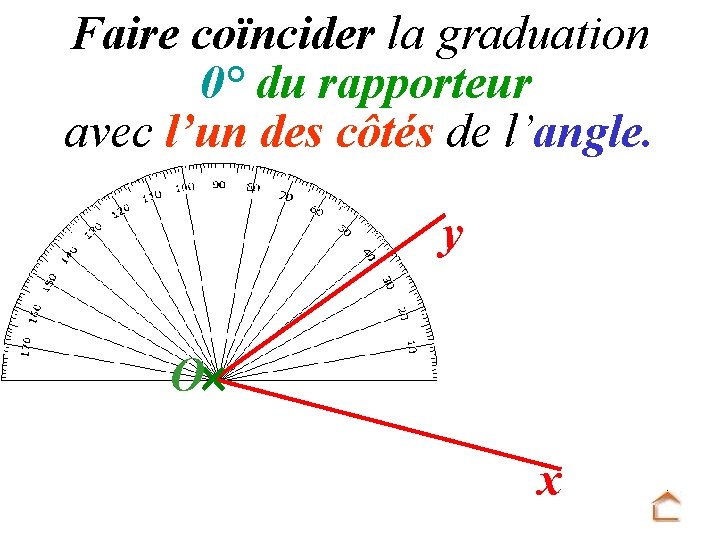
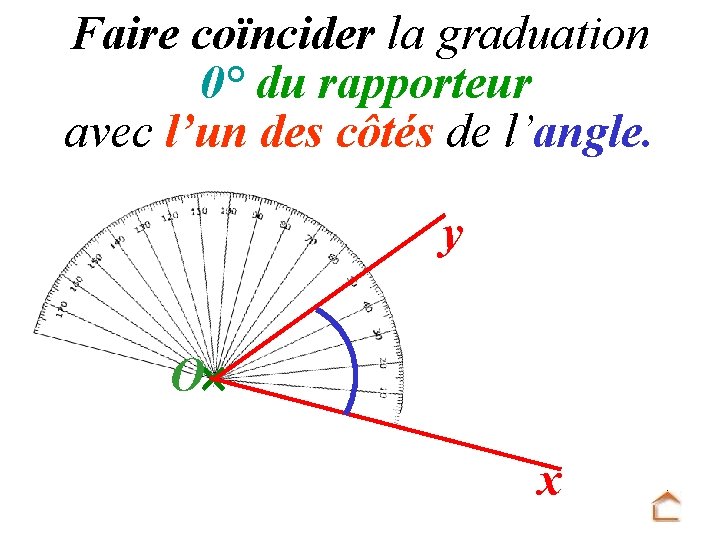
Faire coïncider la graduation 0° du rapporteur avec l’un des côtés de l’angle. y O x

Faire coïncider la graduation 0° du rapporteur avec l’un des côtés de l’angle. y O x

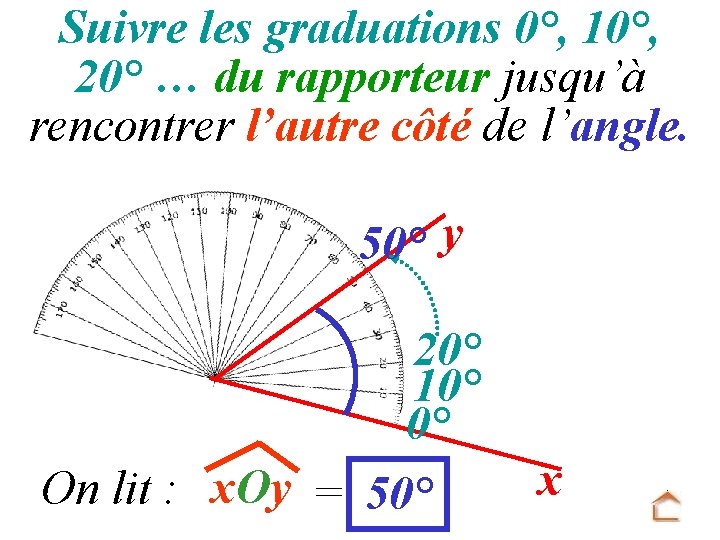
Suivre les graduations 0°, 10°, 20° … du rapporteur jusqu’à rencontrer l’autre côté de l’angle. 50° y 20° 10° 0° On lit : x. Oy = 50° x

Remarque : Il est parfois utile de prolonger un côté pour pouvoir mesurer. 50° y 20° 10° 0° On lit : x. Oy = 50° x

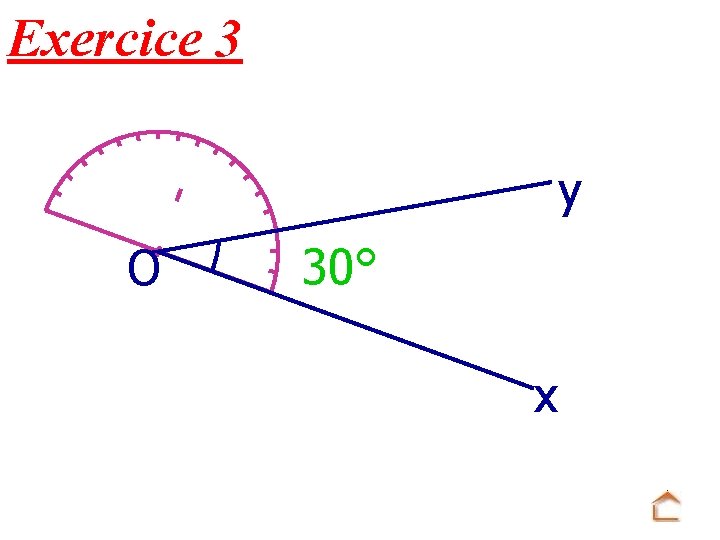
Exercice 3 y O 30° x

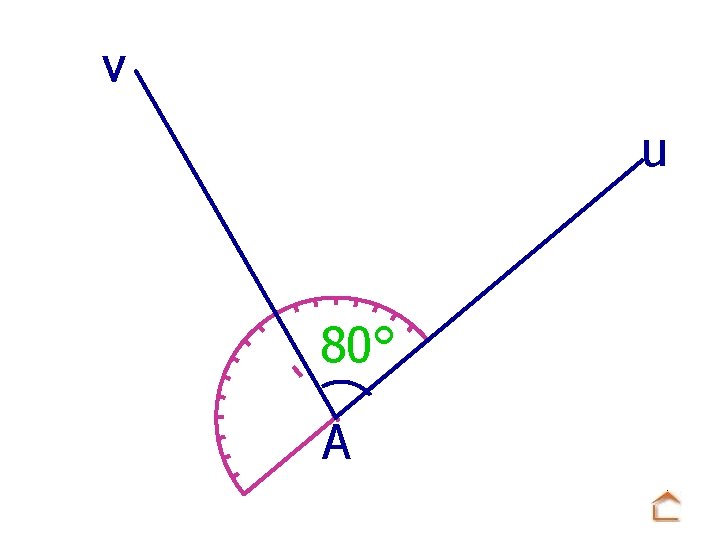
v u 80° A

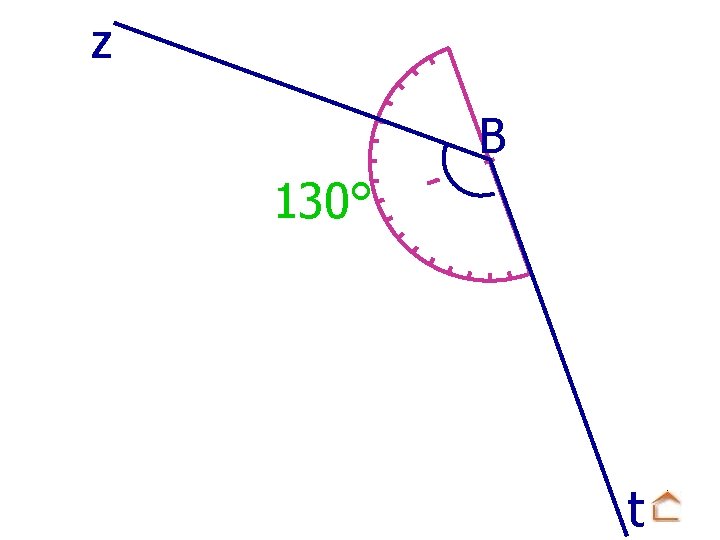
z B 130° t

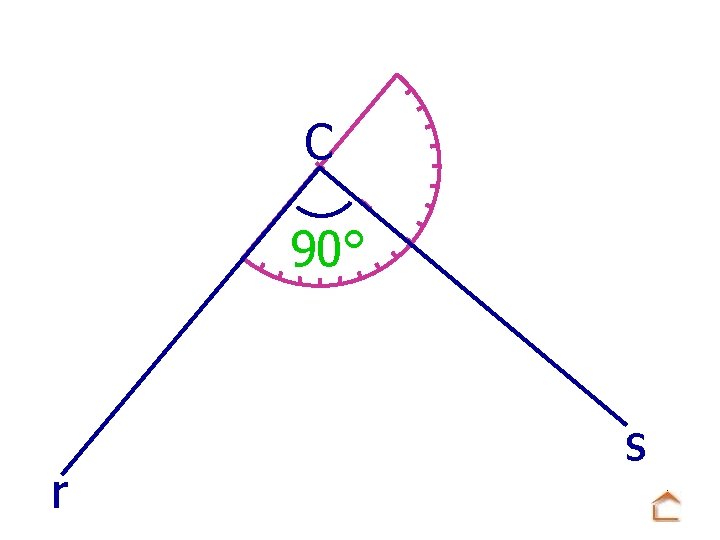
C 90° r s

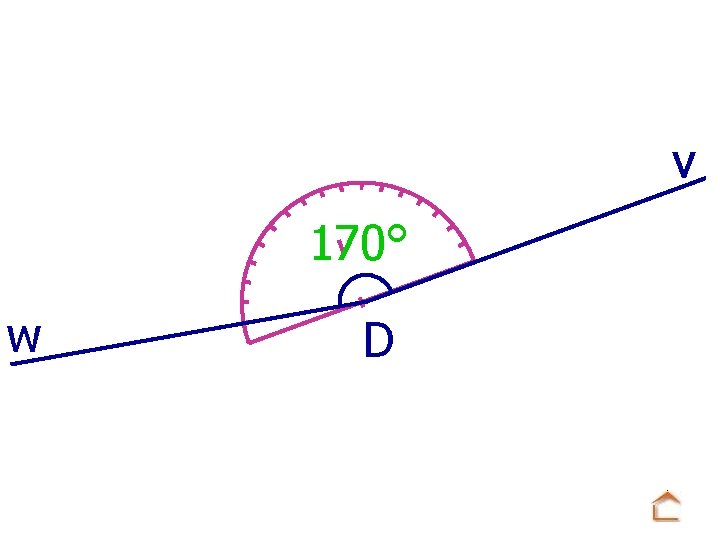
v 170° w D

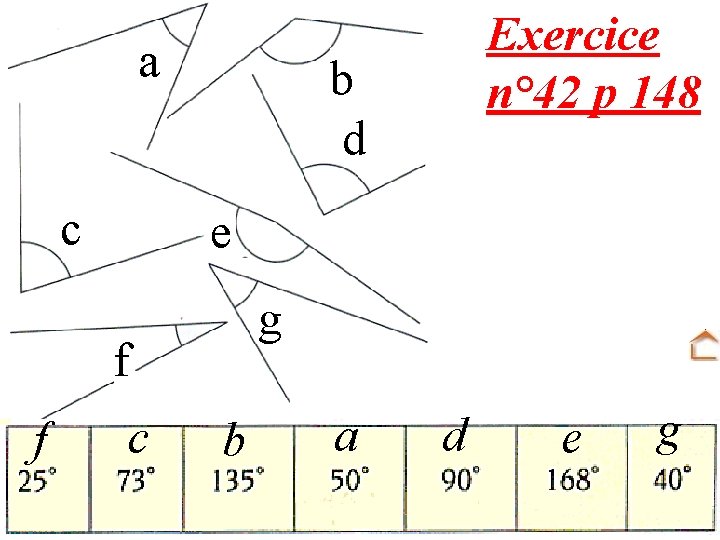
a c b d e g f f Exercice n° 42 p 148 c b a d e g

5. Construction d’angles a) Construction d’un angle de mesure donnée b) Reproduction d’un angle

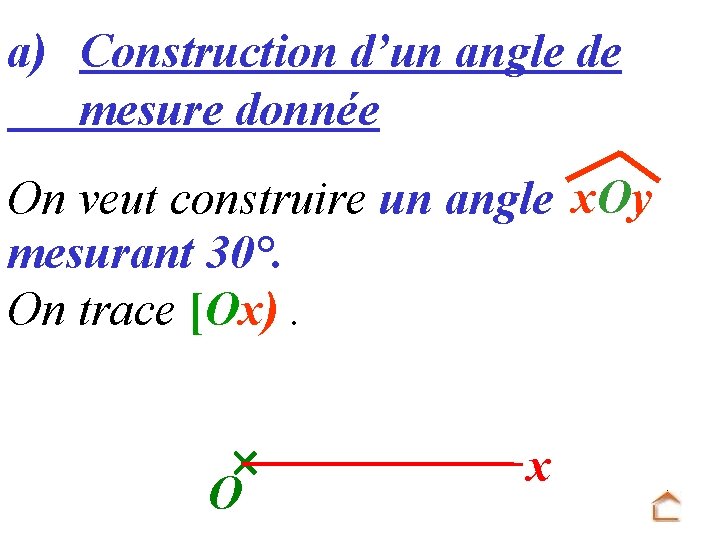
a) Construction d’un angle de mesure donnée On veut construire un angle x. Oy mesurant 30°. On trace [Ox). O x

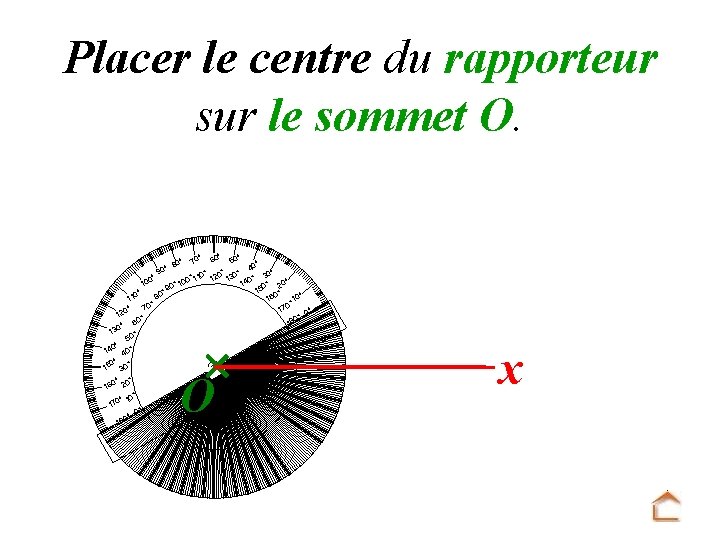
Placer le centre du rapporteur sur le sommet O. ° ° 50 ° 40 9 ° 0° 0 2 ° 1 1 13 40° 3 0° ° 00 1 ° 10 ° 1 1 0 20 90 15 ° 0° 0° ° 0 8 1 1 10 16 0° 0° 7 7 ° 1 0 0° 12 ° 0° 80 6 1 0° 13 ° 50 ° 0 14 40° 0° 15 30° ° 80 0° 0° 0° 16 2 ° 0° 10 17 0° 0° 18 ° 70 60 O x

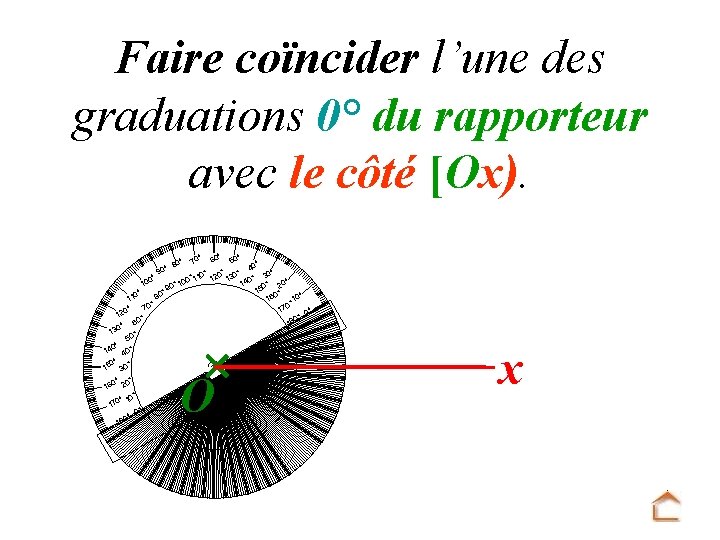
Faire coïncider l’une des graduations 0° du rapporteur avec le côté [Ox). ° ° 50 ° 40 9 ° 0° 0 2 ° 1 1 13 40° 3 0° ° 00 1 ° 10 ° 1 1 0 20 90 15 ° 0° 0° ° 0 8 1 1 10 16 0° 0° 7 7 ° 1 0 0° 12 ° 0° 80 6 1 0° 13 ° 50 ° 0 14 40° 0° 15 30° ° 80 0° 0° 0° 16 2 ° 0° 10 17 0° 0° 18 ° 70 60 O x

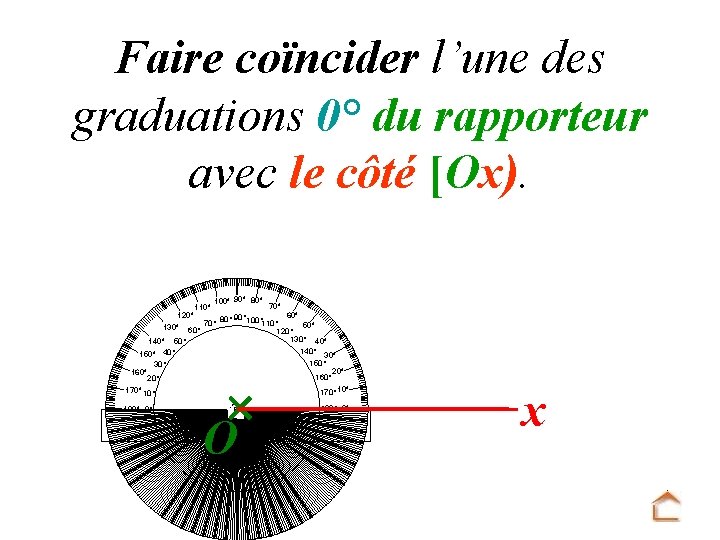
Faire coïncider l’une des graduations 0° du rapporteur avec le côté [Ox). 100° 90° 80° 70° 60° 120° 90° 100° 80° 70° 110° 50° 130° 60° 120° 130° 40° 140° 50° 140° 150° 40° 30° 150° 30° 20° 160° 20° 170° 10° 110° 180° 0° O 180° 0° x

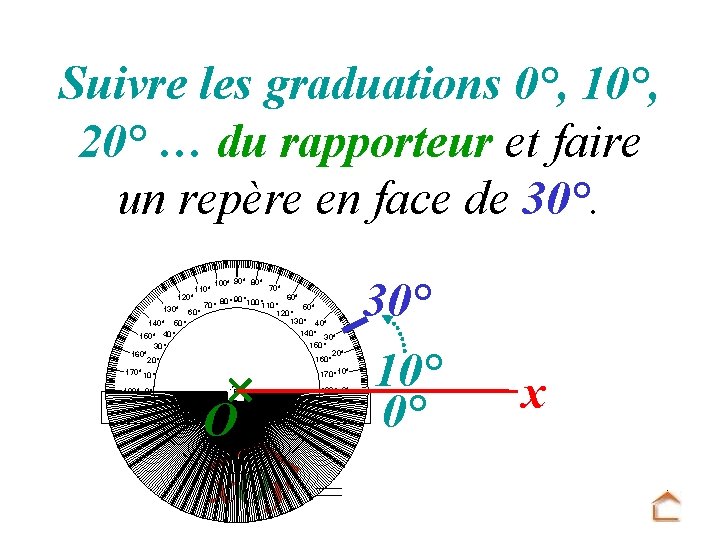
Suivre les graduations 0°, 10°, 20° … du rapporteur et faire un repère en face de 30°. 100° 90° 80° 70° 60° 120° 90° 100° 80° 70° 110° 50° 130° 60° 120° 130° 40° 140° 50° 140° 150° 40° 30° 150° 30° 20° 160° 20° 110° 170° 180° 0° O x. Oy = 170° 180° 0° 30° 10° 0° x

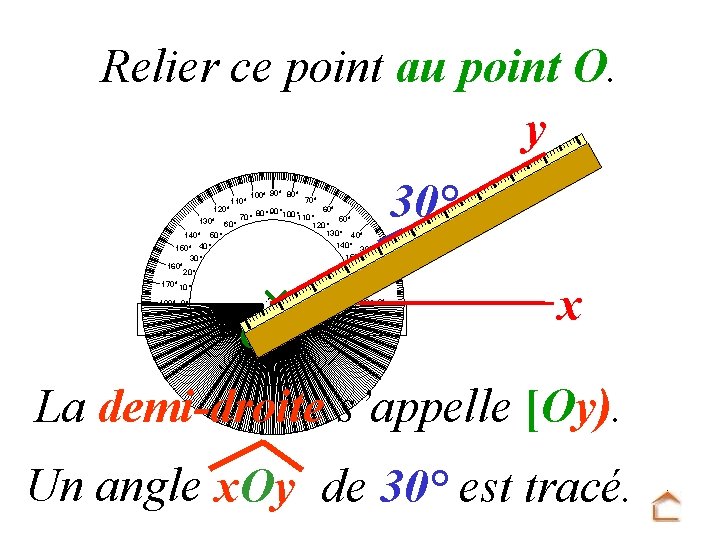
Relier ce point au point O. y 100° 90° 80° 70° 60° 120° 90° 100° 80° 70° 110° 50° 130° 60° 120° 130° 40° 140° 50° 140° 150° 40° 30° 150° 30° 20° 160° 20° 110° 170° 180° 0° O 170° 180° 0° 30° x La demi-droite s’appelle [Oy). Un angle x. Oy de 30° est tracé.

Exercice 5 1) Dans chaque cas, construis un angle dont la mesure est : a)70° b) 110° c) 20° d)160° 2) Pour chacun des angles, indique s’il est aigu ou obtus.

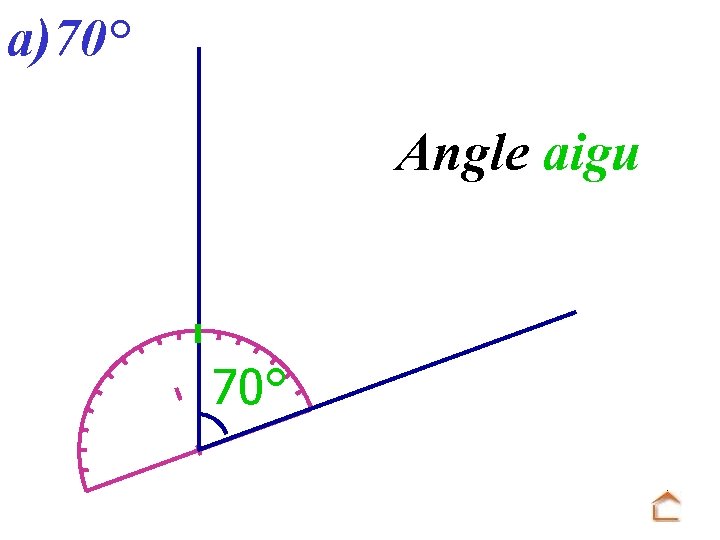
a)70° Angle aigu 70°

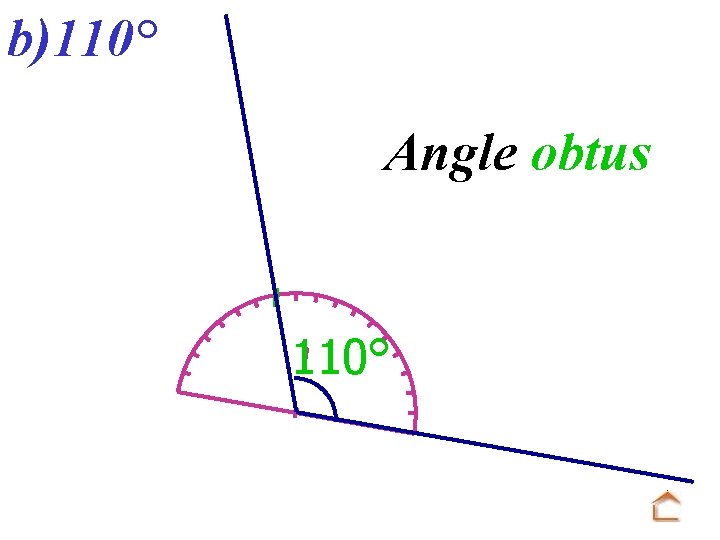
b)110° Angle obtus 110°

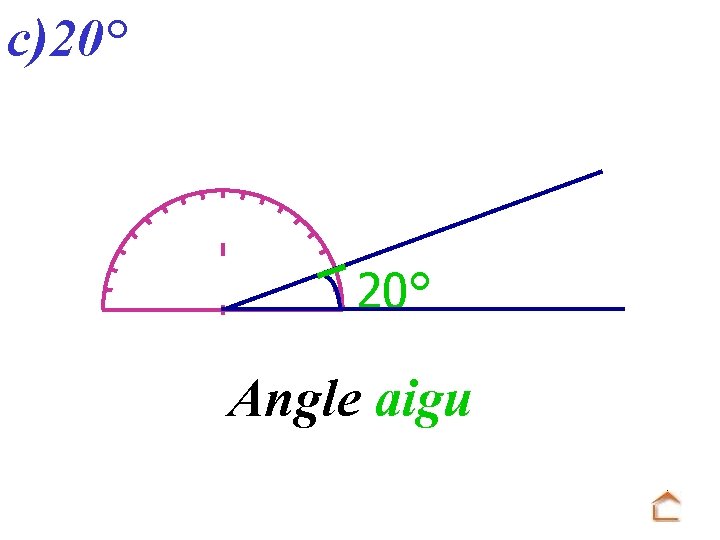
c)20° Angle aigu

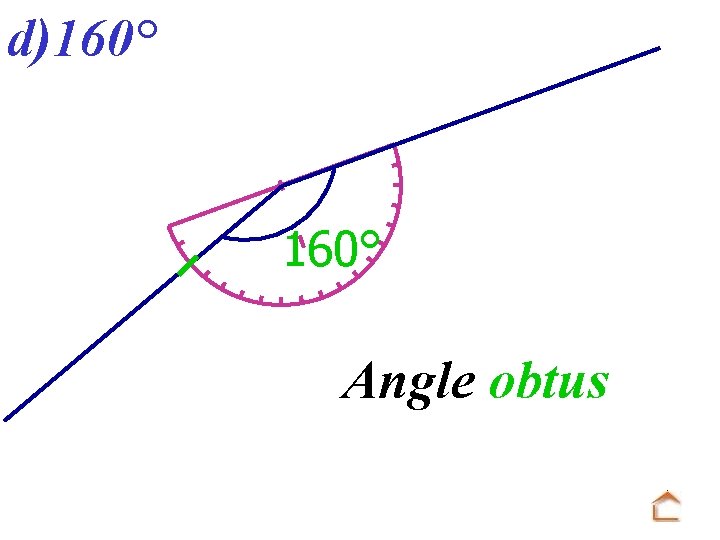
d)160° Angle obtus

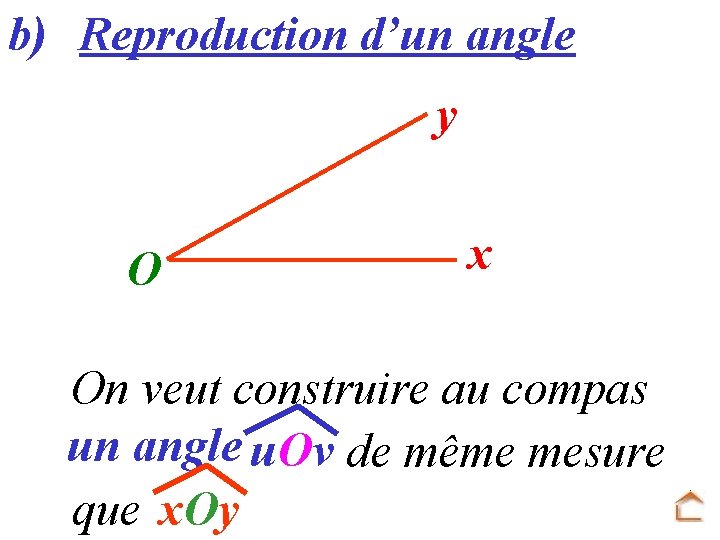
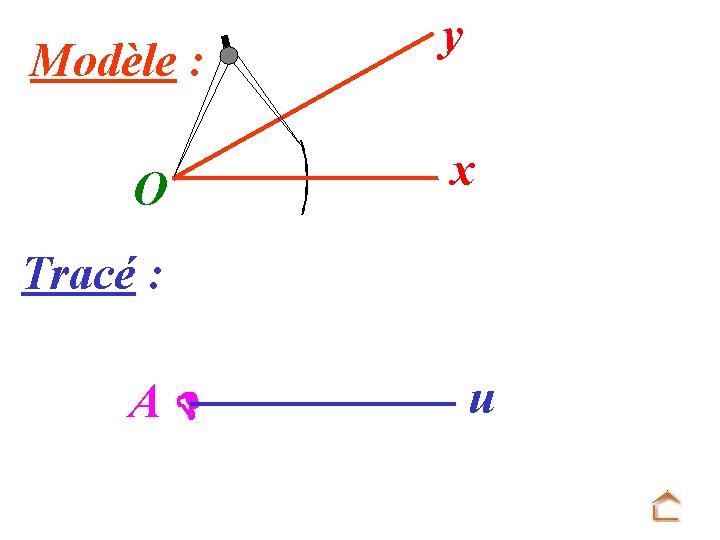
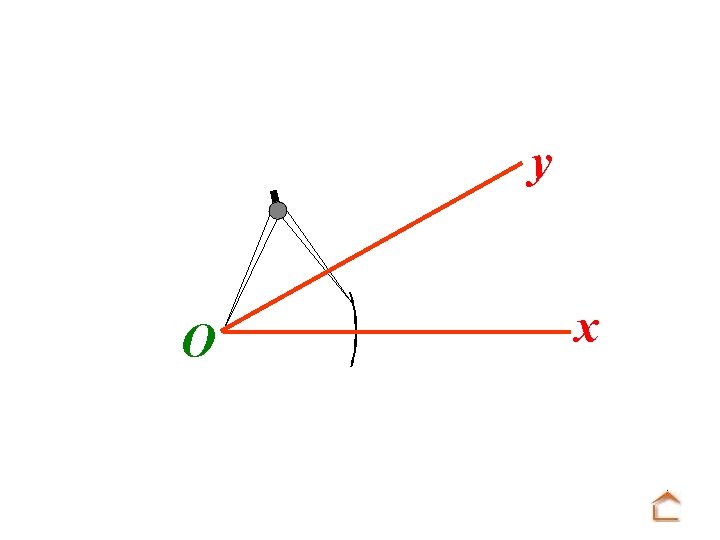
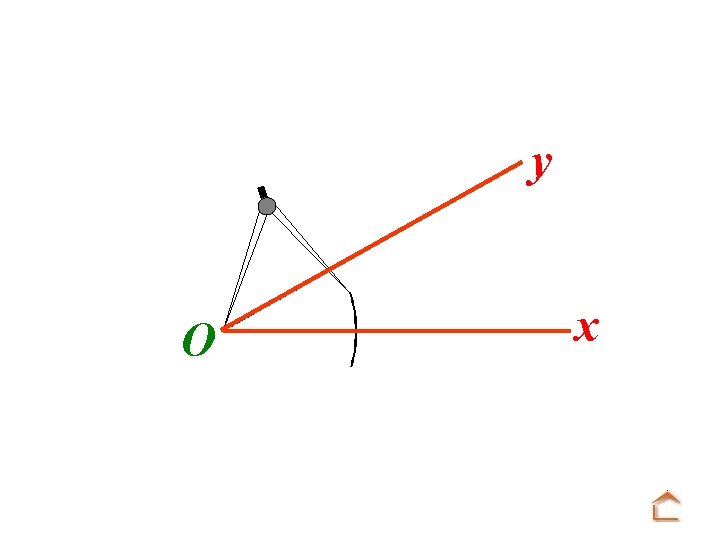
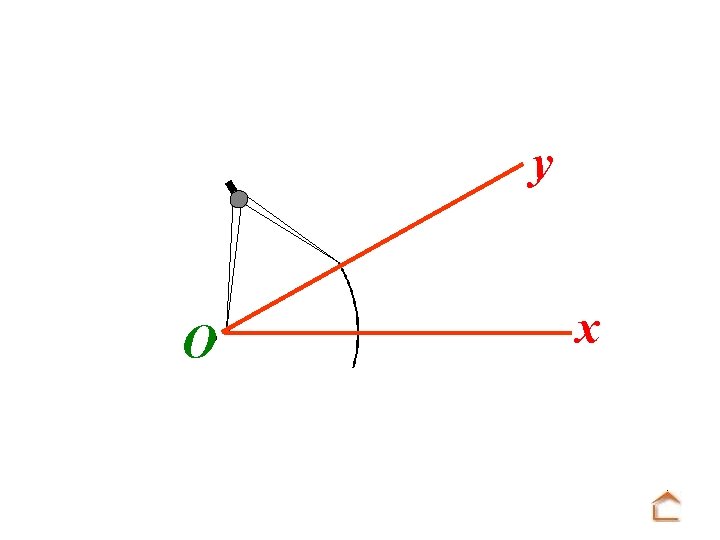
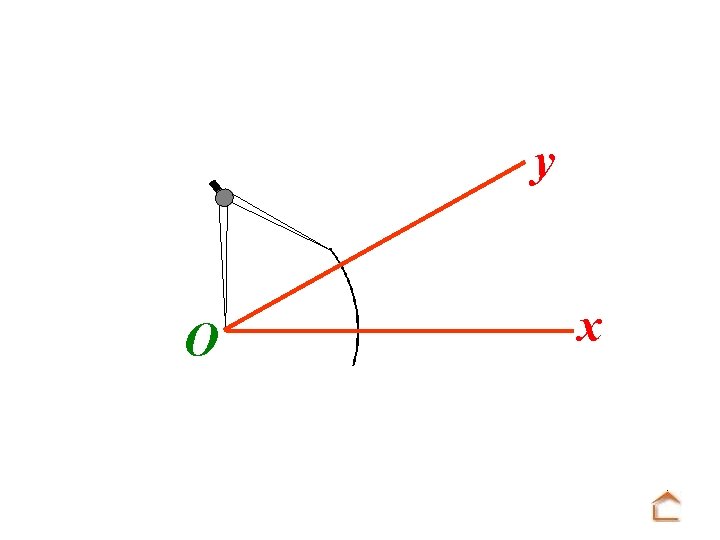
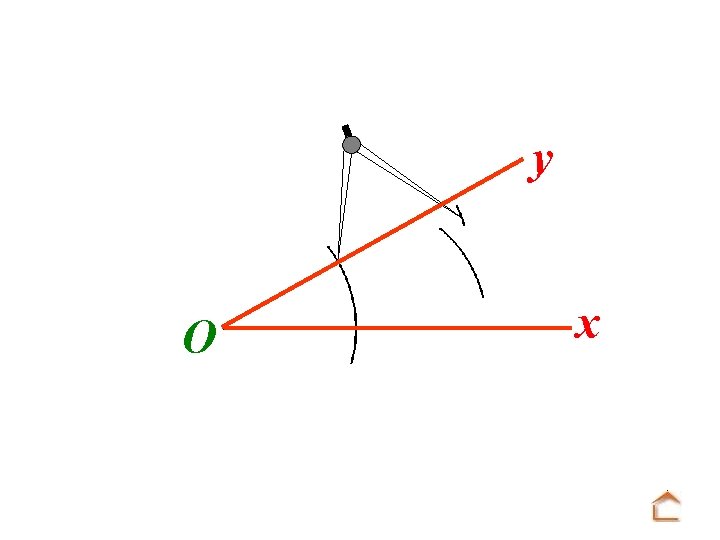
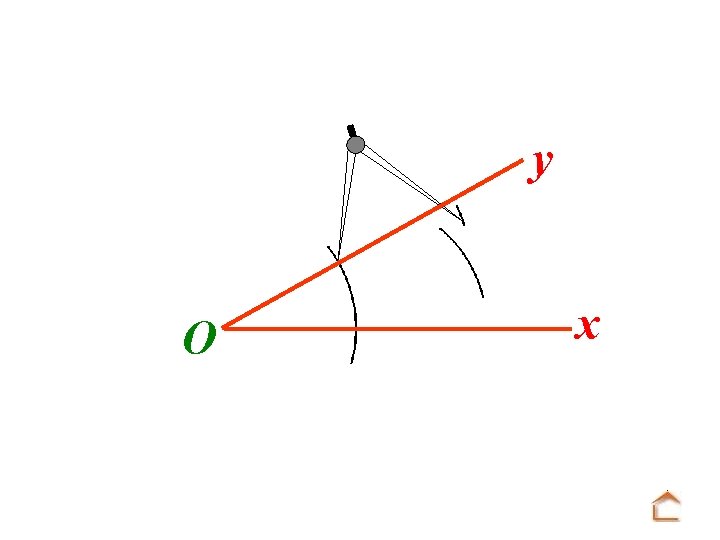
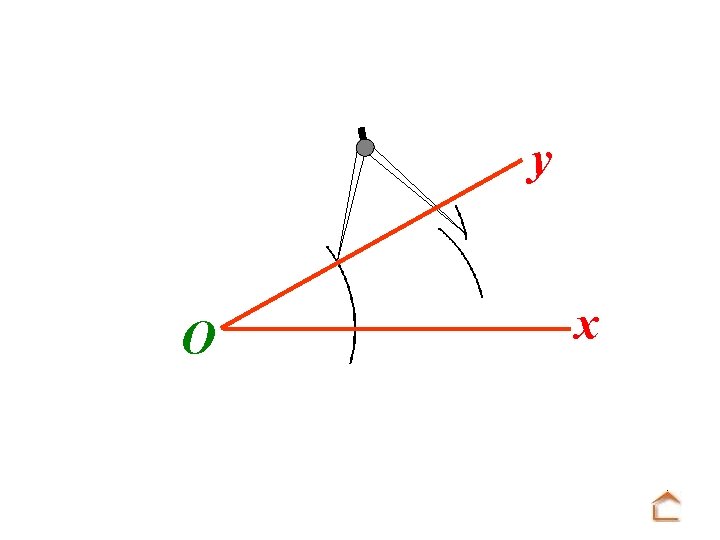
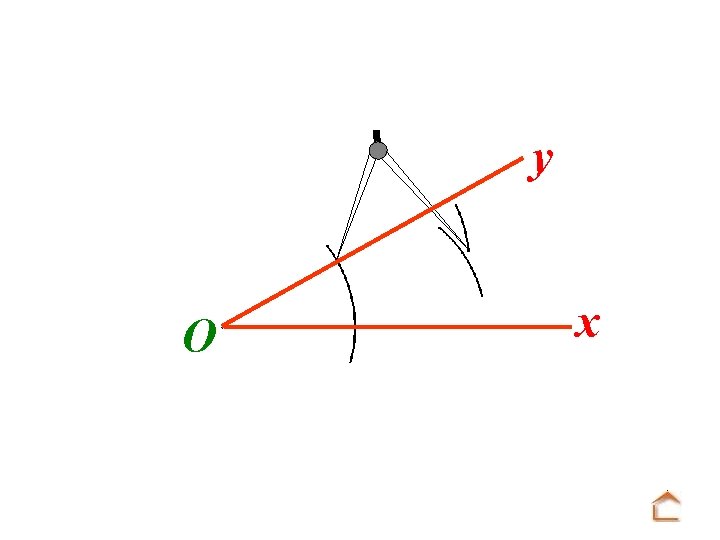
b) Reproduction d’un angle y O x On veut construire au compas un angle u. Ov de même mesure que x. Oy

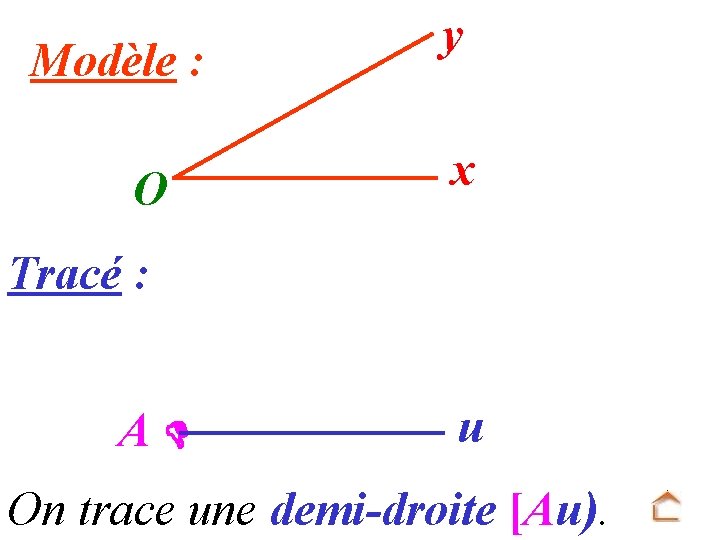
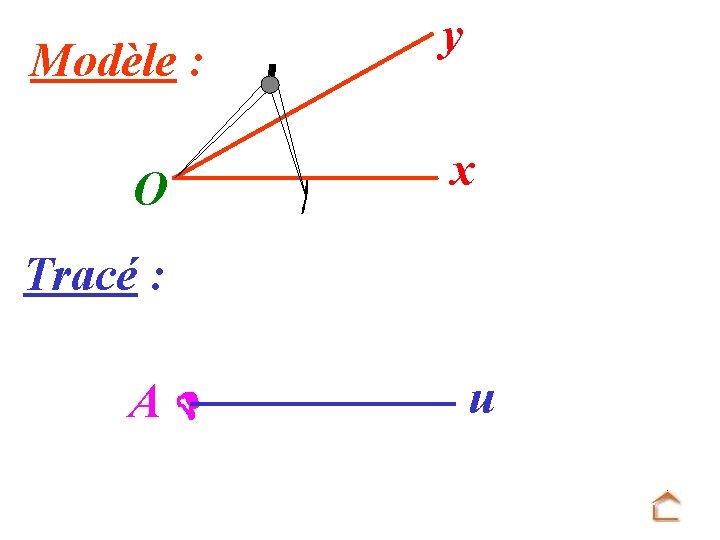
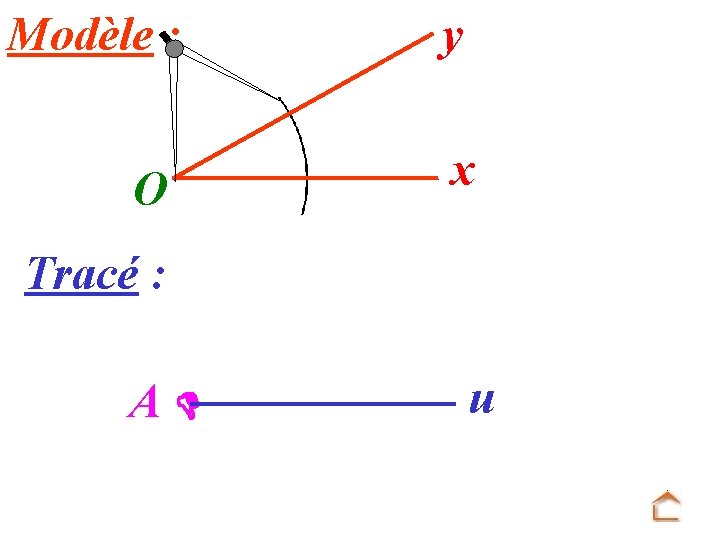
Modèle : O y x Tracé : A u On trace une demi-droite [Au).

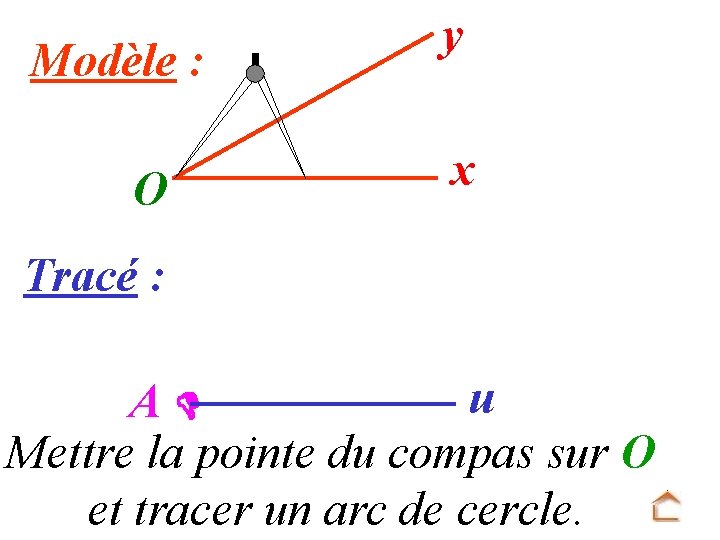
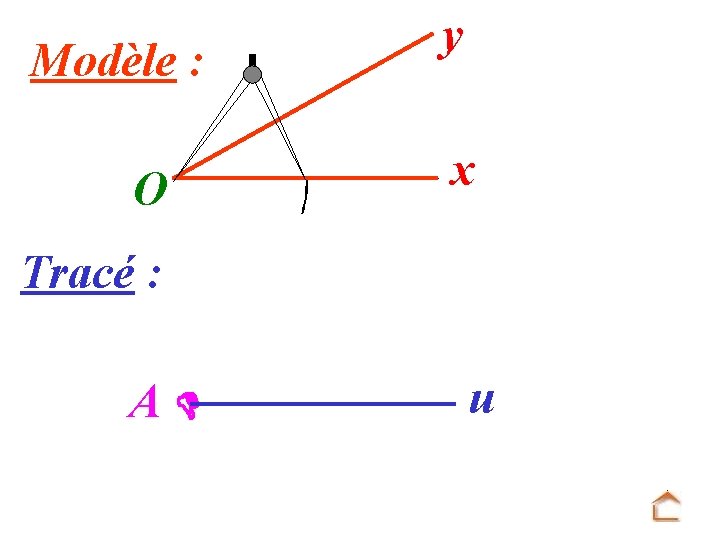
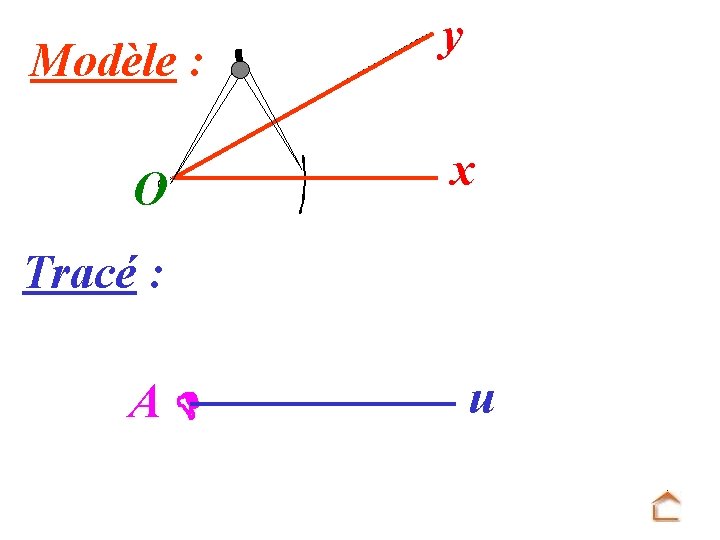
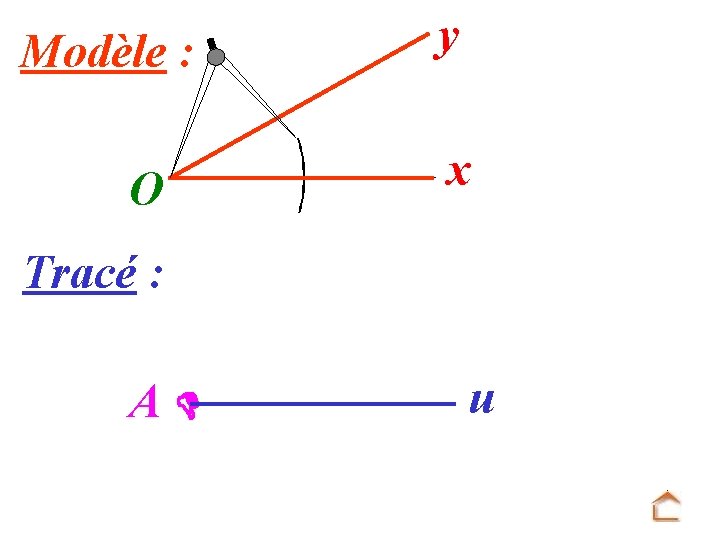
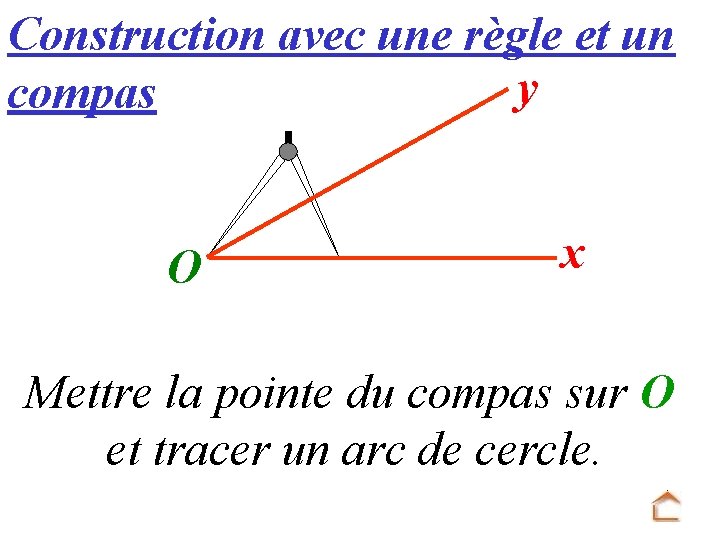
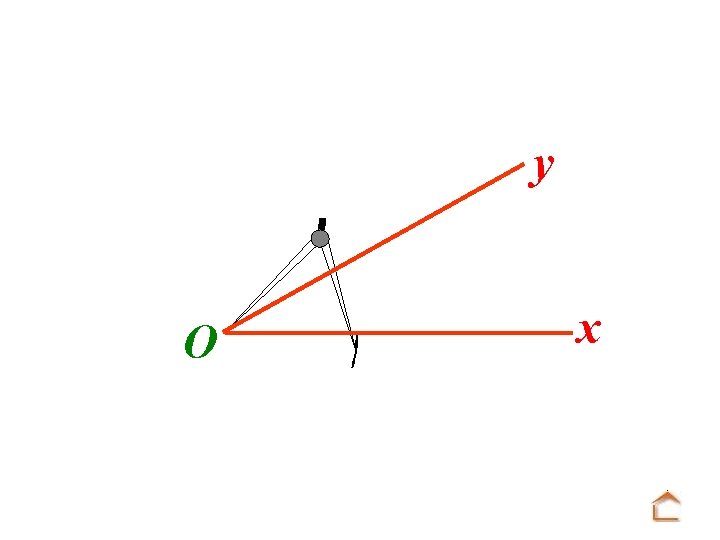
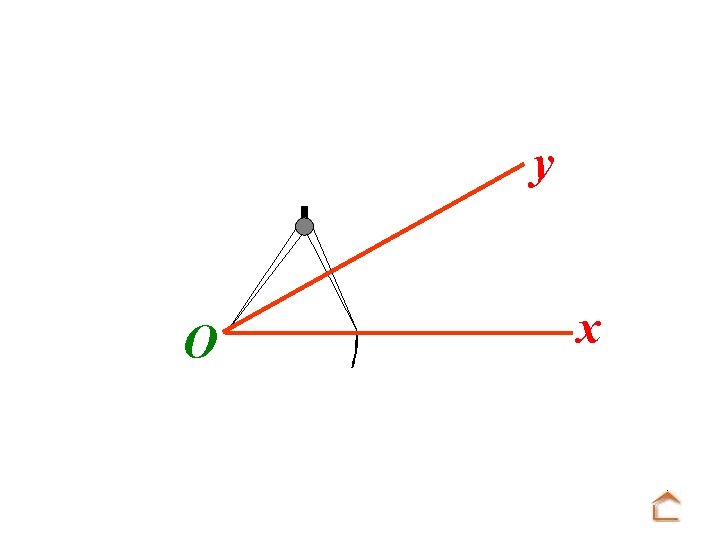
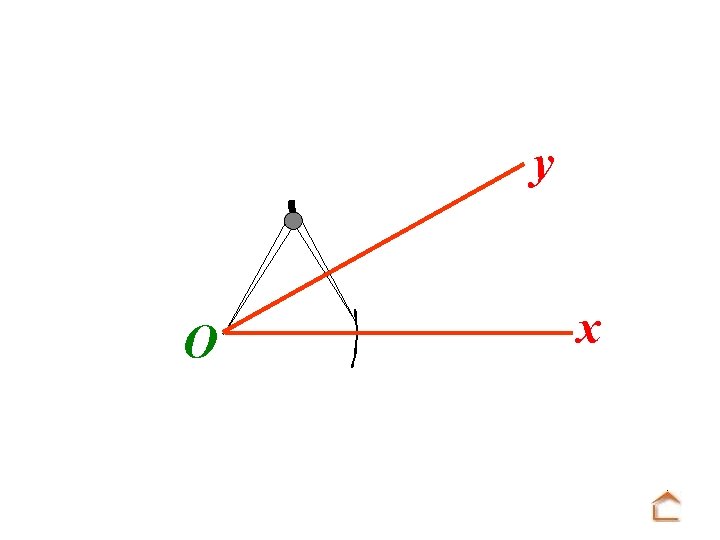
Modèle : O y x Tracé : u A Mettre la pointe du compas sur O et tracer un arc de cercle.

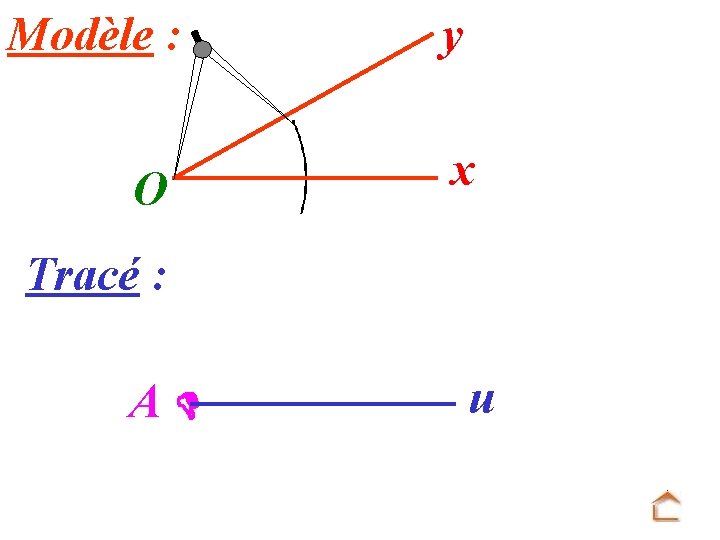
Modèle : O y x Tracé : A u

Modèle : O y x Tracé : A u

Modèle : O y x Tracé : A u

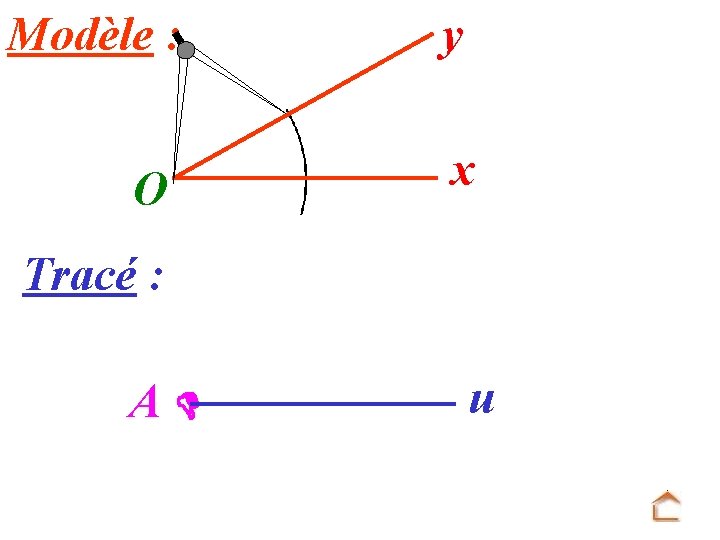
Modèle : O y x Tracé : A u

Modèle : O y x Tracé : A u

Modèle : O y x Tracé : A u

Modèle : O y x Tracé : A u

Modèle : O y x Tracé : A u

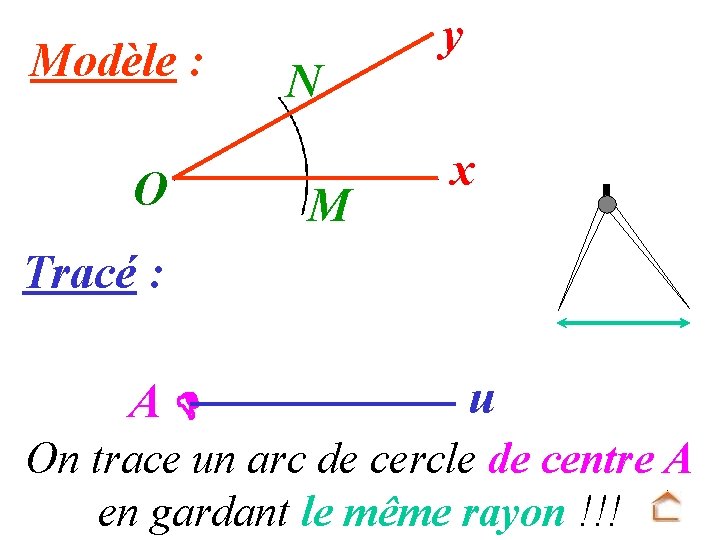
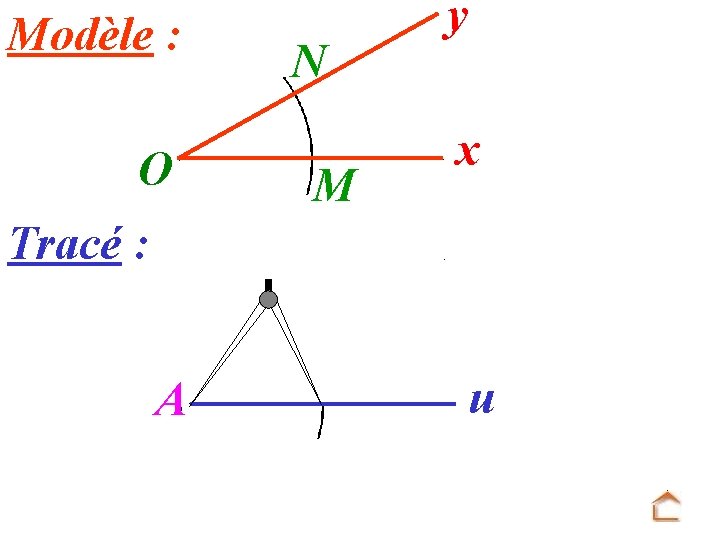
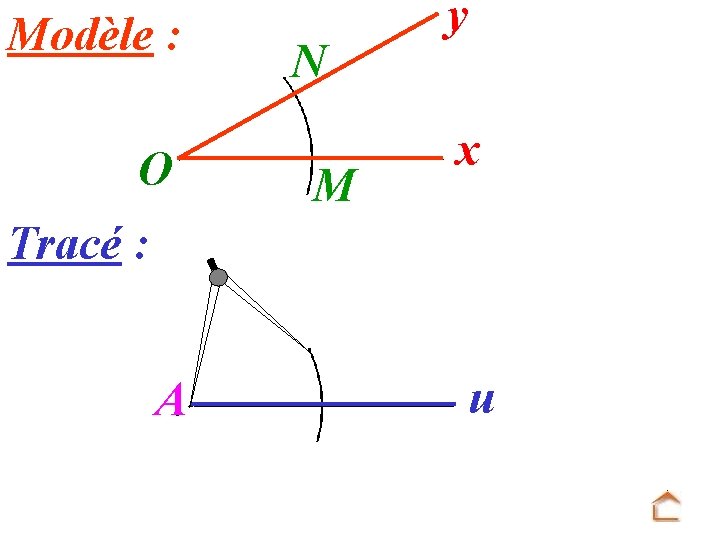
Modèle : O N M y x Tracé : A u On trace un arc de cercle de centre A en gardant le même rayon !!!

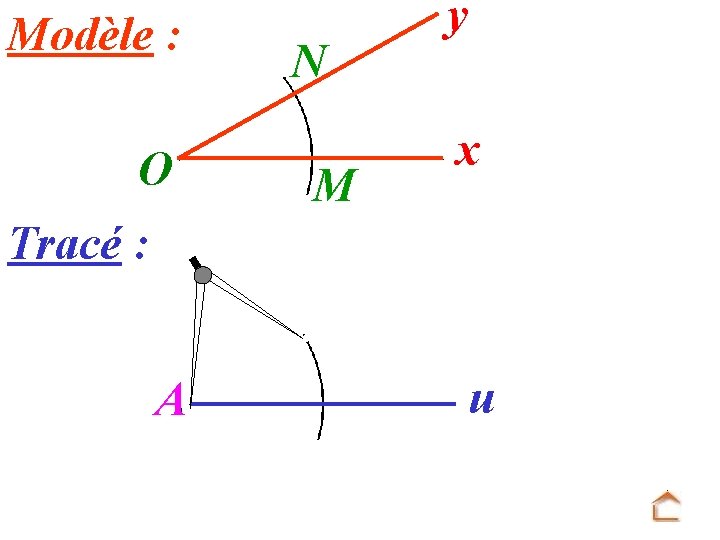
Modèle : O N M y x Tracé : A u

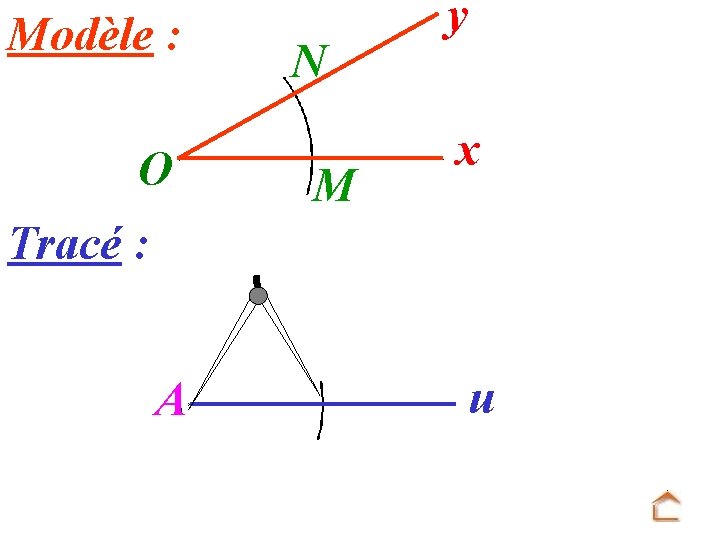
Modèle : O N M y x Tracé : A u

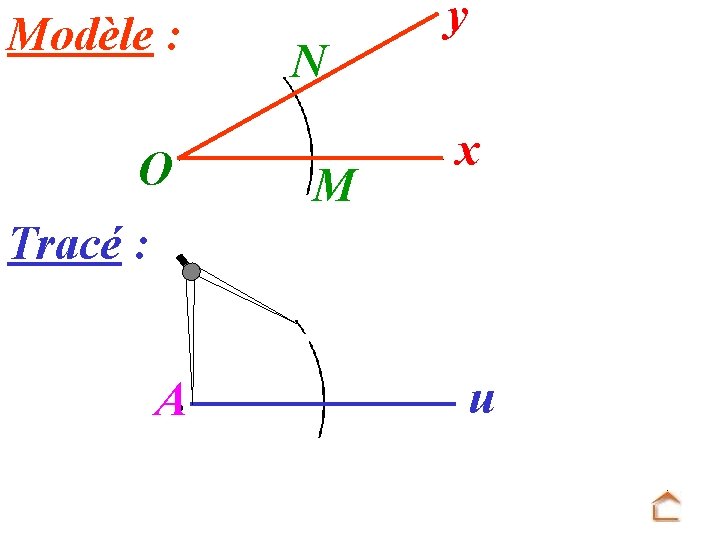
Modèle : O N M y x Tracé : A u

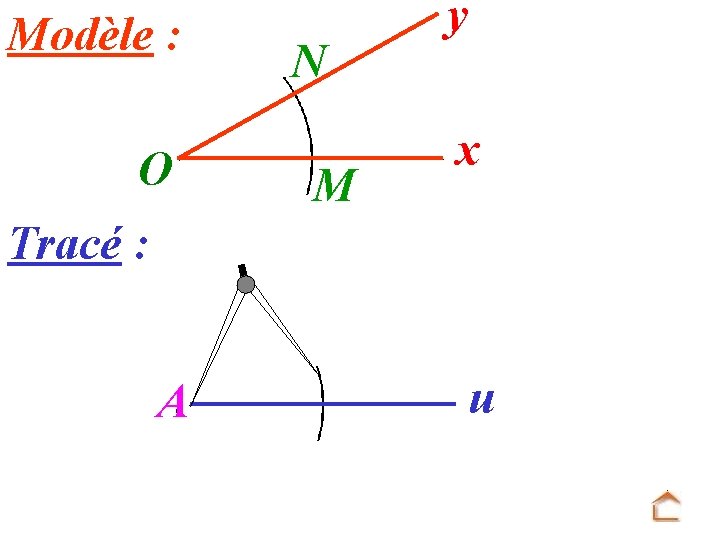
Modèle : O N M y x Tracé : A u

Modèle : O N M y x Tracé : A u

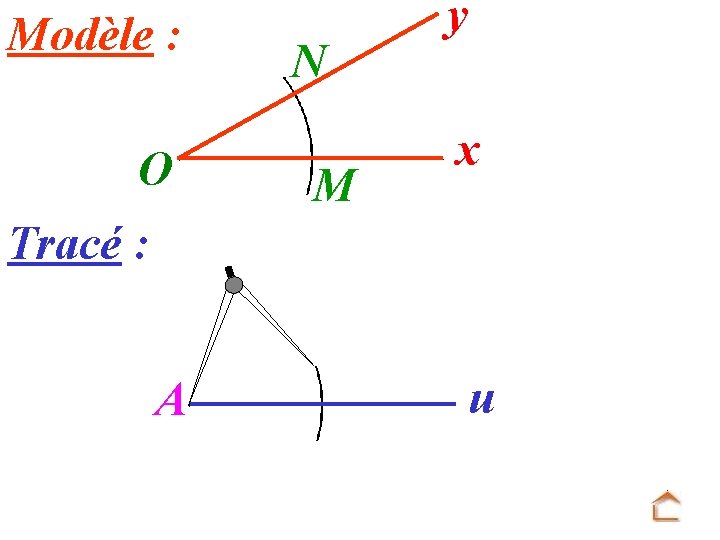
Modèle : O N M y x Tracé : A u

Modèle : O N M y x Tracé : A u

Modèle : O N M y x Tracé : A u

Modèle : O N M y x Tracé : A u

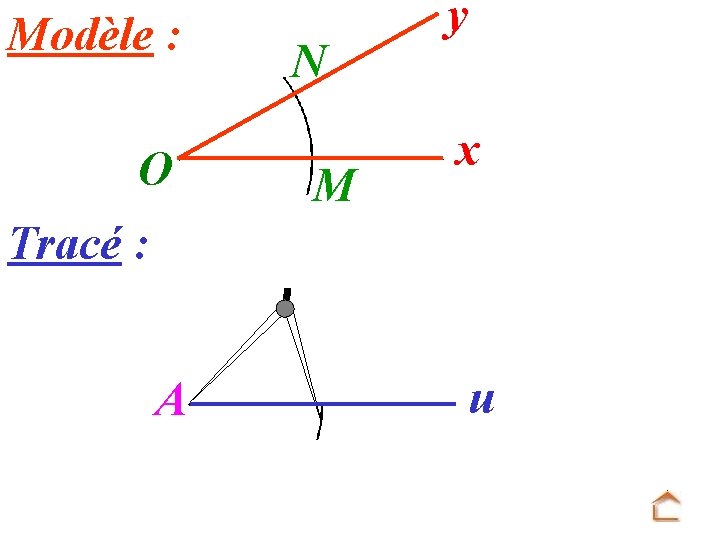
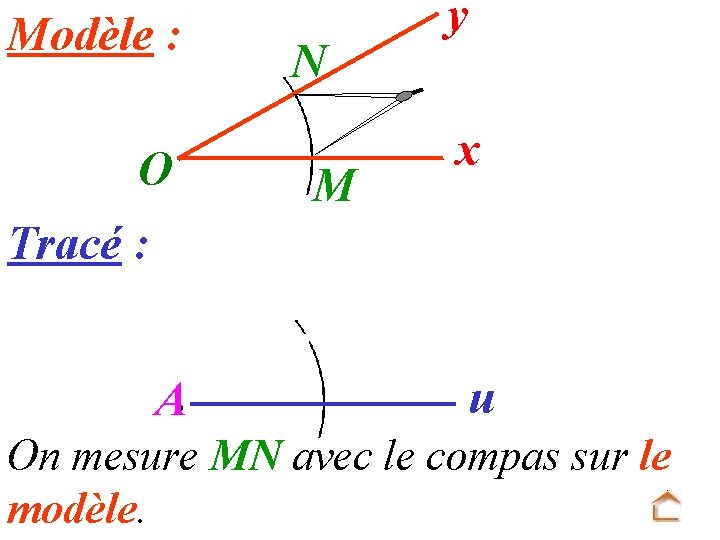
Modèle : O N M y x Tracé : A u On mesure MN avec le compas sur le modèle.

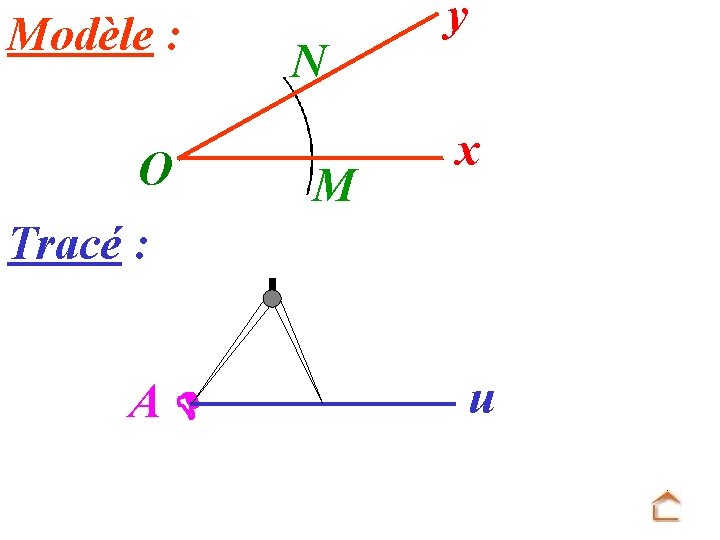
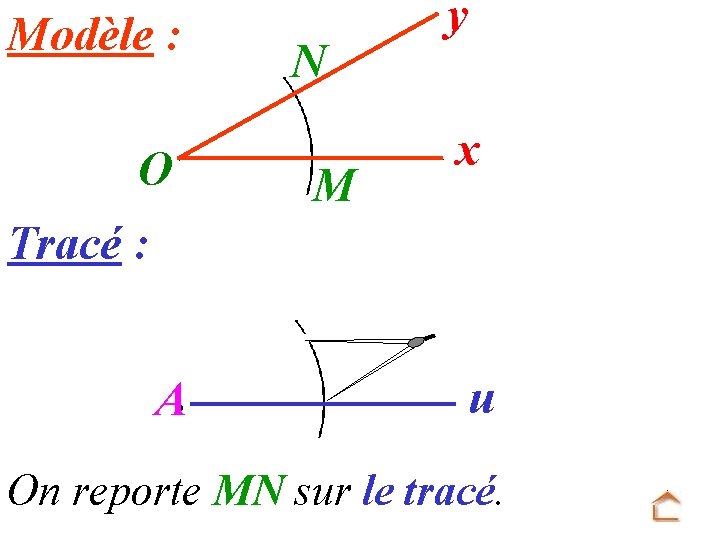
Modèle : O N M y x Tracé : A u On reporte MN sur le tracé.

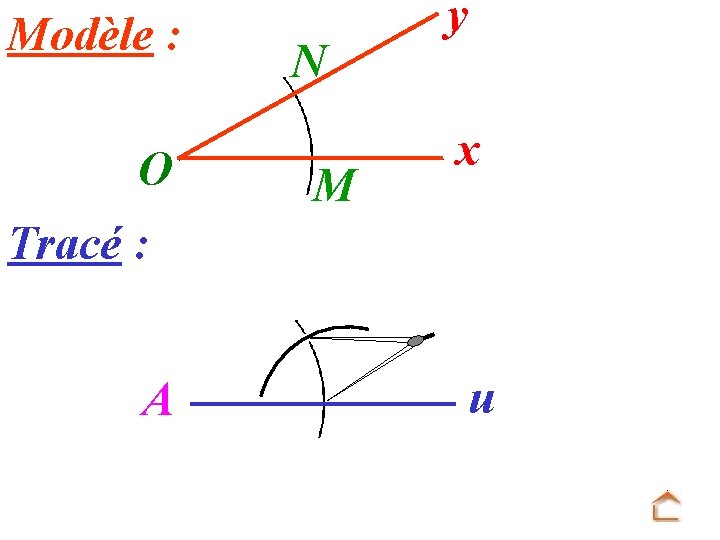
Modèle : O N M y x Tracé : Ai u

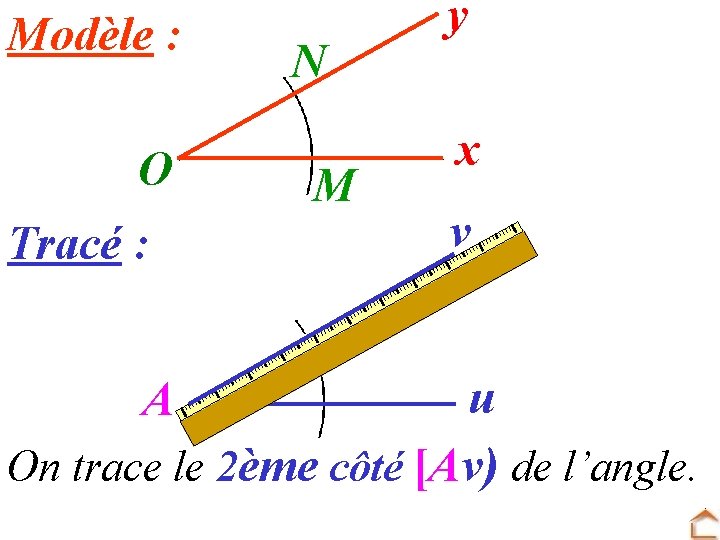
Modèle : O Tracé : N M y x v u On trace le 2ème côté [Av) de l’angle. Ai

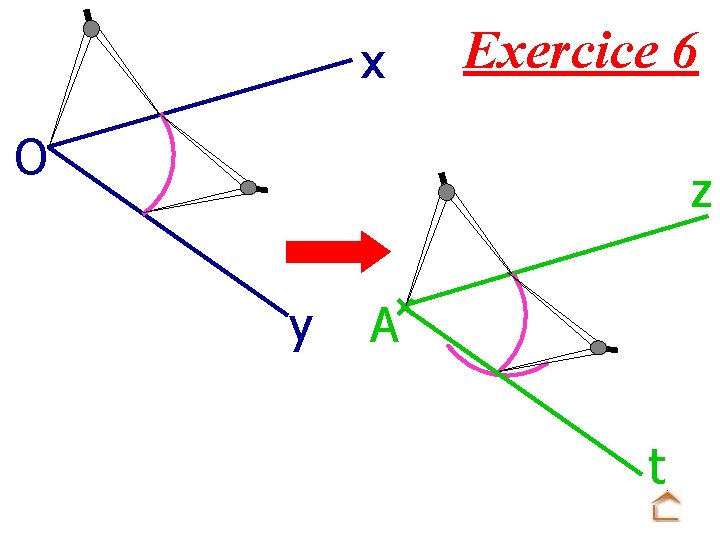
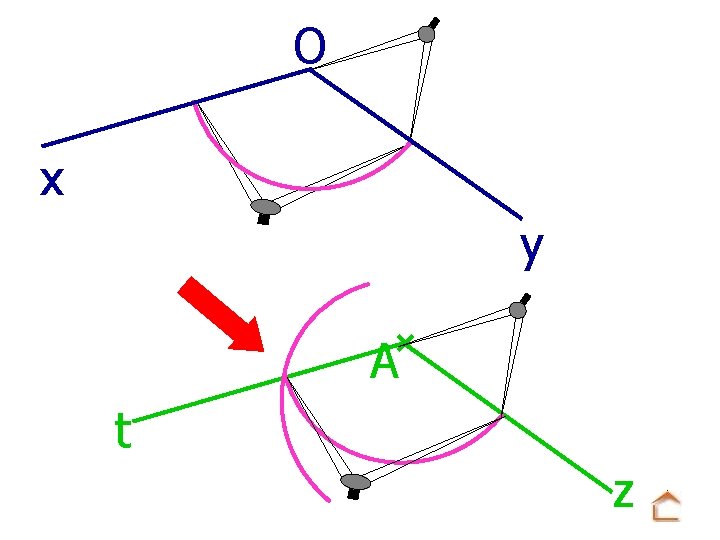
x Exercice 6 O z y A t

O x y A t z

6. Bissectrice d’un angle a) Définition b) Construction - à l ’aide d’un rapporteur et d’une règle - à l ’aide d’un compas et d’une règle

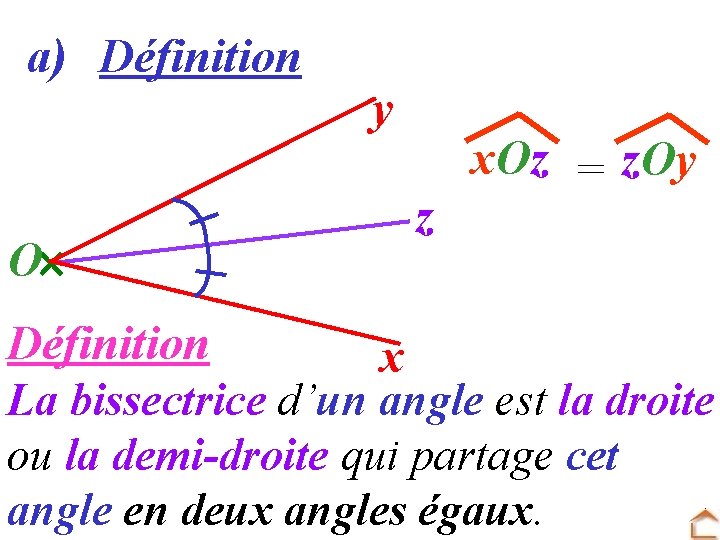
a) Définition O y z x. Oz = z. Oy Définition x La bissectrice d’un angle est la droite ou la demi-droite qui partage cet angle en deux angles égaux.

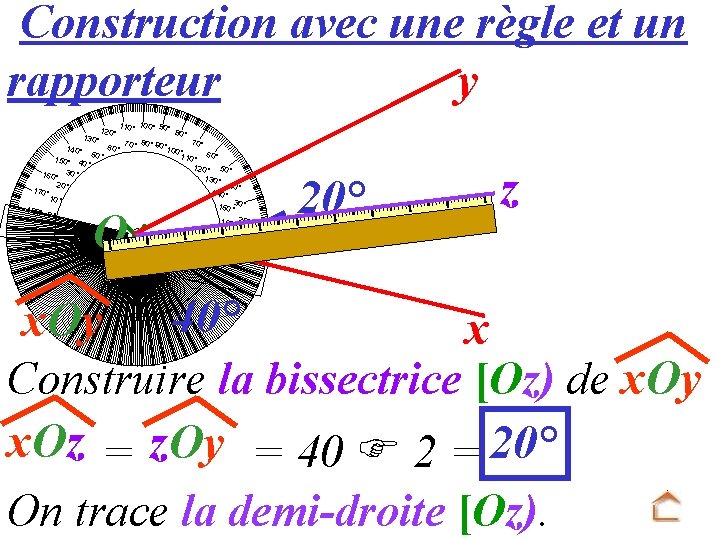
Construction avec une règle et un rapporteur y 100° 90 1 ° 8 120° 10° 0° 130° 70° 80° 90° 60° 140° 100° 50° 1 1 0° 60° 150° 40 ° 120° 50° 160° 30° 130° 20° 40° 170° 140° 10° 3 150° 0° 180° 0° 160° 20° O 20° z 170° 180° 0° x. Oy = 40° x Construire la bissectrice [Oz) de x. Oy x. Oz = z. Oy = 40 2 = 20° On trace la demi-droite [Oz).

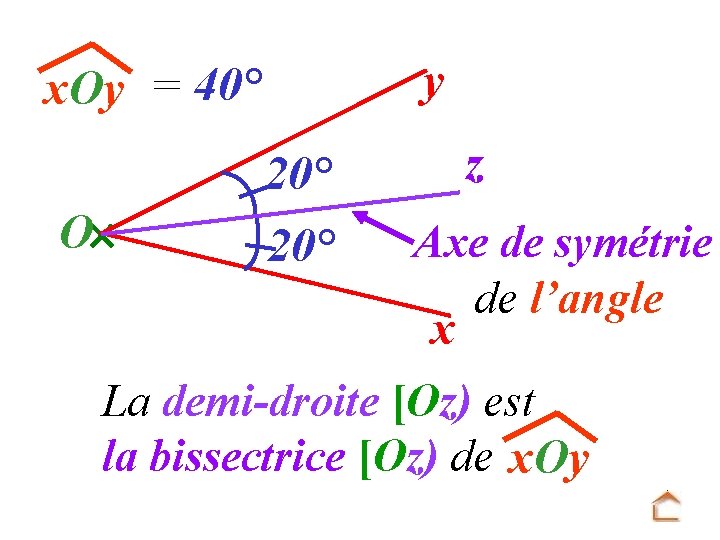
y x. Oy = 40° O 20° z Axe de symétrie de l’angle x La demi-droite [Oz) est la bissectrice [Oz) de x. Oy

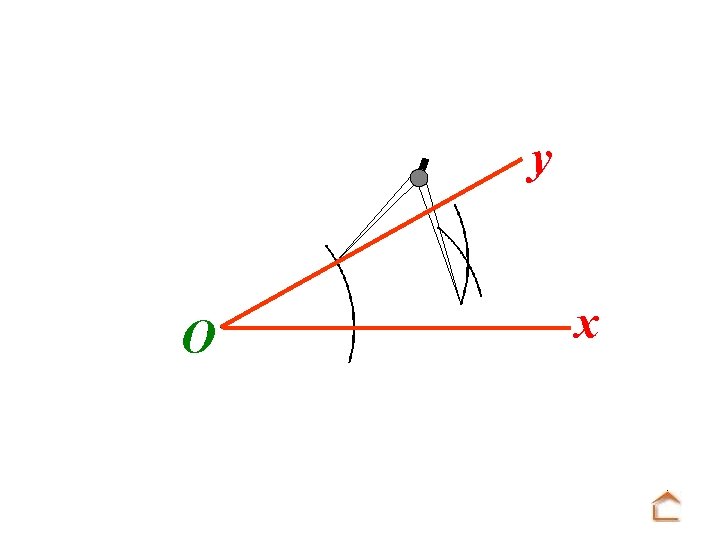
Construction avec une règle et un y compas O x Mettre la pointe du compas sur O et tracer un arc de cercle.

y O x

y O x

y O x

y O x

y O x

y O x

y O x

y O x

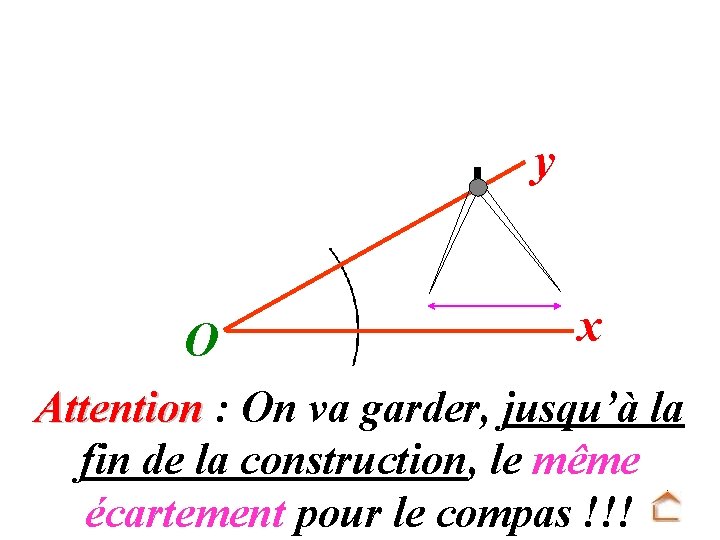
y O x Attention : On va garder, jusqu’à la fin de la construction, le même écartement pour le compas !!!

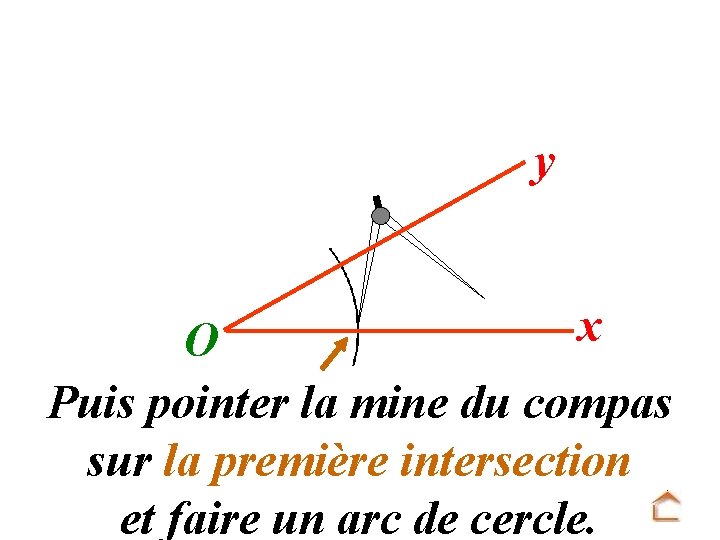
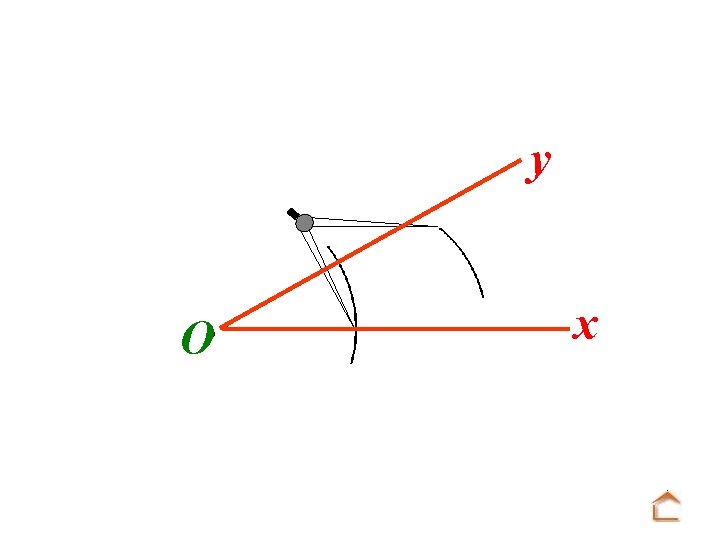
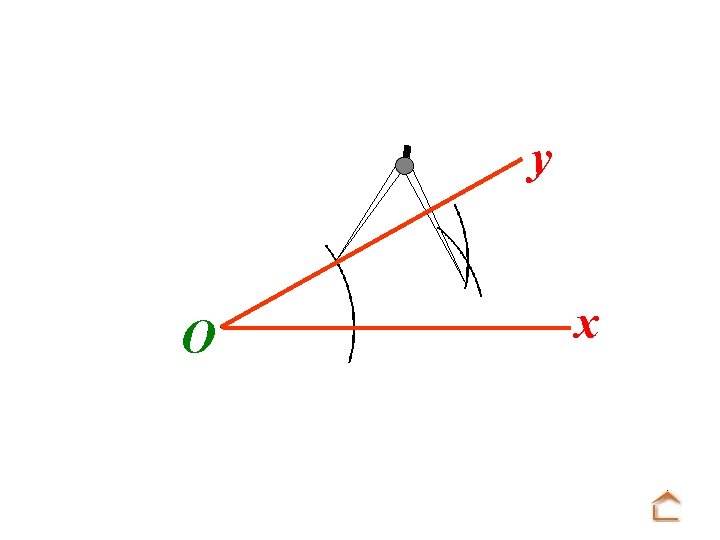
y x O Puis pointer la mine du compas sur la première intersection et faire un arc de cercle.

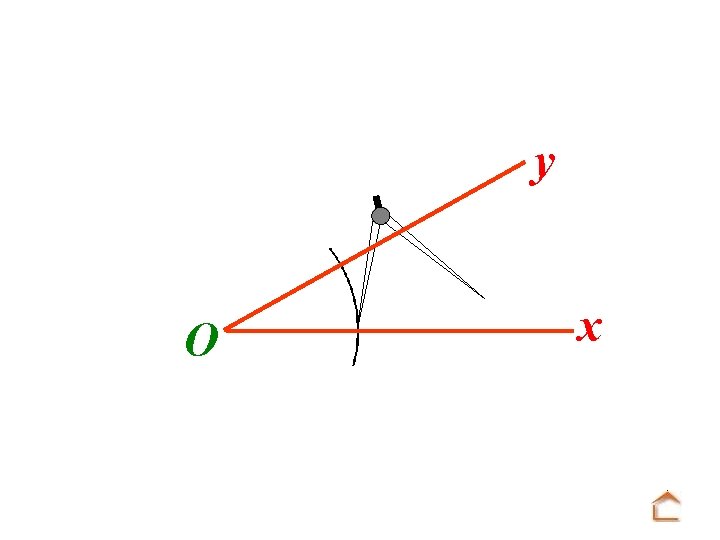
y O x

y O x

y O x

y O x

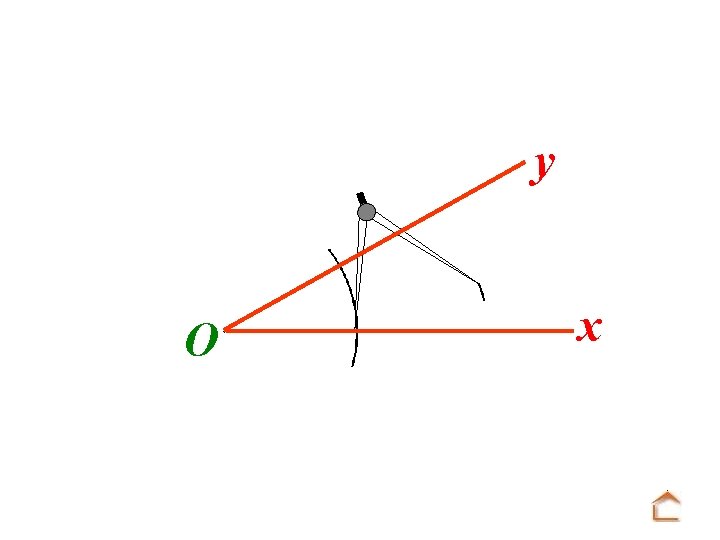
y O x

y O x

y O x

y O x

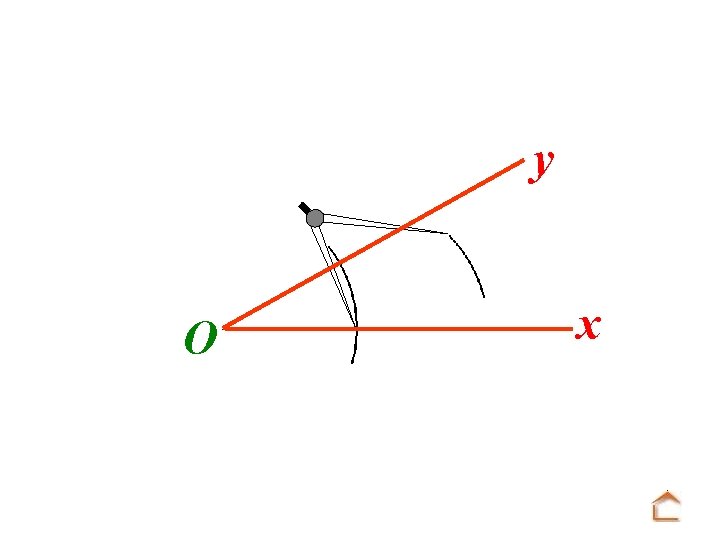
y O x Et donc toujours avec le même écartement. . .

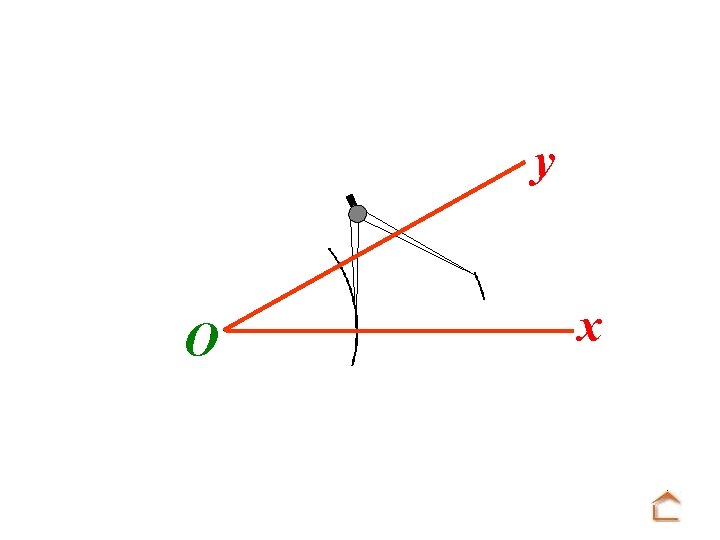
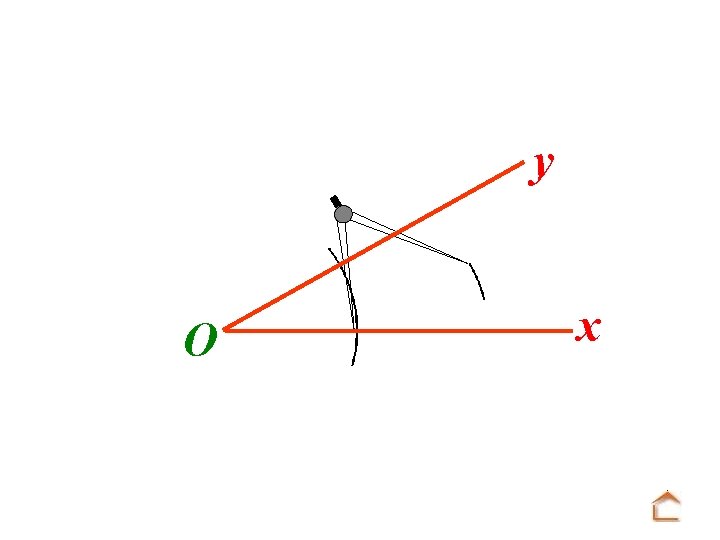
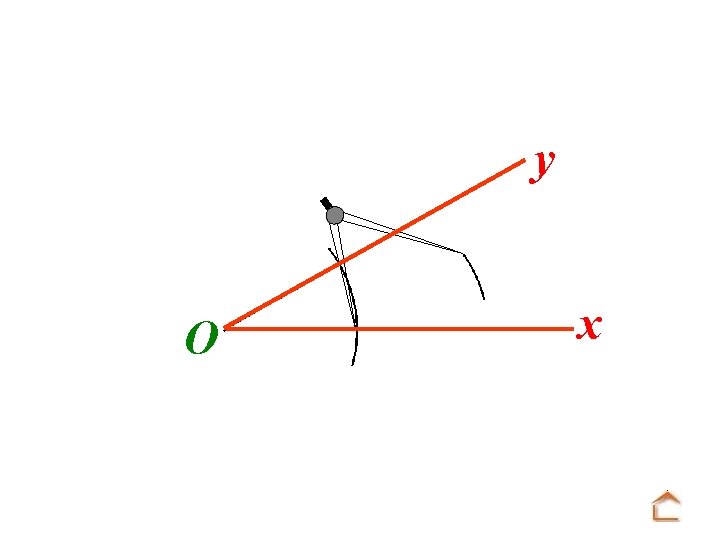
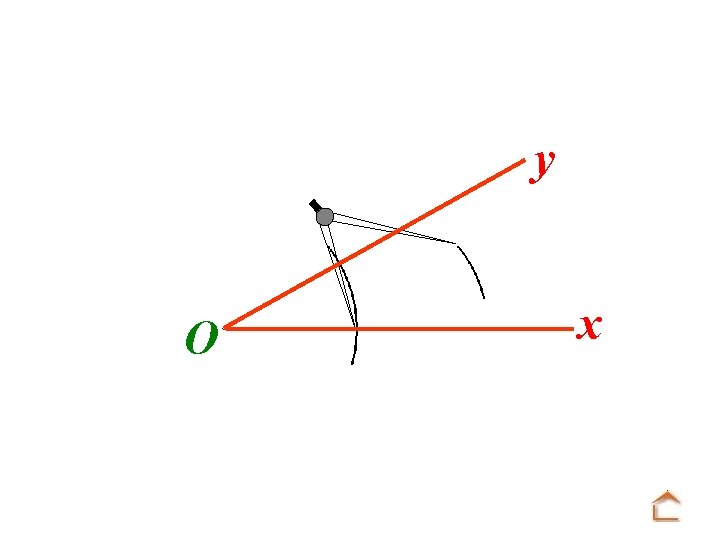
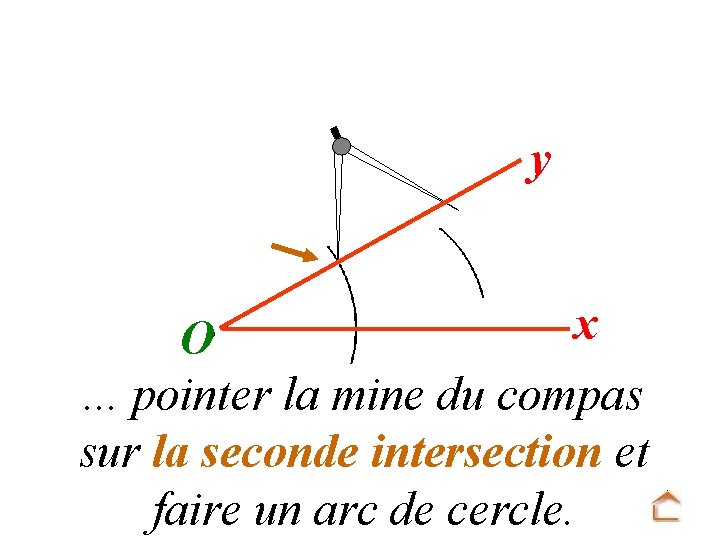
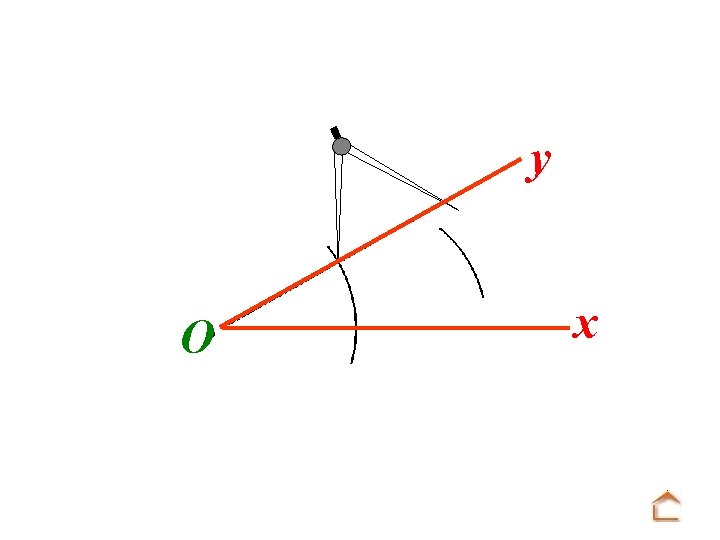
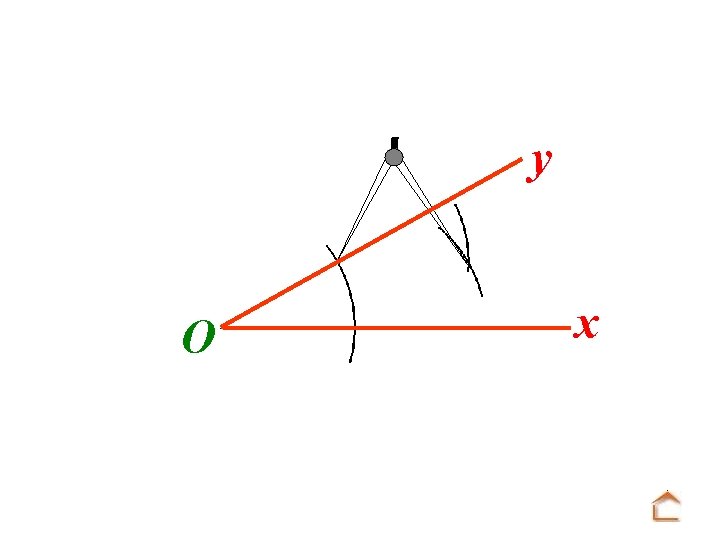
y x O. . . pointer la mine du compas sur la seconde intersection et faire un arc de cercle.

y O x

y O x

y O x

y O x

y O x

y O x

y O x

y O x

y O x

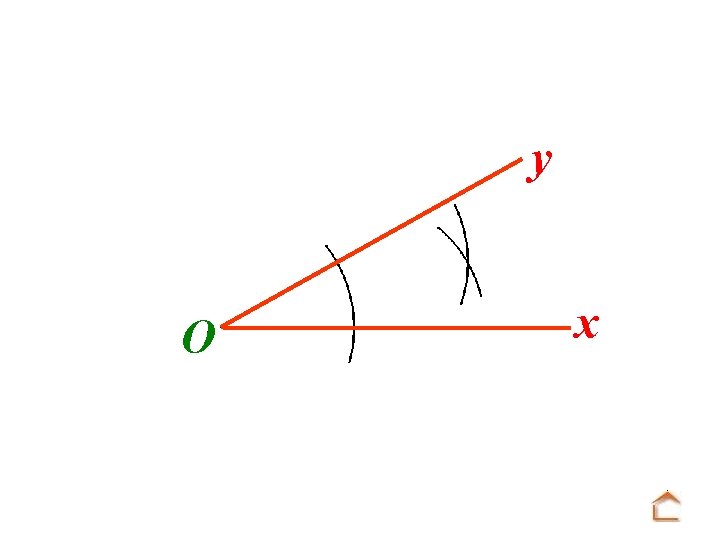
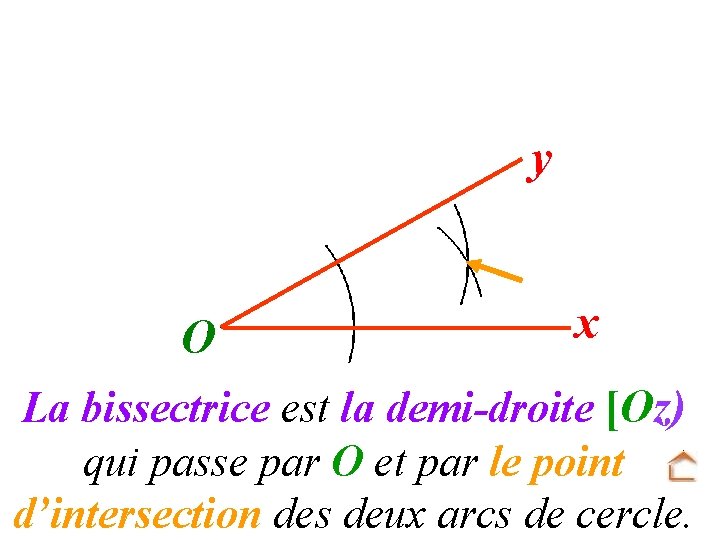
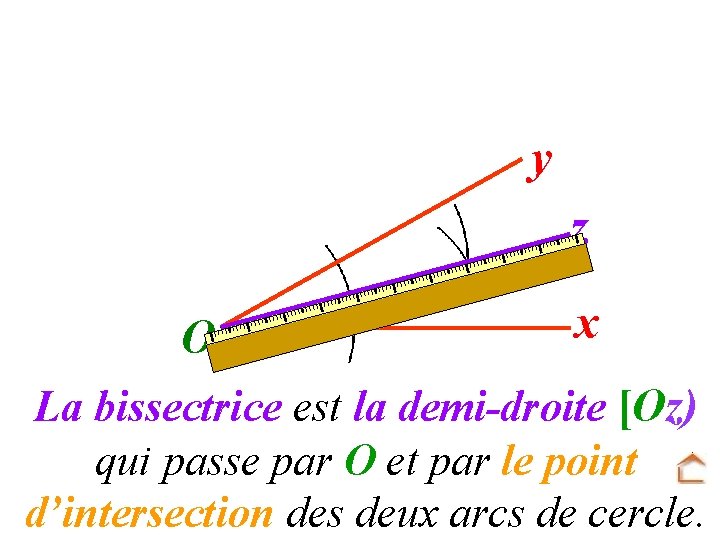
y O x La bissectrice est la demi-droite [Oz) qui passe par O et par le point d’intersection des deux arcs de cercle.

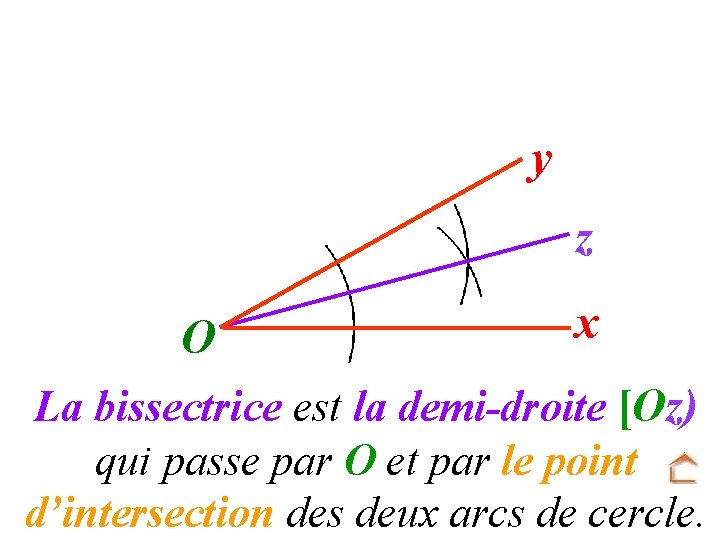
y z O x La bissectrice est la demi-droite [Oz) qui passe par O et par le point d’intersection des deux arcs de cercle.

y z O x La bissectrice est la demi-droite [Oz) qui passe par O et par le point d’intersection des deux arcs de cercle.

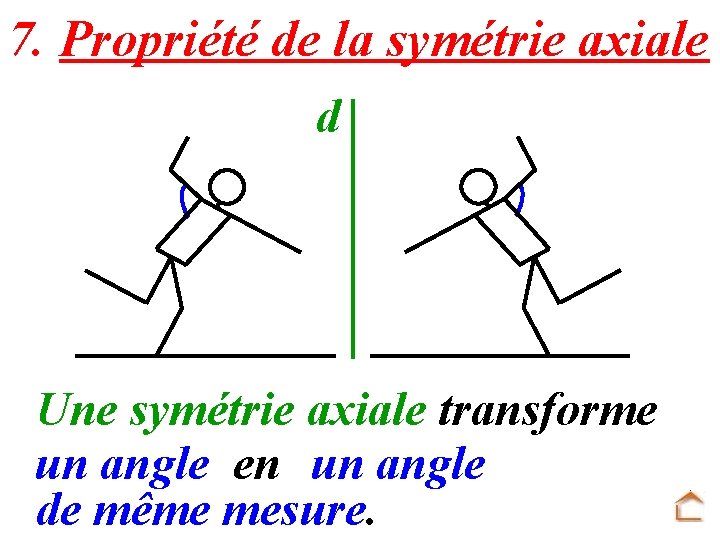
7. Propriété de la symétrie axiale d Une symétrie axiale transforme un angle en un angle de même mesure.

FIN