Les 3 Digitale Logica Overzicht Logische poorten Elementaire

Les 3: Digitale Logica

Overzicht • • • Logische poorten Elementaire elektronica Combinatorische schakelingen Sequentiële logica Technologie

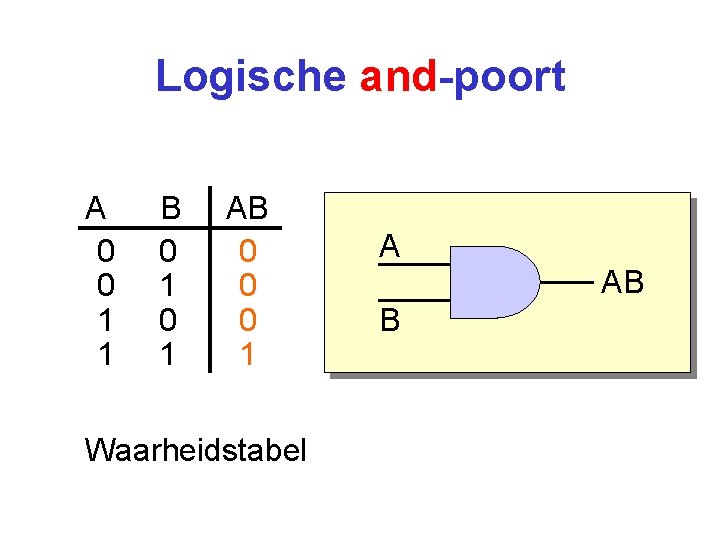
Logische and-poort A 0 0 1 1 B 0 1 AB 0 0 0 1 Waarheidstabel A AB B

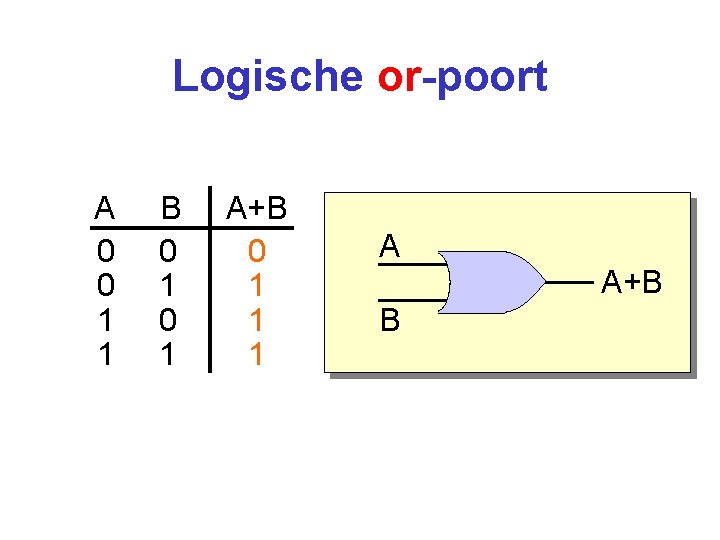
Logische or-poort A 0 0 1 1 B 0 1 A+B 0 1 1 1 A A+B B

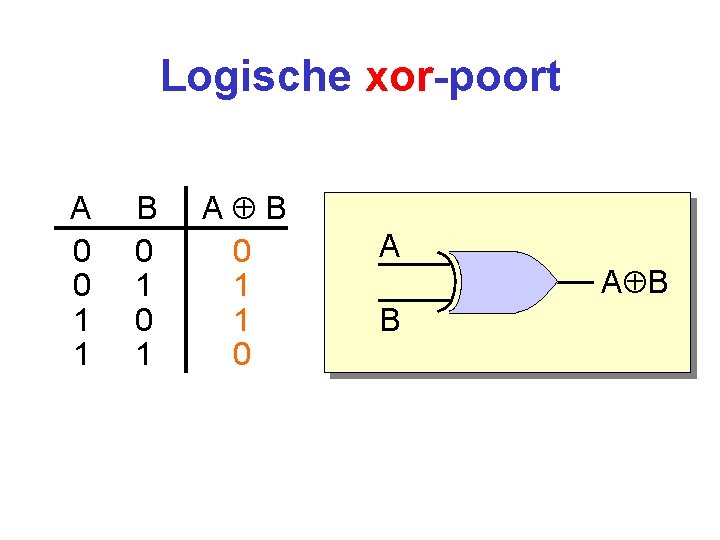
Logische xor-poort A 0 0 1 1 B 0 1 A B 0 1 1 0 A A B B

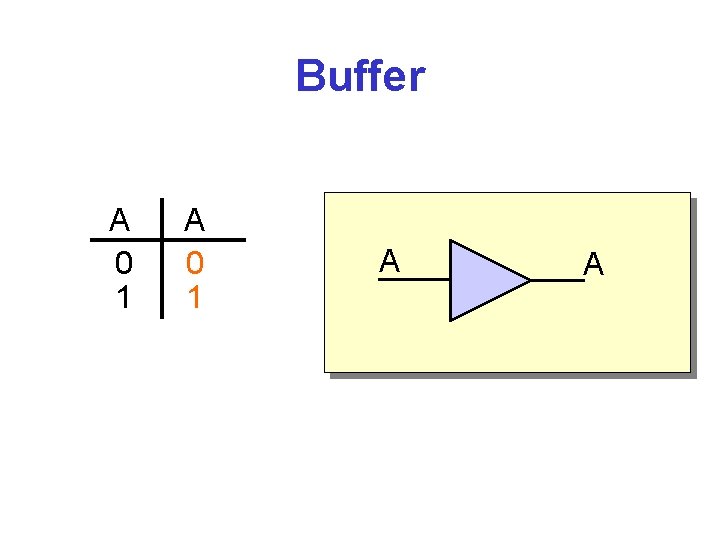
Buffer A 0 1 A A

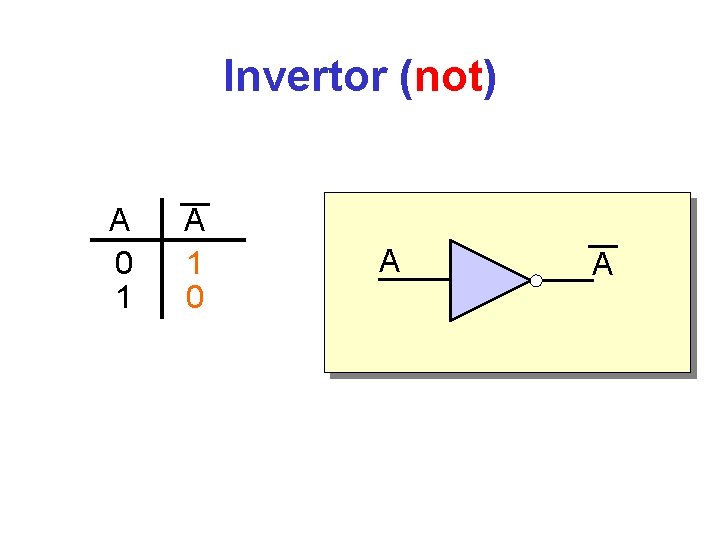
Invertor (not) A 0 1 A 1 0 A A

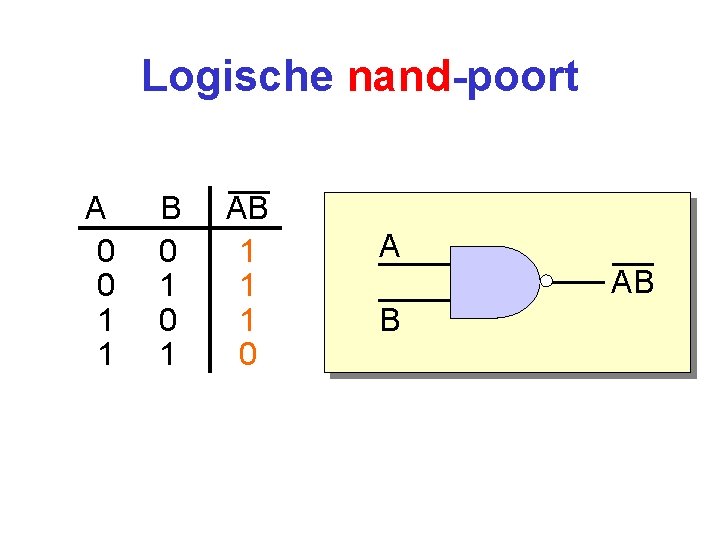
Logische nand-poort A 0 0 1 1 B 0 1 AB 1 1 1 0 A AB B

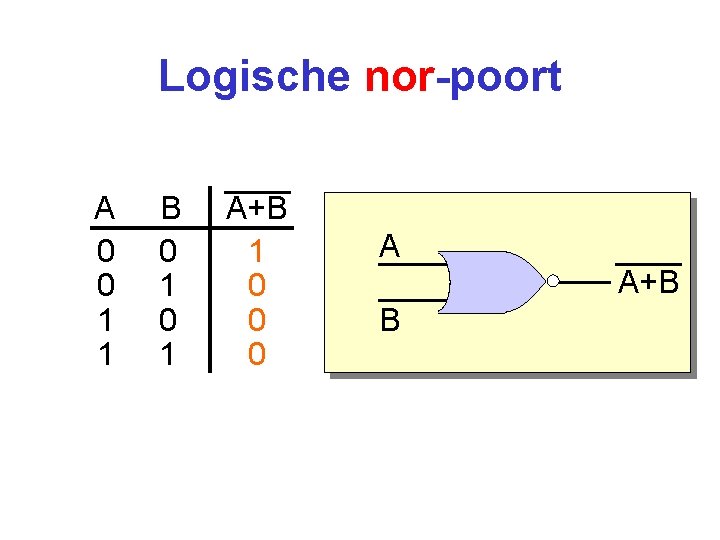
Logische nor-poort A 0 0 1 1 B 0 1 A+B 1 0 0 0 A A+B B

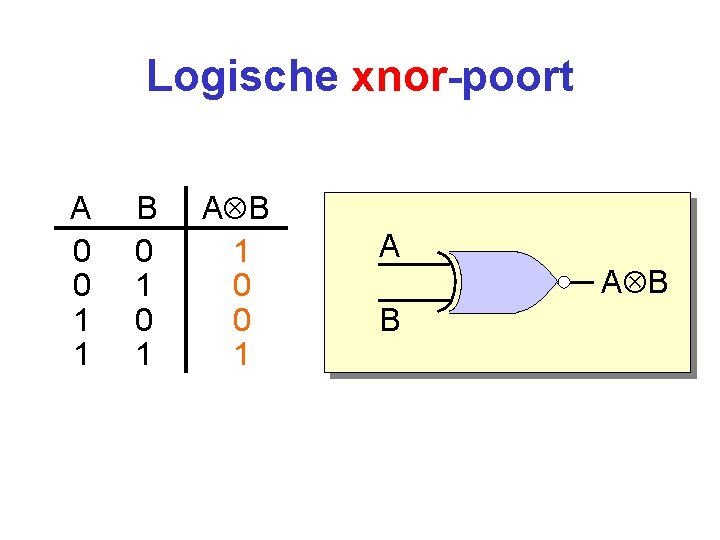
Logische xnor-poort A 0 0 1 1 B 0 1 A B 1 0 0 1 A A B B

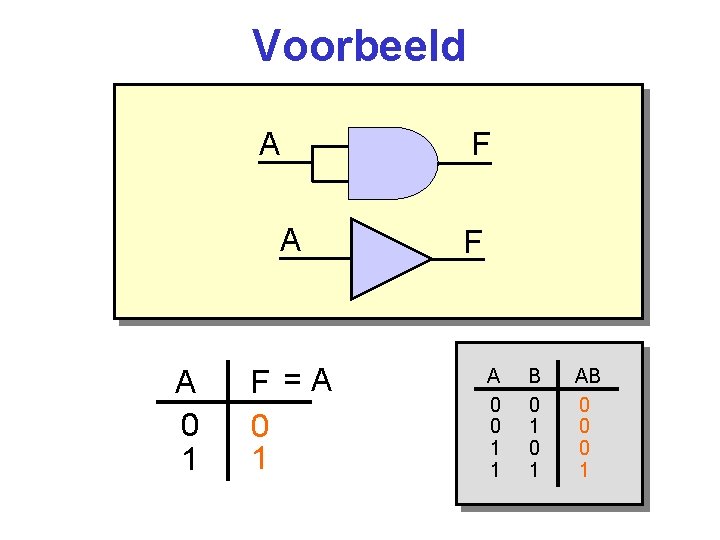
Voorbeeld A A A 0 1 F =A 0 1 F F A 0 0 1 1 B 0 1 AB 0 0 0 1

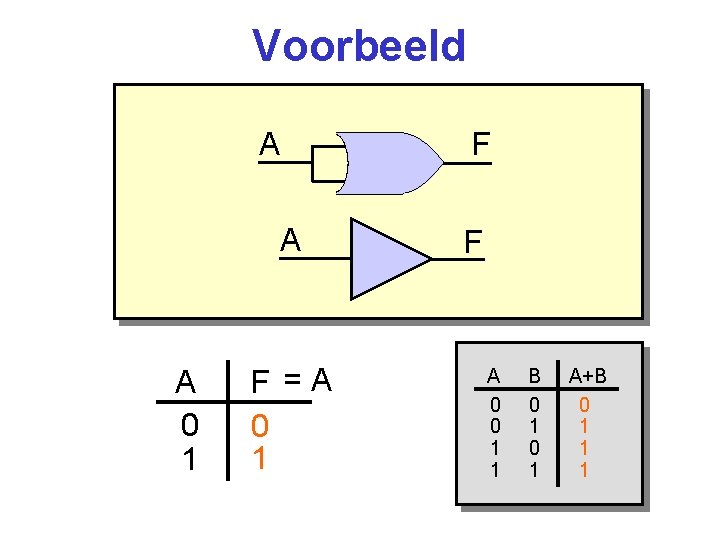
Voorbeeld A A A 0 1 F =A 0 1 F F A 0 0 1 1 B 0 1 A+B 0 1 1 1

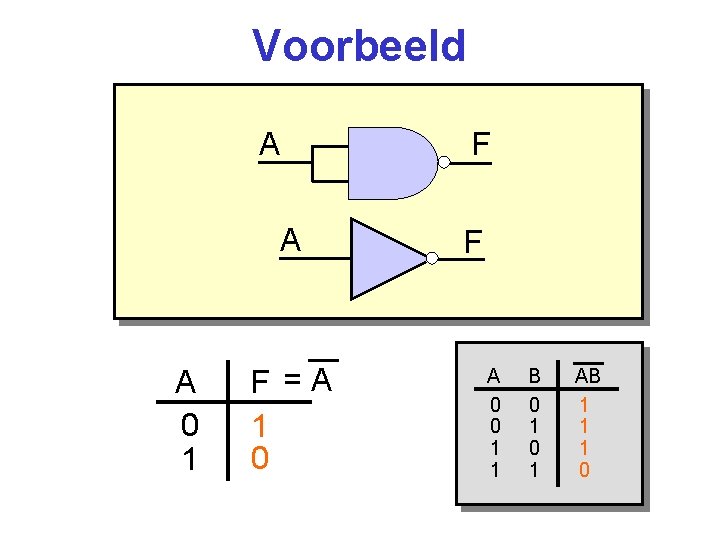
Voorbeeld A A A 0 1 F =A 1 0 F F A 0 0 1 1 B 0 1 AB 1 1 1 0

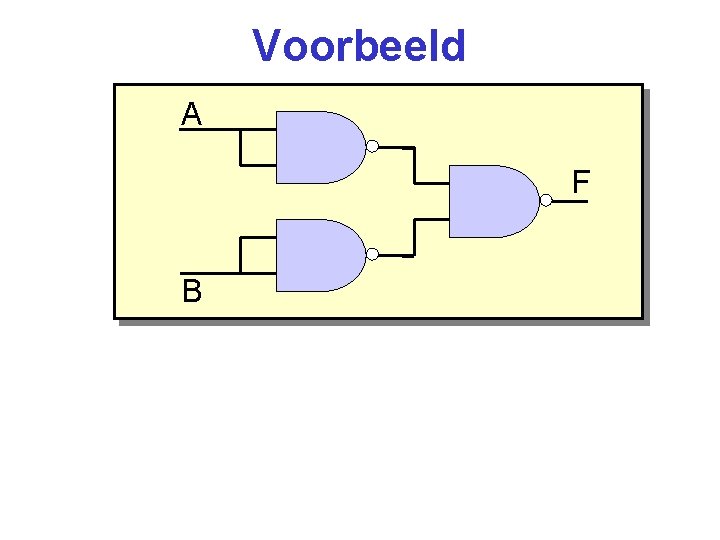
Voorbeeld A F B

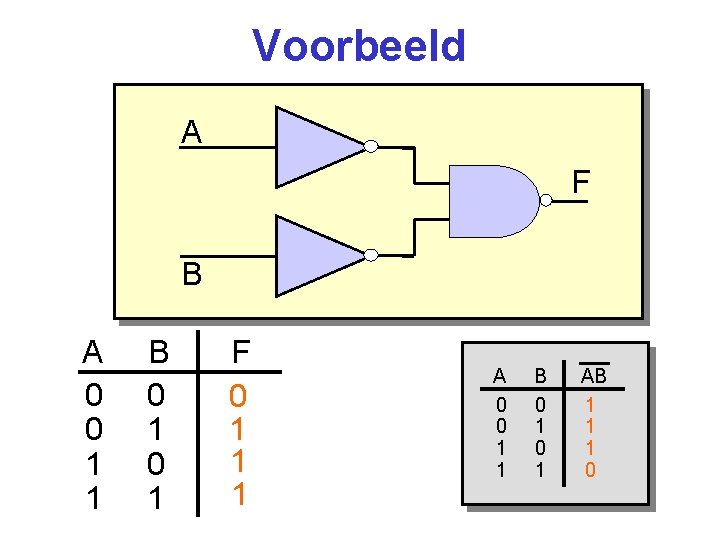
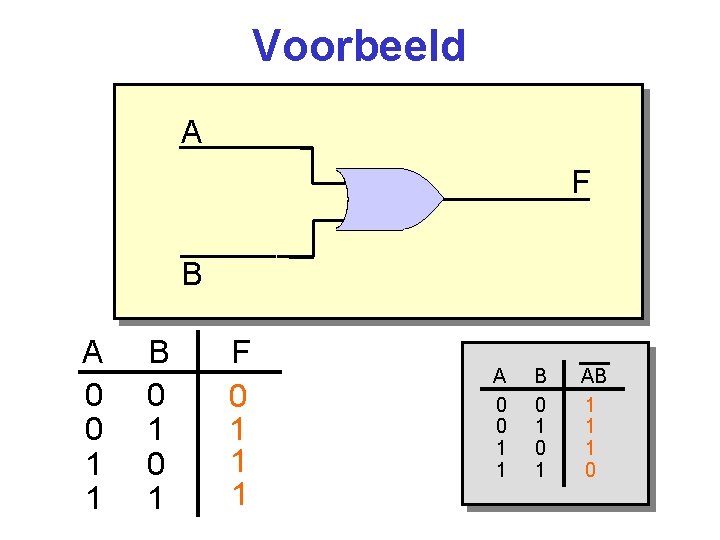
Voorbeeld A F B A 0 0 1 1 B 0 1 F 0 1 1 1 A 0 0 1 1 B 0 1 AB 1 1 1 0

Voorbeeld A F B A 0 0 1 1 B 0 1 F 0 1 1 1 A 0 0 1 1 B 0 1 AB 1 1 1 0

Voorbeeld A F B

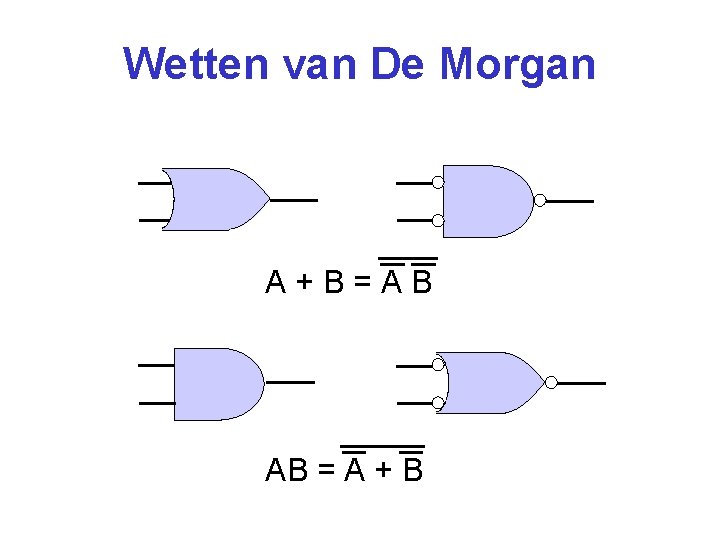
Wetten van De Morgan A+B=AB AB = A + B

Boolese algebra (1) Commutativiteit Distributiviteit Neutraal element Complement Nuleigenschap Idempotentie Associativiteit Dubbele negatie De Morgan Concensus Absorptie AB = BA A(B+C) = AB+AC 1 A = A AA = 0 0 A = 0 AA = A A(BC) = (AB)C A=A AB = A + B AB + AC + BC = AB + AC A(A+B) = A

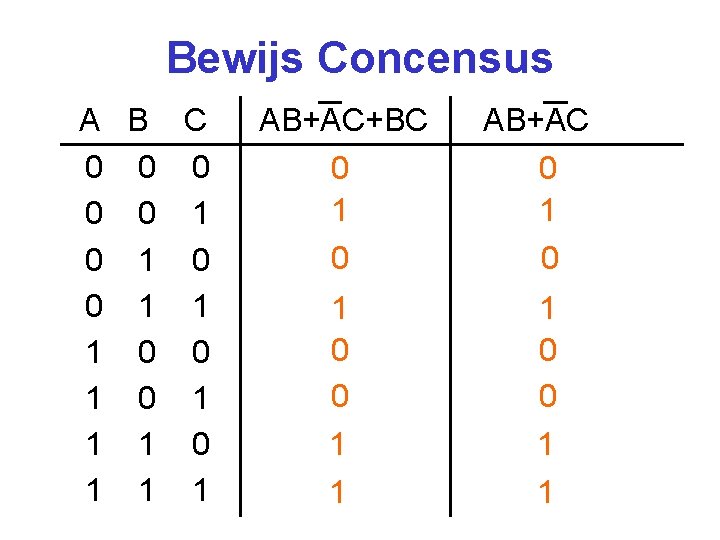
Bewijs Concensus A B C 0 0 0 1 1 1 0 0 1 1 1 AB+AC+BC 0 1 0 0 1 1 AB+AC 0 1 0 0 1 1

Boolese algebra (2) Commutativiteit A+B = B+A Distributiviteit A+(BC) = (A+B)(A+C) Neutraal element 0+A = A Complement A+A = 1 Eéneigenschap 1+A = 1 Idempotentie A+A = A Associativiteit A+(B+C) = (A+B)+C Dubbele negatie De Morgan A+B = AB Concensus (A+B)(A+C)(B+C) = (A+B)(A+C) Absorptie A+(AB) = A

Overzicht • • • Logische poorten Elementaire elektronica Combinatorische schakelingen Sequentiële logica Technologie

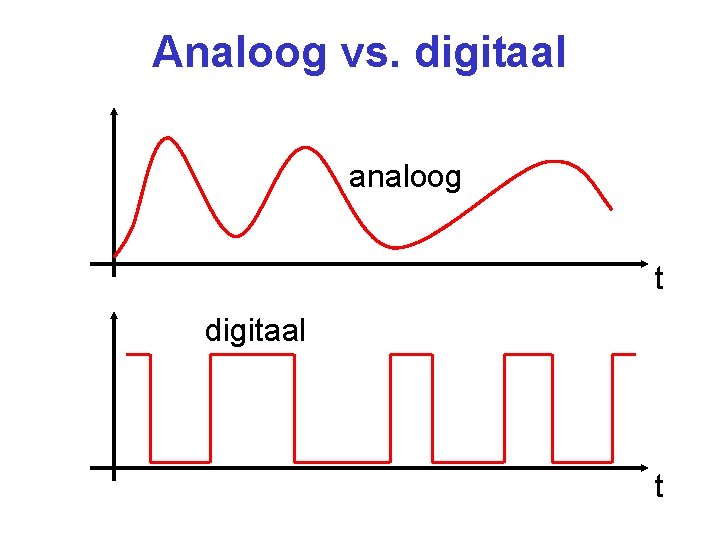
Analoog vs. digitaal analoog t digitaal t

Elementaire elektrische grootheden Eenheid van stroom: Ampere (A) Eenheid van spanning: Volt (V) Eenheid van vermogen: Watt (W) Eenheid van weerstand: Ohm ( )

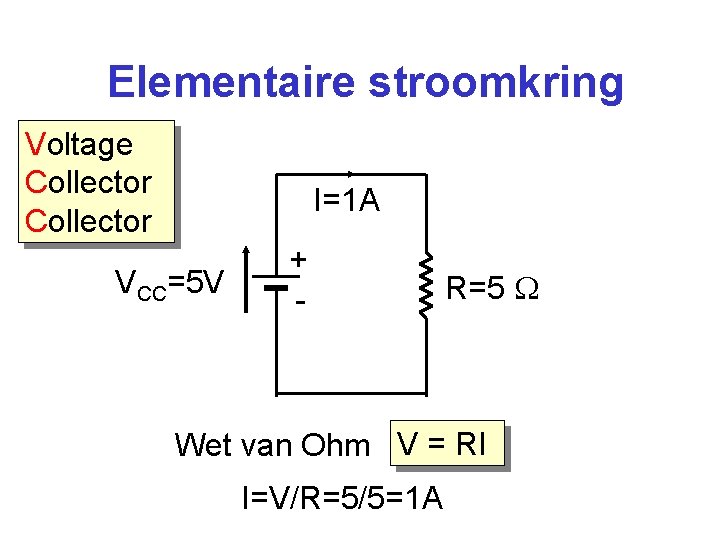
Elementaire stroomkring Voltage Collector I=1 A VCC=5 V + - R=5 Wet van Ohm V = RI I=V/R=5/5=1 A

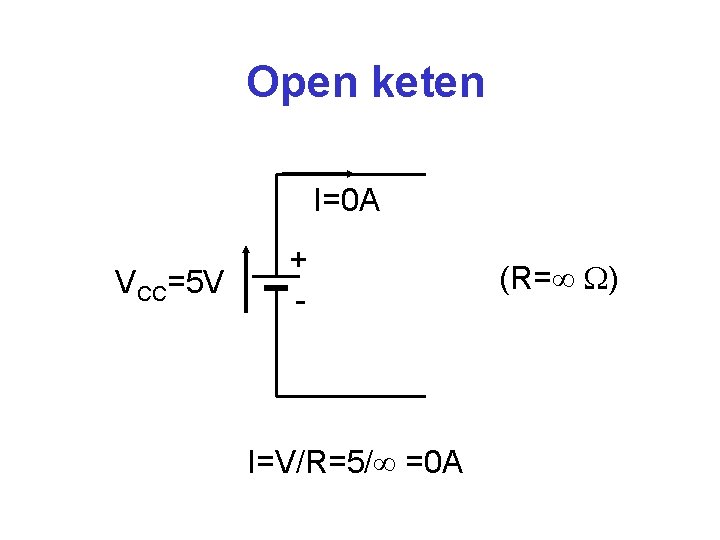
Open keten I=0 A VCC=5 V + - I=V/R=5/ =0 A (R= )

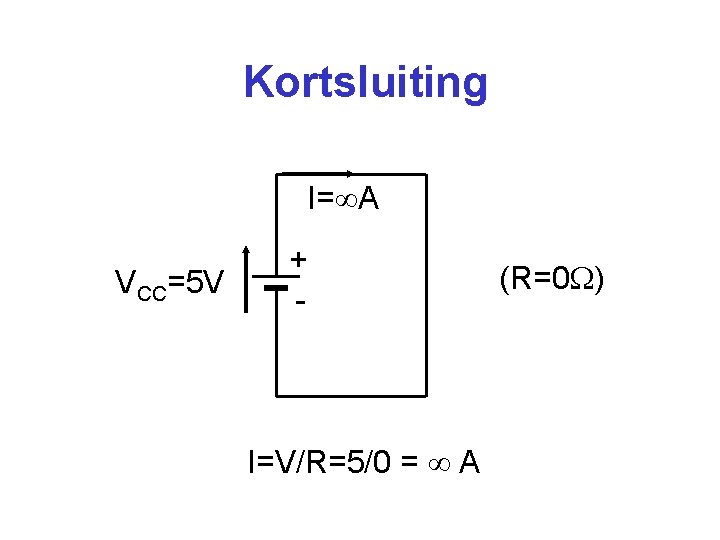
Kortsluiting I= A VCC=5 V + - I=V/R=5/0 = A (R=0 )

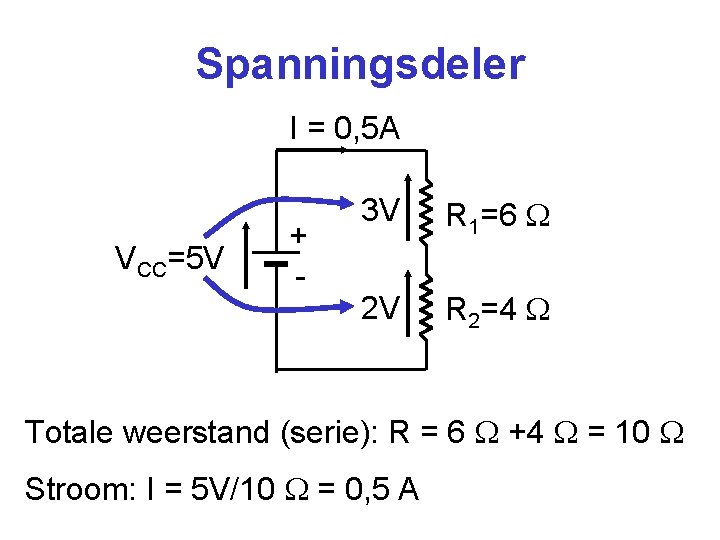
Spanningsdeler I = 0, 5 A VCC=5 V + - 3 V R 1=6 2 V R 2=4 Totale weerstand (serie): R = 6 +4 = 10 Stroom: I = 5 V/10 = 0, 5 A

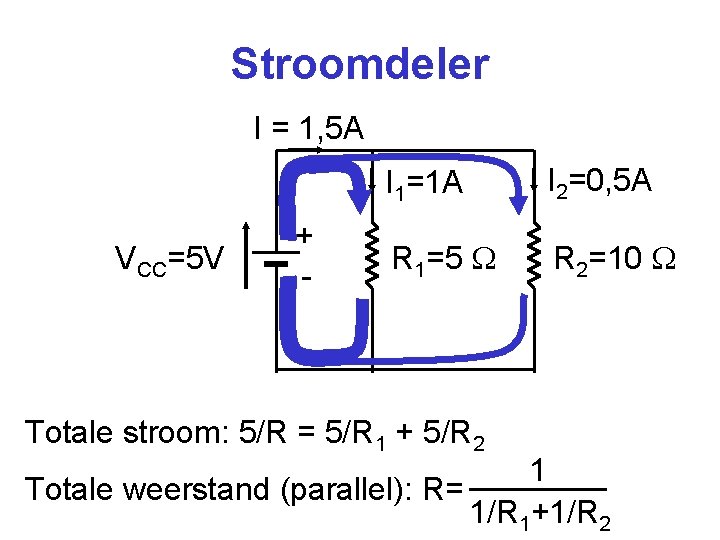
Stroomdeler I = 1, 5 A VCC=5 V + - I 1=1 A I 2=0, 5 A R 1=5 R 2=10 Totale stroom: 5/R = 5/R 1 + 5/R 2 1 Totale weerstand (parallel): R= 1/R 1+1/R 2

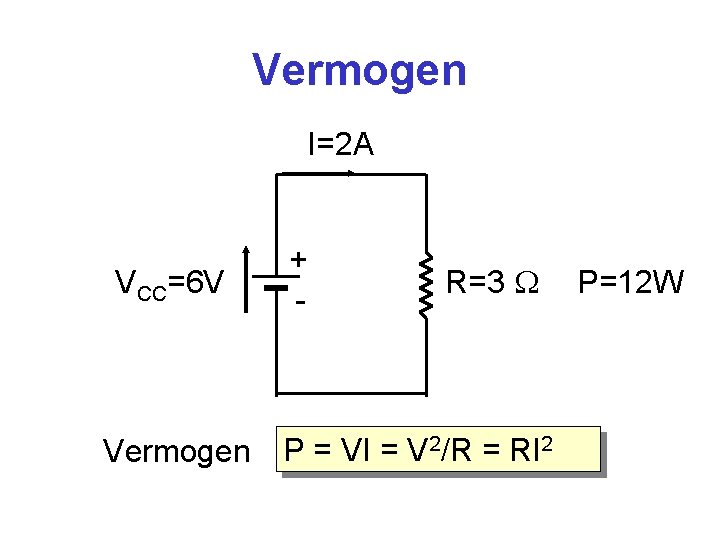
Vermogen I=2 A VCC=6 V Vermogen + - R=3 P = VI = V 2/R = RI 2 P=12 W

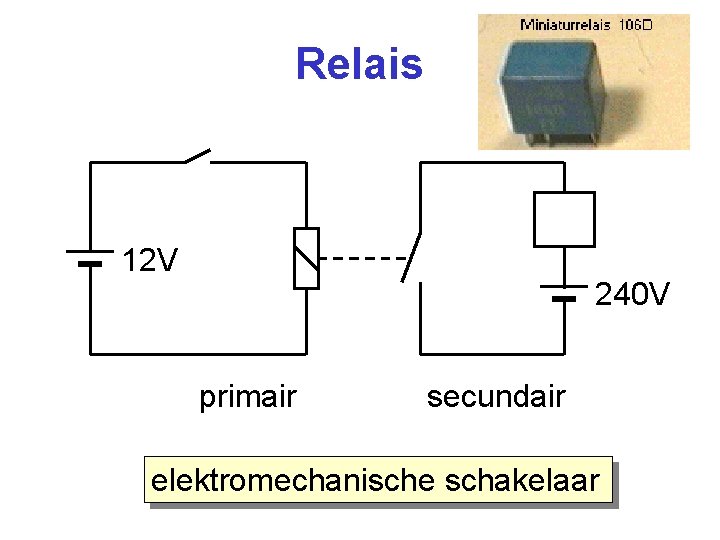
Relais 12 V 240 V primair secundair elektromechanische schakelaar

Transistor (transfer resistor) Bardeen, Shockley, and Brattain (1947), Bell Labs Nobelprijs: 1956 collector basis emittor halfgeleiderschakelaar

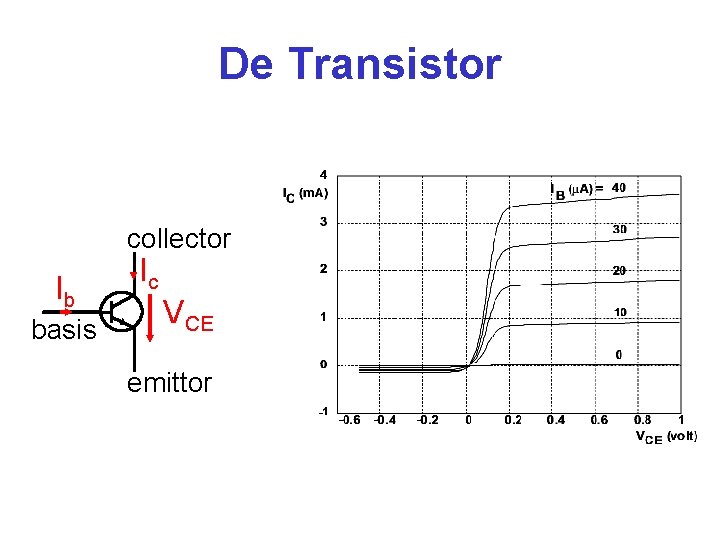
De Transistor collector Ib basis Ic VCE emittor

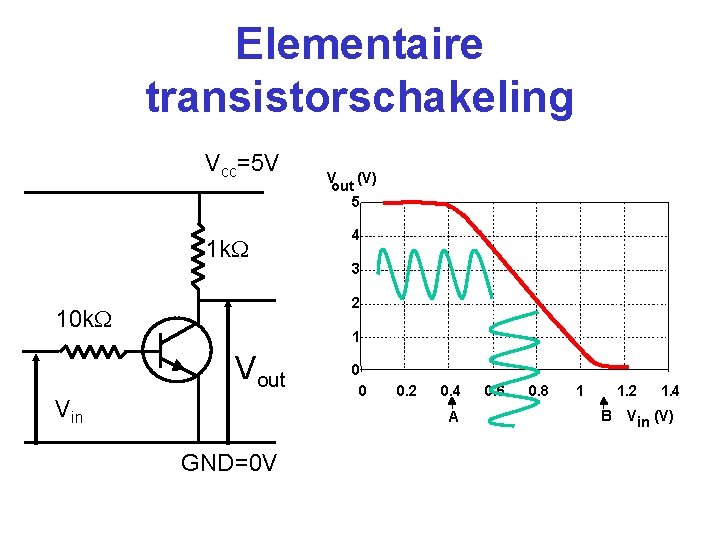
Elementaire transistorschakeling Vcc=5 V 1 k V (V) out 5 4 3 2 10 k 1 Vout Vin 0 0 0. 2 0. 4 A GND=0 V 0. 6 0. 8 1 1. 2 1. 4 B V in (V)

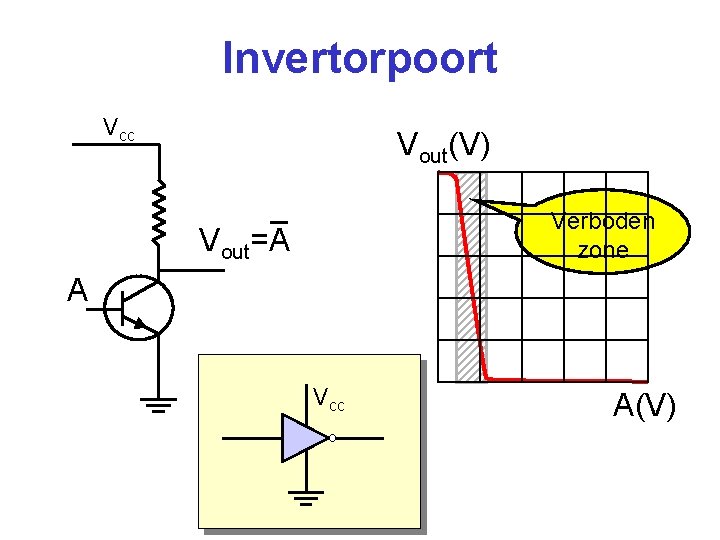
Invertorpoort Vcc Vout(V) Verboden zone Vout=A A Vcc A(V)

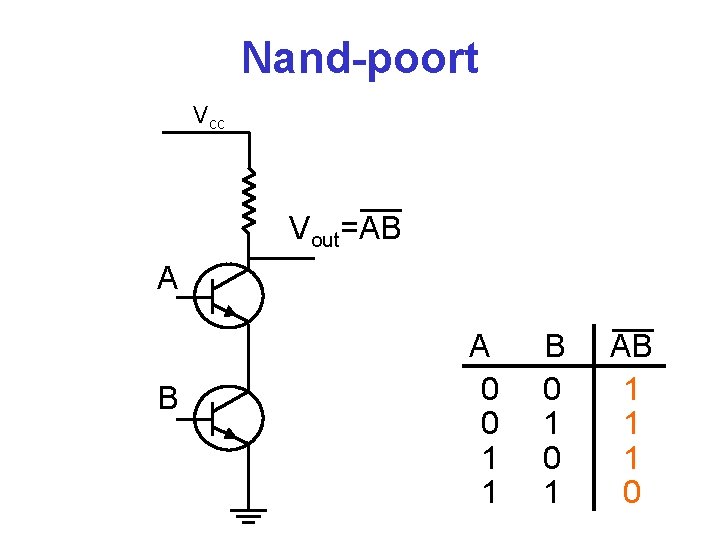
Nand-poort Vcc Vout=AB A 0 0 1 1 B 0 1 AB 1 1 1 0

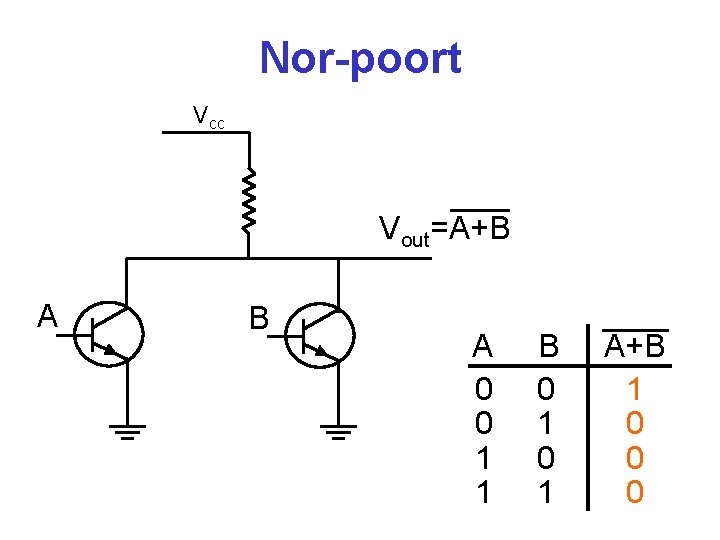
Nor-poort Vcc Vout=A+B A 0 0 1 1 B 0 1 A+B 1 0 0 0

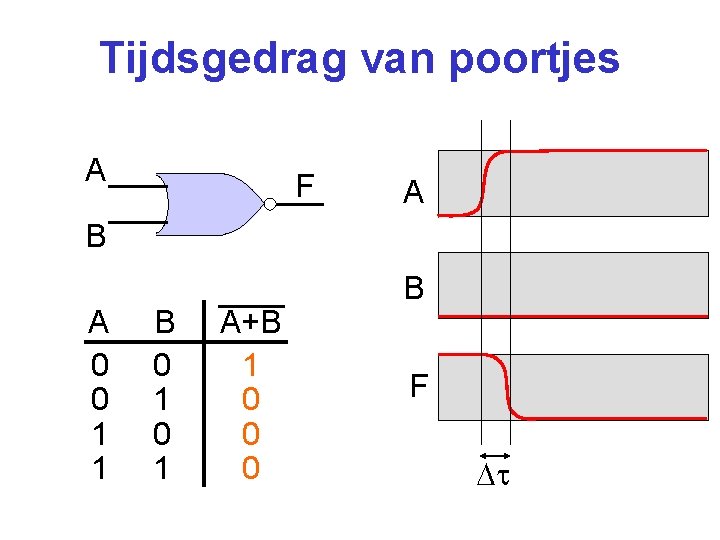
Tijdsgedrag van poortjes A F A B A 0 0 1 1 B 0 1 A+B 1 0 0 0 B F

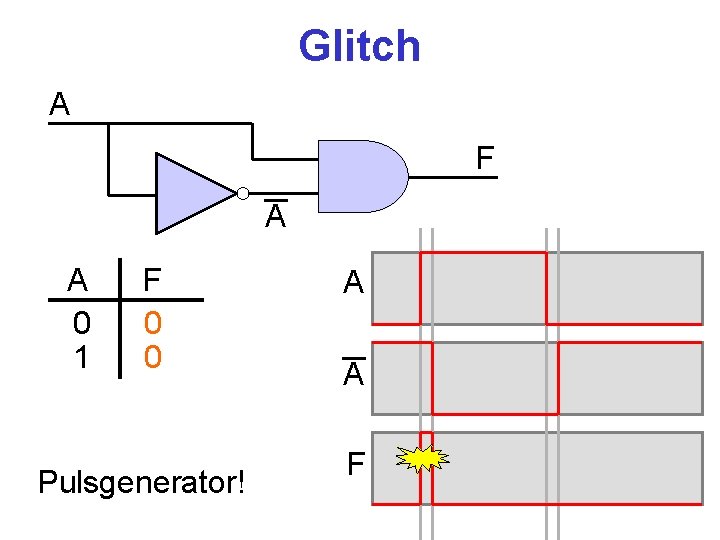
Glitch A F A A 0 1 F 0 0 Pulsgenerator! A A F

Tri-state F A C C 0 0 1 1 F A C A 0 1 F 0 1 “elektrisch afkoppelen” C 0 0 1 1 A 0 1 F 0 1

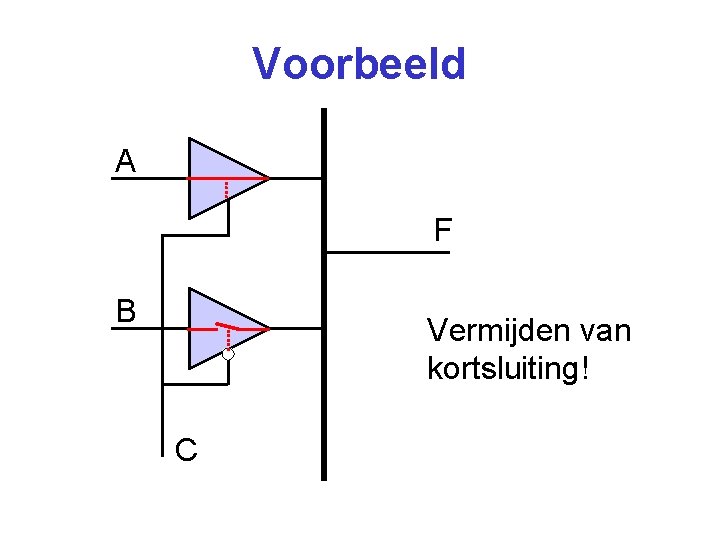
Voorbeeld A F B Vermijden van kortsluiting! C

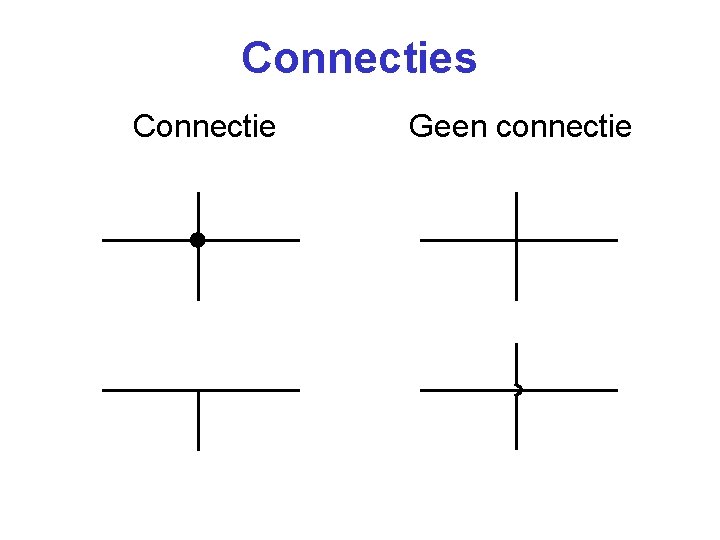
Connecties Connectie Geen connectie

Overzicht • • • Logische poorten Elementaire elektronica Combinatorische schakelingen Sequentiële logica Technologie

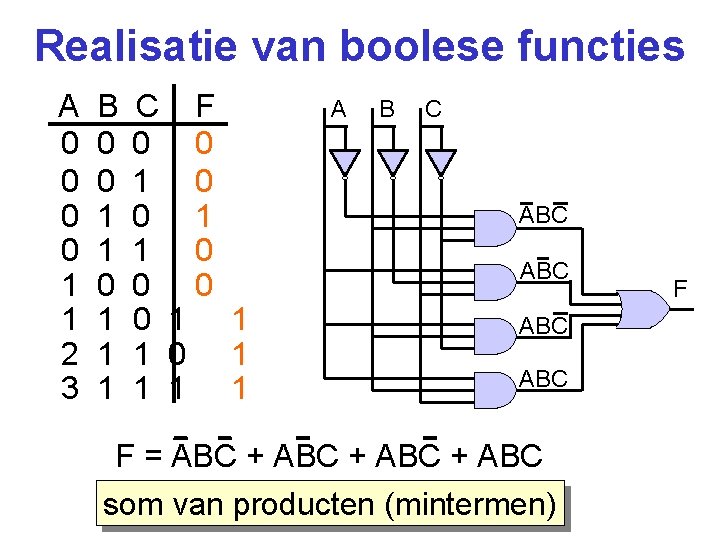
Realisatie van boolese functies A 0 0 1 1 2 3 B 0 0 1 1 1 C F 0 0 1 1 1 0 1 1 A B C ABC ABC F = ABC + ABC som van producten (mintermen) F

Realisatie van boolese functies A 0 0 1 1 2 3 B 0 0 1 1 1 C F F’ = ABC + ABC 0 0 1 0 F = ABC + ABC 0 1 De Morgan 1 0 0 1 1 F = (ABC)(ABC) 1 0 1 1 De Morgan & dubbele negatie F = (A+B+C)(A+B+C) product van sommen (maxtermen)

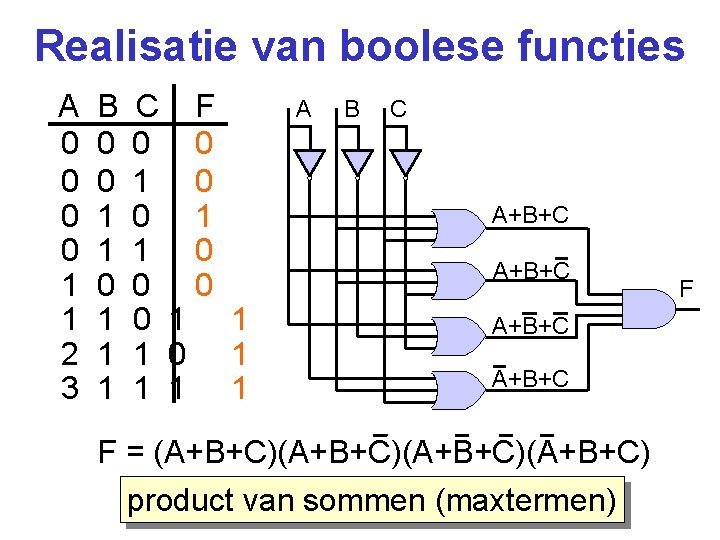
Realisatie van boolese functies A 0 0 1 1 2 3 B 0 0 1 1 1 C F 0 0 1 1 1 0 1 1 A B C A+B+C F = (A+B+C)(A+B+C) product van sommen (maxtermen) F

Minimalisatie • Een realisatie als som van producten of product van sommen is vaak niet optimaal. F = ABC + ABC F = ABC + BAC + ABC + BAC F = ABC + BAC F = (A+A)BC + (B+B)AC F = 1 BC + 1 AC F = BC + AC

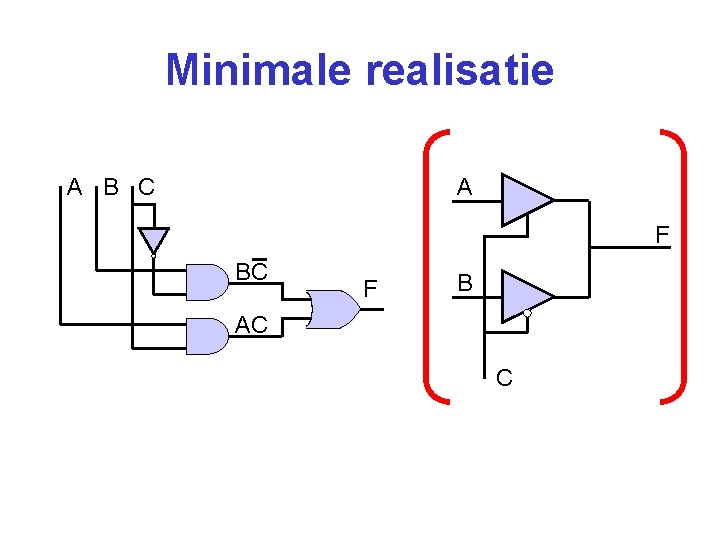
Minimale realisatie A B C A F BC F B AC C

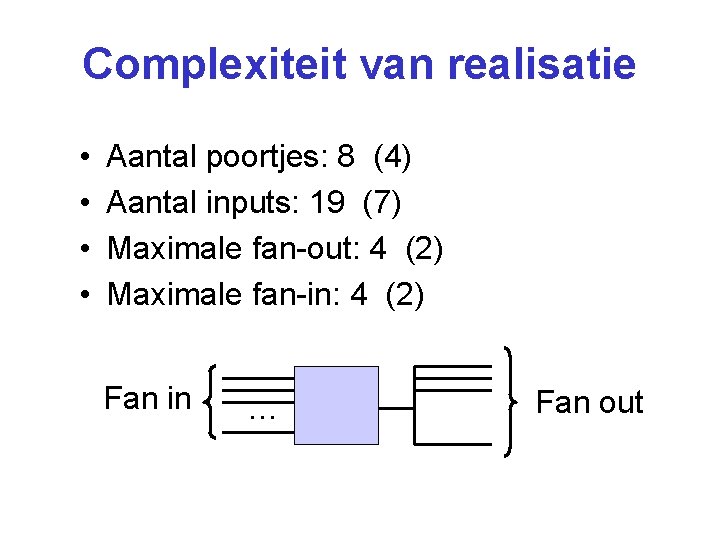
Complexiteit van realisatie • • Aantal poortjes: 8 (4) Aantal inputs: 19 (7) Maximale fan-out: 4 (2) Maximale fan-in: 4 (2) Fan in … Fan out

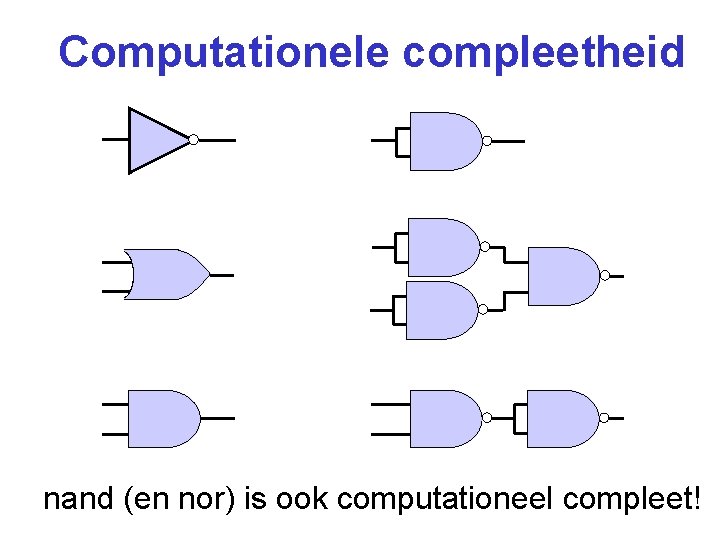
Computationele compleetheid Een willekeurige combinatorische functie kan gerealiseerd worden met slechts 3 poortjes: and, or, not.

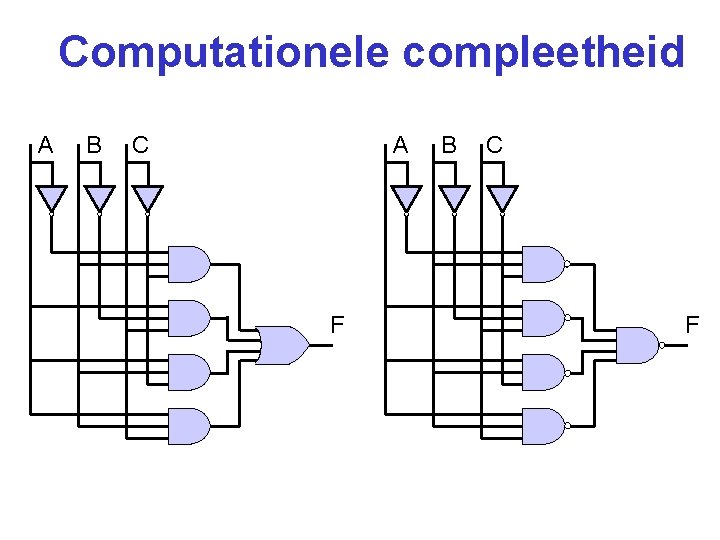
Computationele compleetheid nand (en nor) is ook computationeel compleet!

Computationele compleetheid A B C A F B C F

Digitale componenten • • Multiplexer Demultiplexer Decoder Prioriteitsencoder

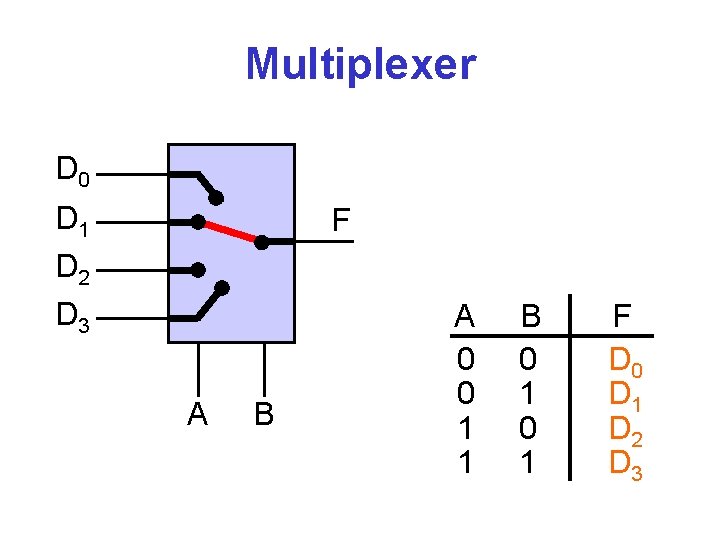
Multiplexer D 0 D 1 D 2 D 3 F A B A 0 0 1 1 B 0 1 F D 0 D 1 D 2 D 3

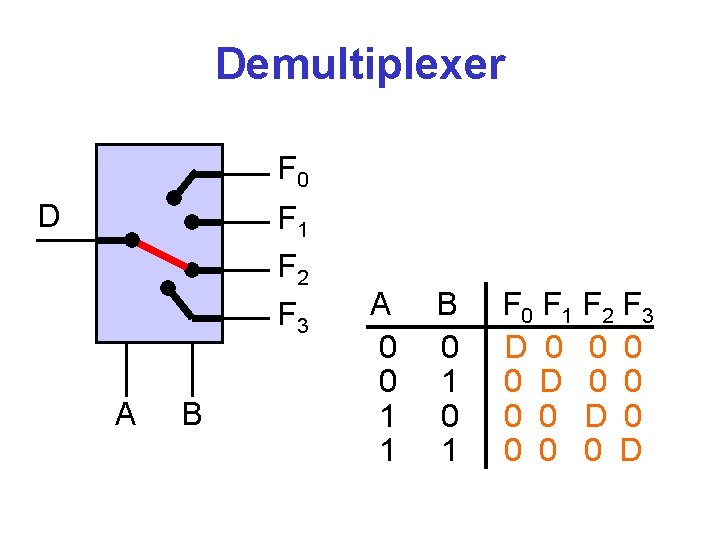
Demultiplexer F 0 D F 1 F 2 F 3 A B A 0 0 1 1 B 0 1 F 0 F 1 F 2 F 3 D 0 0 0 0 D

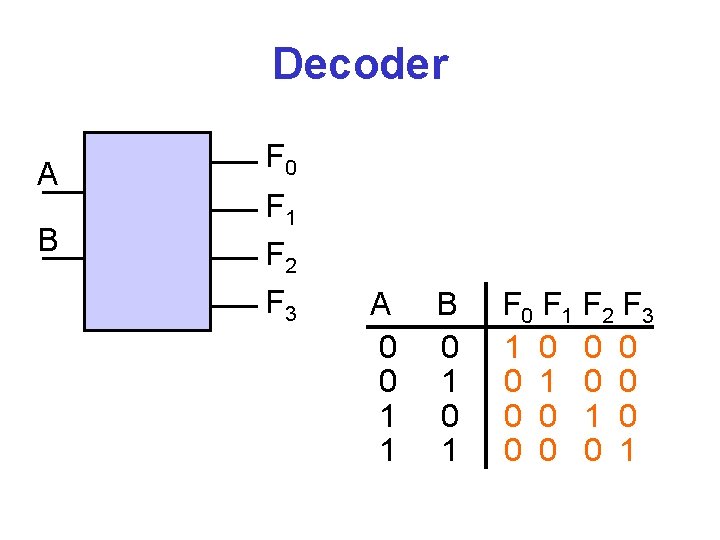
Decoder A B F 0 F 1 F 2 F 3 A 0 0 1 1 B 0 1 F 0 F 1 F 2 F 3 1 0 0 0 0 1

Prioriteitsencoder A 0 A 1 A 2 A 3 F 0 F 1 A 0 A 1 A 2 A 3 0 0 0 0 1 1 1. 0 1 0 2. 0 1 0 3. 0 1 1 4. 0 1 1 5. 1 0 0 6. 1 0 0 7. 1 0 1 8. 1 0 1 9. 1 1 0 10. 01 1 0 11. 01 1 1 12. 1 1 1 F 0 F 1 0 0 1 1 1 0 0 0 1 0 0 0 1 0 1 1 0 0 0

Overzicht • • • Logische poorten Elementaire elektronica Combinatorische schakelingen Sequentiële logica Technologie

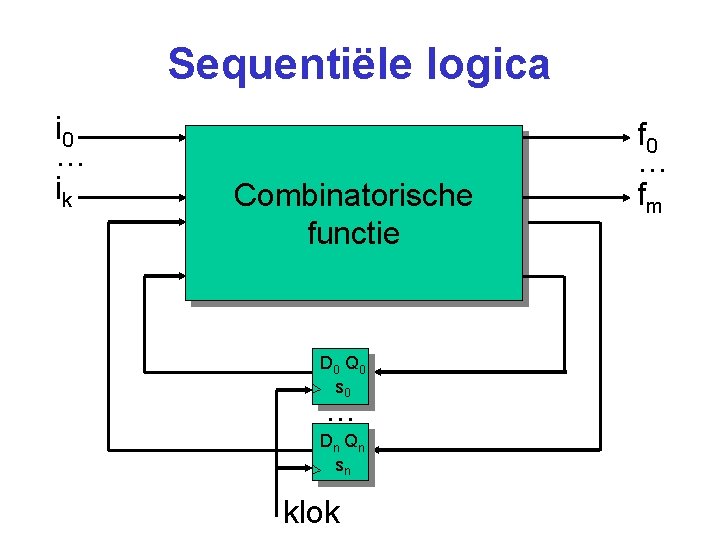
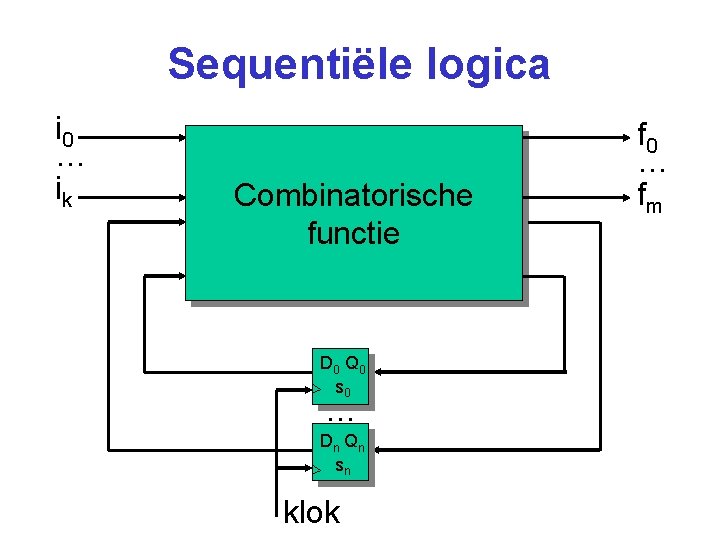
Sequentiële logica i 0 … ik Combinatorische functie D 0 Q 0 s 0 … Dn Q n sn klok f 0 … fm

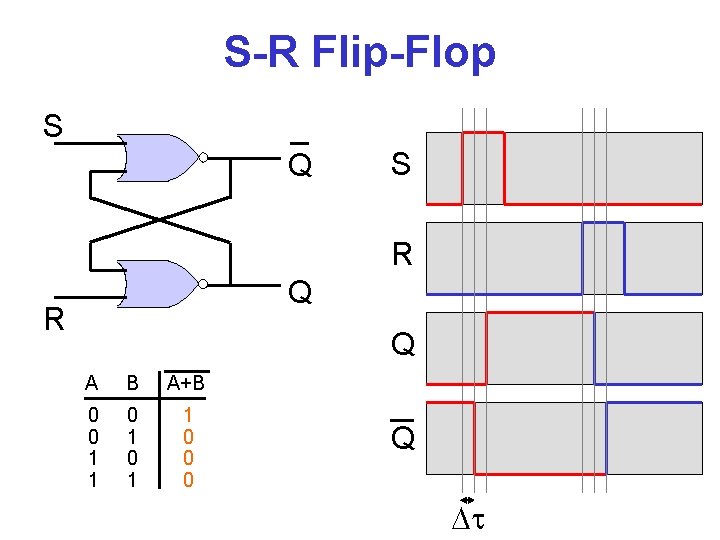
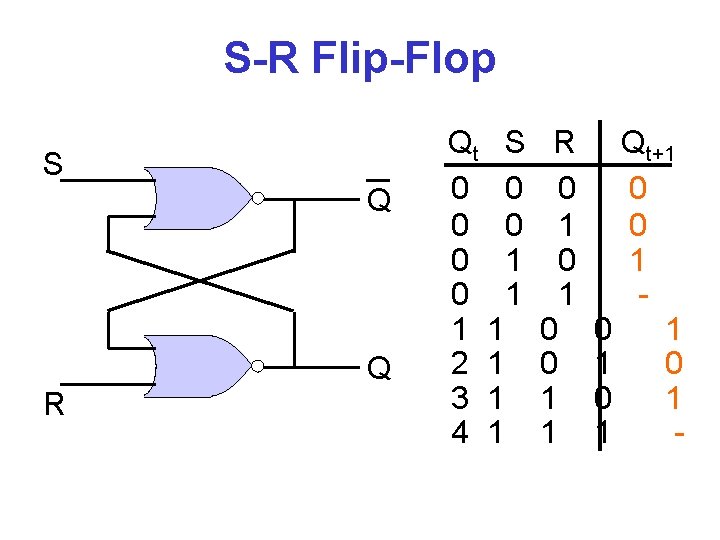
S-R Flip-Flop S Q S R Q A B A+B 0 0 1 1 0 0 0 Q

S-R Flip-Flop S Q Q R Qt S 0 0 0 1 1 1 2 1 3 1 4 1 R 0 1 0 0 1 1 Qt+1 0 0 1 1 -

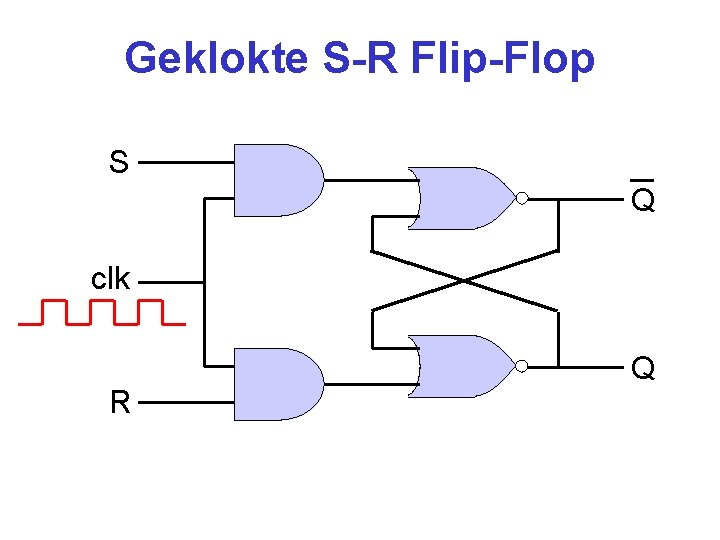
Geklokte S-R Flip-Flop S Q clk R Q

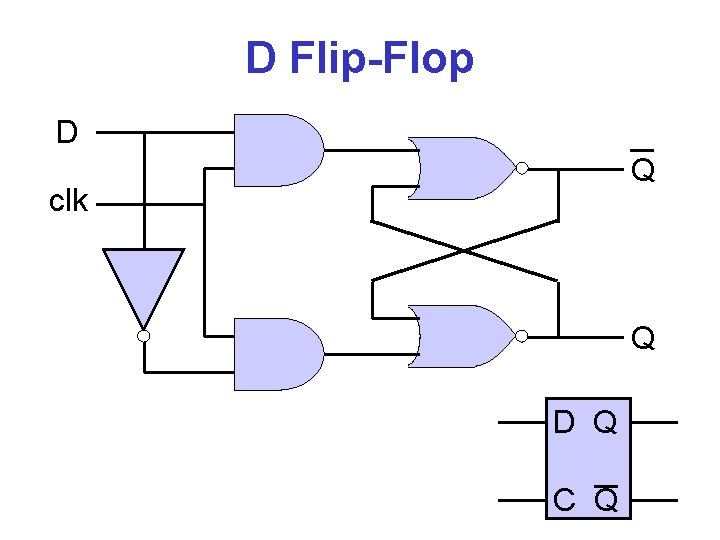
D Flip-Flop D Q clk Q D Q C Q

Sequentiële logica i 0 … ik Combinatorische functie D 0 Q 0 s 0 … Dn Q n sn klok f 0 … fm

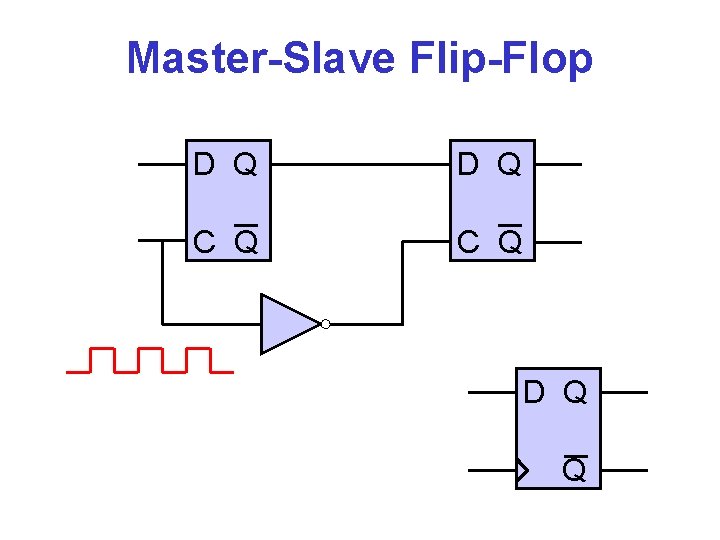
Master-Slave Flip-Flop D Q C Q D Q Q

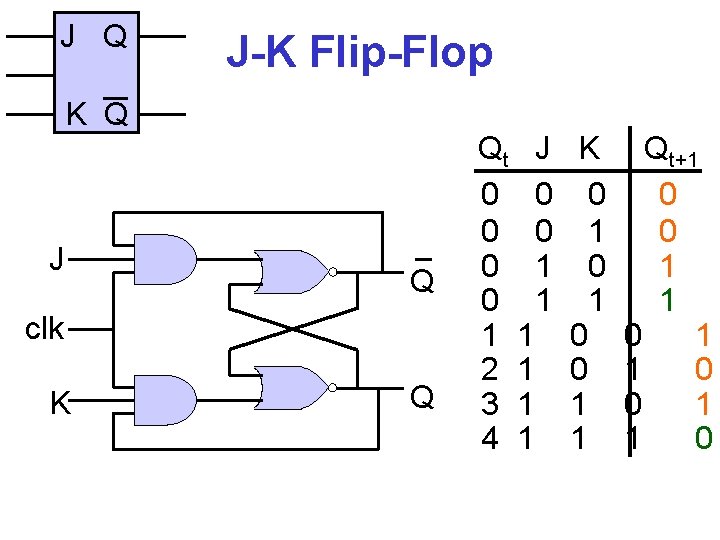
J Q J-K Flip-Flop K Q J Q clk K Q Qt J 0 0 0 1 1 1 2 1 3 1 4 1 K 0 1 0 0 1 1 Qt+1 0 0 1 1 0

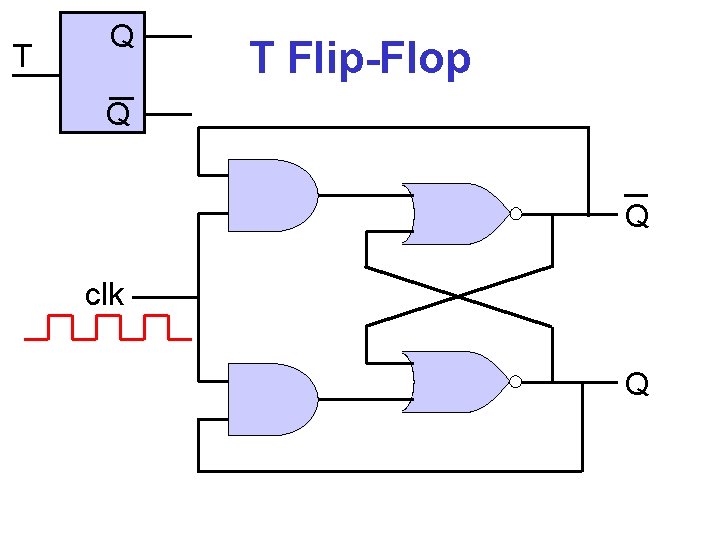
T Q T Flip-Flop Q 1 Q clk 1 Q

Overzicht • • • Logische poorten Elementaire elektronica Combinatorische schakelingen Sequentiële logica Technologie

Technologie: wafer

Technologie: die

Technologie: transistor

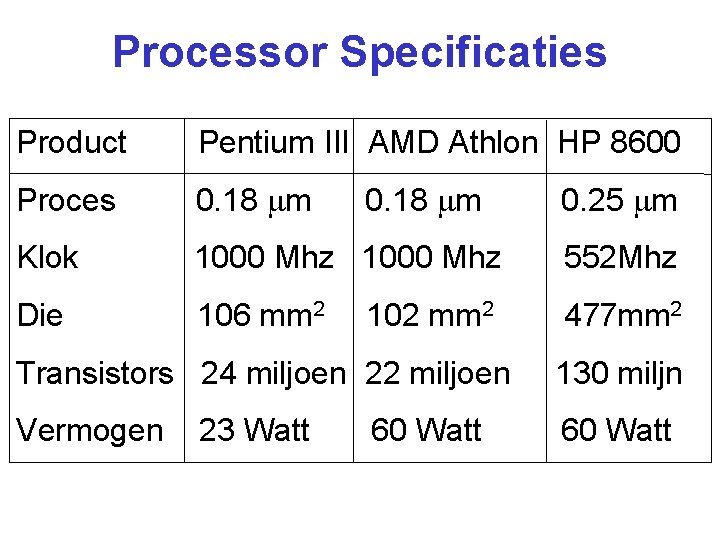
Processor Specificaties Product Pentium III AMD Athlon HP 8600 Proces 0. 18 m Klok 1000 Mhz 552 Mhz Die 106 mm 2 477 mm 2 0. 18 m 102 mm 2 0. 25 m Transistors 24 miljoen 22 miljoen 130 miljn Vermogen 60 Watt 23 Watt 60 Watt