Lenses 2 CALCULATIONS USING THE LENS FORMULA Calculate

Lenses 2

CALCULATIONS USING THE LENS FORMULA Calculate the distance of the image to the converging lens in the following situations object distance /cm Focal length /cm a 30. 0 40. 0 b 25. 0 20. 0 c 50. 0 20. 0 d 40. 0 In each case say whether the image is real or virtual

Solved Example object distanc e /cm Focal length /cm Image dist ance cm a 30. 0 40. 0 -120 (virtual) b 25. 0 20. 0 100 (real) c 50. 0 20. 0 33. 3 cm (real) d 40. 0 No image (rays emerge parallel) V= -120 cm The image is 120 cm from the lens and it is virtual (- sign)

The power of a lens By definition the power of a lens is the reciprocal of its focal length in metres: Lens power The unit of lens power is m These units are often referred to as dioptres (D). -1. Therefore a lens with a power of 3 D has a focal length of 1/3 m The dioptre is not a standard SI unit This of course also means that the power of a lens is given by:

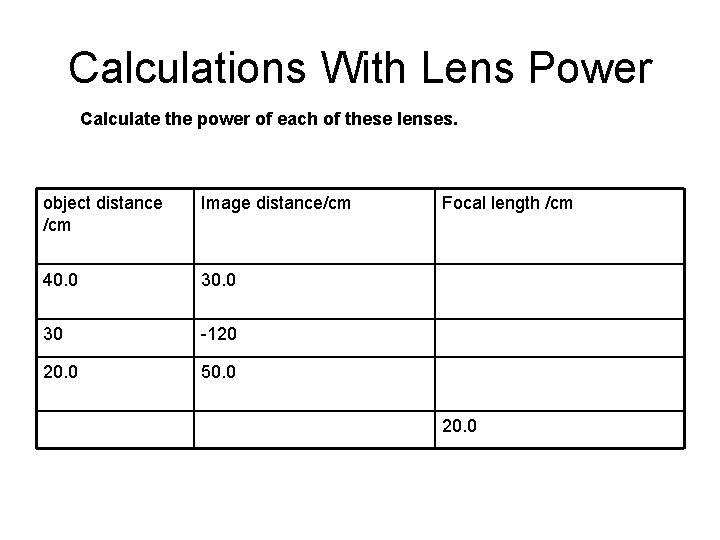
Calculations With Lens Power Calculate the power of each of these lenses. object distance /cm Image distance/cm 40. 0 30 -120 20. 0 50. 0 Focal length /cm 20. 0

Determination Of The Focal Length Of A Converging Lens The distant object method: To make a rough estimate of the focal length of a convex lens. Produce a sharply illuminated image of a distant object (e. g. a distant window). To a rough approximation the rays of light from the object will be arriving parallel at the screen and therefore the distance between the lens and the screen is approximately the focal length of the lens.

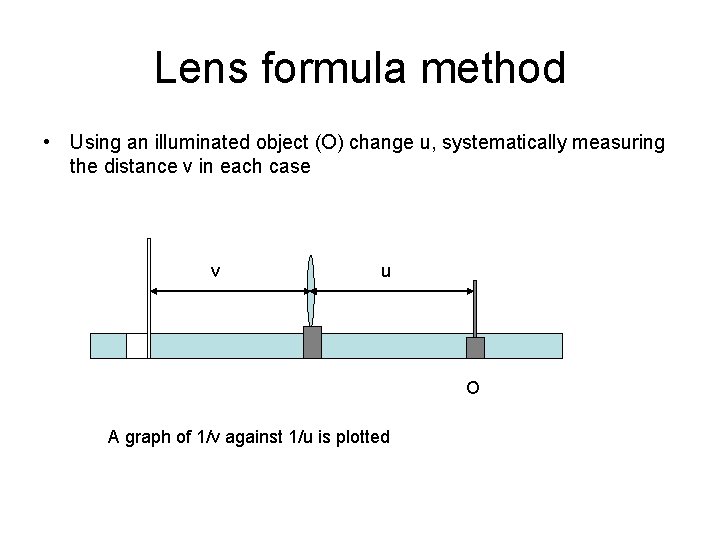
Lens formula method • Using an illuminated object (O) change u, systematically measuring the distance v in each case v u O A graph of 1/v against 1/u is plotted

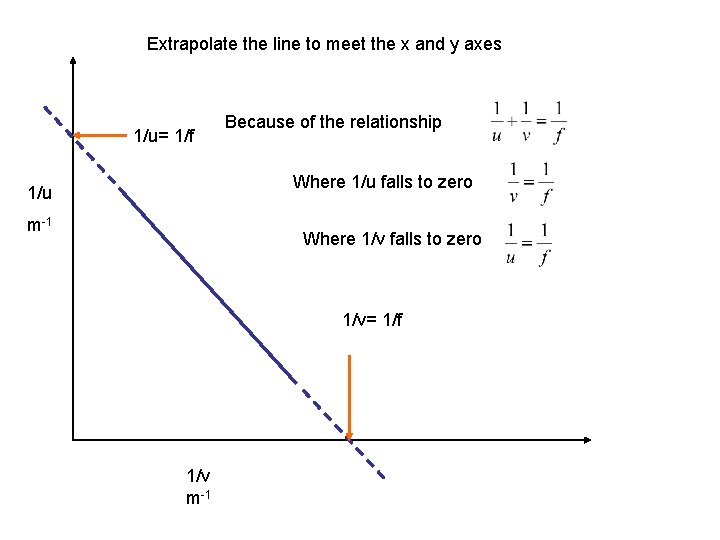
Extrapolate the line to meet the x and y axes 1/u= 1/f Because of the relationship Where 1/u falls to zero 1/u m-1 Where 1/v falls to zero 1/v= 1/f 1/v m-1