Lectures on Cellular Automata Continued Modified and upgraded

Lectures on Cellular Automata Continued Modified and upgraded slides of Martijn Schut schut@cs. vu. nl Vrij Universiteit Amsterdam Lubomir Ivanov Department of Computer Science Iona College and anonymous from Internet

Dynamical Systems and Cellular Automata Morphogenetic modeling

Organisms are dissipative processes in space and time matter energy matter heat entropy dissipator

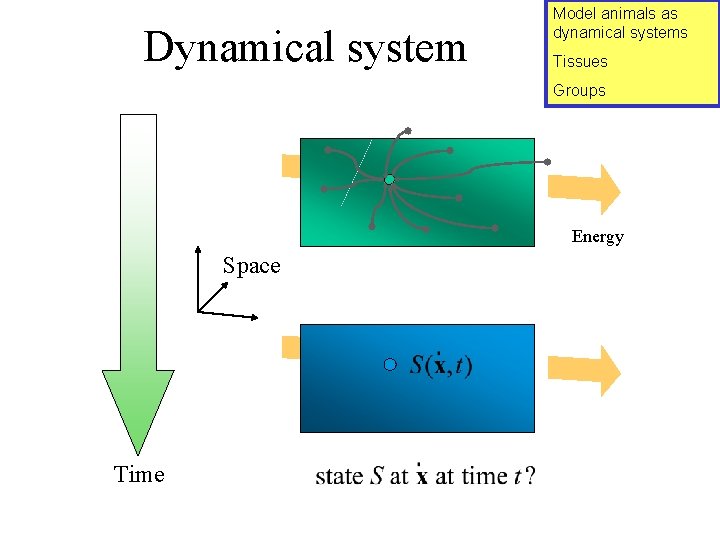
Dynamical system Model animals as dynamical systems Tissues Groups Energy Space Time

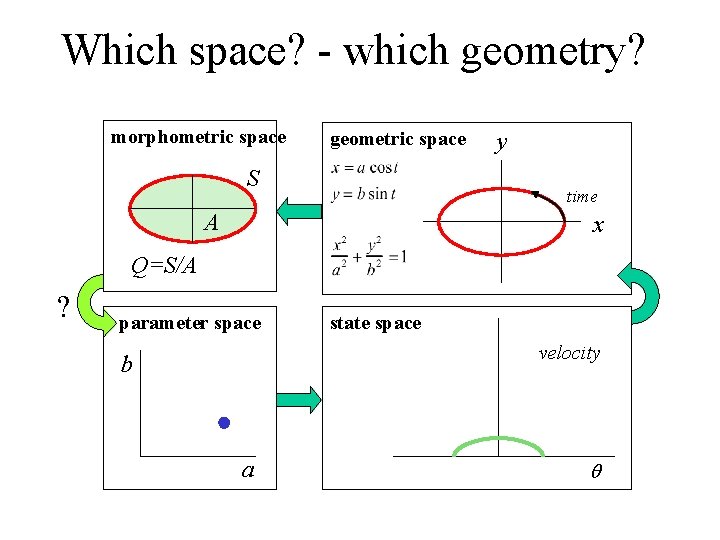
Which space? - which geometry? morphometric space geometric space S y time A x Q=S/A ? parameter space state space velocity b a q

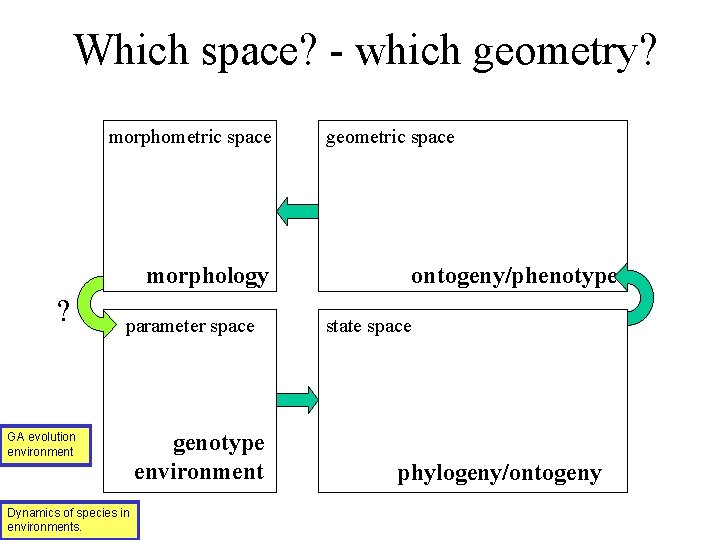
Which space? - which geometry? morphometric space morphology ? parameter space GA evolution environment Dynamics of species in environments. genotype environment geometric space ontogeny/phenotype state space phylogeny/ontogeny

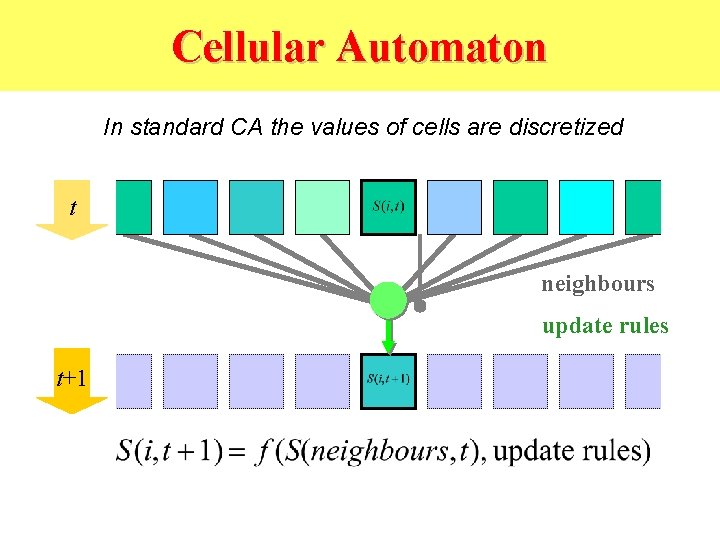
Discretization has many aspects t • discrete time steps T=0, 1, 2, 3, … • discrete cells at X, Y, Z=0, 1, 2, 3, . . . • discretize cell states S=0, 1, 2, 3, . . . We can mix discrete and continuous values in some models t+1 t+2

Cellular Automaton In standard CA the values of cells are discretized t neighbours update rules t+1

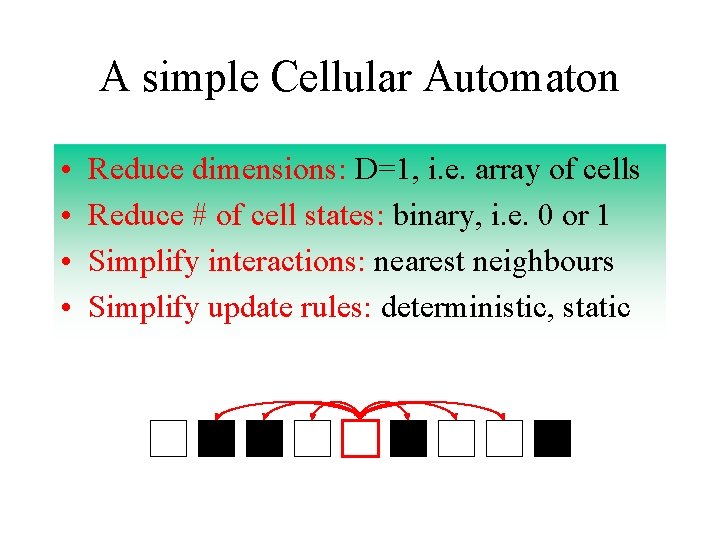
A simple Cellular Automaton • • Reduce dimensions: D=1, i. e. array of cells Reduce # of cell states: binary, i. e. 0 or 1 Simplify interactions: nearest neighbours Simplify update rules: deterministic, static

Effects of simplification CA mo d el S pa ti al d is c reti za ti on Mor ph oge n esi s ~ le ve l o f d e tai l (organi sm , ce ll, mo le c ul e) T em pora l d isc reti za ti on ~ le ve l o f d e tai l (cel l cy cl e , reac tio n rate) R e duc ti on o f d im en s ion pro found e ff ec ts (2 D “G am e of Li fe” ) B ina ri za ti on co m pu ta ti ona l conven ience nea re st -ne ighbou r in te rac ti ons sim p le upda te ru les; sim u lt ane it y , ub iqu it y ~ spa ti al re st ricti on s (01 A , 1 0 T, 00 G , 1 1 C ) ~ non- li nea rit y p rofound effe ct s

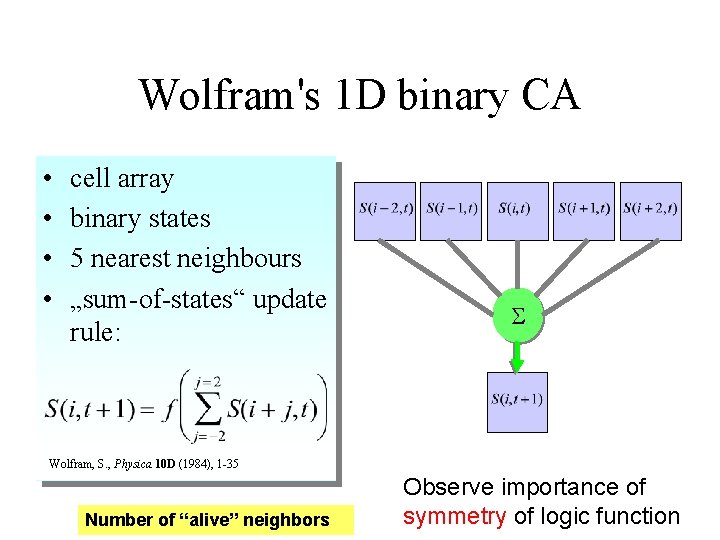
Wolfram's 1 D binary CA • • cell array binary states 5 nearest neighbours „sum-of-states“ update rule: S Wolfram, S. , Physica 10 D (1984), 1 -35 Number of “alive” neighbors Observe importance of symmetry of logic function

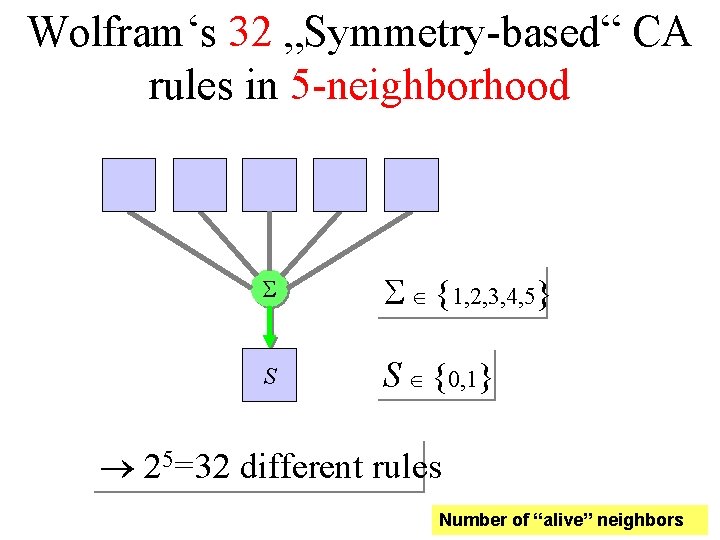
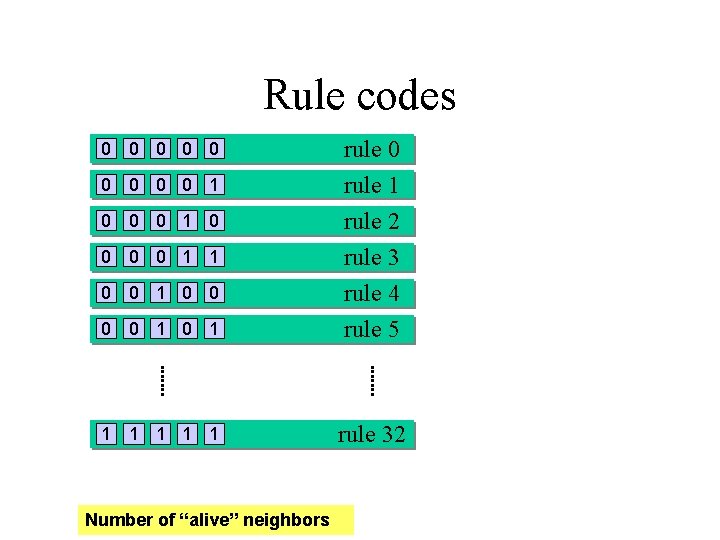
Wolfram‘s 32 „Symmetry-based“ CA rules in 5 -neighborhood S S {1, 2, 3, 4, 5} S S {0, 1} 25=32 different rules Number of “alive” neighbors

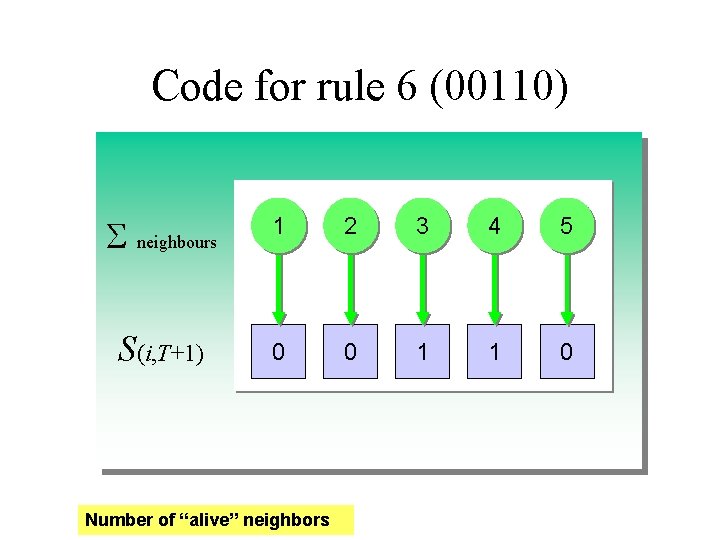
Code for rule 6 (00110) S neighbours 1 2 3 4 5 S(i, T+1) 0 0 1 1 0 Number of “alive” neighbors

Rule codes 0 0 1 rule 0 rule 1 rule 2 rule 3 rule 4 rule 5 1 1 1 rule 32 0 0 0 0 0 1 1 0 0 Number of “alive” neighbors

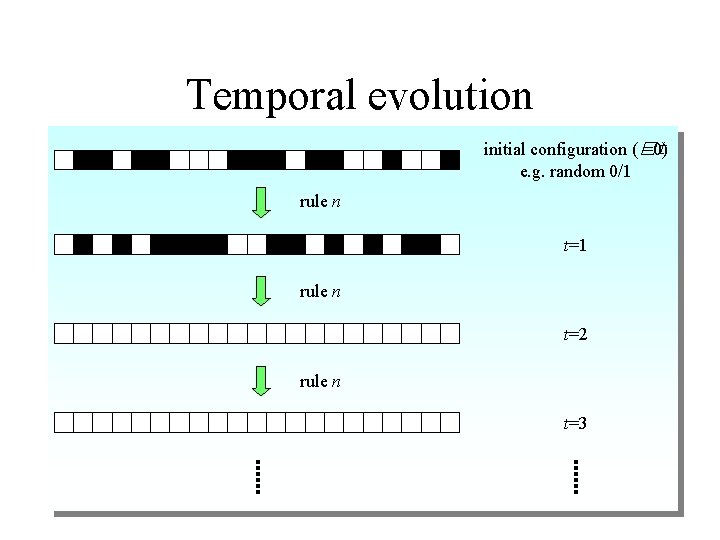
Temporal evolution initial configuration (�t =0) e. g. random 0/1 rule n t=2 rule n t=3

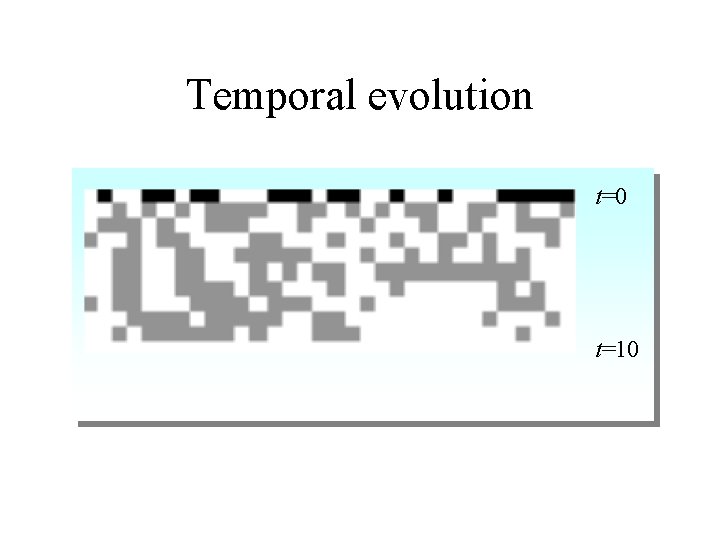
Temporal evolution t=0 t=10

Rule 6: 00110 t=100

Rule 10: 01010 t=100

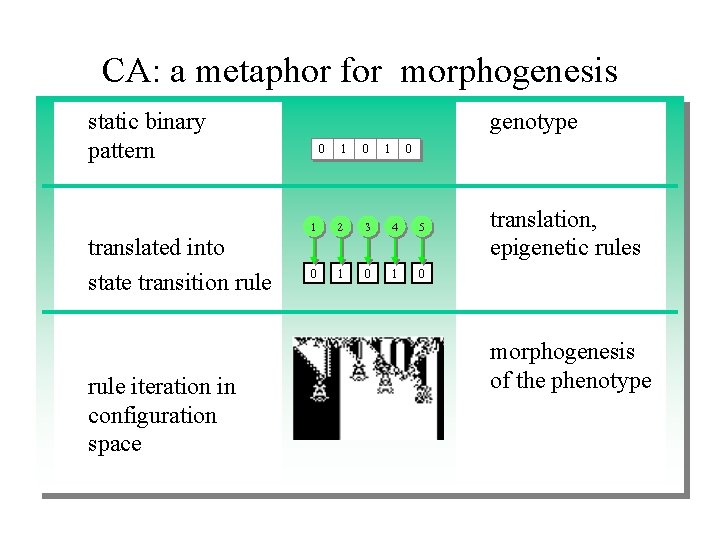
CA: a metaphor for morphogenesis static binary pattern translated into state transition rule iteration in configuration space genotype 0 1 0 1 2 3 4 5 0 1 0 translation, epigenetic rules morphogenesis of the phenotype

CA: a model for morphogenesis update rule genotype iterative application of the update rule epigenetic interpretation of the genotype, morphogenesis CA state pattern phenotype state space morphospace

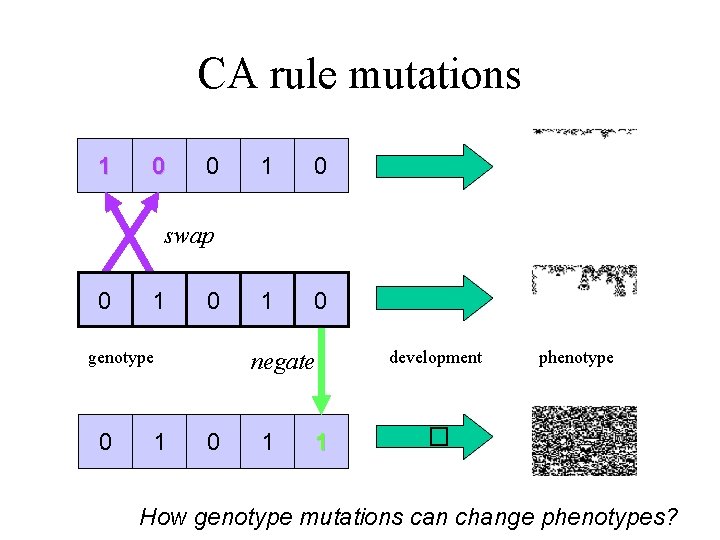
CA rule mutations 1 0 0 1 0 swap 0 1 0 genotype 0 1 negate 0 1 1 development phenotype � How genotype mutations can change phenotypes?

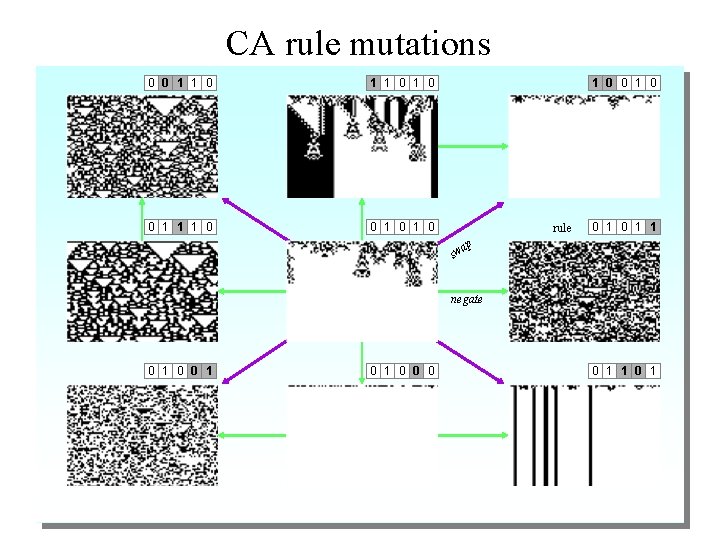
CA rule mutations 0 0 1 1 0 1 0 0 1 1 1 0 0 1 0 1 0 rule 0 1 1 ap sw negate 0 1 0 1 0 0 1 1 0 1

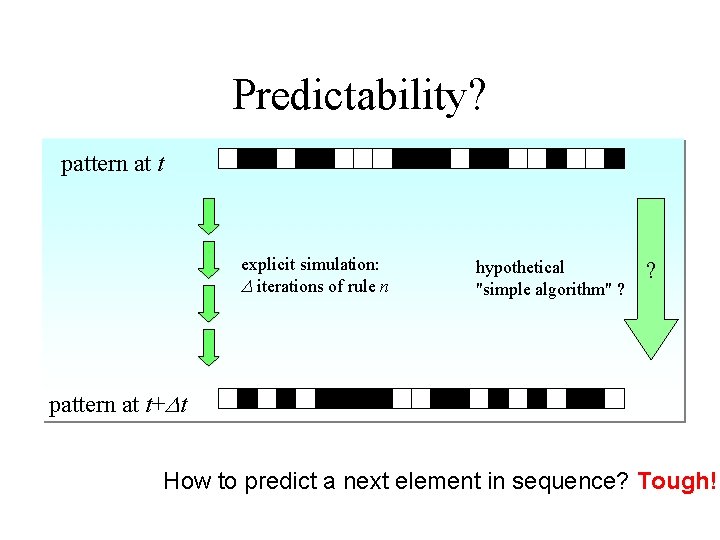
Predictability? pattern at t explicit simulation: D iterations of rule n hypothetical "simple algorithm" ? ? pattern at t+Dt How to predict a next element in sequence? Tough!

Predictability Sum of natural numbers 1… N Nth prime number algorithm 1: 1+2+…+N algorithm 1: trial and error algorithm 2: N(N+1)/2 (Gaussian formula) algorithm 2: ? no general formula easy Very tough!

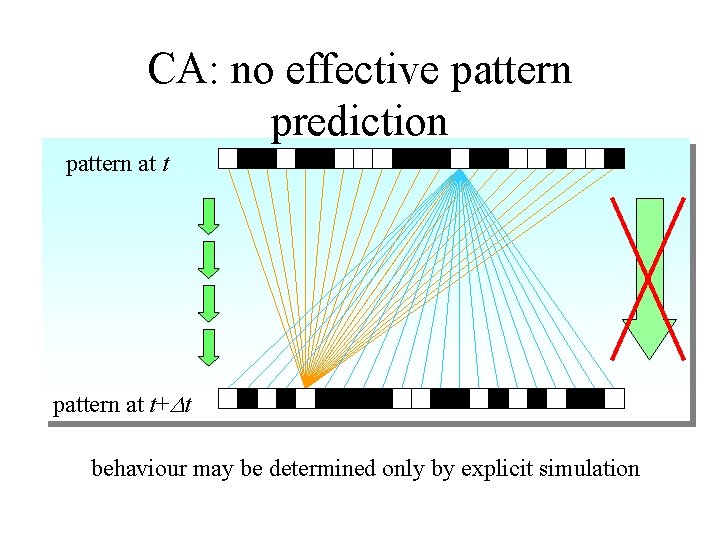
CA: no effective pattern prediction pattern at t+Dt behaviour may be determined only by explicit simulation

CA: deterministic, unpredictable, irreversible • Simple rules generate complex spatiotemporal behavior • For non-trivial rules, the spatio-temporal behaviour is computable but not predictable • The behavior of the system is irreversible • Similarity of rules does not imply similarity of patterns

Aspects of CA morphogenesis • complex relationship between „genotype“ and „phenotype • effects of „genes“ are not localizable in specific phenes (pleiotropy) • phenes cannot be traced back to specific single genes (epistasis) epistasis • phenetic effects of "mutations" are not predictable

Meinhardt, H. (1995). The Algorithmic Beauty of Sea Shells. Berlin: Springer

Patterns and morphology • Pattern: a spatially and/or temporally ordered distribution of a physical or chemical parameter • Pattern formation • Form (Size and Shape) • Morphogenesis: The spatiotemporal processes by which an organism changes is size (growth) and shape (development)

Where is the phene? phenotype A • Typification? • Comparative measures? – length – density – fractal dimension • Spatio-temporal development? phenotype B