Lectures 8 9 abg decay theory Nov 2006

Lectures 8 & 9 ab[g] decay theory Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 1

8. 0 Overview n n n 8. 1 QM tunnelling and a decays 8. 2 Fermi theory of b decay and electron capture 8. 3 The Cowan and Reines Experiment 8. 4 The Wu experiment 8. 5 g decays (very brief) Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 2

abg Decay Theory n n n Previously looked at kinematics and energetics now study the dynamics i. e. the interesting bit. Will need this to calculate life times Will get to understand variations in lifetimes Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 3

8. 1 a Decay Theory n n n Consider 232 Th, Z=90, with radius of R=7. 6 fm It alpha decays with Ea=4. 08 Me. V at r= But at R=7. 6 fm the potential energy of the alpha would be Ea, pot=34 Me. V if we believe: which we really should! n n Question: How does the a escape from the Th nucleus? Answer: by QM tunnelling Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 4

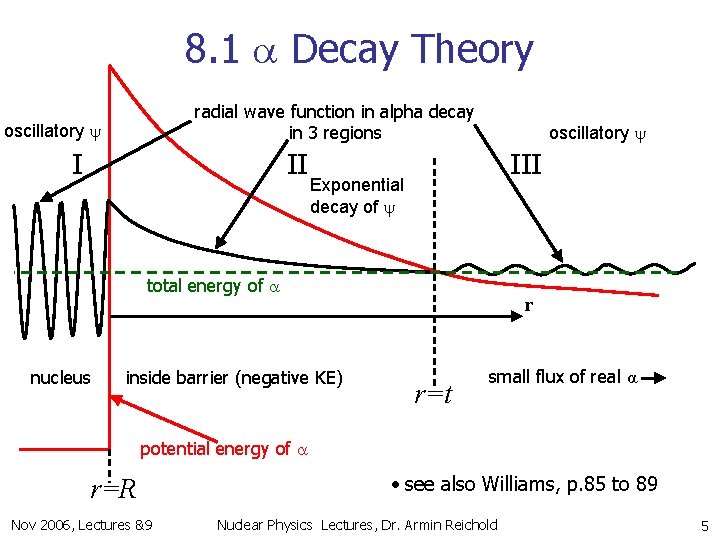
8. 1 a Decay Theory radial wave function in alpha decay in 3 regions oscillatory y I II oscillatory y III Exponential decay of y total energy of a nucleus inside barrier (negative KE) r r=t small flux of real α potential energy of a r=R Nov 2006, Lectures &9 • see also Williams, p. 85 to 89 Nuclear Physics Lectures, Dr. Armin Reichold 5

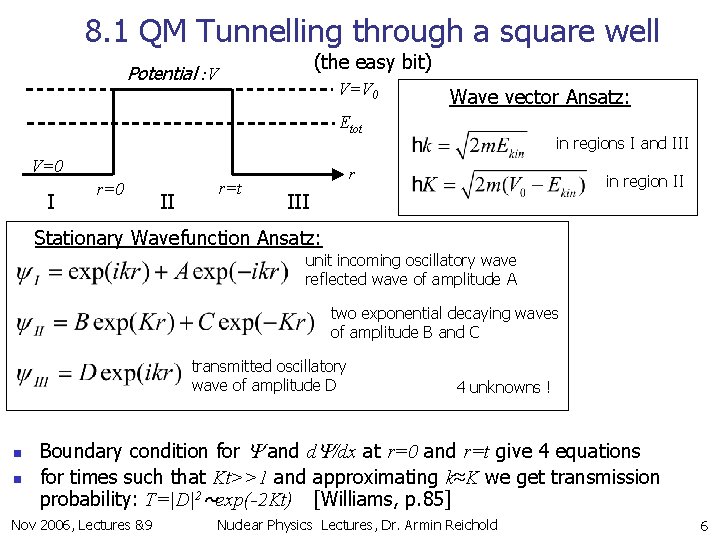
8. 1 QM Tunnelling through a square well (the easy bit) Potential : V V=V 0 Wave vector Ansatz: Etot V=0 I r=0 II r=t in regions I and III r in region II III Stationary Wavefunction Ansatz: unit incoming oscillatory wave reflected wave of amplitude A two exponential decaying waves of amplitude B and C transmitted oscillatory wave of amplitude D n n 4 unknowns ! Boundary condition for Y and d. Y/dx at r=0 and r=t give 4 equations for times such that Kt>>1 and approximating k≈K we get transmission probability: T=|D|2~exp(-2 Kt) [Williams, p. 85] Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 6

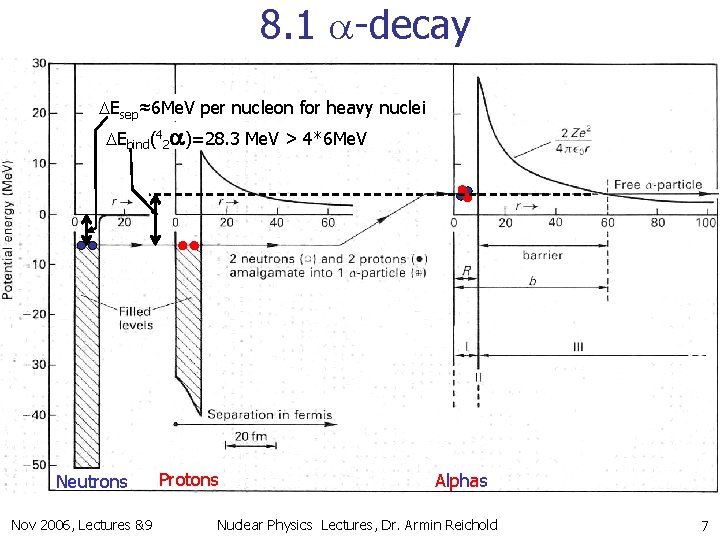
8. 1 a-decay DEsep≈6 Me. V per nucleon for heavy nuclei DEbind(42 a)=28. 3 Me. V > 4*6 Me. V Neutrons Nov 2006, Lectures &9 Protons Alphas Nuclear Physics Lectures, Dr. Armin Reichold 7

8. 1 Tunnelling in a-decay n n n Assume there is no recoil in the remnant nucleus Assume we can approximate the Coulomb potential by sequence of many square wells of thickness Dr with variable height Vi Transmission probability is then product of many T factors where the K inside T is a function of the potential: n The region between R and Rexit is defined via: V(r)>Ekin Inserting K into the above gives: n We call G the Gamov factor n Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 8

8. 1 Tunnelling in a-decay n Use the Coulomb potential for an a particle of charge Z 1 and a nucleus of charge Z 2 for V(r) the latter defines the relation between the exit radius and the alpha particles kinetic energy and Z 1=2 gives inserted into: Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 9

8. 1 Tunnelling in a-decay n How can we simplify this ? n n for nuclei that actually do a-decay we know typical decay energies and sizes Rtyp≈10 fm, Etyp ≈ 5 Me. V, Ztyp ≈ 80 Rexit, typ ≈ 60 fm >>Rtyp since n Inserting all this into G gives: n And further expressing Rexit via Ekin gives: Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 10

n n n 8. 1 a-decay Rates How can we turn the tunnelling probability into a decay rate? We need to estimate the “number of hits” that an a makes onto the inside surface of a nucleus. Assume: n n n the a already exists in the nucleus it has a velocity v 0=(2 Ekin/m)1/2 it will cross the nucleus in Dt=2 R/v 0 it will hit the surface with a rate of w 0=v 0/2 R Decay rate w is then “rate of hits” x tunnelling probability Note: w 0 is a very rough plausibility estimate! Williams tells you how to do it better but he can’t do it either! Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 11

8. 1 a-decay experimental tests n n n Predict exponential decay rate proportional to (Ekin)1/2 Agrees approximately with data for even-even nuclei. But angular momentum effects complicate the picture: n n n Additional angular momentum barrier (as in atomic physics) El is small compared to ECoulomb E. g. l=1, R=15 fm El~0. 05 Me. V compared to Z=90 Ecoulomb~17 Me. V. but still generates noticeable extra exponential suppression. Spin (DJ) and parity (DP) change from parent to daughter DJ=La Nov 2006, Lectures &9 DP=(-1)L Nuclear Physics Lectures, Dr. Armin Reichold 12

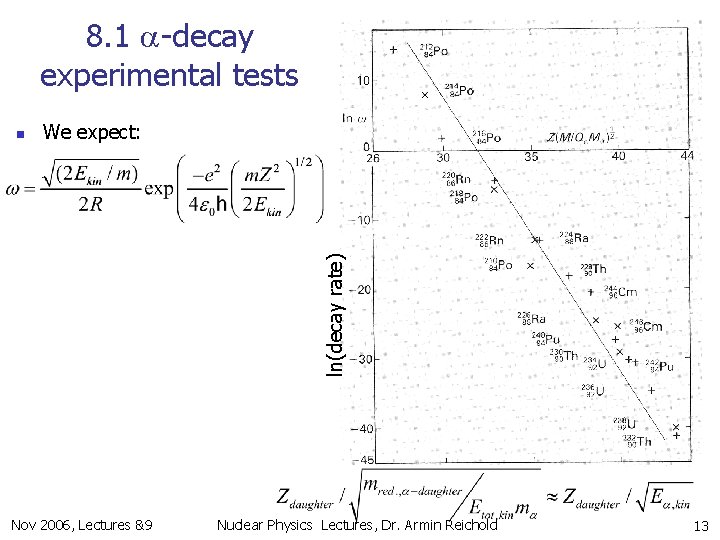
8. 1 a-decay experimental tests We expect: ln(decay rate) n Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 13

8. 2 Fermi b Decay Theory n n Consider simplest case: of bdecay, i. e. n decay At quark level: d u+W followed by decay of virtual W to electron + antineutrino this section is close to Cottingham & Greenwood p. 166 - ff but also check that you understand Williams p. 292 ff Nov 2006, Lectures &9 p d u u n d u e- d Nuclear Physics Lectures, Dr. Armin Reichold W- ne ( ) 14

8. 2 Fermi Theory n 4 point interaction n n d u d Energy of virtual W << m. W life time is negligible assume interaction is described by only a single number we call this number the Fermi constant of beta decay Gb also assume that p is heavy and does not recoil (it is often bound into an even heavier nucleus for other b-decays) We ignore parity non-conservation Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold d u u n p e- ne ( ) 15

8. 2 Fermi Theory n n n as we neglect nuclear recoil energy electron energy distribution is determined by density of states but pe and pn or Ee and En are correlated to conserve energy we can not leave them both variable Nov 2006, Lectures &9 16

8. 2 Fermi Theory Kurie Plot n FGR to get a decay rate and insert previous results: A let’s plot that from real data Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 17

8. 2 Electron Spectrum n n n Observe electron kinetic energy spectrum in tritium decay Implant tritium directly into a biased silicon detector Observe internal ionisation (electron hole pairs) generated from the emerging electron as current pulse in the detector number of pairs proportional to electron energy Observe continuous spectrum neutrino has to carrie the rest of the energy End point of this spectrum is function of neutrino mass But this form of spectrum is bad for determining the endpoint accurately Nov 2006, Lectures &9 Simple Spectrum Relative Intensity n Nuclear Physics Lectures, Dr. Armin Reichold Ekin, e (ke. V) 18

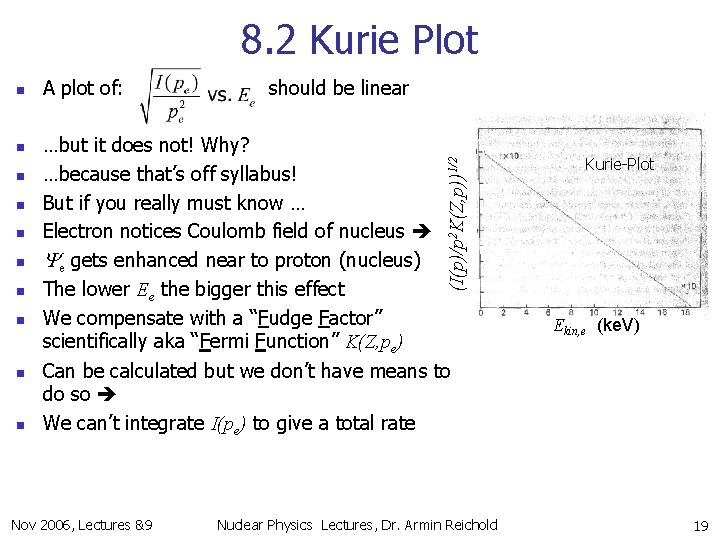
8. 2 Kurie Plot n n n n n A plot of: should be linear …but it does not! Why? …because that’s off syllabus! But if you really must know … Electron notices Coulomb field of nucleus Ye gets enhanced near to proton (nucleus) The lower Ee the bigger this effect We compensate with a “Fudge Factor” scientifically aka “Fermi Function” K(Z, pe) Can be calculated but we don’t have means to do so We can’t integrate I(pe) to give a total rate Nov 2006, Lectures &9 (I(p)/p 2 K(Z, p))1/2 n Nuclear Physics Lectures, Dr. Armin Reichold Kurie-Plot Ekin, e (ke. V) 19

8. 2 Selection Rules n Fermi Transitions: n n n Gamow-Teller transitions: n n n en couple to give spin Sen=0 “Allowed transitions” Len=0 DJn p=0. en couple to give spin Sen=1 “Allowed transitions” Len=0 DJn p=0 or ± 1 “Forbidden” transitions n n n See arguments on slide 15 Higher order terms correspond to non-zero DL. Therefore suppressed depending on (q. r)2 L Usual QM rules give: DJn p=Len+Sen Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 20

8. 2 Electron Capture n capture atomic electron Can compete with b+ decay. Use FGR again and first look at matrix element n For “allowed” transitions we consider Ye and Yn const. n Only le=0 has non vanishing Ye(r=0) and for ne=1 this is largest. n n Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 21

8. 2 Electron Capture n Density of states easier now n n only a 2 -body final state (n, n) n is assumed approximately stationary only n matters final state energy = En apply Fermi’s Golden Rule AGAIN: Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 22

n n n 8. 3 Anti-neutrino Discovery Inverse Beta Decay Assume again no recoil on n But have to treat positron fully relativistic Same matrix elements as b-decay because all wave functions assume to be plane waves Fermi’s Golden Rule (only positron moves in final state!) Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 23

8. 3 Anti-neutrino Discovery n Phase space factor: n Neglect neutron recoil: n Combine with FGR Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 24

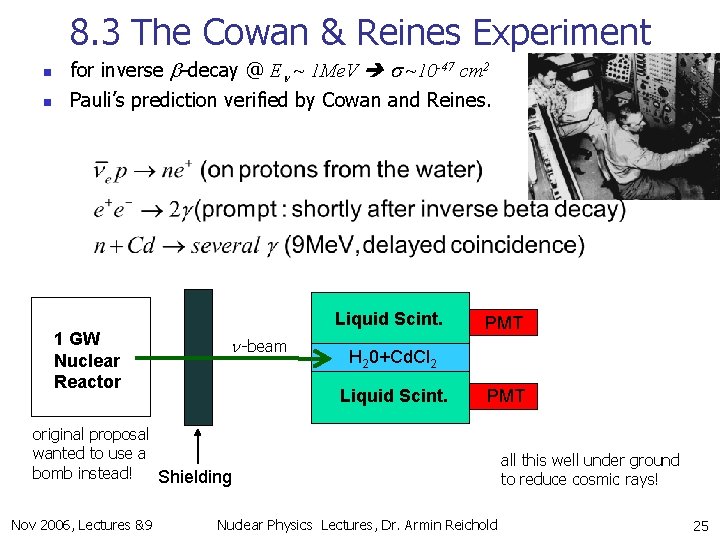
8. 3 The Cowan & Reines Experiment n n for inverse b-decay @ En ~ 1 Me. V s ~10 -47 cm 2 Pauli’s prediction verified by Cowan and Reines. 1 GW Nuclear Reactor Liquid Scint. n -beam PMT H 20+Cd. Cl 2 Liquid Scint. PMT original proposal wanted to use a bomb instead! Shielding Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold all this well under ground to reduce cosmic rays! 25

8. 4 Parity Definitions n n n Parity transforms from a left to a right handed co-ordinate system and vice versa Eigenvalues of parity are +/- 1. If parity is conserved: [H, P]=0 eigenstates of H are eigenstates of parity all observables have a defined parity If Parity is conserved all result of an experiment should be unchanged by parity operation If parity is violated we can measure observables with mixed parity, i. e. not eigenstates of parity best read Bowler, Nuclear Physics, chapter 2. 3 on parity! 26

Parity Conservation n n n If parity is conserved for reaction a + b c + d. Absolute parity of states that can be singly produced from vacuum (e. g. photons hg= -1) can be defined wrt. vacuum For other particles we can define relative parity. e. g. arbitrarily define hp=+1, hn=+1 then we can determine parity of other nuclei wrt. this definition parity of anti-particle is opposite particle’s parity Parity is a hermitian operator as it has real eigenvalues! If parity is conserved <pseudo-scalar>=0 (see next transparency). Nuclei are Eigenstates of parity Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 27

Parity Conservation n Let Op be an observable pseudo scalar operator, i. e. [H, Op]=0 Let parity be conserved [H, P]=0 [P, Op]=0 Let Y be Eigenfunctions of P and H with intrinsic parity hp insert Unity as POp=-Op. P since [P, Op]=0 use E. V. of Y under parity n n <Op> = - <Op> = 0 QED it is often useful to think of parity violation as a non vanishing expectation value of a pseudo scalar operator Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 28

Q: Is Parity Conserved In Nature? n n A 1: Yes for all electromagnetic and strong interactions. Feynman lost his 100$ bet that parity was conserved everywhere. In 1956 that was a lot of money! A 2: Big surprise was that parity is violated in weak interactions. How was this found out? n n n can’t find this by just looking at nuclei. They are parity eigenstates (defined via their nuclear and EM interactions) must look at properties of leptons in beta decay which are born in the weak interaction see Bowler, Nuclear Physics, chapter 3. 13 Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 29

Mme. Wu’s “Cool” Experiment n n n Adiabatic demagnetisation to get T ~ 10 m. K Align spins of 60 Co with magnetic field. Measure angular distribution of electrons and photons relative to B field. Clear forward-backward asymmetry of the electron direction (forward=direction of B) Parity violation. 5+ Excitation Note: ~100% n n Spin S= axial vector Magnetic field B = axial vector Momentum p = real vector Parity will only flip p not B and S b - allowed Gamov Teller decay DJ=1 Nuclear Physics Lectures, Dr. Armin Reichold 2+ 0+ 60 Co Nov 2006, Lectures &9 4+ Energy 2. 51 Me. V 1. 33 Me. V 0 Me. V 60 Ni 30

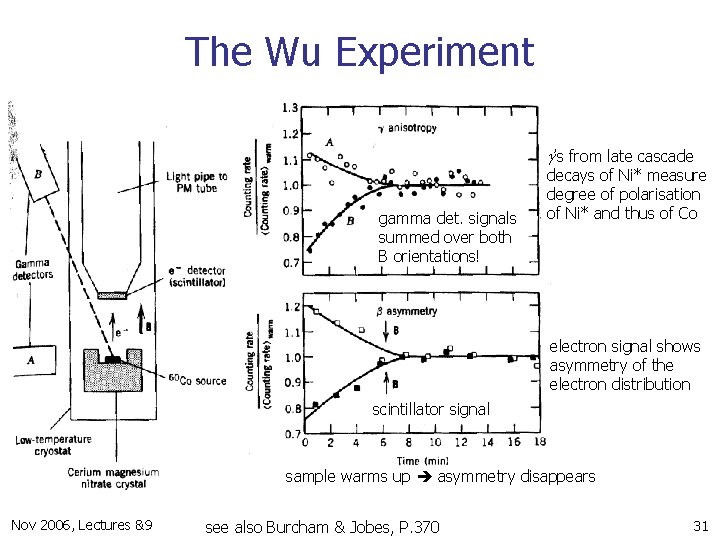
The Wu Experiment g’s from late cascade gamma det. signals summed over both B orientations! decays of Ni* measure degree of polarisation of Ni* and thus of Co electron signal shows asymmetry of the electron distribution scintillator signal sample warms up asymmetry disappears Nov 2006, Lectures &9 see also Burcham & Jobes, P. 370 31

Interpreting the Wu Experiment n Let’s make an observable pseudo scalar Op: n n Op=JCo * pe = Polarisation (axial vector dot real vector) If parity were conserved this would have a vanishing expectation value But we see that pe prefers to be anti-parallel to B and thus to JCo Thus: parity is violated Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 32

Improved Wu-Experiment n n n Nov 2006, Lectures &9 Polar diagram of angular dependence of electron intensity q is angle of electron momentum wrt spin of 60 Co or B using many detectors at many angles points indicate measurements if P conserved this would have been a circle centred on the origin Nuclear Physics Lectures, Dr. Armin Reichold 33

8. 5 g decays n When do they occur? n n n Nuclei have excited states similar to atoms. Don’t worry about details E, JP (need a proper shell model to understand). EM interaction less strong then the strong (nuclear) interaction Low energy excited states E<6 Me. V above ground state can’t usually decay by nuclear interaction g-decays important in cascade decays following a and b decays. Practical consequences n n n Fission. Significant energy released in g decays (see later lectures) Radiotherapy: g from Co 60 decays Medical imaging eg Tc (see next slide) Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 34

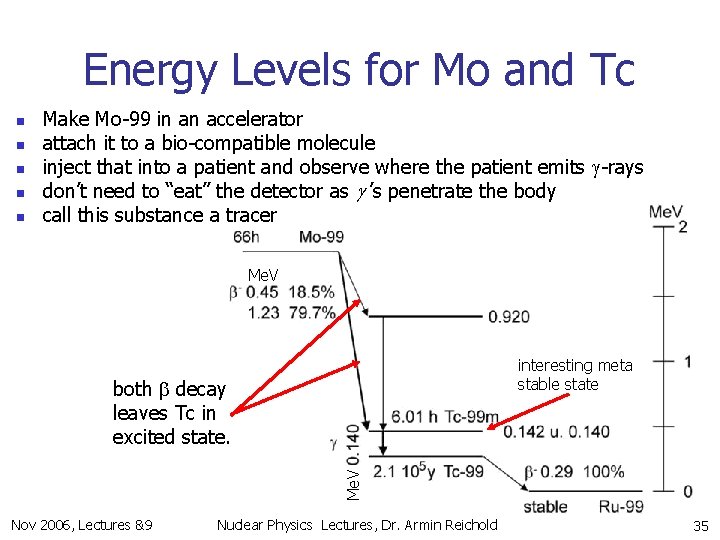
Energy Levels for Mo and Tc n n n Make Mo-99 in an accelerator attach it to a bio-compatible molecule inject that into a patient and observe where the patient emits g-rays don’t need to “eat” the detector as g ’s penetrate the body call this substance a tracer Me. V interesting meta stable state Me. V both b decay leaves Tc in excited state. Nov 2006, Lectures &9 Nuclear Physics Lectures, Dr. Armin Reichold 35