Lecture VI Electric Dipole Moments Beyond the Standard

Lecture VI: Electric Dipole Moments Beyond the Standard Model M. J. Ramsey-Musolf U Mass Amherst http: //www. physics. umass. edu/acfi/ ACFI EDM School November 2016 1

Lecture IV Outline I. General Considerations II. BSM Motivation III. Supersymmetry (Minimal Model) IV. Higgs Portal CPV: 2 Higgs Doublet Model V. Extended Gauge Sector: Left-Right Symmetric Model 2

I. General Considerations 3

Recall: SM EDMs 4

EDMs & SM Physics dn ~ (10 -16 e cm) x QCD + dn. CKM 5

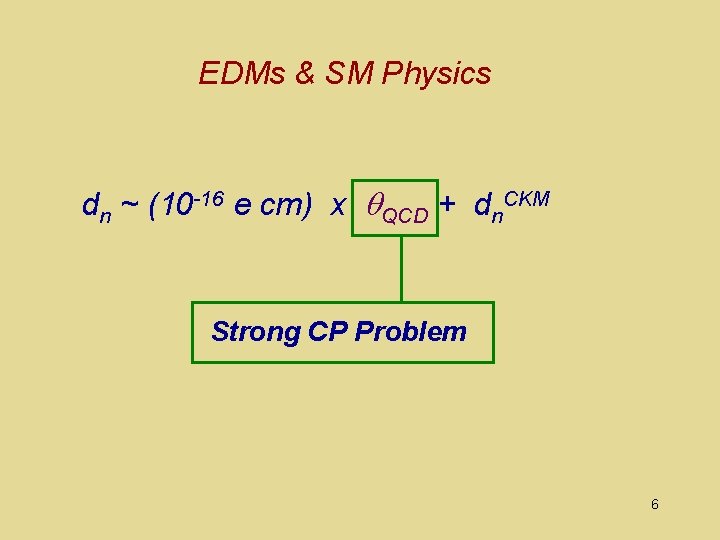
EDMs & SM Physics dn ~ (10 -16 e cm) x QCD + dn. CKM Strong CP Problem 6

EDMs & SM Physics dn ~ (10 -16 e cm) x QCD + dn. CKM Suppression factors • ( S = 1 CPV ) x ( S = 1 CPC ) • s 1 s 2 s 3 s • Multi loop 7

EDMs & SM Physics dn ~ (10 -16 e cm) x QCD + dn. CKM = (1 – 6) x 10 -32 e cm C. Seng ar. Xiv: 1411. 1476 8

EDMs & BSM Physics d ~ (10 -16 e cm) x (u / )2 x sin x yf F 9

EDMs & BSM Physics d ~ (10 -16 e cm) x (u / )2 x sin x yf F CPV Phase: large enough for baryogenesis ? 10

EDMs & BSM Physics d ~ (10 -16 e cm) x (u / )2 x sin x yf F BSM mass scale: Te. V ? Much higher ? u = 246 Ge. V > 246 Ge. V Higgs vacuum expectation value Mass scale of BSM physics 11

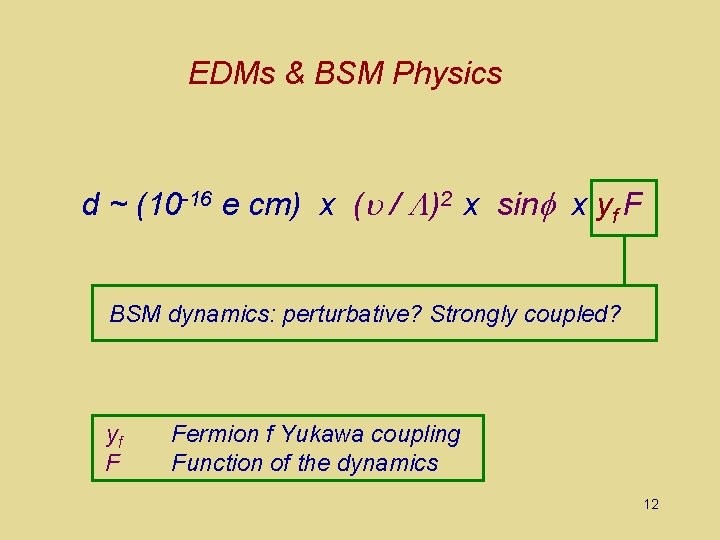
EDMs & BSM Physics d ~ (10 -16 e cm) x (u / )2 x sin x yf F BSM dynamics: perturbative? Strongly coupled? yf F Fermion f Yukawa coupling Function of the dynamics 12

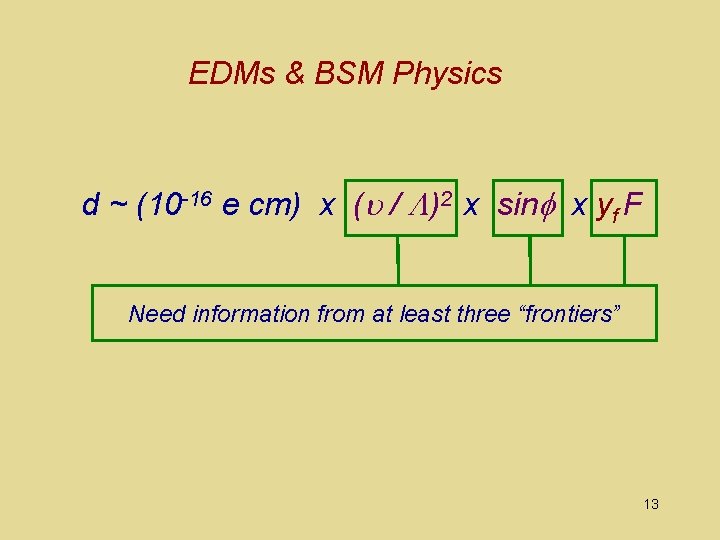
EDMs & BSM Physics d ~ (10 -16 e cm) x (u / )2 x sin x yf F Need information from at least three “frontiers” 13

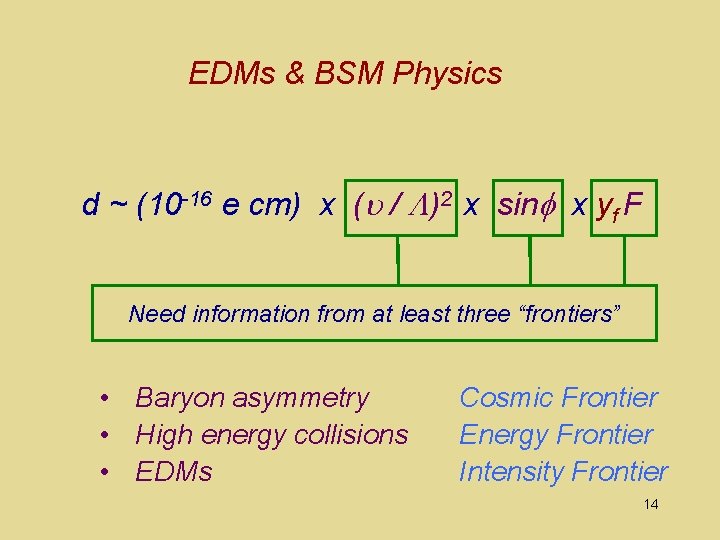
EDMs & BSM Physics d ~ (10 -16 e cm) x (u / )2 x sin x yf F Need information from at least three “frontiers” • Baryon asymmetry • High energy collisions • EDMs Cosmic Frontier Energy Frontier Intensity Frontier 14

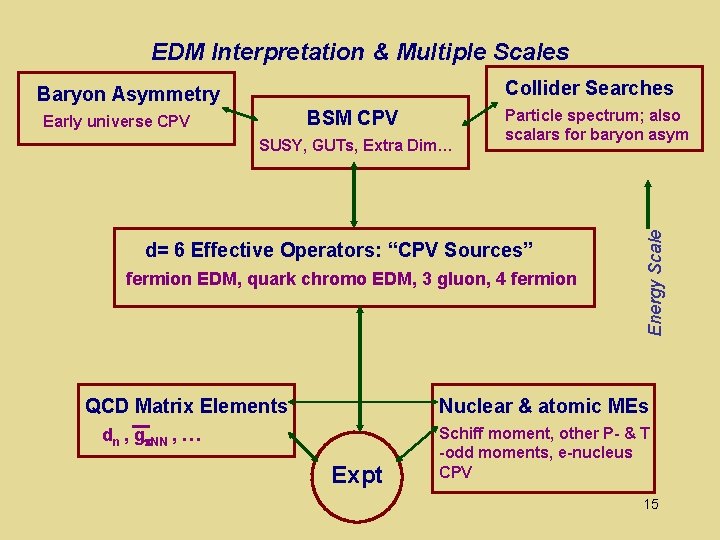
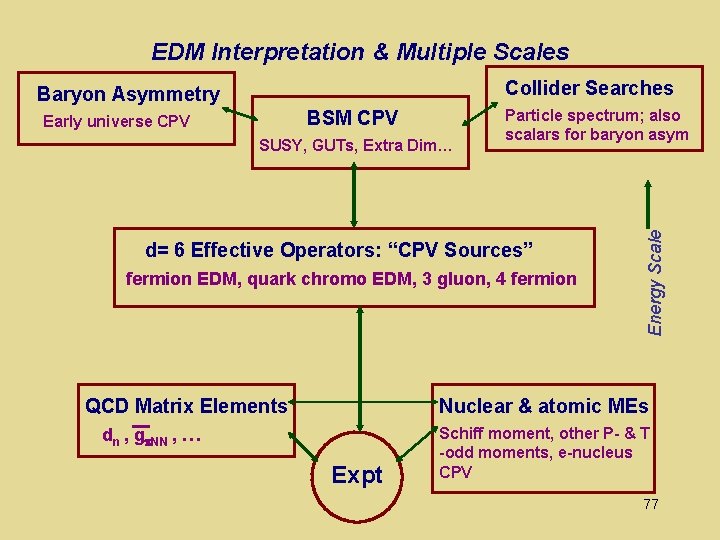
EDM Interpretation & Multiple Scales Collider Searches BSM CPV Early universe CPV SUSY, GUTs, Extra Dim… Particle spectrum; also scalars for baryon asym d= 6 Effective Operators: “CPV Sources” fermion EDM, quark chromo EDM, 3 gluon, 4 fermion QCD Matrix Elements Energy Scale Baryon Asymmetry Nuclear & atomic MEs dn , g NN , … Expt Schiff moment, other P- & T -odd moments, e-nucleus CPV 15

Wilson Coefficients: Summary f fermion EDM (3) q quark CEDM (2) CG~ 3 gluon (1) Cquqd non-leptonic (2) Clequ, ledq semi-leptonic (3) C ud induced 4 f (1) ~ 12 total + light flavors only (e, u, d) 16 16

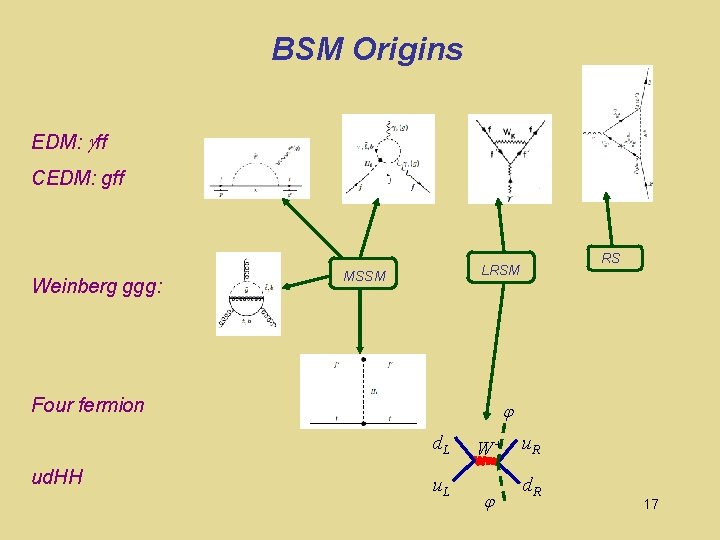
BSM Origins EDM: ff CEDM: gff Weinberg ggg: MSSM Four fermion ud. HH RS LRSM d. L W+ u. R u. L d. R 17

II. BSM Motivation 18

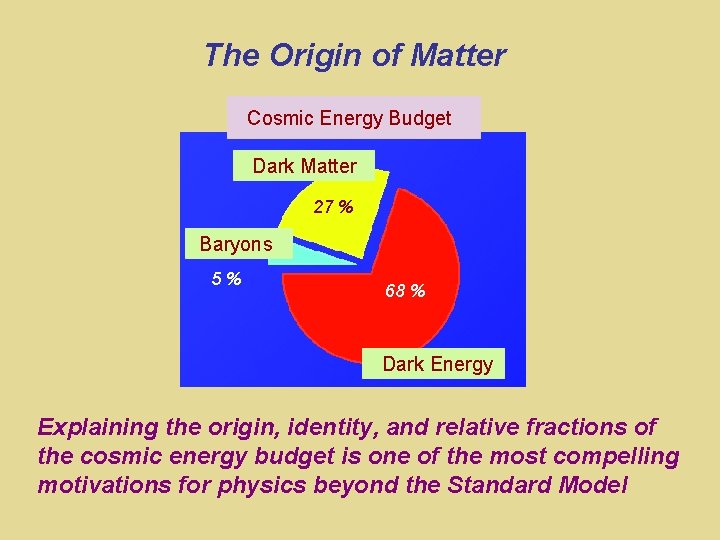
The Origin of Matter Cosmic Energy Budget Dark Matter 27 % Baryons 5% 68 % Dark Energy Explaining the origin, identity, and relative fractions of the cosmic energy budget is one of the most compelling motivations for physics beyond the Standard Model

Naturalness Problem 20

Scalar Fields in Particle Physics

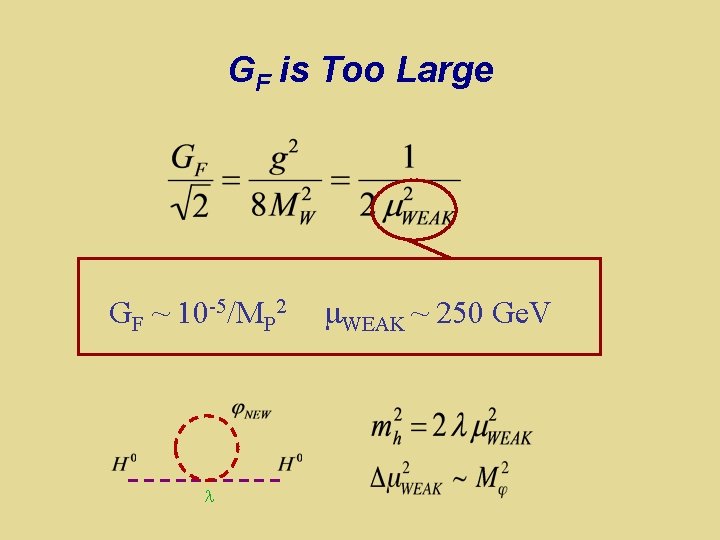
Scalar Fields in Particle Physics Scalar fields are a simple Scalar fields are theoretically problematic m 2 ~ 2 Discovery of a (probably) fundamental 125 Ge. V scalar : Is it telling us anything about ? Naturalness?

Scalar Fields in Particle Physics Scalar fields are a simple Scalar fields are theoretically problematic m 2 ~ 2 Discovery of a (probably) fundamental 125 Ge. V scalar : mh 2 ~ v 2 & GF ~ 1/v 2 : what keeps GF “large” ?

LHC Implications • Weak scale BSM physics (e. g. , SUSY) is there but challenging for the hadronic collider • BSM physics is there but a bit heavy (some fine tuning) • We are thinking about the problem incorrectly (cosmological constant? ? ? )

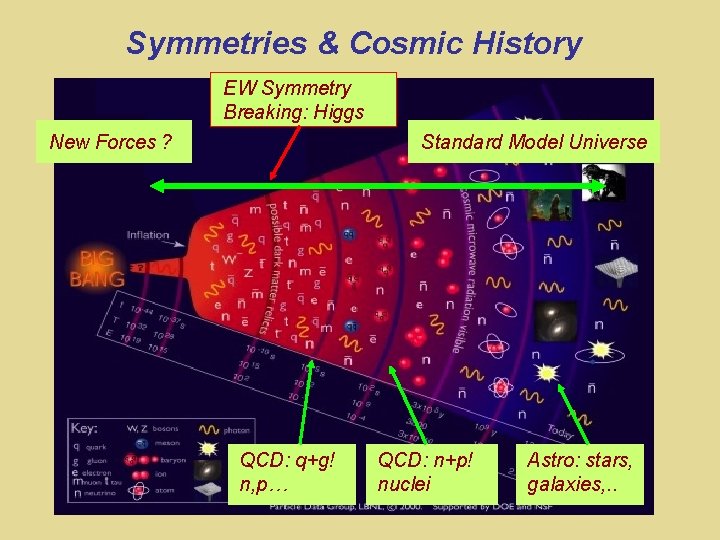
Symmetries & Cosmic History EW Symmetry Breaking: Higgs New Forces ? Standard Model Universe QCD: q+g! n, p… QCD: n+p! nuclei Astro: stars, galaxies, . .

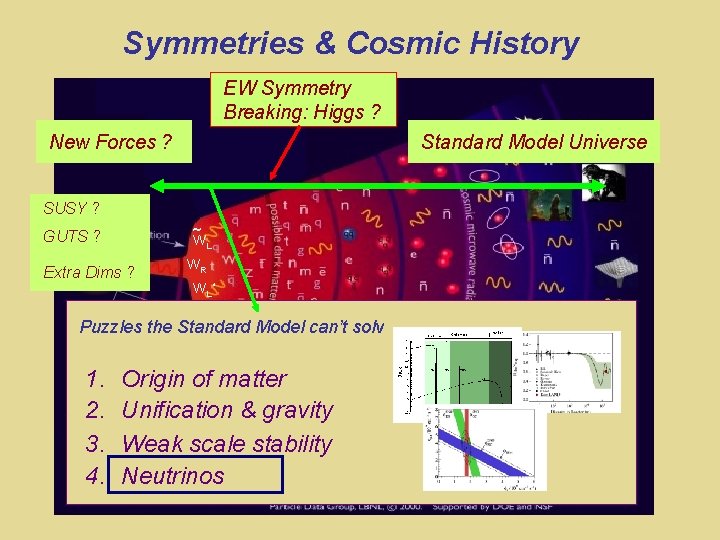
Symmetries & Cosmic History EW Symmetry Breaking: Higgs New Forces ? Standard Model Universe SUSY ? ~ GUTS ? WL Extra Dims ? WR WL* Puzzles the Standard Model can’t solve 1. 2. 3. 4. Origin of matter Unification & gravity Weak scale stability Neutrinos

Symmetries & Cosmic History EW Symmetry Breaking: Higgs New Forces ? SUSY ? GUTS ? Extra Dims ? Standard Model Universe ~ WL WR WL* Puzzles the Standard Model can’t solve 1. 2. 3. 4. Origin of matter Unification & gravity Weak scale stability Neutrinos

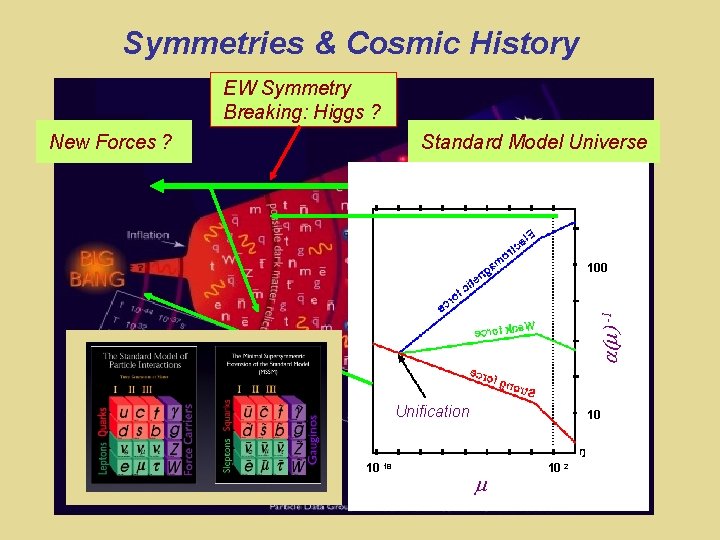
Symmetries & Cosmic History EW Symmetry Breaking: Higgs ? New Forces ? Standard Model Universe -1 100 “Near miss” for grand unification Unification g = g( ) 10 10 Desert 18 10 10 22 210

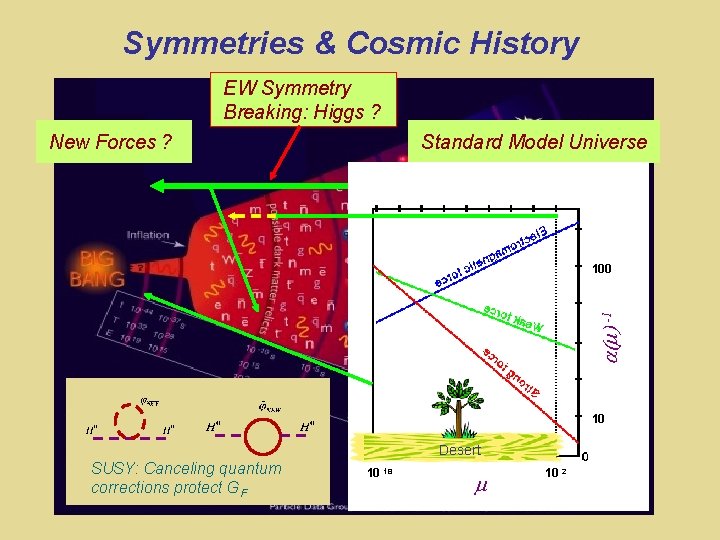
Symmetries & Cosmic History EW Symmetry Breaking: Higgs ? New Forces ? Standard Model Universe -1 100 10 Weak Int Rates: Solar burning g. Canceling = g( ) quantum SUSY: Element abundances corrections protect G F Desert 10 18 10 2

Symmetries & Cosmic History EW Symmetry Breaking: Higgs ? New Forces ? Standard Model Universe SUSY ? ~ GUTS ? WL Extra Dims ? WR WL* Puzzles the Standard Model can’t solve 1. 2. 3. 4. Origin of matter Unification & gravity Weak scale stability Neutrinos

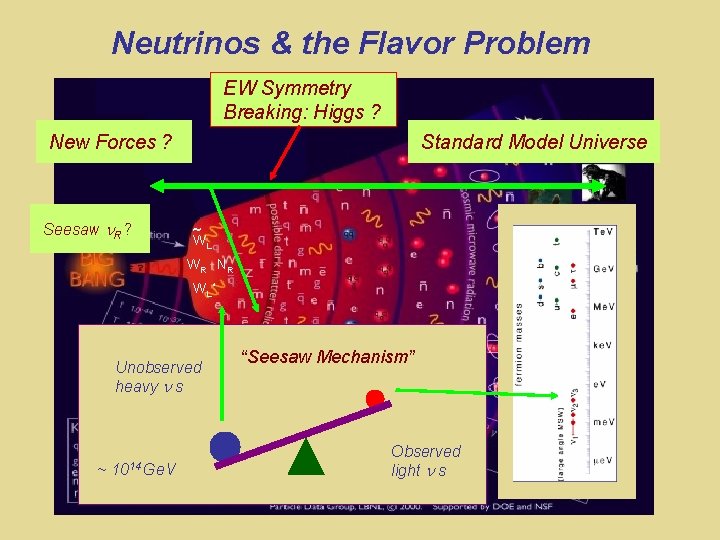
Neutrinos & the Flavor Problem EW Symmetry Breaking: Higgs ? New Forces ? Seesaw R ? Standard Model Universe ~ WL W R NR WL* New “Periodic “Seesaw Mechanism” Unobserved Table” heavy s Why so different ? ~ 1014 Ge. V Courtesy R. D. Mc. Keown Not physical states Observed light s

III. Supersymmetry 32

GF is Too Large GF ~ 10 -5/MP 2 l m. WEAK ~ 250 Ge. V

SUSY protects GF =0 if SUSY is exact

SUSY: a candidate symmetry of the early Universe • Unify all forces 3 of 4 • Protect GF from shrinking Yes • Produce all the matter that exists Maybe so • Account for neutrino properties Maybe • Give self-consistent quantum gravity Probably necessary

Minimal Supersymmetric Standard Two Higgs vevs Model (MSSM) No new coupling constants Supersymmetry Supersymmetric Higgs mass, Fermions Bosons sfermions gauginos Higgsinos Charginos, neutralinos

Minimal Supersymmetric Standard Model (MSSM)

SUSY and R Parity If nature conserves vertices have even number of superpartners Consequences § Lightest SUSY particle viable dark matter candidate § Proton is stable § Superpartners appear only in loops is stable

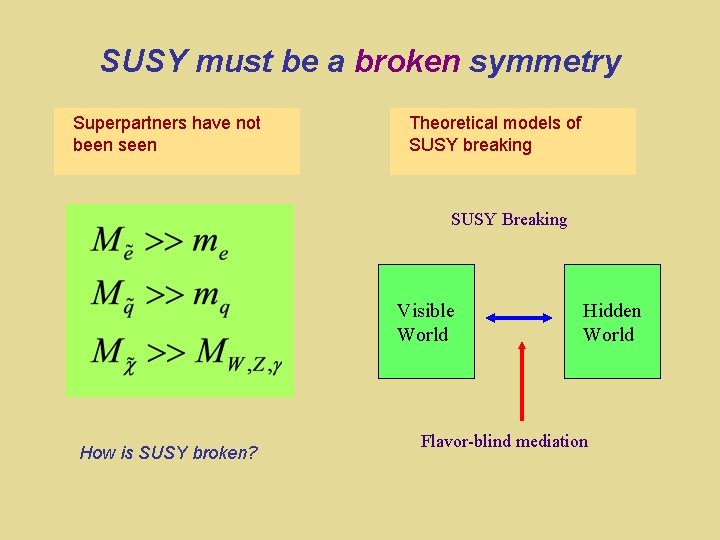
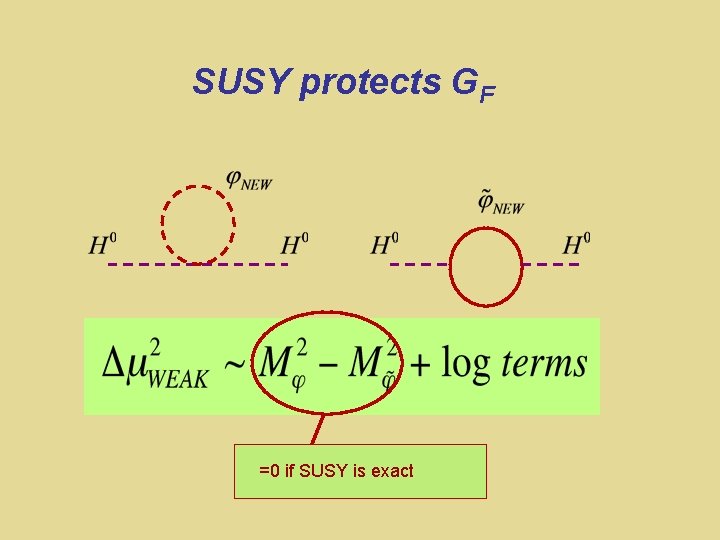
SUSY must be a broken symmetry Superpartners have not been seen Theoretical models of SUSY breaking SUSY Breaking Visible World How is SUSY broken? Hidden World Flavor-blind mediation

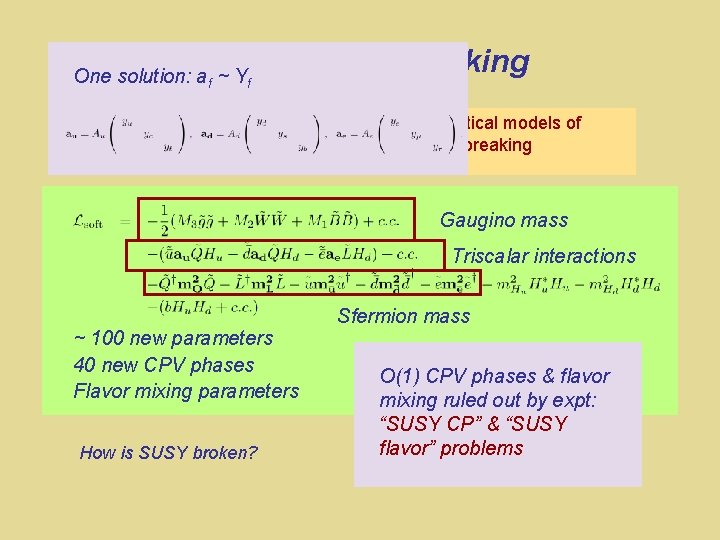
MSSM SUSY Breaking One solution: af ~ Yf Superpartners have not been seen Theoretical models of SUSY breaking Gaugino mass Triscalar interactions ~ 100 new parameters 40 new CPV phases Flavor mixing parameters How is SUSY broken? Sfermion mass O(1) CPV phases & flavor mixing ruled out by expt: “SUSY CP” & “SUSY flavor” problems

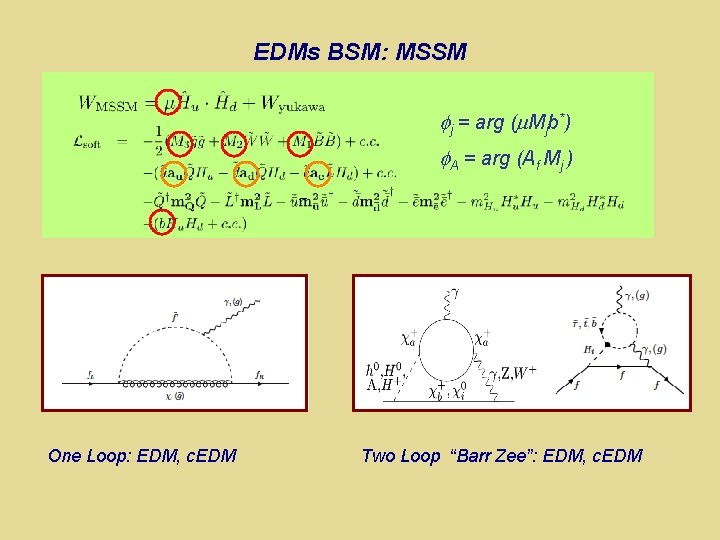
EDMs BSM: MSSM j = arg ( Mjb*) A = arg (Af Mj ) One Loop: EDM, c. EDM Two Loop “Barr Zee”: EDM, c. EDM

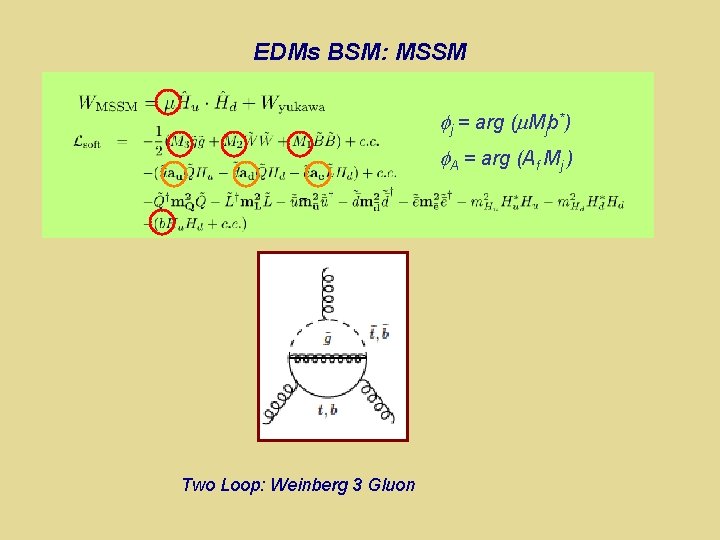
EDMs BSM: MSSM j = arg ( Mjb*) A = arg (Af Mj ) Two Loop: Weinberg 3 Gluon

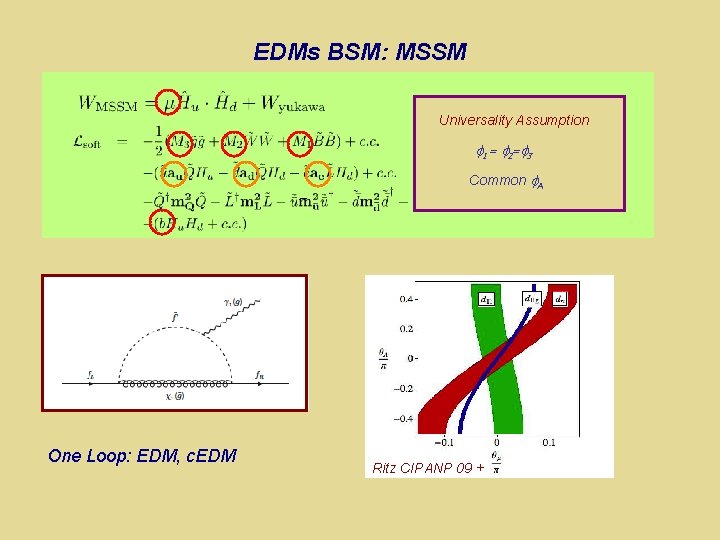
EDMs BSM: MSSM Universality = arg (Assumption M b*) j j A = arg (Af Mj ) Common A One Loop: EDM, c. EDM Ritz CIPANP 09 +

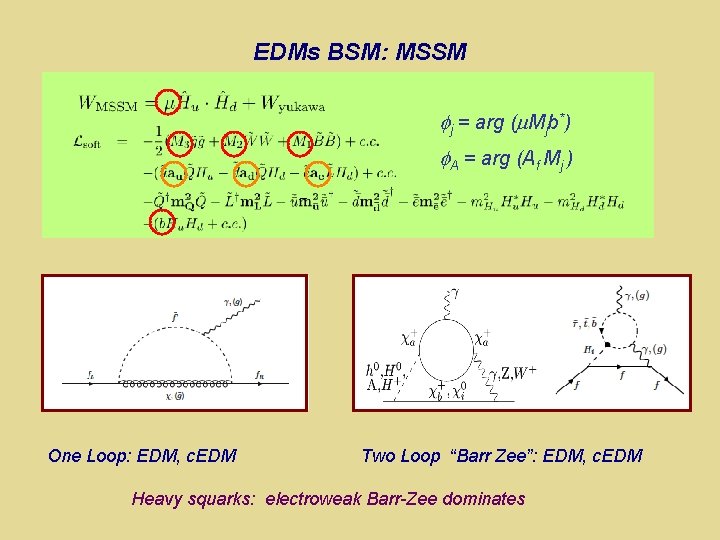
EDMs BSM: MSSM j = arg ( Mjb*) A = arg (Af Mj ) One Loop: EDM, c. EDM Two Loop “Barr Zee”: EDM, c. EDM Heavy squarks: electroweak Barr-Zee dominates

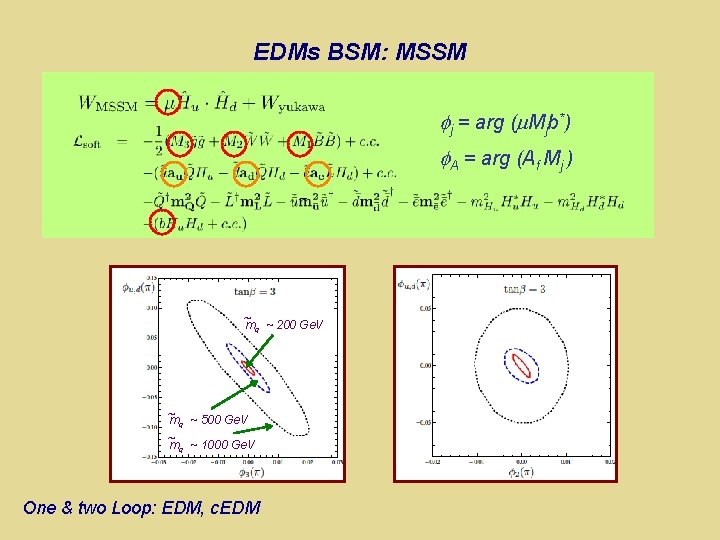
EDMs BSM: MSSM j = arg ( Mjb*) A = arg (Af Mj ) ~ mq ~ 200 Ge. V ~ mq ~ 500 Ge. V ~ m ~ 1000 Ge. V q One & two Loop: EDM, c. EDM

IV. Higgs Portal CPV 46

What is the CP Nature of the Higgs Boson ? • Interesting possibilities if part of an extended scalar sector 47

What is the CP Nature of the Higgs Boson ? • Interesting possibilities if part of an extended scalar sector • Two Higgs doublets ? H ! H 1 , H 2 48

What is the CP Nature of the Higgs Boson ? • Interesting possibilities if part of an extended scalar sector • Two Higgs doublets ? H ! H 1 , H 2 An example: MSSM but not most general due to restrictions of supersymmetry 49

What is the CP Nature of the Higgs Boson ? • Interesting possibilities if part of an extended scalar sector • Two Higgs doublets ? H ! H 1 , H 2 • New parameters: tan b = <H 1> / <H 2> sin b CPV ! 50

Two Higgs Double Model: Features Scalar Potential Complex parameters: m 122 & 5, 6, 7 51

Two Higgs Double Model: Features Yukawa Interactions • Notation: hj Matrices in flavor space (denoted Yj elsewhere) • “Type III 2 DHM” Both doublets couple to u. R & d. R 52

Two Higgs Double Model: Features Yukawa Interactions • Avoid “Flavor Changing Neutral Currents” : Place restrictions on the Yukawa couplings ! • “Type I & Type II 2 DHM” 53

Two Higgs Double Model: Features Yukawa Interactions • Avoid “Flavor Changing Neutral Currents” : Place restrictions on the Yukawa couplings ! • “Type I & Type II 2 DHM” 54

Two Higgs Double Model: Features Scalar Potential : CPV w/ “Z 2 Symmetry” Complex parameters: m 122 & 5 “Rephasing invariant”: 55

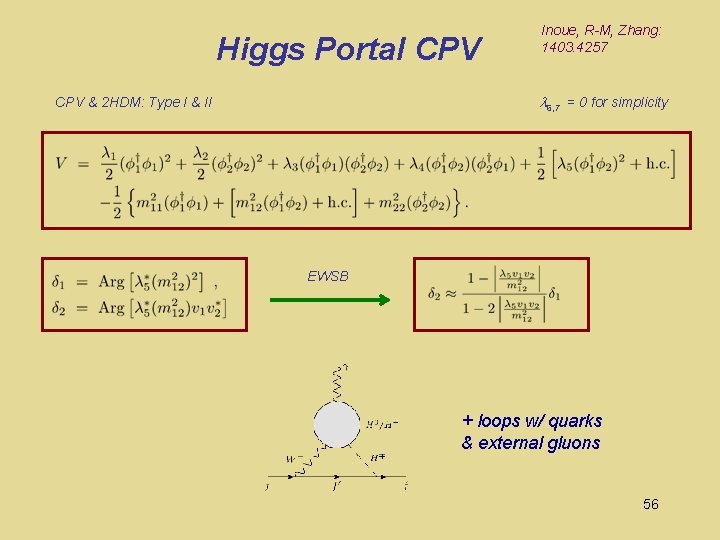
Higgs Portal CPV Inoue, R-M, Zhang: 1403. 4257 6, 7 = 0 for simplicity CPV & 2 HDM: Type I & II EWSB + loops w/ quarks & external gluons 56

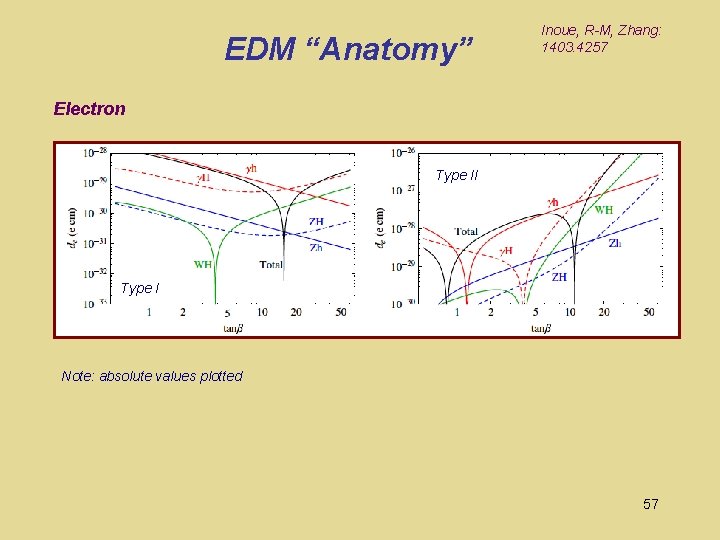
EDM “Anatomy” Inoue, R-M, Zhang: 1403. 4257 Electron Type II Type I Note: absolute values plotted 57

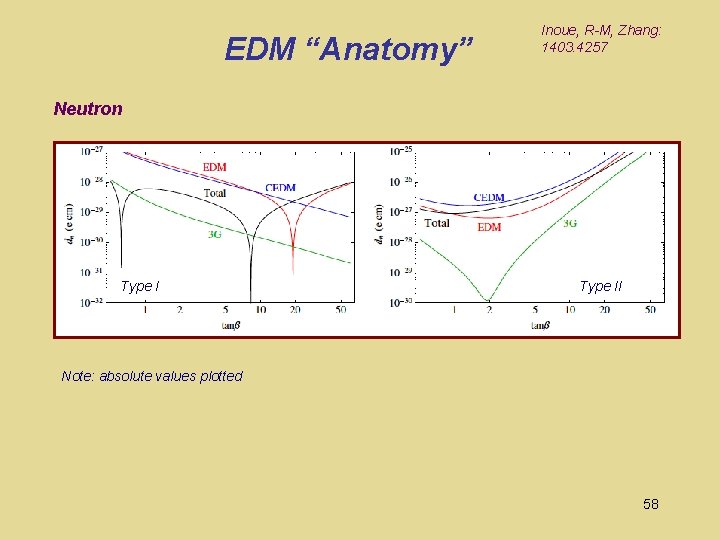
EDM “Anatomy” Inoue, R-M, Zhang: 1403. 4257 Neutron Type II Note: absolute values plotted 58

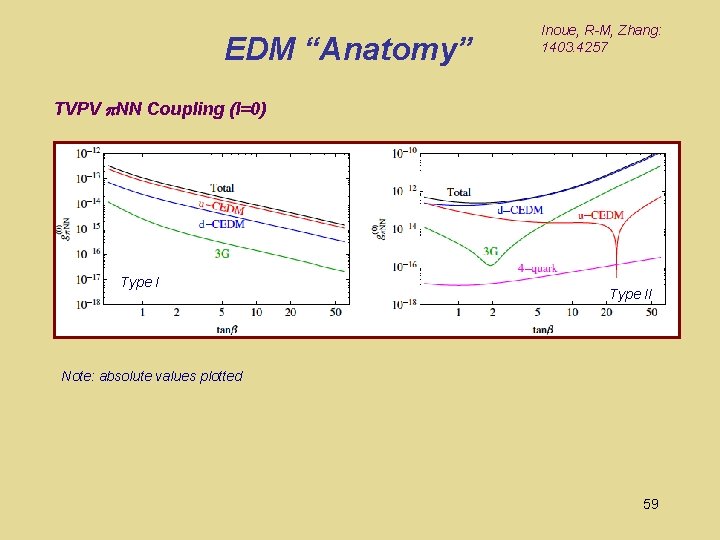
EDM “Anatomy” Inoue, R-M, Zhang: 1403. 4257 TVPV p. NN Coupling (I=0) Type II Note: absolute values plotted 59

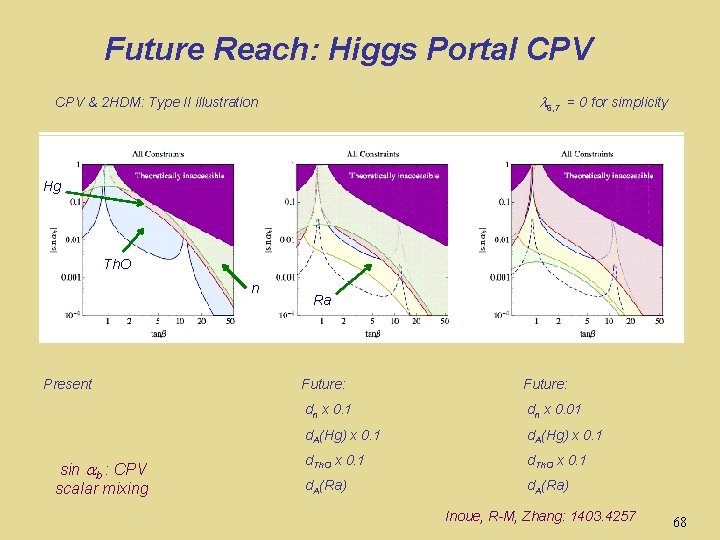
Future Reach: Higgs Portal CPV 6, 7 = 0 for simplicity CPV & 2 HDM: Type II illustration Hg Th. O n Present sin b : CPV scalar mixing Ra Future: dn x 0. 1 dn x 0. 01 d. A(Hg) x 0. 1 d. Th. O x 0. 1 d. A(Ra) Inoue, R-M, Zhang: 1403. 4257 68

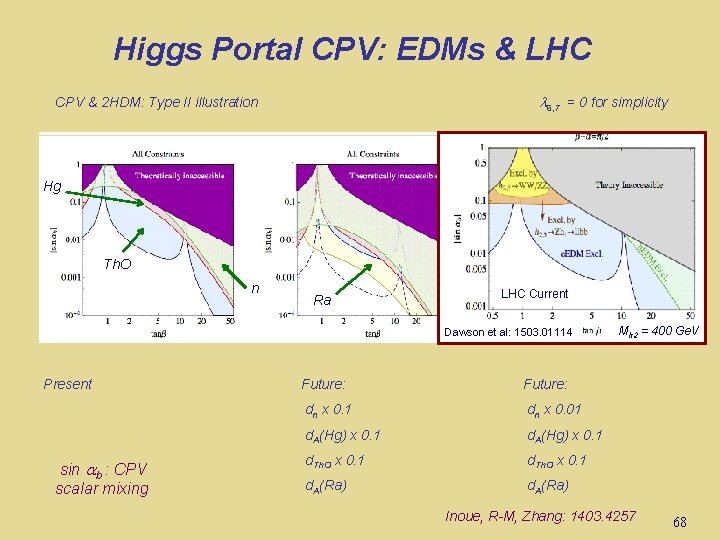
Higgs Portal CPV: EDMs & LHC 6, 7 = 0 for simplicity CPV & 2 HDM: Type II illustration Hg Th. O n Ra LHC Current Dawson et al: 1503. 01114 Present sin b : CPV scalar mixing Future: dn x 0. 1 dn x 0. 01 d. A(Hg) x 0. 1 d. Th. O x 0. 1 d. A(Ra) Mh 2 = 400 Ge. V Inoue, R-M, Zhang: 1403. 4257 68

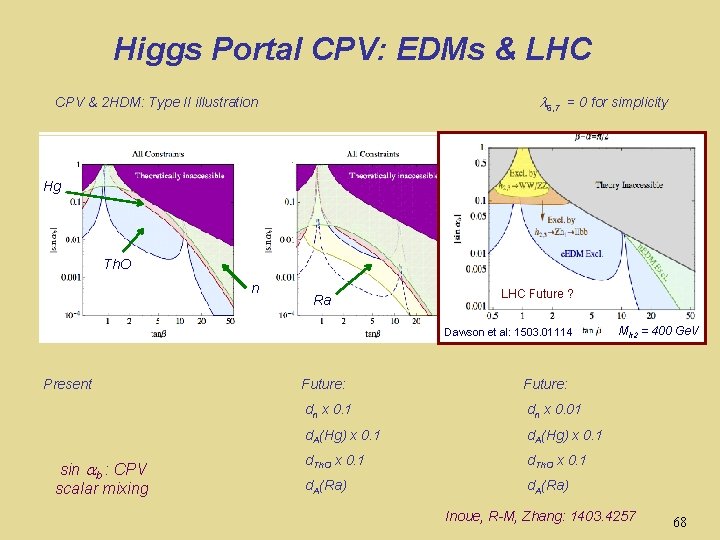
Higgs Portal CPV: EDMs & LHC 6, 7 = 0 for simplicity CPV & 2 HDM: Type II illustration Hg Th. O n Ra LHC Future ? Dawson et al: 1503. 01114 Present sin b : CPV scalar mixing Future: dn x 0. 1 dn x 0. 01 d. A(Hg) x 0. 1 d. Th. O x 0. 1 d. A(Ra) Mh 2 = 400 Ge. V Inoue, R-M, Zhang: 1403. 4257 68

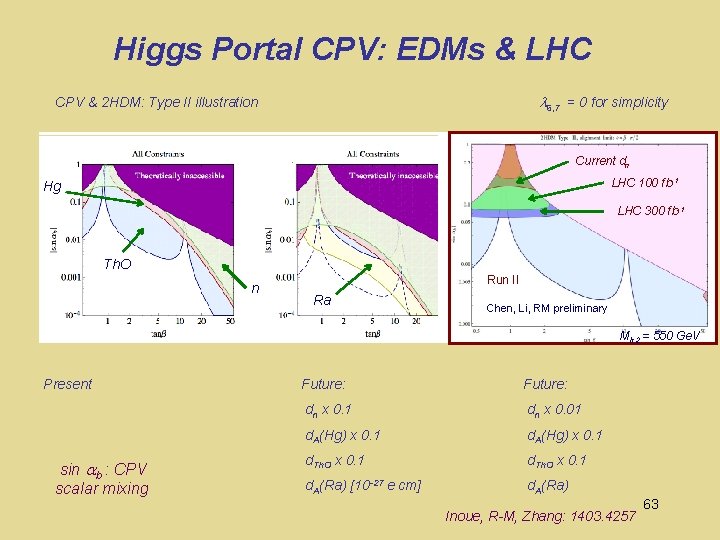
Higgs Portal CPV: EDMs & LHC 6, 7 = 0 for simplicity CPV & 2 HDM: Type II illustration Current dn LHC 100 fb-1 Hg LHC 300 fb-1 Th. O n Run II Ra Chen, Li, RM preliminary Mh 2 = 550 Ge. V Present sin b : CPV scalar mixing Future: dn x 0. 1 dn x 0. 01 d. A(Hg) x 0. 1 d. Th. O x 0. 1 d. A(Ra) [10 -27 e cm] d. A(Ra) Inoue, R-M, Zhang: 1403. 4257 63

Low-Energy / High-Energy Interplay Discovery “Diagnostic” ? Low energy High energy 64

V. Left-Right Symmetric Model 65

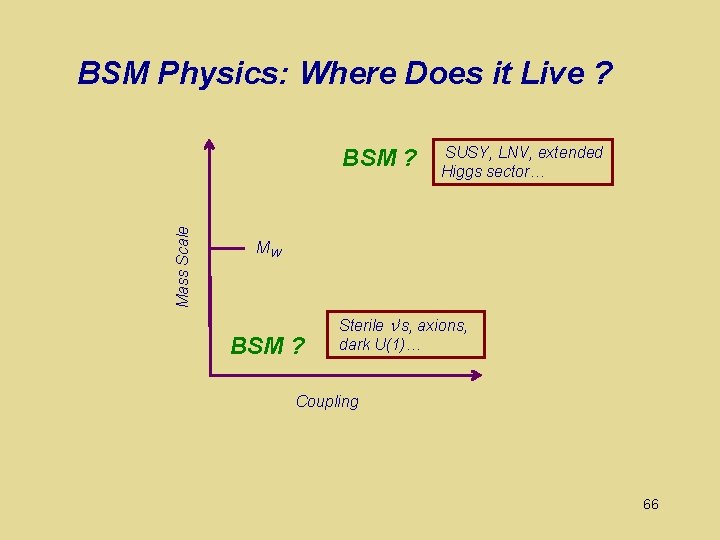
BSM Physics: Where Does it Live ? Mass Scale BSM ? SUSY, LNV, extended Higgs sector… MW BSM ? Sterile ’s, axions, dark U(1)… Coupling 66

Energy Scale BSM Mass Scale Parity Breaking Scale ~ MWR ? Weak Scale ~ MWL 67

Energy Scale Left-Right Symmetric Model Parity Breaking Scale ~ MWR ? Weak Scale ~ MWL SU(2)L x SU(2)R x U(1)B-L 68

Left-Right Symmetric Model Energy Scale See-saw scale ? Parity Breaking Scale ~ MWR ? Weak Scale ~ MWL SU(2)L x SU(2)R x U(1)B-L 69

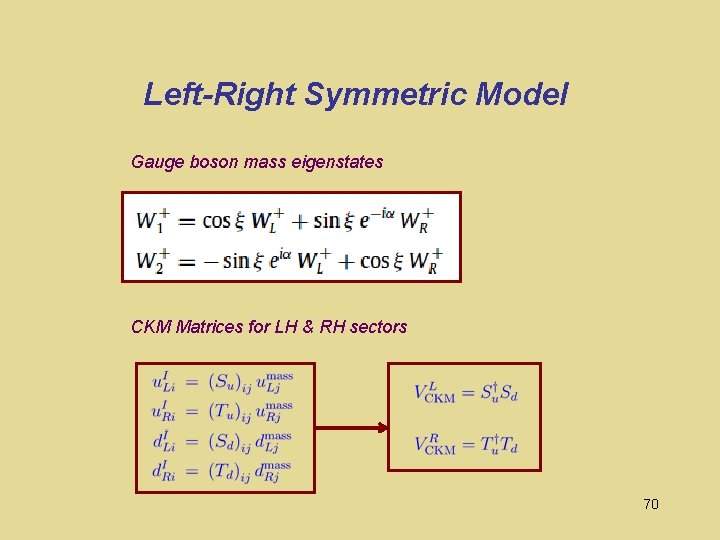
Left-Right Symmetric Model Gauge boson mass eigenstates CKM Matrices for LH & RH sectors 70

Left-Right Symmetric Model Dimensionless EDM: LRSM: One loop 71

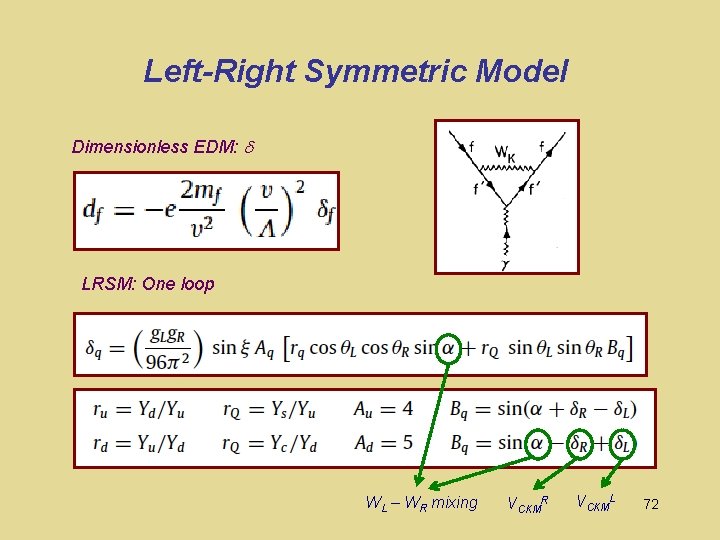
Left-Right Symmetric Model Dimensionless EDM: LRSM: One loop WL – WR mixing VCKMR VCKML 72

Left-Right Symmetric Model Dimensionless EDM: LRSM: One loop WL – WR mixing VCKMR VCKML 73

Left-Right Symmetric Model Dimensionless EDM: LRSM: Neutron 74

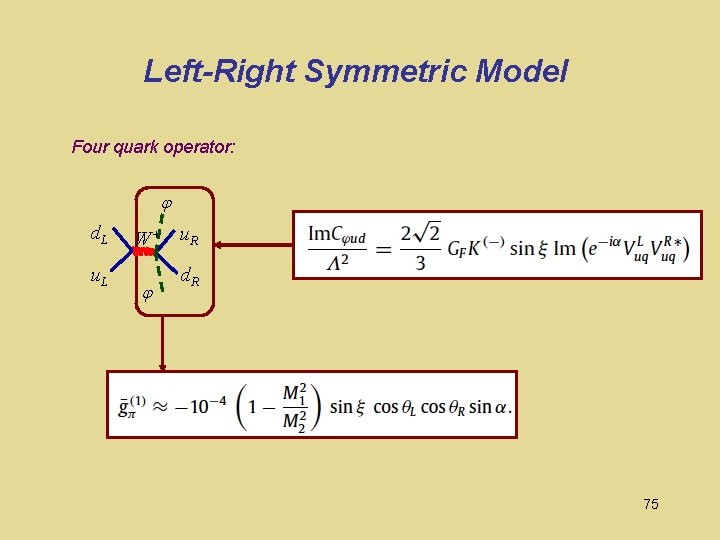
Left-Right Symmetric Model Four quark operator: d. L W+ u. R u. L d. R 75

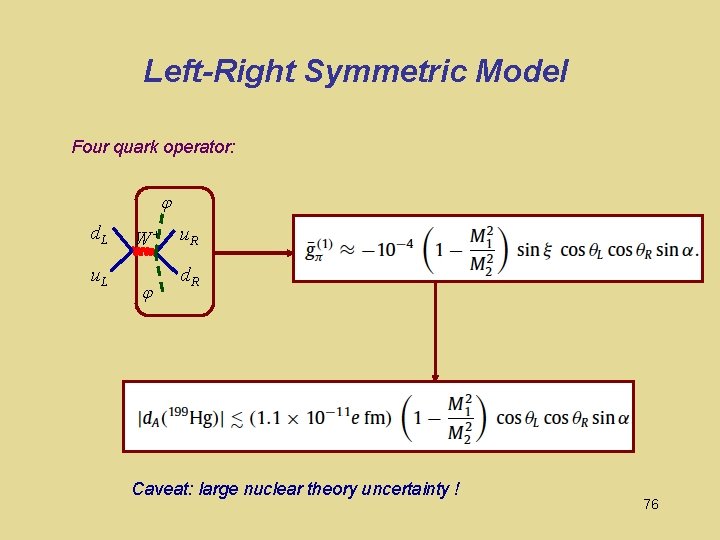
Left-Right Symmetric Model Four quark operator: d. L W+ u. R u. L d. R Caveat: large nuclear theory uncertainty ! 76

EDM Interpretation & Multiple Scales Collider Searches BSM CPV Early universe CPV SUSY, GUTs, Extra Dim… Particle spectrum; also scalars for baryon asym d= 6 Effective Operators: “CPV Sources” fermion EDM, quark chromo EDM, 3 gluon, 4 fermion QCD Matrix Elements Energy Scale Baryon Asymmetry Nuclear & atomic MEs dn , g NN , … Expt Schiff moment, other P- & T -odd moments, e-nucleus CPV 77

Wilson Coefficients: Summary f fermion EDM (3) q quark CEDM (2) CG~ 3 gluon (1) Cquqd non-leptonic (2) Clequ, ledq semi-leptonic (3) C ud induced 4 f (1) ~ 12 total + light flavors only (e, u, d) 78 78

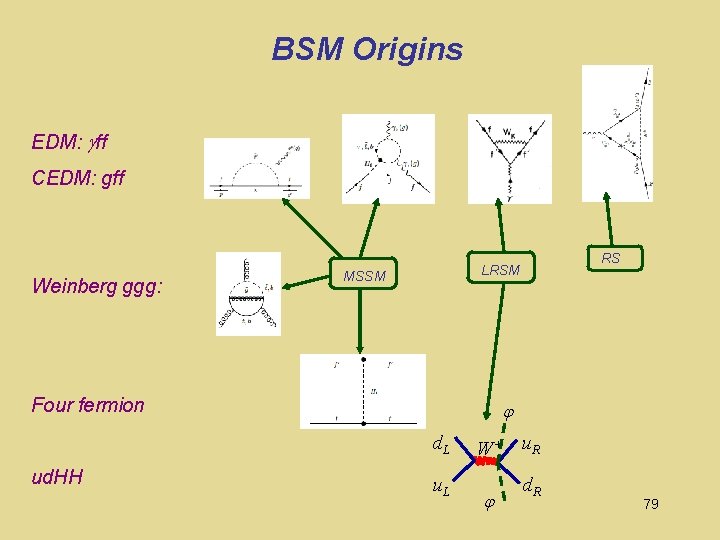
BSM Origins EDM: ff CEDM: gff Weinberg ggg: MSSM Four fermion ud. HH RS LRSM d. L W+ u. R u. L d. R 79

Back Up Slides 80

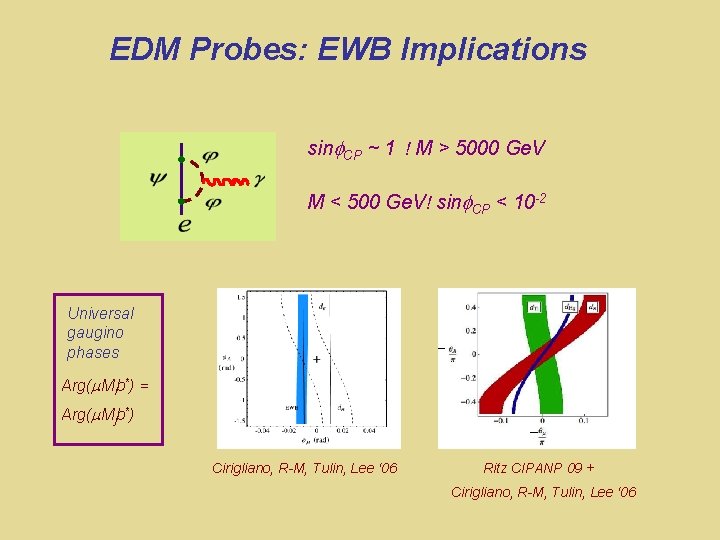
EDM Probes: EWB Implications sin CP ~ 1 ! M > 5000 Ge. V M < 500 Ge. V! sin CP < 10 -2 Universal gaugino phases Arg( Mib*) = Arg( Mjb*) Cirigliano, R-M, Tulin, Lee ‘ 06 Ritz CIPANP 09 + Cirigliano, R-M, Tulin, Lee ‘ 06

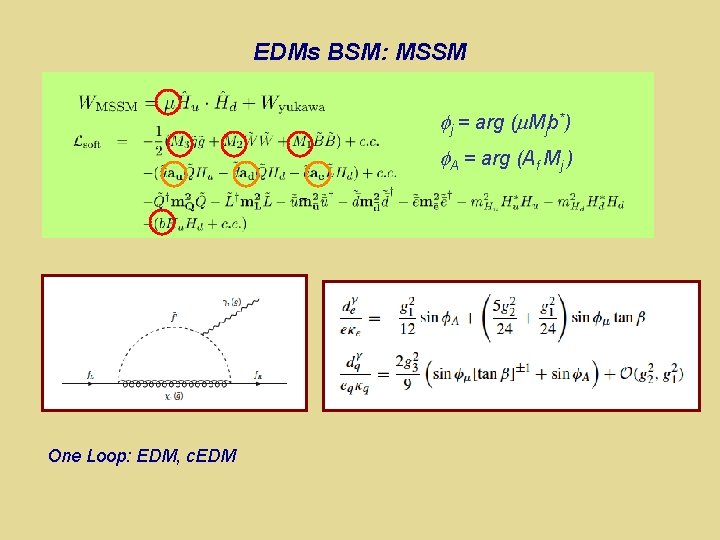
EDMs BSM: MSSM j = arg ( Mjb*) A = arg (Af Mj ) One Loop: EDM, c. EDM

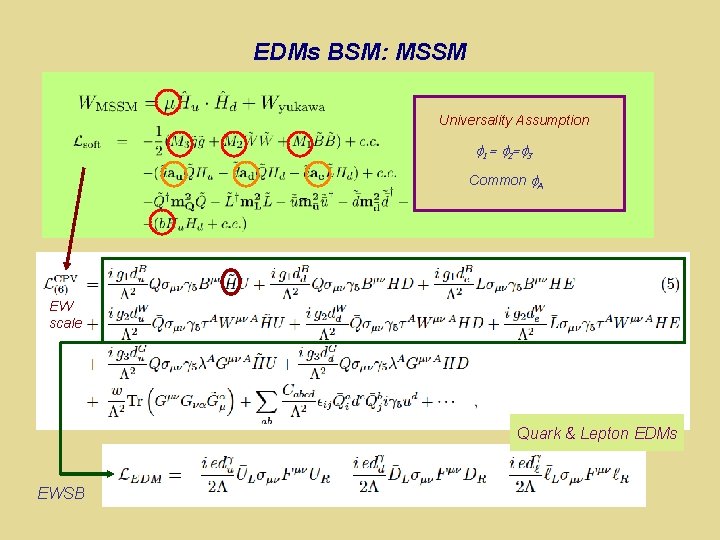
EDMs BSM: MSSM Universality = arg (Assumption M b*) j j A = arg (Af Mj ) Common A EW scale Quark & Lepton EDMs EWSB

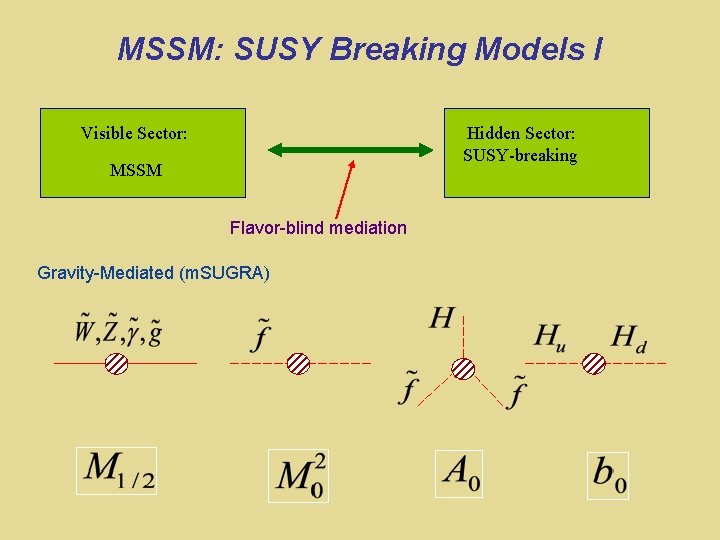
MSSM: SUSY Breaking Models I Visible Sector: Hidden Sector: SUSY-breaking MSSM Flavor-blind mediation Gravity-Mediated (m. SUGRA)

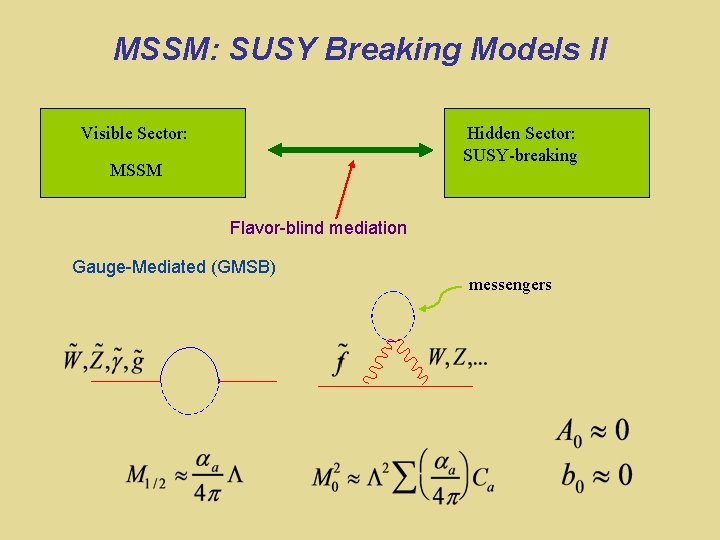
MSSM: SUSY Breaking Models II Visible Sector: Hidden Sector: SUSY-breaking MSSM Flavor-blind mediation Gauge-Mediated (GMSB) messengers

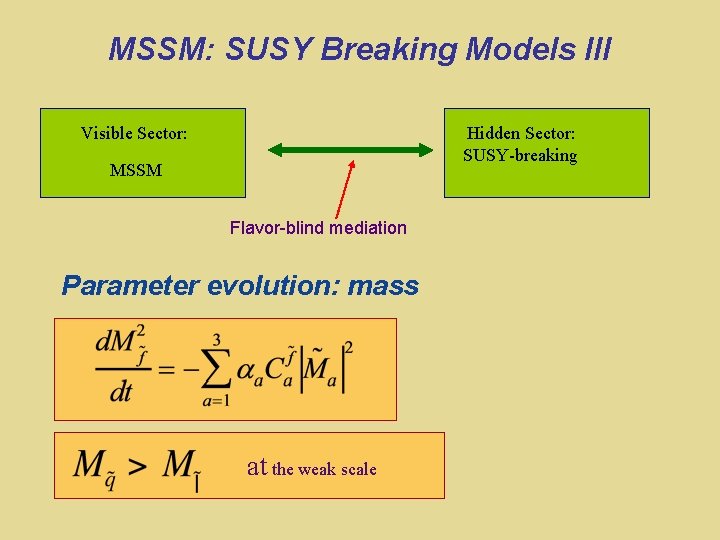
MSSM: SUSY Breaking Models III Visible Sector: Hidden Sector: SUSY-breaking MSSM Flavor-blind mediation Parameter evolution: mass at the weak scale

GF & the “hierarchy problem” SUSY Relation: Quadratic divergence ~ UV 2 cancels After EWSB:

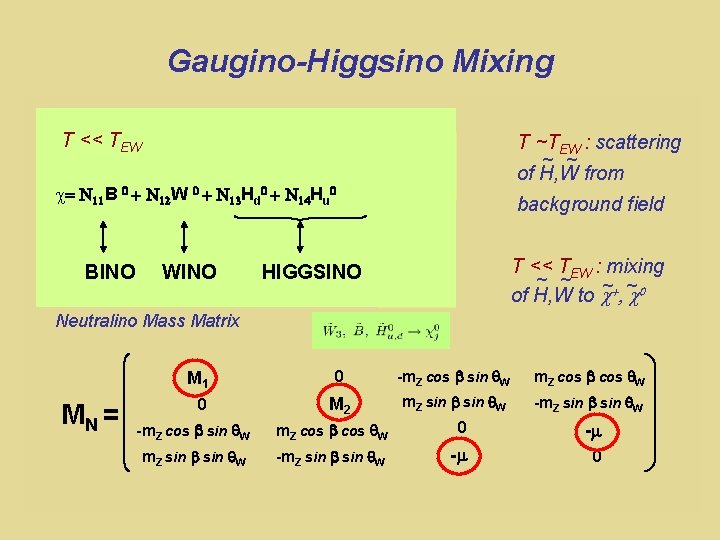
Gaugino-Higgsino Mixing Chargino Mass Matrix T << TEW c= N 11 B 0+ MC = BINO T ~TEW : scattering ~ ~ of H, W from CPV 0 N 12 W + N 13 Hd 0 + N 14 Hu 0 M 2 WINO background field m T << TEW : mixing ~ ~ ~0 of H, W to c~+, c HIGGSINO Neutralino Mass Matrix M 1 MN = 0 0 -m. Z cos b sin q. W m. Z cos b cos q. W M 2 m. Z sin b sin q. W -m. Z cos b sin q. W m. Z cos b cos q. W 0 -m m. Z sin b sin q. W -m 0

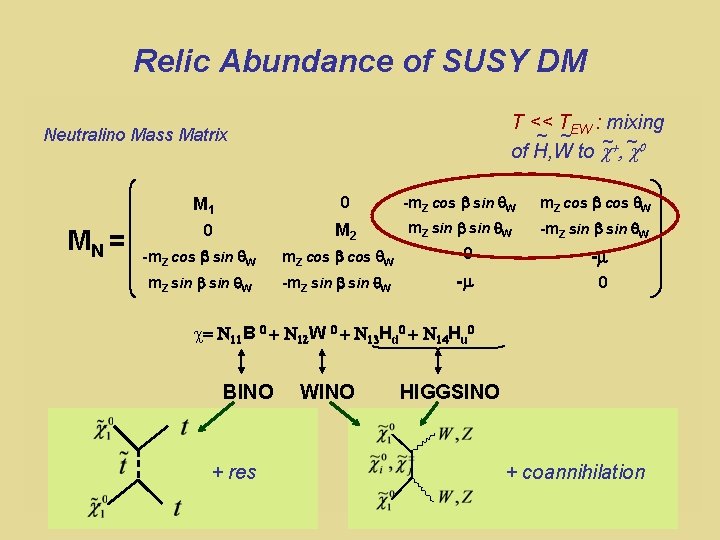
Relic Abundance of SUSY DM T << TEW : mixing ~ ~ ~0 of H, W to c~+, c Neutralino Mass Matrix M 1 MN = 0 0 -m. Z cos b sin q. W m. Z cos b cos q. W M 2 m. Z sin b sin q. W -m. Z cos b sin q. W m. Z cos b cos q. W 0 -m m. Z sin b sin q. W -m 0 c= N 11 B 0 + N 12 W 0 + N 13 Hd 0 + N 14 Hu 0 BINO + res WINO HIGGSINO + coannihilation

Sfermion Mixing Sfermion mass matrix T ~TEW : scattering ~ ~ of f. L, f. R from background field T << TEW : mixing ~ ~ of f. L, f. R to f 1, f 2 Qf < 0 Qf > 0