Lecture VI Collective Behavior of Multi Agent Systems

Lecture VI: Collective Behavior of Multi. Agent Systems II: Intervention Zhixin Liu Complex Systems Research Center, Academy of Mathematics and Systems Sciences, CAS

In the last lecture, we talked about Collective Behavior of Multi-Agent Systems I: Analysis

In the last lecture, we talked about n n Introduction Model: Vicsek model

Multi-Agent System (MAS) l MAS l l l Autonomy: capable of autonomous action Interactions: capable of interacting with other agents Many agents Local interactions between agents Collective behavior in the population level l l More is different. ---Philp Anderson, 1972 e. g. , small-world, swarm intelligence, panic, phase transition, coordination, synchronization, consensus, clustering, aggregation, …… Examples: Physical systems Biological systems Social and economic systems Engineering systems ……

Vicsek Model (T. Vicsek et al. , PRL, 1995) http: //angel. elte. hu/~vicsek/ r A bird’s neighborhood Alignment: steer towards the average heading of neighbors xi(t) : position of agent i in the plane : heading of agent i v: the constant speed of birds r: radius of neighborhood
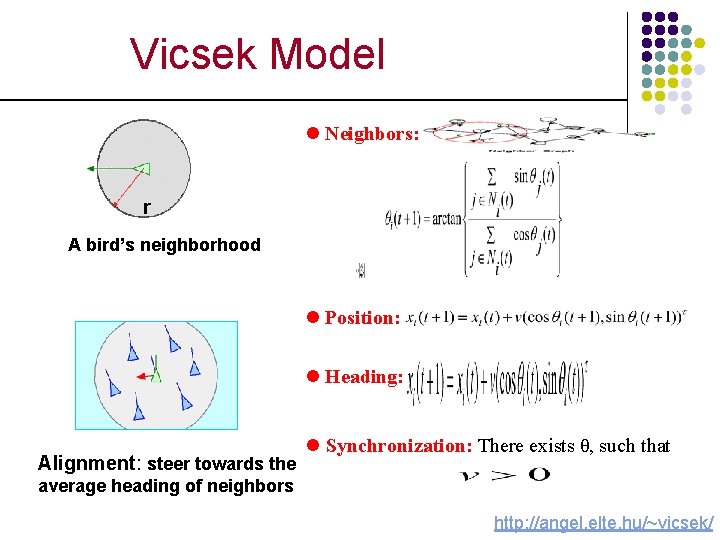
Vicsek Model l Neighbors: r A bird’s neighborhood l Position: l Heading: Alignment: steer towards the l Synchronization: There exists θ, such that average heading of neighbors http: //angel. elte. hu/~vicsek/

In the last lecture, we talked about n n Introduction Model Theoretical analysis Concluding remarks

The Linearized Vicsek Model A. Jadbabaie , J. Lin, and S. Morse, IEEE Trans. Auto. Control, 2003.

Theorem 2 (Jadbabaie et al. , 2003) Joint connectivity of the neighbor graphs on each time interval [th, (t+1)h] with h >0 Synchronization of the linearized Vicsek model Related result: J. N. Tsitsiklis, et al. , IEEE TAC, 1984

Random Framework Random initial states: 1) The initial positions of all agents are uniformly and independently distributed in the unit square; 2) The initial headings of all agents are uniformly and independently distributed in [- +ε, -ε] with ε∈ (0, ). The initial headings and positions are independent.

Theorem 7 High Density Implies Synchronization For any given system parameters and when the number of agnets n is large, the Vicsek model will synchronize almost surely. This theorem is consistent with the simulation result.

Theorem 8 High density with short distance interaction Let and the velocity satisfy Then for large population, the MAS will synchronize almost surely.

Three Categories of Research on Collective Behavior

Three Categories of Research on Collective Behavior l Analysis Given the local rules of the agents, what is the collective behavior of the overall system ? (Bottom Up) l Design Given the desired collective behavior, what are the local rules for agents ? (Top Down) l Intervention Given the local rule of the agents, how we intervene the collective behavior? J. Han, M. Li, L. guo, JSSC, 2006

Example 1: Synchronization r A bird’s Neighborhood Simulation Result Alignment: steer towards the average heading of neighbors Q: Under what conditions such a system can reach consensus?

Example 2: Escape Panic D. Helbing, et al. , Nature, Vol. 407, 2000 Normal, no panic Fire, panic

Three Categories of Research on Collective Behaviors l Analysis Given the local rules of the agents, what is the collective behavior of the overall system ? (Bottom Up) l Design Given the desired collective behavior, what are the local rules for agents ? (Top Down) l Intervention Given the local rule of the agents, how we intervene the collective behavior? J. Han, M. Li, L. guo, JSSC, 2006

Example 1: Formation control How we design the control law of each plane to maintain the form ?

Example 2: Swarm Intelligence (Marco Dorigo et al. , 2001 -2004) www. answers. com/topic/s-bot-mobile-robot

Example 3: Distributed Control in Boid Model Each agent is described by a double integrator (Newton's second law of motion ): where xi, vi and ui represent the position, velocity and the control input of the agent i. Goal: 1) Avoid collision 2) Alignment 3) Cohension What information can be used to design the controller? The position and velocity of neighbors R. Olfati-Saber, IEEE Trans. Auto. Control , 2006.
![Algorithm Controller design: where A=[aij(q)] is the adjacency matrix, (·) is the action function, Algorithm Controller design: where A=[aij(q)] is the adjacency matrix, (·) is the action function,](http://slidetodoc.com/presentation_image_h2/d790bf3a9700704d1083098102a0fb99/image-21.jpg)
Algorithm Controller design: where A=[aij(q)] is the adjacency matrix, (·) is the action function, isσ-norm, and Neighbor graph Theorem 1: If the neighbor graphs are connected at each time instant. Then 1) The group will form cohesion. 2) All agents asymptotically move with the same velocity. 3) No interagent collisions occur.

Three Categories of Research on Collective Behaviors l Analysis Given the local rules of the agents, what is the collective behavior of the overall system ? (Bottom Up) l Design Given the desired collective behavior, what are the local rules for agents ? (Top Down) l Intervention Given the local rule of the agents, how we intervene the collective behavior? J. Han, M. Li, L. guo, JSSC, 2006

Intervention Example 1: Can we guide the birds’ flight if we know how they fly ?

Example 2: Leadership by Numbers Couzin, et al. , Nature, Vol. 433, 2005 The larger the group is, the smaller the leaders are needed.

Example 3: Cockroach J. Halloy, et al. , Science, November 2007

III. Intervention Given the local rule of the agents, how we intervene the collective behavior? l The current control theory can not be applied directly, because l It is a many-body self-organized system. l The purpose of control aims to collective behavior. l Not allowed to change the local rules of the existing agents; l Distributed Control: special task of formation, l Pinning Control: Networked system, imposed controllers on selected nodes

Intervention Via Soft Control

Soft Control l The multi-agent system: l l l Many agents Each agent follows the local rules Autonomous, distributed Agents are connected, the local effect will affect the whole. From Jing Han’s PPT

Soft Control u(t) l an associate of a person selling y(t) goods or services or a political group, who pretends no association to the seller/group The “Control”: and assumes the air of an l No global parameter to adjust enthusiastic customer. l Not to change the local rule of the existing agents; l Put a few “shill” agents to guide (seduce) Shill: is controlled by us, not following the local rules, is treated as an ordinary agent by other ordinary agents The power of shill seems limited The ‘control’ is soft and seems weak l l From Jing Han’s PPT

Soft Control U(t) y(t) Key points: l l l Different from distributed control approach. Intervention to the distributed system Not to change the local rule of the existing agents Add one (or a few) special agent – called “shill” based on the system state information, to intervene the collective behavior; The “ shill” is controlled by us, but is treated as an ordinary agent by all other agents. Shill is not leader, not leader-follower type. Feedback intervention by shill(s). This page is very important! From Jing Han’s PPT

There Are Lots of Questions … l What is the purpose/task of control here? l Synchronization/consensus l Group connected / Dissolve a group l Turning (Minimal Circling) l Lead to a destination (in a shortest time) l Avoid hitting an object l Tracking l … In what degree we can control the shill? l How much information the shill can observe ? l … l (heading, position, speed, …) (positions, headings, …) From Jing Han’s PPT

A Case Study l Problem statement: System: A group of n agents with initial headings i(0) [0, ); l Goal: all agents move to the direction of eventually. l Soft control: Design one shill agent based on the agents’ state information. l l Assumptions: l l l The local rule about the ordinary agents is known The position x 0(t) and heading 0(t) of the spy can be controlled at any time step t The state information (headings and positions) of all ordinary agents are observable at any time step From Jing Han’s PPT

Vicsek Model l Neighbors: r A bird’s Neighborhood l Heading: l Position: Alignment: steer towards the l Synchronization: There exists θ, such that average heading of neighbors http: //angel. elte. hu/~vicsek/

A Case Study l Problem statement: l System: A group of n agents with initial headings i(0) [0, ); l Goal: all agents move to the direction of eventually. l Soft control: Design one shill agent based on the agents’ state information. l Assumptions: l The local rule about the ordinary agents is known l The position x 0(t) and heading 0(t) of the shill can be controlled at any time step t l The state information (headings and positions) of all ordinary agents are observable at any time step From Jing Han’s PPT

Control the Shill agent The Control Law u From Jing Han’s PPT

Control the Shill agent Theorem 4: For any initial headings and positions i(0) [0, ), xi(0) R 2, 1 i n, the update rule and the control law uβ will lead to the asymptotic synchronization of the group. It is possible to control the collective behavior of a group of agents by a shill. J. Han, M. Li, L. guo, JSSC, 2006

Simulation

An Alternative Control Law otherwise where Result: The control law ut will also lead to asymptotic synchronization of the group.

Simulations Switching between u and ur Control Law u

Remarks on Soft Control l It is not just for the above model Can be applied to other MAS , e. g. , l l l Panic in Crowd Evolution of Language Multi-player Game …… We need a theory for Soft Control ! “Add the special agent(s)” is just one way Should be other ways for different systems: l Remove agents l Put obstacle l …… From Jing Han’s PPT

Intervention Via Leader-Follower Model (LFM)

Example 1: Leadership by Numbers Couzin, et al. , Nature, Vol. 433, 2005 The larger the group is, the smaller the leaders are needed.

Leader-Follower Model Problem statement: l System: A group of n agents; l Goal: All agents move with the expected direction eventually. l Intervention by leaders: Add some information agents-called “leaders”, which move with the expected direction.

Leader-Follower Model Ordinary agents Information agents l Key points: l l Not to change the local rule of the existing agents. Add some (usually not very few) “information” agents – called “leaders”, to control or intervene the MAS; But the existing agents treated them as ordinary agents. The proportion of the leaders is controlled by us (If the number of leaders is small, then connectivity may not be guaranteed). Open-loop intervention by leaders.

Mathematical Model Ordinary agents (labeled by 1, 2, …, n): Neighbors: Position: Heading: Leader agents (labeled by Heading: Position: ):

Simulation Example N=1000

Q: How many leaders are required for consensus/synchronization?

Random Framework Assumption on the initial states 1) The initial positions of all agents are independently and uniformly distributed in the unit square. 2) The initial headings of the agents are uniformly and independently distributed in [-π, π), and the initial headings of the leaders are. The headings and the positions are mutually independent.

Some Notations Adjacency matrix: Degree matrix: Weighted adjacency matrix: Weighted degree matrix: Leader degree matrix: Average matrix: Weighted average matrix: If i ~ j Otherwise

Some Notations (cont. ) Laplacian : L(0)=D(0) – A(0) “Normalized Laplacian” : Spectrum : “Spectral gap”: where

Key Steps in the Analysis of the LFM Ø Analysis of the system dynamics Ø Estimation of the rate of consensus Ø Dealing with the matrices with increasing dimension Ø Dealing with the inherent nonlinearity

Analysis of the System Dynamics l Evolution of the distance Lemma 1: For any two agents i and j, their distance satisfy the following inequality: where is important for the evolution of the distance!

Analysis of the System Dynamics l Evolution of the headings Step 1: Projection

Analysis of the System Dynamics Step 2: Analyze the stability of where Step 3: Dealing with the changing neighbor graphs

Estimation of Consensus Rate The consensus rate depends on 1) A key lemma: For any vector f=[f 1, f 2, …, fn]τ, we have 2)

Dealing with the Matrices with Increasing Dimension Estimation of multi-array martingales where Moreover, if then we have

Dealing with the Matrices with Increasing Dimension Using the above corollary, we have for large n where

The Degree of The Initial Graph Lemma: For initial graph G 0, we have for large n

The Degree of The Initial Graph Corollary:

Dealing with the Inherent Nonlinearity Proposition 1 For any positive v and r, we have for large n where

Main Result Theorem 5 Let the velocity v > 0 and radius r > 0 be positive constants. If the proportion of the leaders satisfies where C is a constant depending on v and r, then the headings of all agents will converge to almost surely when the population size n is large enough.

Concluding Remarks l In this talk, we talked about intervention to the multi-agent systems: Ø Soft control Design the control law of the “shill” Ø Leader-follower model Control the number of the leaders

Concluding Remarks These two lectures mainly focus on the collective behavior of the MAS. In the next lecture, we will talk about game theory.

Thank you!
- Slides: 64