Lecture Presentation Chapter 2 The Metric System John

Lecture Presentation Chapter 2 The Metric System John Singer Jackson College © 2018 Pearson Education, Inc.

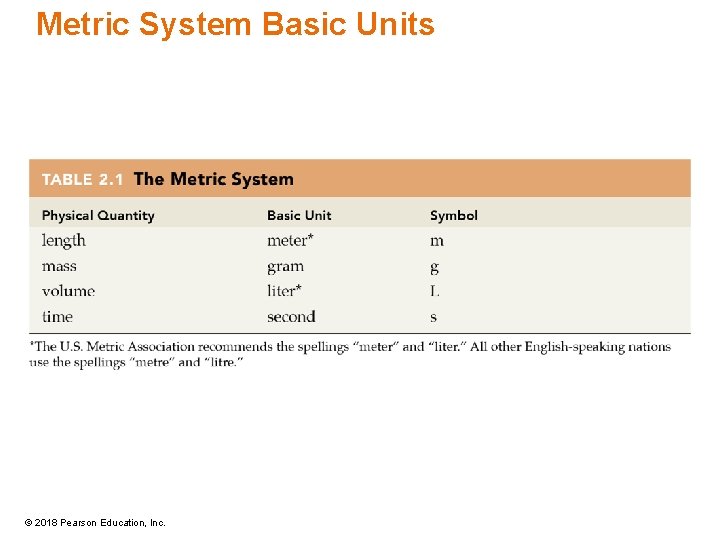
Basic Units and Symbols • The English system was used primarily in the British Empire. • The French organized a committee to devise a universal measuring system. • After about 10 years, the committee designed and agreed on the metric system. • The metric system offers simplicity with a single base unit for each measurement. © 2018 Pearson Education, Inc.

Metric System Basic Units © 2018 Pearson Education, Inc.

Original Metric Unit Definitions • A meter was defined as 1/10, 000 of the distance from the North Pole to the equator. • A kilogram (1000 grams) was equal to the mass of a cube of water measuring 0. 1 m on each side. • A liter was set equal to the volume of one kilogram of water at 4 °C. © 2018 Pearson Education, Inc.

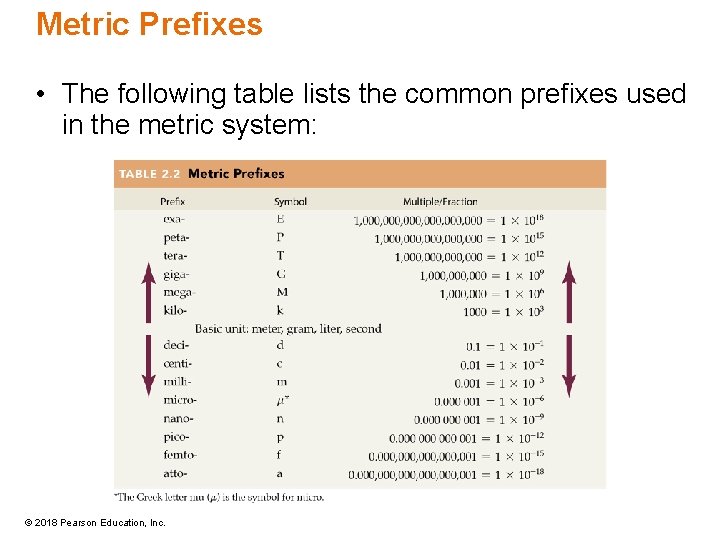
Metric Prefixes • The following table lists the common prefixes used in the metric system: © 2018 Pearson Education, Inc.

Metric Symbols • The names of metric units are abbreviated using symbols. Use the prefix symbol followed by the symbol for the base unit: – Kilometer is abbreviated km. – Milligram is abbreviated mg. – Microliter is abbreviated m. L. – Nanosecond is abbreviated ns. © 2018 Pearson Education, Inc.

Critical Thinking: The International System of Units (SI) • An advantage of the metric system (i. e. , International System of Units, SI) is that it is a decimal system. • It uses prefixes to enlarge or reduce the basic units. • For example: – A kilometer is 1000 meters. – A millimeter is 1/1000 of a meter. © 2018 Pearson Education, Inc.

Metric Conversion Factors • A unit equation relates two quantities that are equal. • For example: – 1 kilometer = 1000 meters – 1 km = 1000 m • Also, we can write: – 1 centimeter = 1/100 of a meter or – 100 cm = 1 m © 2018 Pearson Education, Inc.

Unit Factors • A unit conversion factor, or unit factor, is a ratio of two equivalent quantities. • For the unit equation 1 m = 100 cm, we can write two unit factors: 1 m 100 cm © 2018 Pearson Education, Inc. or 100 cm 1 m

Metric–Metric Conversions • An effective method for solving problems in science is the unit analysis method. • It is also often called dimensional analysis or the factor-label method. © 2018 Pearson Education, Inc.

Applying the Unit Analysis Method • Step 1: Write down the unit asked for in the answer. • Step 2: Write down the given value related to the answer. • Step 3: Apply unit factor(s) to convert the unit in the given value to the unit in the answer. © 2018 Pearson Education, Inc.

Metric–Metric Conversion Problem What is the mass in grams of a 325 -mg aspirin tablet? • Step 1: We want grams. • Step 2: We write down the given: 325 mg. • Step 3: We apply a unit factor (1000 mg = 1 g) and round to three significant figures. 1 g 325 mg × = 0. 325 g 1000 mg © 2018 Pearson Education, Inc.

Two Metric–Metric Conversions A hospital has 125 deciliters of blood plasma. What is the volume in milliliters? • Step 1: We want the answer in m. L. • Step 2: We have 125 d. L. • Step 3: We need to first convert d. L to L and then convert L to m. L: 1 L and 1000 m. L 10 d. L 1 L © 2018 Pearson Education, Inc.

Two Metric–Metric Conversions • In working a problem where there is not a direct conversion from the given unit to the desired unit, first convert to the metric unit with no prefix. • Apply both unit factors, and round the answer to three significant digits. • Notice that both d. L and L units cancel, leaving us with units of m. L. 1 L 1000 m. L × 125 d. L × = 12, 500 m. L 10 d. L 1 L © 2018 Pearson Education, Inc.

Another Example The mass of the Earth’s moon is 7. 35 × 1022 kg. What is the mass expressed in nanograms, ng? • We want ng; we have 7. 35 × 1022 kg. • Convert kilograms to grams, and then grams to nanograms. 6 ng 1000 g 1 × 10 × 7. 35 × 1022 kg × = 7. 35 × 1031 ng 1 kg 1 g © 2018 Pearson Education, Inc.

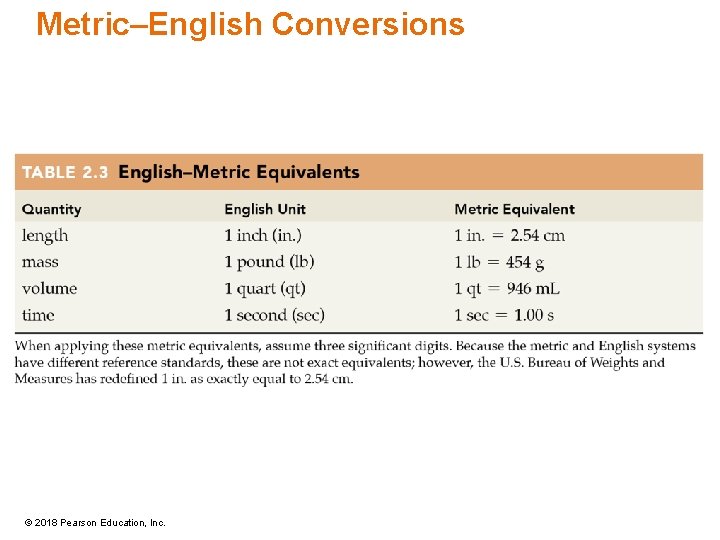
Metric–English Conversions • The English system is still very common in the United States. • We often have to convert between English and metric units. © 2018 Pearson Education, Inc.

Metric–English Conversions © 2018 Pearson Education, Inc.

Metric–English Conversions The length of an American football field, including the end zones, is 120 yards. What is the length in meters? • Convert 120 yd to meters (given that 1 yd = 0. 914 m). 0. 914 m 120 yd × = 110 m 1 yd © 2018 Pearson Education, Inc.

Metric–English Conversions A half-gallon carton contains 64. 0 fl oz of milk. How many milliliters of milk are in a carton? • We want m. L; we have 64. 0 fl oz. • Use 1 qt = 32 fl oz, and 1 qt = 946 m. L. 1 qt 946 m. L 64. 0 fl oz × × = 1, 890 m. L 32 fl oz 1 qt © 2018 Pearson Education, Inc.

Another English–Metric Problem A marathon is 26. 2 miles. What is the distance in kilometers (1 km = 0. 62 mi)? • Step 1: We want km. • Step 2: We write down the given: 26. 2 mi. • Step 3: We apply a unit factor (1 km = 0. 62 mi) and round to three significant figures. © 2018 Pearson Education, Inc.

Compound Units • Some measurements have a ratio of units. • For example, the speed limit on many highways is 55 miles per hour. How would you convert this to meters per second? • Convert one unit at a time using unit factors. 1. First, miles meters 2. Next, hours seconds © 2018 Pearson Education, Inc.

Compound Unit Problem A motorcycle is traveling at 105 km/h. What is the speed in meters per second? • We have km/h; we want m/s. • Use 1 km = 1000 m and 1 h = 3600 s. 105 km 1000 m 1 h × × = 29. 2 m/s 1 km h 3600 s © 2018 Pearson Education, Inc.

Critical Thinking: World Trade Center • When discussing measurements, it is critical that we use the proper units. • The World Trade Center footprint was 150 feet square, not 150 square feet. • NASA engineers mixed metric and English units when designing the Mars Climate Orbiter. – The engineers used kilometers rather than miles. – The spacecraft approached too close to the Martian surface and burned up in the atmosphere. © 2018 Pearson Education, Inc.

The Percent Concept • A percent (%) expresses the amount of a single quantity compared to an entire sample. • A percent is a ratio of parts per 100 parts. • The formula for calculating percent is shown below: © 2018 Pearson Education, Inc.

Calculating Percentages • Bronze is an alloy of copper and tin. If a sample of bronze contains 79. 2 g of copper and 10. 8 g of tin, what is the percent of copper in bronze? 79. 2 g × 100% = 88. 0% (79. 2 + 10. 8) g © 2018 Pearson Education, Inc.

Percent Unit Factors • A percent can be expressed as parts per 100 parts. • 25% can be expressed as 25/100, and 10% can be expressed as 10/100. • We can use a percent expressed as a ratio as a unit factor. – A rock is 4. 70% iron, so © 2018 Pearson Education, Inc.

Percent Unit Factor Calculation The Earth and Moon have a similar composition; each contains 4. 70% iron. What is the mass of iron in a lunar sample that weighs 92 g? • Step 1: We want g iron. • Step 2: We write down the given: 92 g sample. • Step 3: We apply a unit factor (4. 70 g iron = 100 g sample) and round to three significant figures. © 2018 Pearson Education, Inc.

Volume by Calculation • The volume of an object is calculated by multiplying the length (l) times the width (w) times the thickness (t). volume = l × w × t • All three measurements must be in the same units. • If an object measures 3 cm by 2 cm by 1 cm, the volume is 6 cm 3 (cm 3 is cubic centimeters). © 2018 Pearson Education, Inc.

Volumes of Solids, Liquids, and Gases • The liter (L) is the basic unit of volume in the metric system. • One liter is defined as the volume occupied by a cube that is 10 cm on each side. © 2018 Pearson Education, Inc.

Volumes of Solids, Liquids, and Gases • 1 liter is equal to 1000 cubic centimeters. – 10 cm × 10 cm = 1000 cm 3 • 1000 cm 3 = 1 L = 1000 m. L • Therefore, 1 cm 3 = 1 m. L © 2018 Pearson Education, Inc.

Cubic-Liquid Volume Conversion An automobile engine displaces a volume of 498 cm 3 in each cylinder. What is the displacement of a cylinder in cubic inches (in 3)? • We want in 3; we have 498 cm 3. • Use 1 in = 2. 54 cm three times. 498 cm 3 1 in × × × = 30. 4 in 3 2. 54 cm © 2018 Pearson Education, Inc.

Volume by Displacement • If a solid has an irregular shape, its volume cannot be determined by measuring its dimensions. • You can determine its volume indirectly by measuring the amount of water it displaces. • This technique is called volume by displacement. • Volume by displacement can also be used to determine the volume of a gas, as long as the gas is not soluble in water. © 2018 Pearson Education, Inc.

Solid Volume by Displacement You want to measure the volume of an irregularly shaped piece of jade. • Partially fill a volumetric flask with water and measure the volume of the water. • Add the jade, and measure the difference in volume. • The volume of the jade is 10. 5 m. L. © 2018 Pearson Education, Inc.

Gas Volume by Displacement You want to measure the volume of gas given off in a chemical reaction. • The gas produced displaces the water in the flask into the beaker. The volume of water displaced is equal to the volume of gas. © 2018 Pearson Education, Inc.

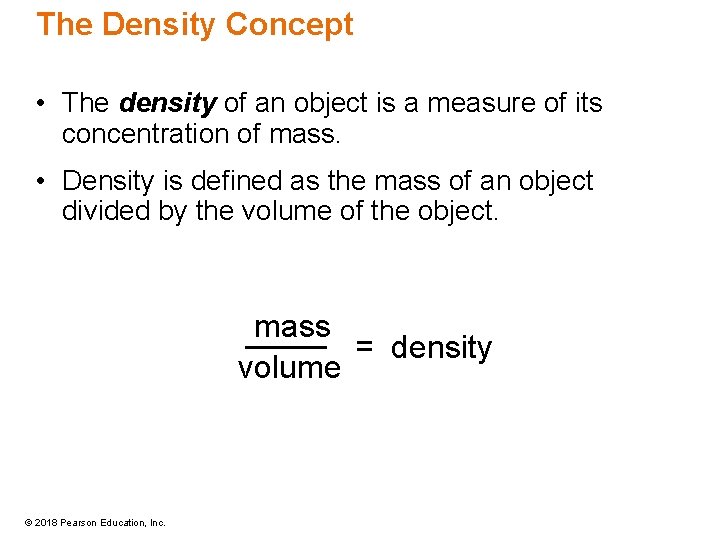
The Density Concept • The density of an object is a measure of its concentration of mass. • Density is defined as the mass of an object divided by the volume of the object. mass = density volume © 2018 Pearson Education, Inc.

Density • Density is expressed in different units. It is usually grams per milliliter (g/m. L) for liquids, grams per cubic centimeter (g/cm 3) for solids, and grams per liter (g/L) for gases. © 2018 Pearson Education, Inc.

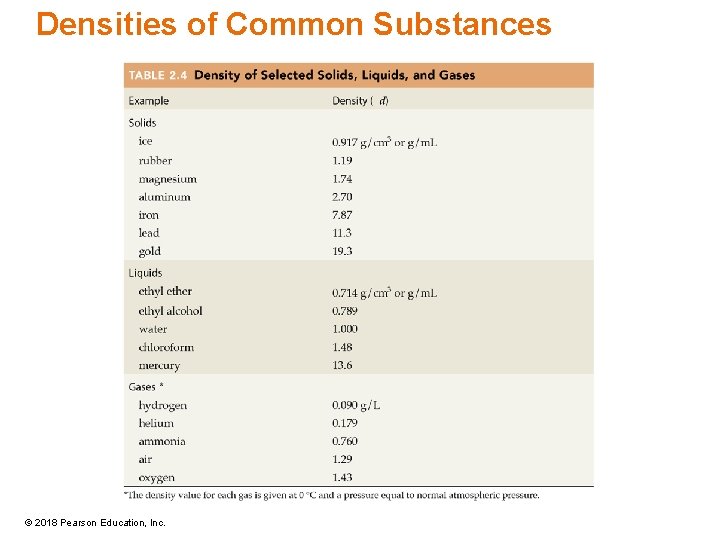
Densities of Common Substances © 2018 Pearson Education, Inc.

Estimating Density • We can estimate the density of a substance by comparing it to another object. • A solid object will float on top of a liquid with a higher density. • Object S 1 has a density less than that of water, but larger than that of L 1. • Object S 2 has a density less than that of L 2, but larger than that of water. © 2018 Pearson Education, Inc.

Calculating Density What is the density of a platinum nugget that has a mass of 224. 50 g and a volume of 10. 0 cm 3 ? Recall, density is mass/volume. 224. 50 g 3 = 22. 5 g/cm 10. 0 cm 3 © 2018 Pearson Education, Inc.

Density as a Unit Factor • We can use density as a unit factor for conversions between mass and volume. • An automobile battery contains 1275 m. L of acid. If the density of battery acid is 1. 84 g/m. L, how many grams of acid are in an automobile battery? – We have 1275 m. L; we want grams: 1. 84 g 1275 m. L × = 2350 g m. L © 2018 Pearson Education, Inc.

Temperature • Temperature is a measure of the average kinetic energy of individual particles in motion. • There are three temperature scales: 1. Fahrenheit 2. Celsius 3. Kelvin • Kelvin is the absolute temperature scale. © 2018 Pearson Education, Inc.

Temperature Scales • On the Fahrenheit scale, water freezes at 32 °F and boils at 212 °F. • On the Celsius scale, water freezes at 0 °C and boils at 100 °C. These are the reference points for the Celsius scale. • Water freezes at 273 K and boils at 373 K on the Kelvin scale. © 2018 Pearson Education, Inc.

Temperature Conversions • The relationship between the Fahrenheit and Celsius temperature scales is linear. Therefore this relationship can be represented in the standard format of an equation for a straight line. • This is the equation for converting °C to °F. © 2018 Pearson Education, Inc.

Temperature Scales • Solving the previous equation for °C leads to the following: This is the equation for converting °F to °C. © 2018 Pearson Education, Inc.

Temperature Scales • To convert from °C to K, add 273. °C + 273 = K © 2018 Pearson Education, Inc.

Fahrenheit–Celsius Conversions • Body temperature is 98. 6 °F. What is body temperature in degrees Celsius? In Kelvin? K = °C + 273 = 37. 0 °C + 273 = 310 K © 2018 Pearson Education, Inc.

The Heat Concept • Heat is a measure of total energy. • Temperature measures the average energy of particles in a system. • Heat is often expressed in terms of joules (J) or calories (cal). © 2018 Pearson Education, Inc.

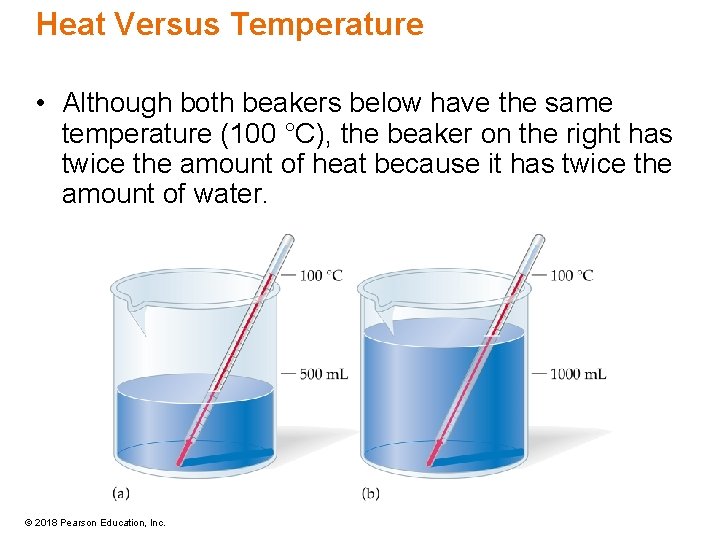
Heat Versus Temperature • Although both beakers below have the same temperature (100 °C), the beaker on the right has twice the amount of heat because it has twice the amount of water. © 2018 Pearson Education, Inc.

Specific Heat • The specific heat of a substance is the amount of heat required to raise the temperature of one gram of substance one degree Celsius. • It is expressed with units of calories per gram per degree Celsius. • The larger the specific heat, the more heat is required to raise the temperature of the substance. © 2018 Pearson Education, Inc.

Chapter Summary • The basic units in the metric system are grams for mass, liters for volume, and meters for distance. • The base units are modified using prefixes to reduce or enlarge the base units by factors of 10. • We can use unit factors to convert between metric units. • We can convert between metric and English units using unit factors. © 2018 Pearson Education, Inc.

Chapter Summary • A unit equation is a statement of two equivalent quantities. • A unit factor is a ratio of two equivalent quantities. • Unit factors can be used to convert measurements between different units. • A percent is the ratio of parts per 100 parts. © 2018 Pearson Education, Inc.

Chapter Summary • Volume is defined as length × width × thickness. • Volume can also be determined by displacement of water. • Density is mass divided by volume. © 2018 Pearson Education, Inc.

Chapter Summary, Continued • Temperature is a measure of the average energy of the particles in a sample. • Heat is a measure of the total energy of a substance. • Specific heat is a measure of how much heat is required to raise the temperature of a substance. © 2018 Pearson Education, Inc.