Lecture Power Points Chapter 8 Physics Principles with

Lecture Power. Points Chapter 8 Physics: Principles with Applications, 7 th edition Giancoli © 2014 Pearson Education, Inc. This work is protected by United States copyright laws and is provided solely for the use of instructors in teaching their courses and assessing student learning. Dissemination or sale of any part of this work (including on the World Wide Web) will destroy the integrity of the work and is not permitted. The work and materials from it should never be made available to students except by instructors using the accompanying text in their classes. All recipients of this work are expected to abide by these restrictions and to honor the intended pedagogical purposes and the needs of other instructors who rely on these materials.

Chapter 8 Rotational Motion © 2014 Pearson Education, Inc.

Contents of Chapter 8 • Center of Mass • Angular Quantities • Constant Angular Acceleration • Rolling Motion (Without Slipping) • Torque • Rotational Dynamics; Torque and Rotational Inertia • Solving Problems in Rotational Dynamics • Rotational Kinetic Energy • Angular Momentum and Its Conservation © 2014 Pearson Education, Inc.

7 -8 Center of Mass In (a), the diver’s motion is pure translation; in (b) it is translation plus rotation. There is one point that moves in the same path a particle would take if subjected to the same force as the diver. This point is called the center of mass (CM). © 2014 Pearson Education, Inc.

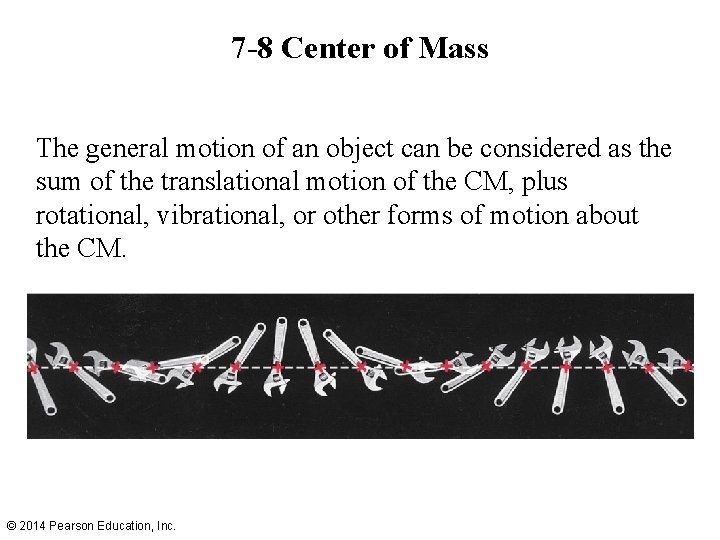
7 -8 Center of Mass The general motion of an object can be considered as the sum of the translational motion of the CM, plus rotational, vibrational, or other forms of motion about the CM. © 2014 Pearson Education, Inc.

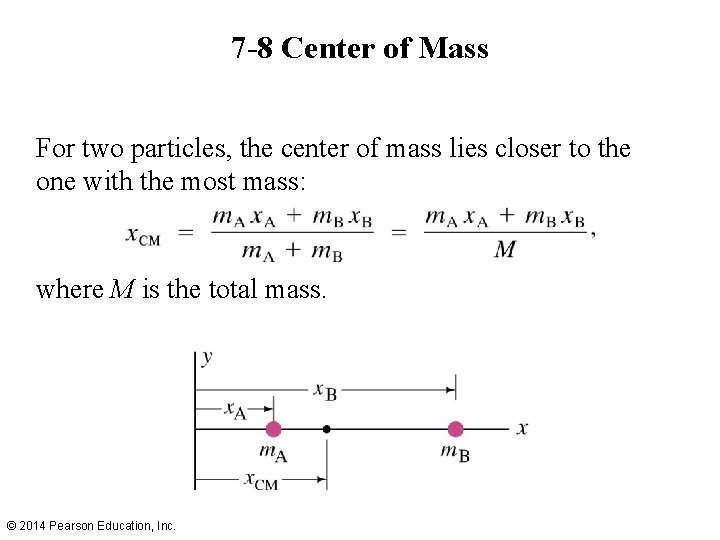
7 -8 Center of Mass For two particles, the center of mass lies closer to the one with the most mass: where M is the total mass. © 2014 Pearson Education, Inc.

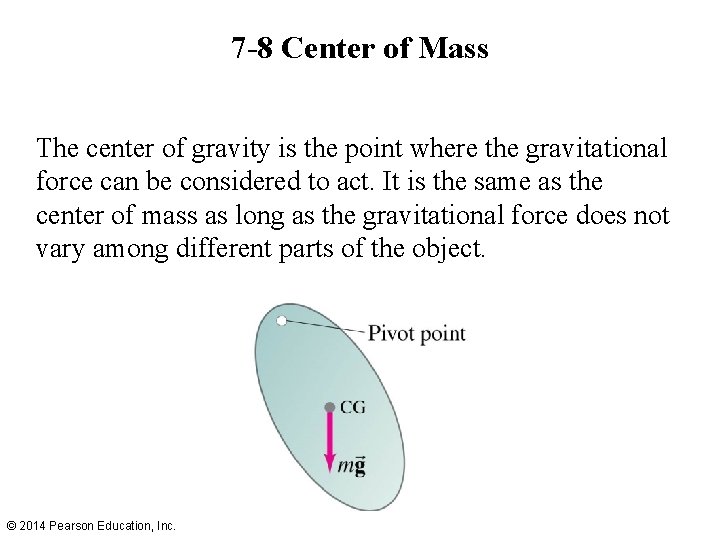
7 -8 Center of Mass The center of gravity is the point where the gravitational force can be considered to act. It is the same as the center of mass as long as the gravitational force does not vary among different parts of the object. © 2014 Pearson Education, Inc.

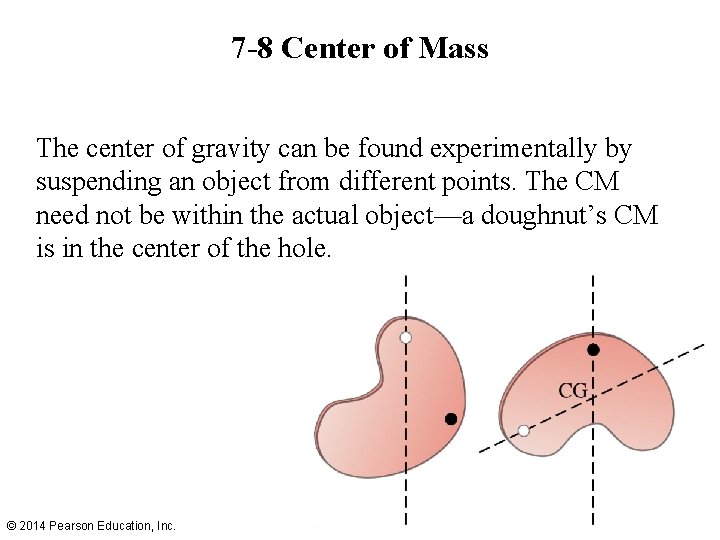
7 -8 Center of Mass The center of gravity can be found experimentally by suspending an object from different points. The CM need not be within the actual object—a doughnut’s CM is in the center of the hole. © 2014 Pearson Education, Inc.

Example 11 Three people of roughly equivalent mass, m, on a lightweight banana boat sit along the –axis at position x 1 =1. 0 m, x 2 =5. 0 m, and x 3 =6. 0 m. Find the position of the CM. Given: x 1 =1. 0 m, x 2 =5. 0 m, x 3 =6. 0 m. Formula: xcm= maxa + mbxb + mcxc ma+mb+mc Substitution: xcm = 1 m +5 m+6 m 3 Answer w/unit: 4. 00 m

8 -1 Angular Quantities In purely rotational motion, all points on the object move in circles around the axis of rotation (“O”). The radius of the circle is r. All points on a straight line drawn through the axis move through the same angle in the same time. The angle θ in radians is defined: (8 -1 a) where l is the arc length. © 2014 Pearson Education, Inc.

Example 8 -1 A bike wheel rotates 4. 50 revolutions. How many radians has it rotated? Given: 4. 50 revs Approach: Convert from revolutions to radians. 1 rev = 2πrad Substitution: 4. 50 rev x 2πrad 1 rev Answer w/unit: 28. 3 rad

Example 8 -2 A particular bird’s eye can just distinguish objects that subtend an angle no smaller than about 3 x 10 -4 rad. a) How many degrees is this? Given: Ɵ= 3 x 10 -4 rad Approach: Convert from radians to degrees. 360º = 2πrad Substitution: 3 x 10 -4 rad x 360º 2πrad Answer w/unit: 0. 0172º

Example 8 -2 continues A particular bird’s eye can just distinguish objects that subtend an angle no smaller than about 3 x 10 -4 rad. b) How small an object can the bird just distinguish when flying at a height of 100 m? Given: r=100 m, Ɵ= 3 x 10 -4 rad Formula: Ɵ = l r Substitution: 3 x 10 -4 rad = l 100 m Answer w/unit: 0. 0300 m

8 -1 Angular Quantities Angular displacement: Δθ = θ 2 – θ 1 The average angular velocity is defined as the total angular displacement divided by time: (8 -2 a) The instantaneous angular velocity: (8 -2 b) © 2014 Pearson Education, Inc.

8 -1 Angular Quantities The angular acceleration is the rate at which the angular velocity changes with time: (8 -3 a) The instantaneous acceleration: (8 -3 b) © 2014 Pearson Education, Inc.

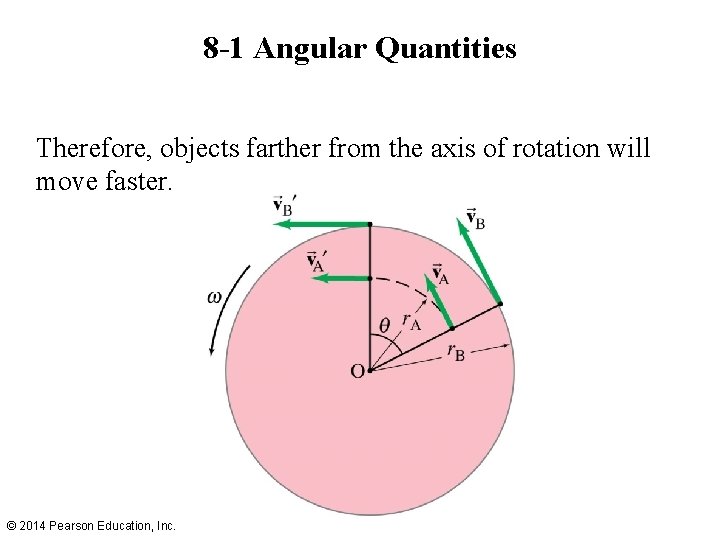
8 -1 Angular Quantities Every point on a rotating body has an angular velocity ω and a linear velocity v. They are related: (8 -4) © 2014 Pearson Education, Inc.

8 -1 Angular Quantities Therefore, objects farther from the axis of rotation will move faster. © 2014 Pearson Education, Inc.

Example 8 -3 On a rotating carousel or merry-goround, one child sits on a horse near the outer edge and another child sits on a lion halfway out from the center. a) Which child has the greater linear velocity? Answer: The linear velocity is the distance traveled divided by the time interval. In one rotation the child on the outer edge travels a longer distance than the child near the center, but the time interval is the same for both. Thus the child at the outer edge, on the horse, has the greater linear velocity.

Example 8 -3 continues On a rotating carousel or merry-goround, one child sits on a horse near the outer edge and another child sits on a lion halfway out from the center. b) Which child has the greater angular velocity? Answer: The angular velocity is the angle of rotation of the carousel as a whole divided by the time interval. For example, in one rotation both children rotate through the same angle (360º or 2πradians), The two children have the same angular velocity.

8 -1 Angular Quantities If the angular velocity of a rotating object changes, it has a tangential acceleration: (8 -5) Even if the angular velocity is constant, each point on the object has a centripetal acceleration: (8 -6) © 2014 Pearson Education, Inc.

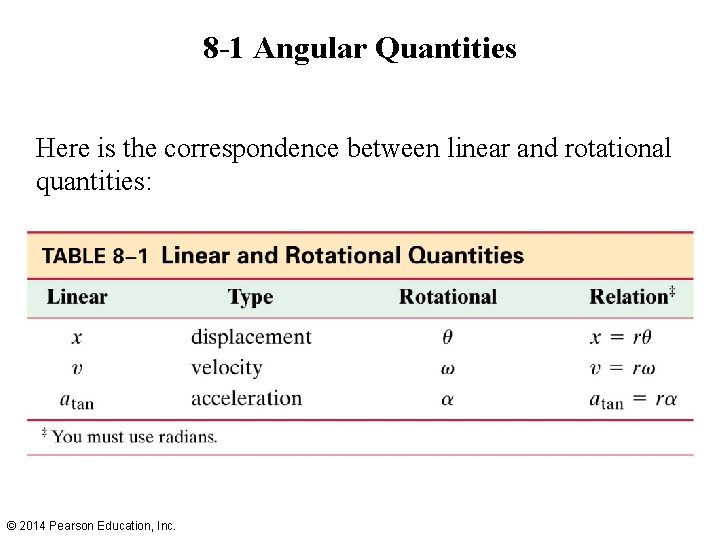
8 -1 Angular Quantities Here is the correspondence between linear and rotational quantities: © 2014 Pearson Education, Inc.

Example 8 -4 A carousel is initially at rest. At t=0 it is given a constant angular acceleration α=0. 060 rad/s 2, which increases its angular velocity for 8. 0 s. At t=8. 0 s, determine a) the angular velocity of the carousel. Given: α=0. 060 rad/s 2, t=8. 0 s Formula: α = Δω Δt Substitution: 0. 060 rad/s 2 = Δω 8. 0 s Answer w/unit: 0. 480 rad/s

Example 8 -4 continues A carousel is initially at rest. At t=0 it is given a constant angular acceleration α=0. 060 rad/s 2, which increases its angular velocity for 8. 0 s. At t=8. 0 s, determine b) the linear velocity of a child coated 2. 5 m from the center, point P. Given: r=2. 5 m, ω=0. 48 rad/s Formula: v = rω Substitution: v= (2. 5 m) (0. 48 rad/s) Answer w/unit: 1. 20 m/s

Example 8 -5 For the child on the rotating carousel of Example 8 -4, determine that child’s Given: r=2. 5 m, ω=0. 48 rad/s, α=0. 060 rad/s 2, t=8. 0 s, v=1. 2 m/s a) tangential (linear) acceleration. Formula: atan = rα Substitution: atan=(2. 5 m)(0. 060 rad/s 2) Answer w/unit: 0. 150 m/s 2 b) Centripetal acceleration. Formula: ac=v 2/r Substitution: ac=(1. 2 m/s)2/2. 5 m Answer w/unit: 0. 576 m/s 2

Example 8 -5 continues For the child on the rotating carousel of Example 8 -4, determine that child’s Given: r=2. 5 m, ω=0. 48 rad/s, α=0. 060 rad/s 2, t=8. 0 s, v=1. 2 m/s c) Total acceleration. Formula: atotal = atan + arot Approach: To find the total, I need to use the Pythagorean theorem. Using the diagram, I see that the atotal is the hypothenuse, and the atan and arot represent the sides. This is just like solving for vectors. Substitution: atotal 2=(0. 150 m/s 2)2+(0. 576 m/s 2)2 Answer w/unit: 0. 600 m/s 2 Tan-1 0. 150 m/s 2 = 0. 25 rad 0. 576 m/s 2 0. 600 m/s 2 at 0. 25 rad

8 -1 Angular Quantities The frequency is the number of complete revolutions per second: f = ω/2π Frequencies are measured in hertz. 1 Hz = 1 s− 1 The period is the time one revolution takes: (8 -8) © 2014 Pearson Education, Inc.

Example In example 8 -4 we found that the carousel, after 8. 0 s, rotates at an angular velocity ω=0. 48 rad/s, and continues to do so after t=8. 0 s because the acceleration ceased. What are the frequency and period of the carousel when rotating at this constant angular velocity ω=0. 48 rad/s? Given: ω=0. 48 rad/s, t=8. 0 s Formula: f = ω 2π Substitution: f = 0. 48 rad/s 2π Answer w/unit: 0. 0764 Hz Next, find period. Formula: T = 1/f Substitution: T = ___1___ 0. 0764 Hz Answer w/unit: 13. 1 s

8 -2 Constant Angular Acceleration The equations of motion for constant angular acceleration are the same as those for linear motion, with the substitution of the angular quantities for the linear ones. © 2014 Pearson Education, Inc.

Example 8 -6 A centrifuge rotor is accelerated for 30 s from rest to 20, 000 rpm (revolutions per minute). a) What is the average angular acceleration? Given: f=20, 000 rpm=333 Hz, t=30 s, ωo=0 rad/s Approach: To determine α=Δω/Δt, we need the initial and final angular velocities. Solve for final angular velocity by using f = ω 2π Formula: f = ω 2π Substitution: 333 Hz= ω 2π Answer w/unit: 2094 rad/s Next, find α. Formula: α=Δω/Δt Substitution: α = _2094 rad/s-0 rad/s_ 30 s Answer w/unit: 69. 8 rad/s 2

Example 8 -6 continues A centrifuge rotor is accelerated for 30 s from rest to 20, 000 rpm (revolutions per minute). b) Through how may revolutions has the centrifuge rotor turned during its acceleration period, assuming constant angular acceleration? Given: t=30 s, α=69. 8 rad/s 2 Approach: Since one revolution corresponds to Ɵ=2πrad, I can use one of the constant acceleration formulas to solve for Ɵ, then convert to revs. Formula: Ɵ = ω0 t + ½αt 2 Substitution: Ɵ = (0 rad/s)(30 s) + ½(69. 8 rad/s 2)(30 s)2 Answer w/unit: 3. 14 x 104 rad Convert to revs. Substitution: 3. 14 x 104 rad x 1 rev 2πrad Answer w/unit: 5000 revs

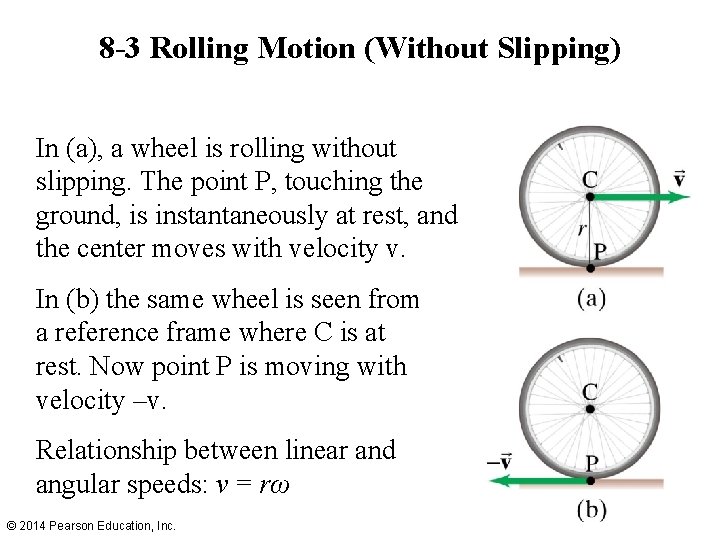
8 -3 Rolling Motion (Without Slipping) In (a), a wheel is rolling without slipping. The point P, touching the ground, is instantaneously at rest, and the center moves with velocity v. In (b) the same wheel is seen from a reference frame where C is at rest. Now point P is moving with velocity –v. Relationship between linear and angular speeds: v = rω © 2014 Pearson Education, Inc.

Example 8 -7 A bicycle slows down uniformly from v 0 =8. 40 m/s to rest over a distance of 115 m. Each wheel and tire has an overall diameter of 68. 0 cm. Determine Given: v 0 =8. 40 m/s, vf=0 m/s, d=115 m, diameter=68. 0 cm=0. 68 m Approach: We will assume that the bicycle wheels roll without slipping and the tire is in firm contact with the ground. The speed of the bike v and the angular velocity ω of the wheels are related by v=rω. The bike slows down uniformly, so the angular acceleration is constant. a) The angular velocity of the wheels at the initial instant (t=0). Approach: Use diameter to determine radius using equation diameter=2 r to get a radius of 0. 34 m. Formula: v 0 = rω0 Substitution: 8. 40 m/s = (0. 34 m)ω0 Answer w/unit: 24. 7 rad/s

Example 8 -7 continues A bicycle slows down uniformly from v 0 =8. 40 m/s to rest over a distance of 115 m. Each wheel and tire has an overall diameter of 68. 0 cm. Determine Given: v 0 =8. 40 m/s, vf=0 m/s, d=115 m, diameter=68. 0 cm=0. 68 m Approach: We will assume that the bicycle wheels roll without slipping and the tire is in firm contact with the ground. The speed of the bike v and the angular velocity ω of the wheels are related by v=rω. The bike slows down uniformly, so the angular acceleration is constant. b) The total number of revolutions each wheel rotates before coming to rest. Approach: In coming to a stop, the bike passes over 115 m of ground. The circumference of the wheel is 2πr. Using that knowledge will allow you to solve for revs. Substitution: revs = 115 m x 1 rev 2πr Answer w/unit: 53. 8 revs

Example 8 -7 continues A bicycle slows down uniformly from v 0 =8. 40 m/s to rest over a distance of 115 m. Each wheel and tire has an overall diameter of 68. 0 cm. Determine Given: v 0 =8. 40 m/s, v=0 m/s, d=115 m, diameter=68. 0 cm=0. 68 m, revolutions=53. 8 revs, ω0=24. 7 rad/s, ω=0 rad/s Approach: We will assume that the bicycle wheels roll without slipping and the tire is in firm contact with the ground. The speed of the bike v and the angular velocity ω of the wheels are related by v=rω. The bike slows down uniformly, so the angular acceleration is constant. c) The angular acceleration of the wheel. Approach: Find angular acceleration by using one of the constant acceleration equations. Ɵ can be found using the relationship that 1 rev corresponds to 2πradians of angle. Formula: ω2 = ωo 2 + 2αƟ Substitution: 0 rad/s = (24. 7 rad/s)2 + 2 α(2πradians/revs x 53. 8 revs) Answer w/unit: -0. 904 rad/s 2

Example 8 -7 continues A bicycle slows down uniformly from v 0 =8. 40 m/s to rest over a distance of 115 m. Each wheel and tire has an overall diameter of 68. 0 cm. Determine Given: v 0 =8. 40 m/s, v=0 m/s, d=115 m, diameter=68. 0 cm=0. 68 m, revolutions=53. 8 revs, ω0=24. 7 rad/s, ω=0 rad/s, α=-0. 904 rad/s 2 Approach: We will assume that the bicycle wheels roll without slipping and the tire is in firm contact with the ground. The speed of the bike v and the angular velocity ω of the wheels are related by v=rω. The bike slows down uniformly, so the angular acceleration is constant. d) The time it took to come to a stop. Formula: ω = ωo + αt Substitution: 0 rad/s = (24. 7 rad/s)2 + (-0. 904 rad/s 2)t Answer w/unit: 27. 3 s

8 -4 Torque To make an object start rotating, a force is needed; the position and direction of the force matter as well. The perpendicular distance from the axis of rotation to the line along which the force acts is called the lever arm. © 2014 Pearson Education, Inc.

8 -4 Torque A longer lever arm is very helpful in rotating objects. © 2014 Pearson Education, Inc.

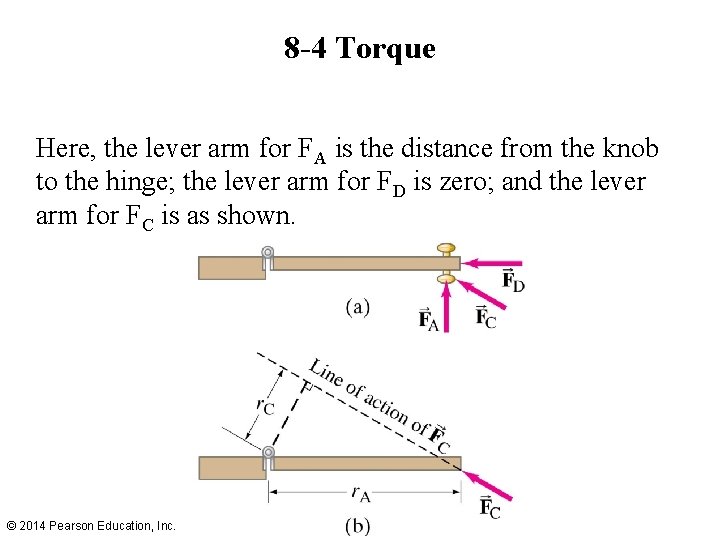
8 -4 Torque Here, the lever arm for FA is the distance from the knob to the hinge; the lever arm for FD is zero; and the lever arm for FC is as shown. © 2014 Pearson Education, Inc.

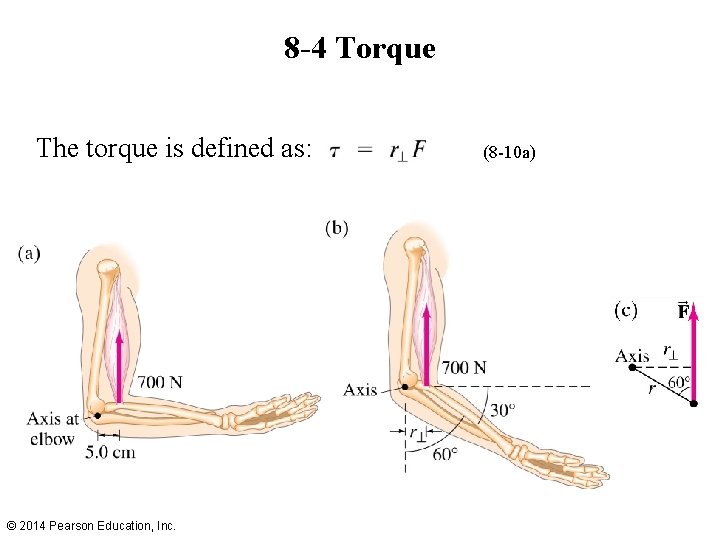
8 -4 Torque The torque is defined as: © 2014 Pearson Education, Inc. (8 -10 a)

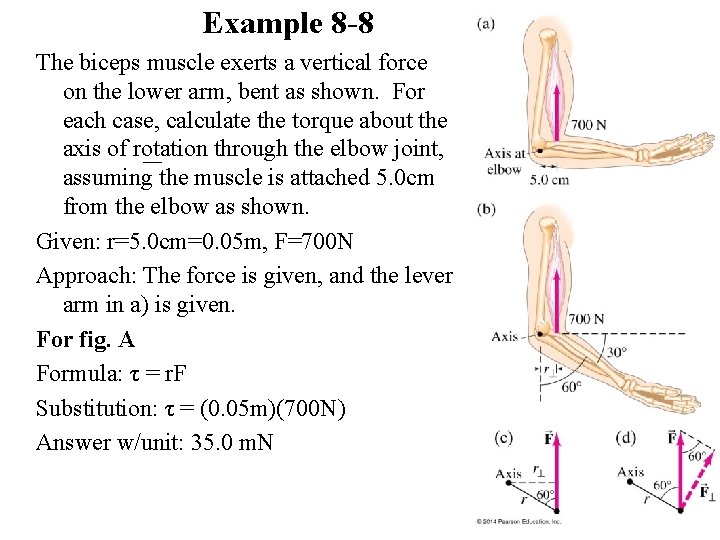
Example 8 -8 The biceps muscle exerts a vertical force on the lower arm, bent as shown. For each case, calculate the torque about the axis of rotation through the elbow joint, assuming the muscle is attached 5. 0 cm from the elbow as shown. Given: r=5. 0 cm=0. 05 m, F=700 N Approach: The force is given, and the lever arm in a) is given. For fig. A Formula: τ = r. F Substitution: τ = (0. 05 m)(700 N) Answer w/unit: 35. 0 m. N

Example 8 -8 continues The biceps muscle exerts a vertical force on the lower arm, bent as shown. For each case, calculate the torque about the axis of rotation through the elbow joint, assuming the muscle is attached 5. 0 cm from the elbow as shown. Given: r=5. 0 cm=0. 05 m, F=700 N Approach: The force is given, and for the lever arm in b) we have to take into account the angle to get the lever arm. Because the arm is at an angle below the horizontal, the lever arm is shorter than in part a. For fig. B Formula: τ = r cosƟF Substitution: τ = (0. 05 m)(cos 30º)(700 N) Answer w/unit: 30. 0 m. N

Example Two forces (FA =20 N and FB =30 N) are applied to a meterstick which can rotate about its left end. Force FB is applied perpendicularly at the midpoint. Which force exerts the greater torque: FA, FB, or both the same? The one with the greater arm will exert a greater torque so FA is the answer.

8 -5 Rotational Dynamics; Torque and Rotational Inertia Knowing that F = ma, we see that τ = mr 2α This is for a single point mass; what about an extended object? As the angular acceleration is the same for the whole object, we can write: (8 -12) © 2014 Pearson Education, Inc.

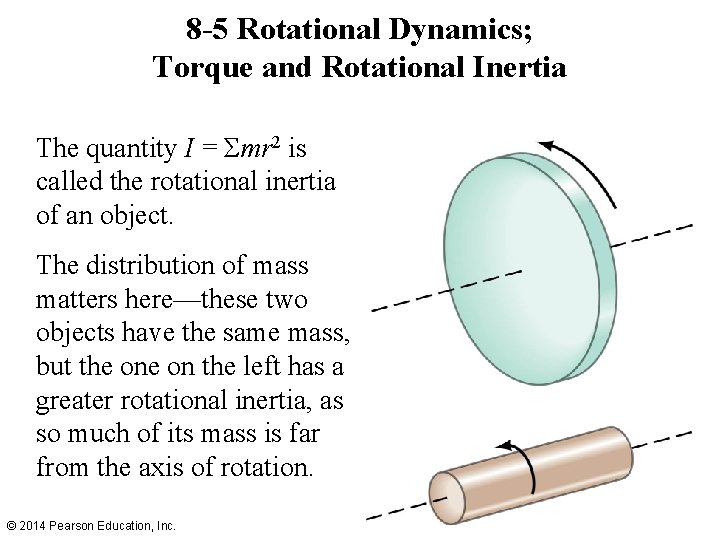
8 -5 Rotational Dynamics; Torque and Rotational Inertia The quantity I = Σmr 2 is called the rotational inertia of an object. The distribution of mass matters here—these two objects have the same mass, but the on the left has a greater rotational inertia, as so much of its mass is far from the axis of rotation. © 2014 Pearson Education, Inc.

Example 8 -9 Two small “weights, ” of mass 5. 0 kg and 7. 0 kg, are mounted 4. 0 m apart on a light rod (whose mass can be ignored), as shown in figure. Calculate the moment of inertia of the system a) when rotated about an axis halfway between the weights a), and b) when rotated about an axis 0. 50 m to the left of the 5. 0 kg mass(b). Given: m 1=5. 0 kg, m 2=7. 0 kg Approach: In each case, the moment of inertia of the system is found by summing over the two parts. For part a. Formula: I=∑mr 2 Substitution: I=(5. 0 kg)(2. 0 m)2 + (7. 0 kg)(2. 0 m)2 Answer w/unit: 48. 0 kgm 2 For part b. Formula: I=∑mr 2 Substitution: I=(5. 0 kg)(0. 5 m)2 + (7. 0 kg)(4. 5 m)2 Answer w/unit: 143 kgm 2

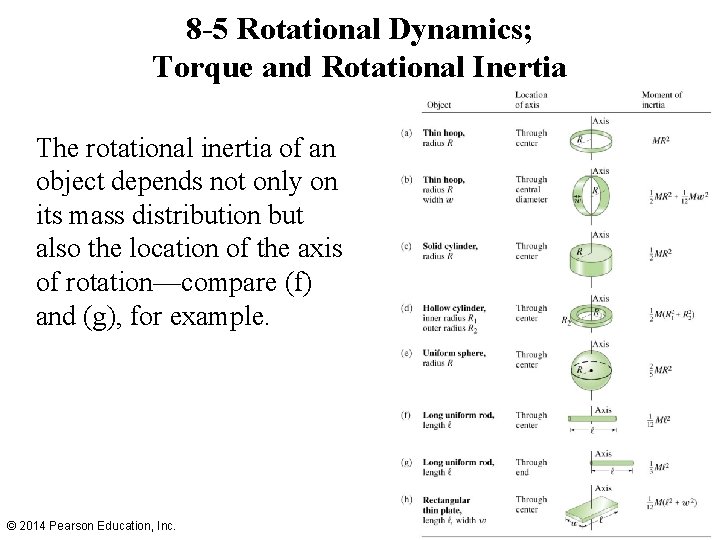
8 -5 Rotational Dynamics; Torque and Rotational Inertia The rotational inertia of an object depends not only on its mass distribution but also the location of the axis of rotation—compare (f) and (g), for example. © 2014 Pearson Education, Inc.

8 -6 Solving Problems in Rotational Dynamics 1. Draw a diagram. 2. Decide what the system comprises. 3. Draw a free-body diagram for each object under consideration, including all the forces acting on it and where they act. 4. Find the axis of rotation; calculate the torques around it. 5. Apply Newton’s second law for rotation. If the rotational inertia is not provided, you need to find it before proceeding with this step. 6. Apply Newton’s second law for translation and other laws and principles as needed. 7. Solve. 8. Check your answer for units and correct order of magnitude. © 2014 Pearson Education, Inc.

Example 8 -10 A 15. 0 N force (represented by FT ) is applied to a cord wrapped around a pulley of mass M=4. 00 kg and radius R=33. 0 cm. The pulley accelerates uniformly from rest to an angular speed of 30. 0 rad/s in 3. 00 s. If there is a frictional torque τfr =1. 10 m. N at the axle, determine the moment of inertia of the pulley. The pulley rotates about its center. Approach: Go through problem solving steps. Here I will start at step 5(apply Newton’s 2 nd law). Step 5: Before I can apply Newton’s 2 nd law (I=∑τ/α), I will have to find the net torque then angular acceleration ∑τ=RFT – τfr = (0. 33 m)(15. 0 N) – 1. 10 m. N=3. 85 m. N α=Δω/Δt=(30. 0 rad/s)/(3. 00 s)=10. 0 rad/s 2

Example 8 -10 continues A 15. 0 N force (represented by FT ) is applied to a cord wrapped around a pulley of mass M=4. 00 kg and radius R=33. 0 cm. The pulley accelerates uniformly from rest to an angular speed of 30. 0 rad/s in 3. 00 s. If there is a frictional torque τfr =1. 10 m. N at the axle, determine the moment of inertia of the pulley. The pulley rotates about its center. Approach: Go through problem solving steps. Here I will start at step 5(apply Newton’s 2 nd law). Step 6: No other calculations needed Step 7: Solve for unknown: moment of inertia I=∑τ/α=(3. 85 m. N)/10. 0 rad/s 2=0. 385 kgm 2 Step 8: You can check your answer to make sure you solved correctly.

Example 8 -11 Consider again the pulley in Ex. 8 -10. But instead of a constant 15. 0 N force being exerted on the Cord, we now have a bucket of Weight w=15. 0 N (mass m=w/g=1. 53 kg) hanging from the cord. We assume the cord has negligible mass and does not stretch or slip on the pulley. Calculate the angular acceleration α of the pulley and the linear acceleration a of the bucket. Assume the same frictional torque τfr=1. 10 m. N acts. Approach: The situation looks a lot like ex. 8 -10. But there is a big difference: the tension in the cord is now an unknown, and it is n o longer equal to the weight of the bucket if the bucket accelerates. Our system has two parts: the bucket, whhich can undergo translational motion; and the pulley. The pulley does not translate, but it can rotate. We apply the rotational version of Newton’s 2 nd law to the pulley, I=∑τ/α, and the linear version to the bucket, ∑F=ma.

Example 8 -11 continues • • • Apply Newton’s 2 nd law(I=∑τ/α) to the pulley and we get Iα=∑τ=RFT-τfr Apply Newton’s 2 nd law (∑F=ma) to the bucket and we get mg. FT=ma. To obtain α, use the fact that the tangential acceleration of a point on the edge of the pulley is the same as the acceleration of the bucket if the cord doesn’t stretch or slip. So I can use atan=a=Rα. Substituting this equation into the equation for the bucket, I get mg-FT=m. Rα. To create one equation to solve, substitute the new bucket equation(rearrange equation to solve for FT first) into the pulley equation to get Iα=∑τ=RFT-τfr=R(mg-m. Rα) –τfr=mg. R-m. R 2α-τfr You can rearrange the equation to solve for α or you can substitute given into equation as written.

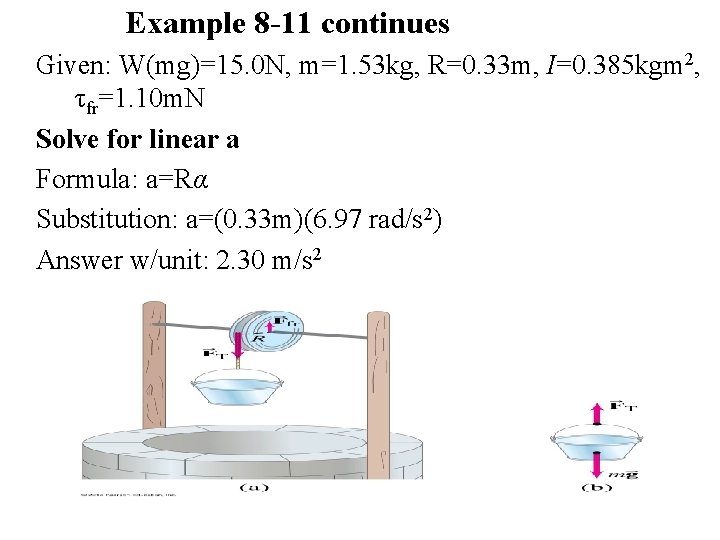
Example 8 -11 continues Given: W(mg)=15. 0 N, m=1. 53 kg, R=0. 33 m, I=0. 385 kgm 2, τfr=1. 10 m. N Rearranging the equation to solve for α Formula: Iα= mg. R- m. R 2α-τfr Iα + m. R 2α =mg. R –τfr α(I+ m. R 2)=mg. R –τfr α= mg. R –τfr I+ m. R 2 Substitution: α= mg. R –τfr = (15. 0 N)(0. 33 m)-1. 10 m. N I+ m. R 2 0. 385 kgm 2 + (1. 53 kg)(0. 33 m)2 Answer w/unit: 6. 97 rad/s 2

Example 8 -11 continues Given: W(mg)=15. 0 N, m=1. 53 kg, R=0. 33 m, I=0. 385 kgm 2, τfr=1. 10 m. N Solve for linear a Formula: a=Rα Substitution: a=(0. 33 m)(6. 97 rad/s 2) Answer w/unit: 2. 30 m/s 2

8 -7 Rotational Kinetic Energy The kinetic energy of a rotating object is given by KE = Σ(½ mv 2) By substituting the rotational quantities, we find that the rotational kinetic energy can be written: (8 -15) A object that has both translational and rotational motion also has both translational and rotational kinetic energy: (8 -16) © 2014 Pearson Education, Inc.

Example 8 -12 What will be the speed of a solid sphere of mass M and radius R when it reaches the bottom of an incline if it starts from rest at a vertical height H and rolls without slipping? (Assume sufficient static friction so no slipping occurs: we will see shortly that static friction does no work. ) Compare your result to that for an object sliding down a frictionless incline. Approach: We use the law of conservation of energy with gravitational potential energy, now including rotational kinetic energy as well as translational KE. Formula: E= 1/2 Mv 2+1/2 ICMω2+Mgy Etop = Ebottom 1/2 Mv 2+1/2 ICMω2+Mgy= 1/2 Mv 2+1/2 ICMω2+Mgy 0 + Mgy= 1/2 Mv 2+1/2 ICMω2+ 0

Example 8 -12 continues What will be the speed of a solid sphere of mass M and 2 radius R when it reaches the bottom of an incline if it starts from rest at a vertical height H and rolls without slipping? (Assume sufficient static friction so no slipping occurs: we will see shortly that static friction does no work. ) Compare your result to that for an object sliding down a frictionless incline. Approach: Substitute the moment of inertia for a solid sphere (see table) for I and since the sphere rolls without slipping, we substitute ω=v/R for ω. Simplify the resultant equation then solve for v. Formula: Mgy= 1/2 Mv 2+1/2 ICMω2 Mgy= 1/2 Mv 2+1/2(2/5 MR 2)(v 2/R 2) M’s and R’s will cancel (because it’s the same object), we get gy= 1/2 v 2+2/10 v 2 gy= 7/10 v 2 Equation for a rolling sphere √(10/7 gy)=v

Example 8 -12 continues What will be the speed of a solid sphere of mass M and 2 radius R when it reaches the bottom of an incline if it starts from rest at a vertical height H and rolls without slipping? (Assume sufficient static friction so no slipping occurs: we will see shortly that static friction does no work. ) Compare your result to that for an object sliding down a frictionless incline. Approach: Compare the speed of a rolling sphere to that for an object sliding down a plane without rotating and without friction(just translational motion). Rearrange the equation to solve for v. Formula: top = bottom Mgy+1/2 Mv 2= 1/2 Mv 2+Mgy Mgy+ 0 = 1/2 Mv 2+ 0 M’s will cancel (because it’s the same object), we get gy= 1/2 v 2 Equation for a sliding sphere gy= 7/10 v 2 √(2 gy)=v Since the sliding object transforms its initial PE entirely into translational KE, the speed of its center of mass is greater.

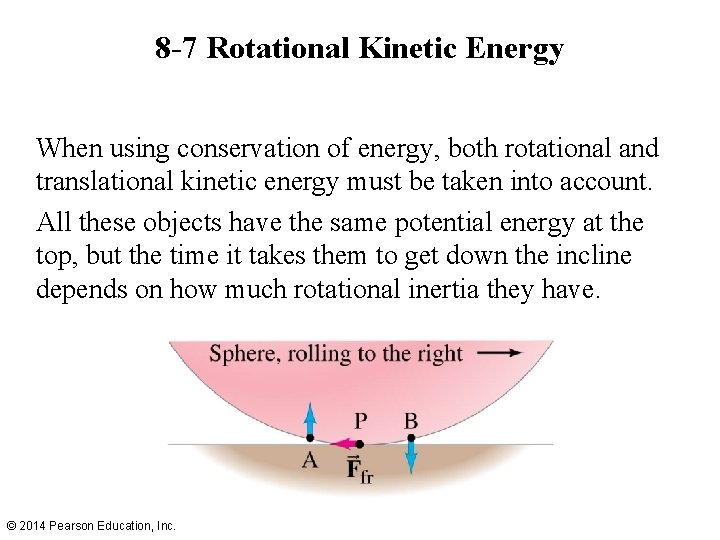
8 -7 Rotational Kinetic Energy When using conservation of energy, both rotational and translational kinetic energy must be taken into account. All these objects have the same potential energy at the top, but the time it takes them to get down the incline depends on how much rotational inertia they have. © 2014 Pearson Education, Inc.

Example 8 -13 Several objects roll without slipping down an incline of vertical height H, all starting from rest at the same moment. The objects are a thin hoop (or a plain wedding band), a spherical marble, a solid cylinder (a D-cell battery), and an empty soup can. In addition, a greased box slides down without friction. In what order do they reach the bottom of the incline? Answer: We use conservation of energy with gravitational PE plus translational KE. The sliding box would be fastest because the PE loss is transformed completely into translational KE of the box, whereas for rolling objects the initial PE is shared between translational and rotational KE, and so the speed of the CM is less. For each of the rolling objects we can state that the decrease in PE equals the increase in translational plus rotational KE: Mg. H=1/2 mv 2 + 1/2 Icmω2.

Example 8 -13 Several objects roll without slipping down an incline of vertical height H, all starting from rest at the same moment. The objects are a thin hoop (or a plain wedding band), a spherical marble, a solid cylinder (a D-cell battery), and an empty soup can. In addition, a greased box slides down without friction. In what order do they reach the bottom of the incline? Answer: For all rolling objects, the moment of inertia I is a numerical factor times the mass M and the radius R 2. The mass M is in each term, so the translational speed v doesn’t depend on M; nor does it depend on the radius R since ω=v/R, so R 2 cancels out for all the rolling objects. Thus the speed v at the bottom of the incline depends only on that numerical factor in ICM which expresses how the mass is distributed (use the table to look up the ICM equations). Fastest to slowest Box> sphere> solid cylinder>empty can>hoop

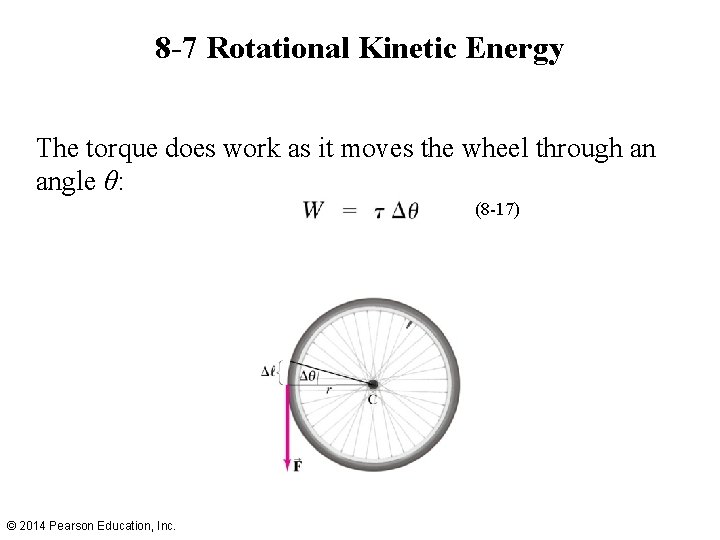
8 -7 Rotational Kinetic Energy The torque does work as it moves the wheel through an angle θ: (8 -17) © 2014 Pearson Education, Inc.

8 -8 Angular Momentum and Its Conservation In analogy with linear momentum, we can define angular momentum L: (8 -18) We can then write the total torque as being the rate of change of angular momentum. If the net torque on an object is zero, the total angular momentum is constant. Iω = I 0ω0 = constant © 2014 Pearson Education, Inc.

8 -8 Angular Momentum and Its Conservation Therefore, systems that can change their rotational inertia through internal forces will also change their rate of rotation: © 2014 Pearson Education, Inc.

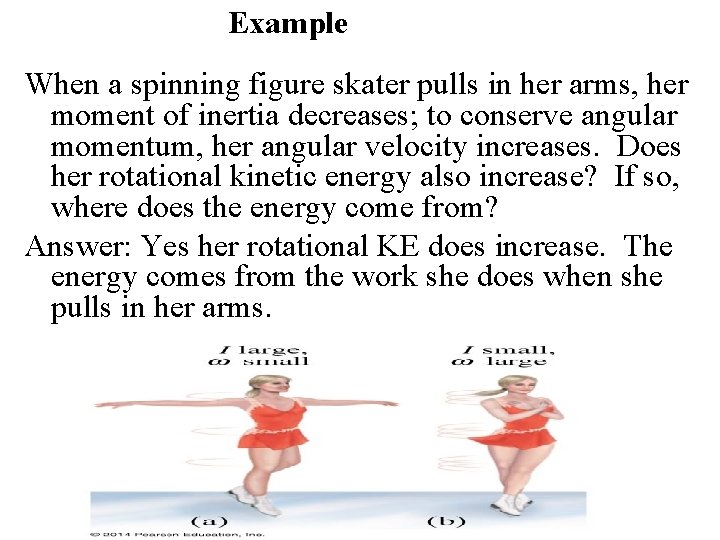
Example When a spinning figure skater pulls in her arms, her moment of inertia decreases; to conserve angular momentum, her angular velocity increases. Does her rotational kinetic energy also increase? If so, where does the energy come from? Answer: Yes her rotational KE does increase. The energy comes from the work she does when she pulls in her arms.

Example 8 -14 A simple clutch consists of two cylindrical plates that can be pressed together to connect two sections of an axle, as needed, in a piece of machinery. The two plates have masses MA=6. 0 kg and MB=9. 0 kg, with equal radii R=0. 60 m. They are initially separated. Plate MA is accelerated from rest to an angular velocity ω1=7. 2 rad/s in time Δt=2. 0 s. Calculate Approach: We use angular momentum, L=Iω, plus Newton’s second law for rotation, ∑τ=ΔL/Δt. For I, use the moment of inertia for a cylinder. Given: MA=6. 0 kg, MB=9. 0 kg, R=0. 60 m, ω1=7. 2 rad/s, Δt=2. 0 s a) the angular momentum of MA Formula: L=Iω1; Substitute cylinder eqn. I=1/2 MAR 2 to get L=1/2 MAR 2ω1 Substitution: L=1/2(6. 0 kg)(0. 60 m)2(7. 2 rad/s) Answer w/unit: 7. 78 kgm 2/s

Example 8 -14 A simple clutch consists of two cylindrical plates that can be pressed together to connect two sections of an axle, as needed, in a piece of machinery. The two plates have masses MA=6. 0 kg and MB=9. 0 kg, with equal radii R=0. 60 m. They are initially separated. Plate MA is accelerated from rest to an angular velocity ω1=7. 2 rad/s in time Δt=2. 0 s. Calculate Approach: We use angular momentum, L=Iω, plus Newton’s second law for rotation, ∑τ=ΔL/Δt. For I, use the moment of inertia for a cylinder. Given: MA=6. 0 kg, MB=9. 0 kg, R=0. 60 m, ω1=7. 2 rad/s, Δt=2. 0 s, L= 7. 78 kgm 2/s b) the torque required to accelerate MA from rest to ω1 Formula: ∑τ=ΔL/Δt Substitution: ∑τ=(7. 78 kgm 2/s-0) /(2. 0 s) Answer w/unit: 3. 89 m. N

Example 8 -14 A simple clutch consists of two cylindrical plates that can be pressed together to connect two sections of an axle, as needed, in a piece of machinery. The two plates have masses MA=6. 0 kg and MB=9. 0 kg, with equal radii R=0. 60 m. They are initially separated. Plate MA is accelerated from rest to an angular velocity ω1=7. 2 rad/s in time Δt=2. 0 s. Calculate C) Next, plate MB, initially at rest but free to rotate without friciton, is placed in firm contact with freely rotating plate MA, and the two plates then both rotate at a constant angular velocity ω2, which is considerably less than ω1. Why does this happen, and what is ω2? Approach: Initially, before contact, MA is rotating at constant ω1 (we ignore friction). When plate B comes in contact, why is their joint rotation speed less? You might think in terms of the torque each exerts on the other upon contact. But quantitatively, it’s easier to use conservation of angular momentum, since no external torques are assumed to act. Thus angular momentum before=angular momentum after. For I, use the moment of inertia for a cylinder (I=1/2 MR 2). Given: MA=6. 0 kg, MB=9. 0 kg, R=0. 60 m, ω1=7. 2 rad/s, Δt=2. 0 s, L= 7. 78 kgm 2/s Formula: 1/2 MAR 2ω1 = (1/2 MAR 2 + 1/2 MBR 2)ω2 ; R’s will cancel out Substitution: 1/2*(6. 0 kg)(7. 2 rad/s) = [1/2(6. 0 kg) + ½(9. 0 kg)]ω2 Answer w/unit: 2. 88 rad/s

Example 8 -15 Astronomers detect stars that are rotating extremely rapidly, known as neutron stars. A neutron star is believed to form from the inner core of a larger star that collapsed, under its own gravitation, to a star of very small radius and very high density. Before collapse, suppose the core of such a star is the size of our Sun (R≈7 x 105 km) with mass 2. 0 times as great as the Sun, and is rotating at a frequency of 1. 0 revolution every 100 days. If it were to undergo gravitational collapse to a neutron star of radius 10 km, what would its rotation frequency be? Assume the star is a uniform sphere at all times, and loses no mass. Approach: We assume the star is isolated (no external forces), so we can use conservation of angular momentum for this process. Given: R 1= 7 x 105 km= 7 x 108 m, f 1=1 rev/100 days=1 rev/(8. 64 x 106 s)=1. 16 x 10 -7 Hz, R 2=10 km=10000 m Formula: I 1ω1= I 2ω2 Substitute sphere eqn. (I=2/5 MR 2) for I to get 2/5 M 1 R 2ω1= 2/5 M 2 R 2ω2. M’s and 2/5’s will cancel out to get R 2ω1= R 2ω2 Since frequency and ω has a direct relationship, I can substitute f for ω in the equation to get R 2 f 1= R 2 f 2 Substitution: (7 x 108 m)2 (1. 16 x 10 -7 Hz)= (10000 m)2 f 2 Answer w/unit: 567 Hz

Summary of Chapter 8 • Angles are measured in radians; a whole circle is 2π radians. • Angular velocity is the rate of change of angular position. • Angular acceleration is the rate of change of angular velocity. • The angular velocity and acceleration can be related to the linear velocity and acceleration. © 2014 Pearson Education, Inc.

Summary of Chapter 8 • The frequency is the number of full revolutions per second; the period is the inverse of the frequency. • The equations for rotational motion with constant angular acceleration have the same form as those for linear motion with constant acceleration. • Torque is the product of force and lever arm. • The rotational inertia depends not only on the mass of an object but also on the way its mass is distributed around the axis of rotation. © 2014 Pearson Education, Inc.

Summary of Chapter 8 • The angular acceleration is proportional to the torque and inversely proportional to the rotational inertia. • An object that is rotating has rotational kinetic energy. If it is translating as well, the translational kinetic energy must be added to the rotational to find the total kinetic energy. • Angular momentum is L = Iω • If the net torque on an object is zero, its angular momentum does not change. © 2014 Pearson Education, Inc.