Lecture Objectives Finish with Review Conduction Boundary Conditions

Lecture Objectives: • Finish with Review – Conduction • Boundary Conditions at External Surfaces

Conduction

Conductive heat transfer k - conductivity of material • Steady-state • Unsteady-state TS 1 TS 2 L • Boundary conditions – Dirichlet Tsurface = Tknown – Neumann Tair h

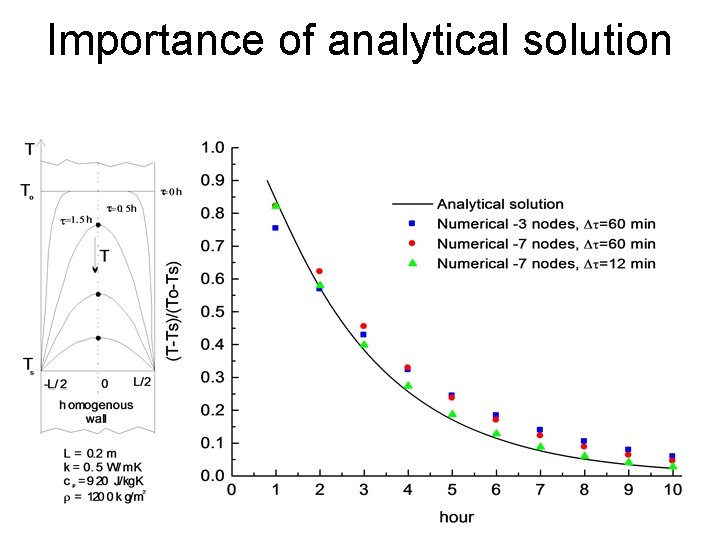
Importance of analytical solution

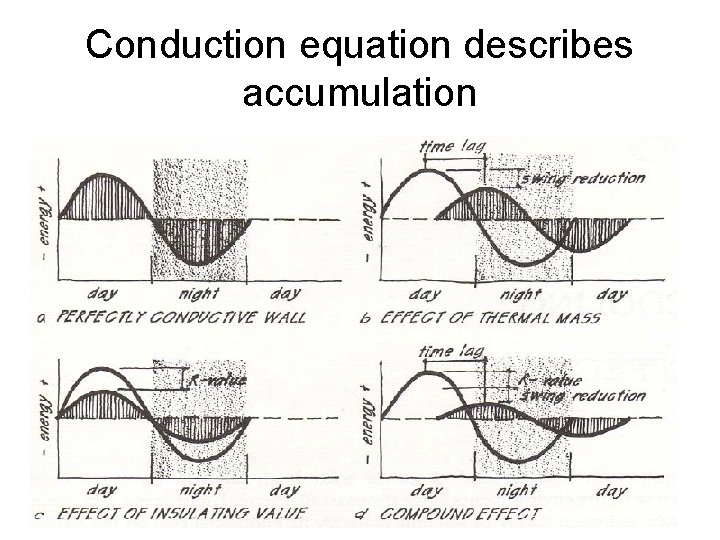
Conduction equation describes accumulation

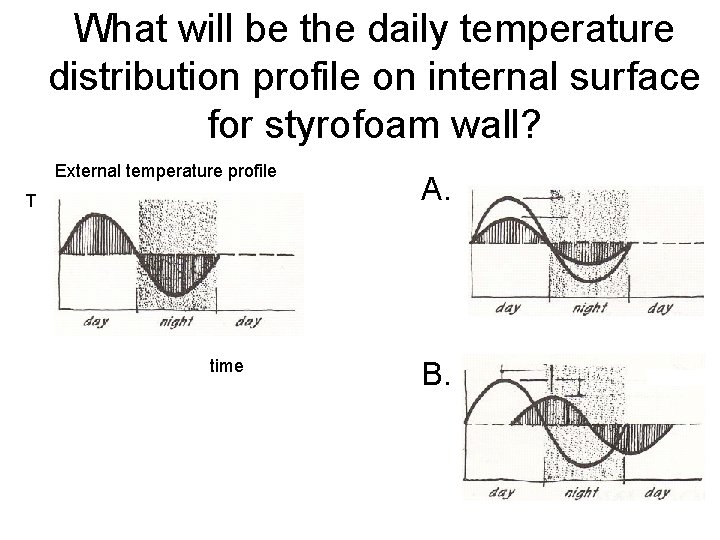
What will be the daily temperature distribution profile on internal surface for styrofoam wall? External temperature profile T time A. B.

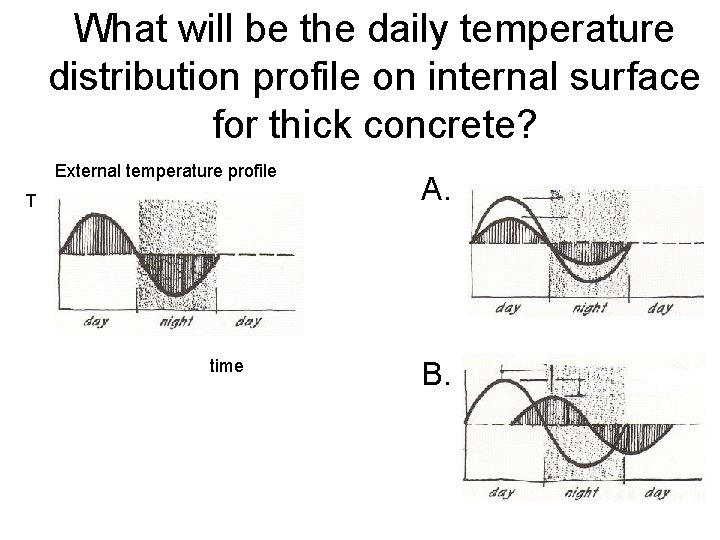
What will be the daily temperature distribution profile on internal surface for thick concrete? External temperature profile T time A. B.

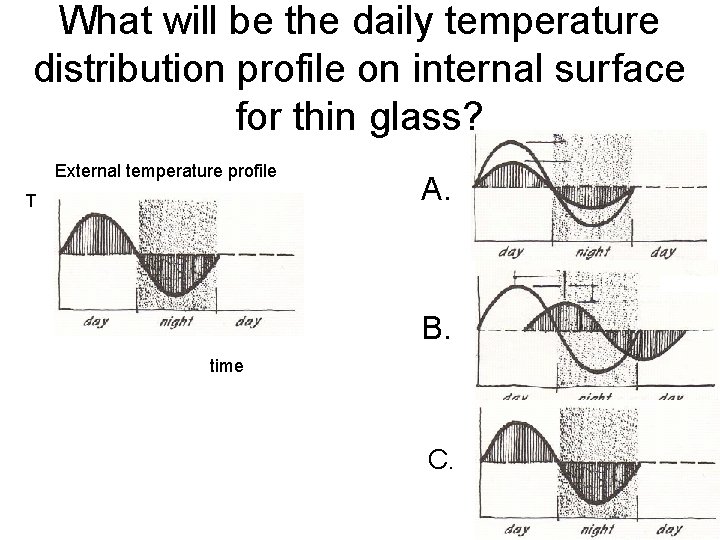
What will be the daily temperature distribution profile on internal surface for thin glass? External temperature profile T A. B. time C.

In buildings conduction is unsteady state We will use numerical solution for this Unsteady-state equation:

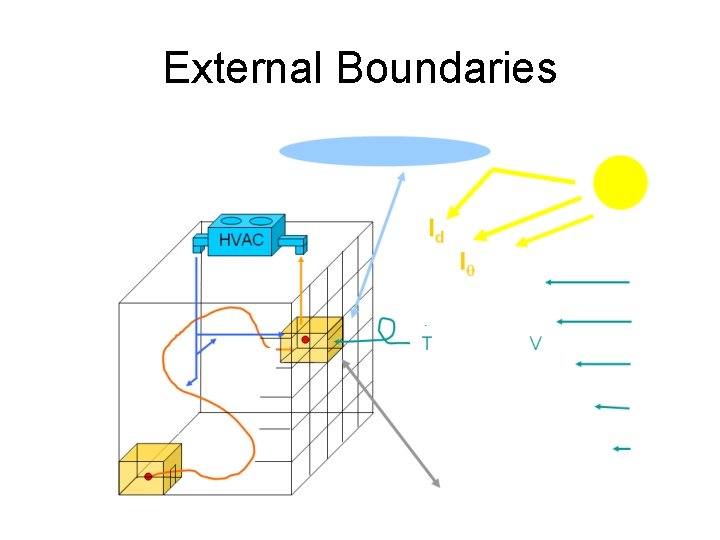
External Boundaries

Radiative heat exchange at external surfaces View (shape) factors for: 1) vertical surfaces: - to sky - to ground 1/2 2) horizontal surfaces: - to sky 1 - to ground 0 3) Tilted surfaces - to sky (1+cosb)/2 - to ground (1 -cosb)/2 General equations: surface b ground

Ground and sky temperatures • Sky temperature • Swinbank (1963, Cole 1976) model -Cloudiness CC [0 -1] 0 – for clear sky , 1 for totally cloud sky -Air temperature Tair [K] Tsky 4 = 9. 365574 · 10− 6(1 − CC) Tair 6+ Tair 4 CC·eclouds Emissivity of clouds: eclouds = (1 − 0. 84·CC)(0. 527 + 0. 161*exp[8. 45·(1 − 273/ Tair)]) + 0. 84 CC For modeled T sky the esky =1 (Modeled T sky is for black body)

Ground and sky temperatures • Sky temperature Berdahl and Martin (1984) model - Cloudiness CC [0 -1] 0 – for clear sky , 1 for totally cloud sky - Air temperature Tair [K] - Dew point temperature Tdp [C] !!! Tclear_sky = Tair (e. Clear 0. 25) e. Clear = 0. 711 + 0. 56(Tdp/100) + 0. 73 (Tdp/100)2 - emissivity of clear sky Ca = 1. 00 +0. 0224*CC + 0. 0035*CC 2 + 0. 00028*CC 3 – effect of cloudiness Tsky = (Ca)0. 25 * Tclear_sky esky =1

Ground and sky temperatures For ground temperature: - We often assume: Tground=Tair -or we calculate Solar-air temperature -Solar-air temperature – imaginary temperature - Combined effect of solar radiation and air temperature Tsolar = f (Tair , Isolar , ground conductivity resistance)

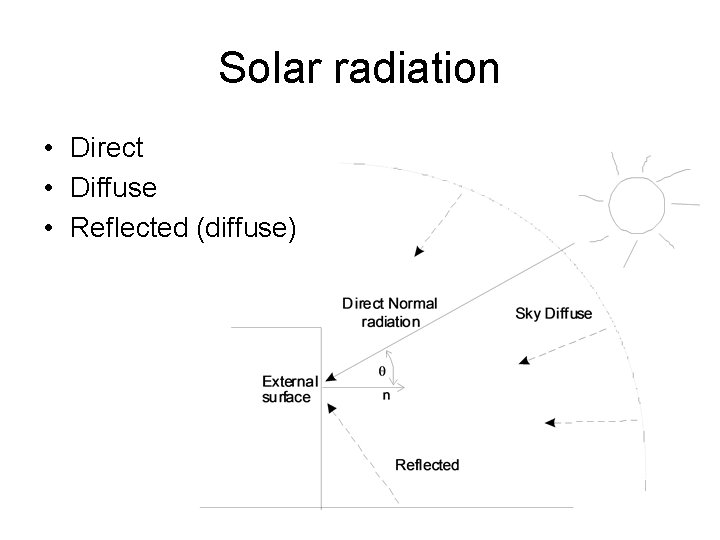
Solar radiation • Direct • Diffuse • Reflected (diffuse)

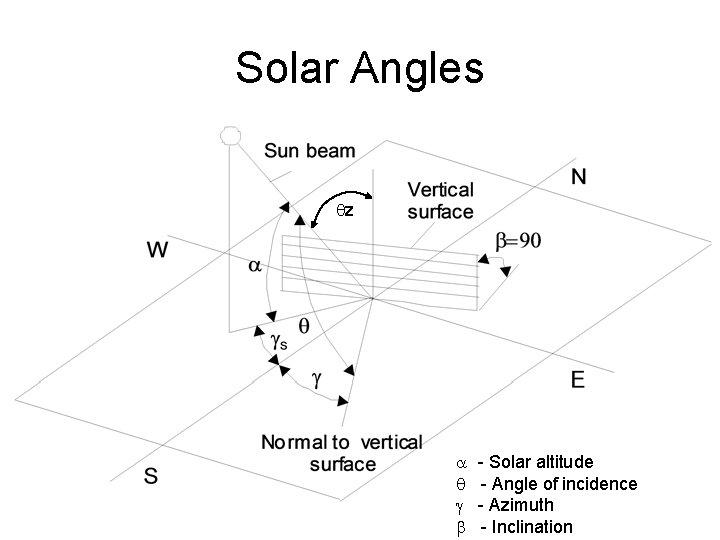
Solar Angles qz a - Solar altitude q - Angle of incidence g - Azimuth b - Inclination

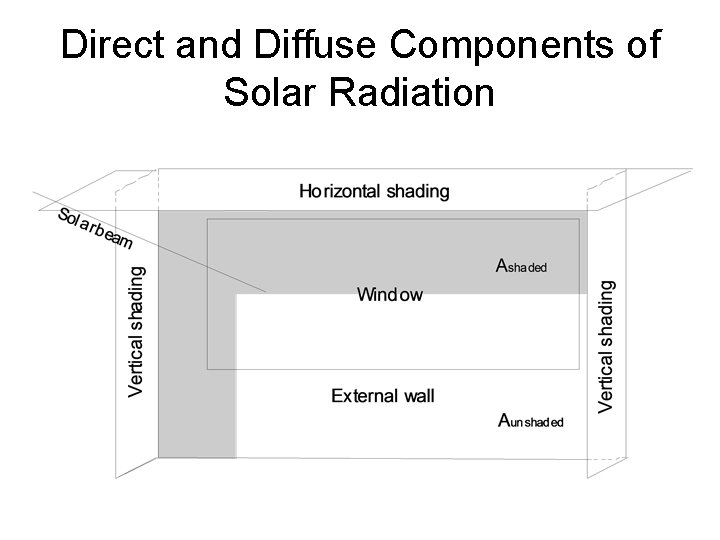
Direct and Diffuse Components of Solar Radiation

Solar components • Global horizontal radiation IGHR • Direct normal radiation IDNR Direct component of solar radiation on considered surface: Diffuse components of solar radiation on considered surface: qz Total diffuse solar radiation on considered surface:

External convective heat flux Presented model is based on experimental data, Ito (1972) Primarily forced convection (wind): Velocity at surfaces that are windward: Velocity at surfaces that are leeward : U -wind velocity Convection coefficient : u surface windward u leeward

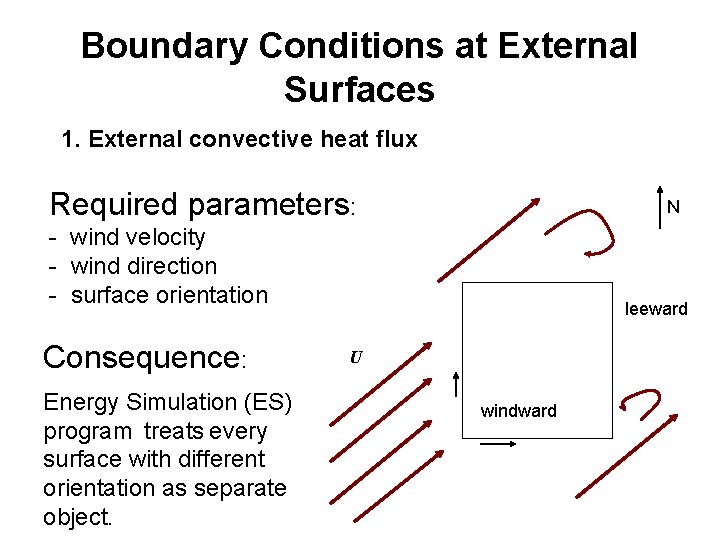
Boundary Conditions at External Surfaces 1. External convective heat flux Required parameters: N - wind velocity - wind direction - surface orientation Consequence: Energy Simulation (ES) program treats every surface with different orientation as separate object. leeward U windward

Wind Direction Wind direction is defined in TMY database: “Value: 0 – 360 o Wind direction in degrees at the hou indicated. ( N = 0 or 360, E = 90, S = 180, W = 270 ). For calm winds, wind direction equals zero. ” N http: //rredc. nrel. gov/solar/old_data/nsrdb/1991 -2005/tmy 3/ http: //rredc. nrel. gov/solar/pubs/tmy 2/tab 3 -2. html leeward U windward Wind direction: ~225 o