Lecture Objectives Boundary Conditions Project 1 software Surface

Lecture Objectives: Boundary Conditions Project 1 (software)

Surface boundaries wall functions Wall surface Introduce velocity temperature and concentration Use wall functions to model the micro-flow in the vicinity of surface Using relatively large mesh (cell) size.

Surface boundaries wall functions Course mesh distribution in the vicinity of surface Y Wall surface Velocity in the first cell will depend on the distance y.

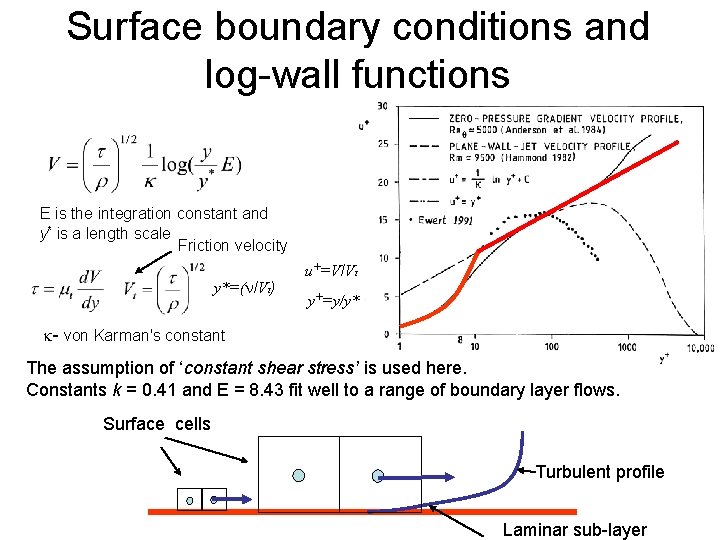
Surface boundary conditions and log-wall functions E is the integration constant and y* is a length scale Friction velocity y*=(n/Vt) u+=V/Vt y+=y/y* k- von Karman's constant The assumption of ‘constant shear stress’ is used here. Constants k = 0. 41 and E = 8. 43 fit well to a range of boundary layer flows. Surface cells Turbulent profile Laminar sub-layer

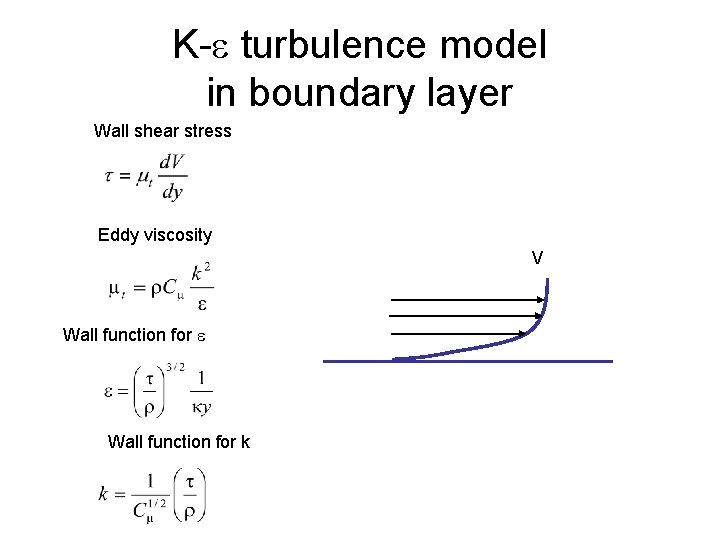
K-e turbulence model in boundary layer Wall shear stress Eddy viscosity V Wall function for e Wall function for k

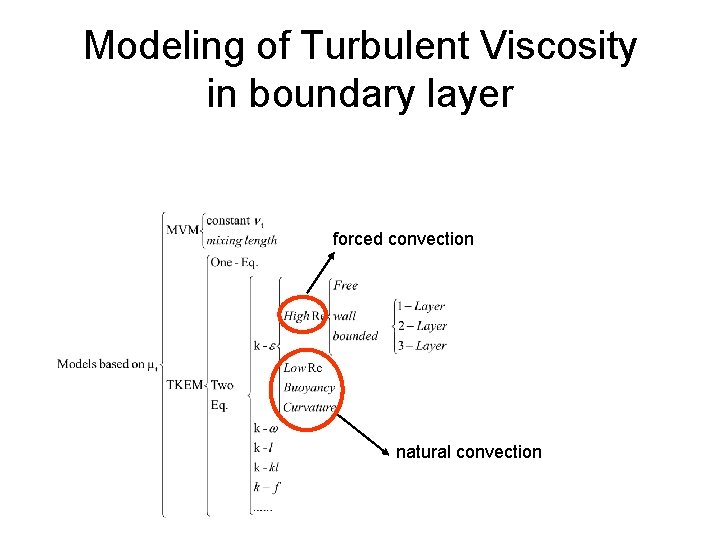
Modeling of Turbulent Viscosity in boundary layer forced convection natural convection

Temperature and concentration gradient in boundary layer Depend on velocity field • Temperature q=h(Ts-Tair) Tair h = f(V) = f(k, e) Ts Into source term of energy equation • Concentration F=hc(Cs-Cair/m) m=Dair/Ds m- segregation coefficient Cair Cs h. C = f(V, material prop. )

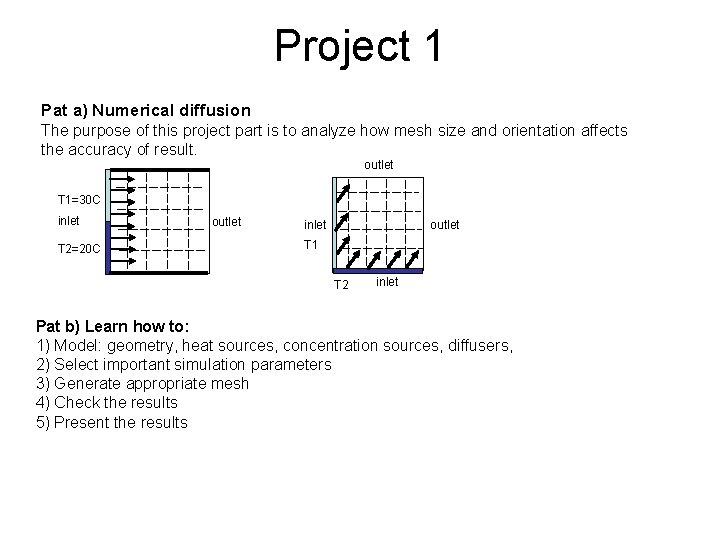
Project 1 Pat a) Numerical diffusion The purpose of this project part is to analyze how mesh size and orientation affects the accuracy of result. outlet T 1=30 C inlet T 2=20 C outlet inlet outlet T 1 T 2 inlet Pat b) Learn how to: 1) Model: geometry, heat sources, concentration sources, diffusers, 2) Select important simulation parameters 3) Generate appropriate mesh 4) Check the results 5) Present the results

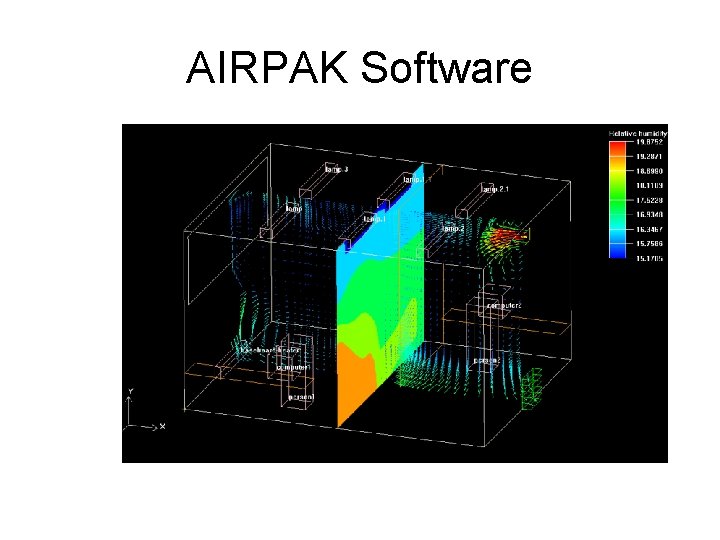
AIRPAK Software

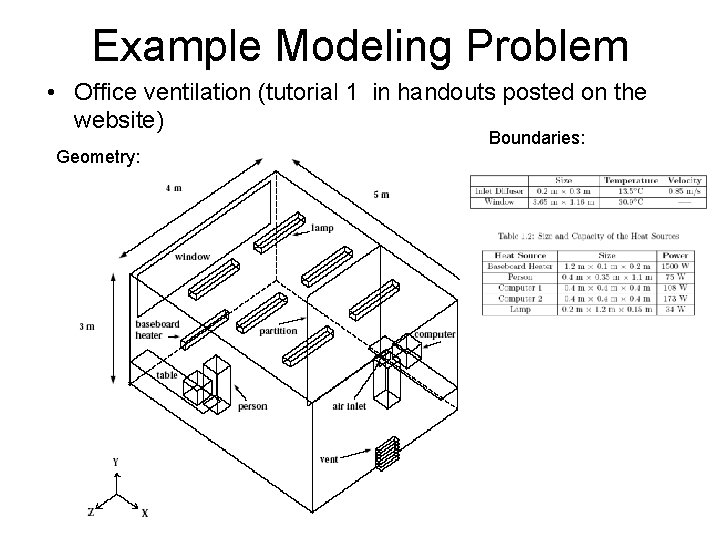
Example Modeling Problem • Office ventilation (tutorial 1 in handouts posted on the website) Geometry: Boundaries:

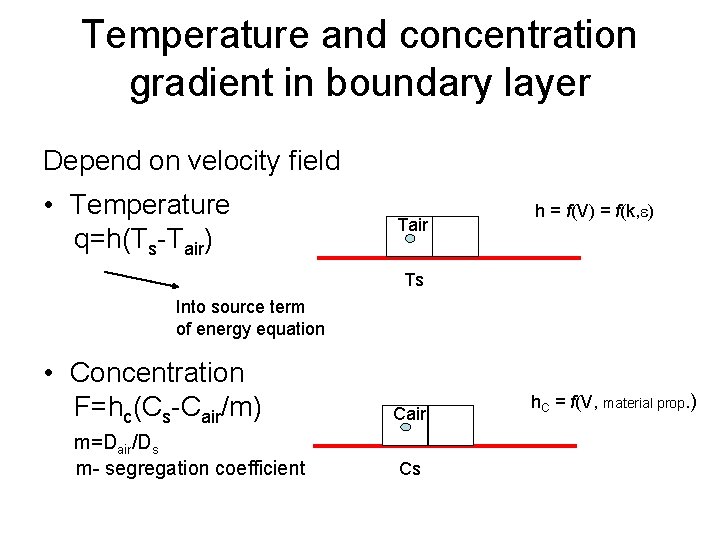
Temperature and concentration gradient in boundary layer Depend on velocity field • Temperature q=h(Ts-Tair) Tair h = f(V) = f(k, e) Ts Into source term of energy equation • Concentration F=hc(Cs-Cair/m) m=Dair/Ds m- segregation coefficient Cair Cs h. C = f(V, material prop. )

Inlets Diffuser Types Valve diffuser swirl diffusers wall or ceiling floor ceiling diffuser

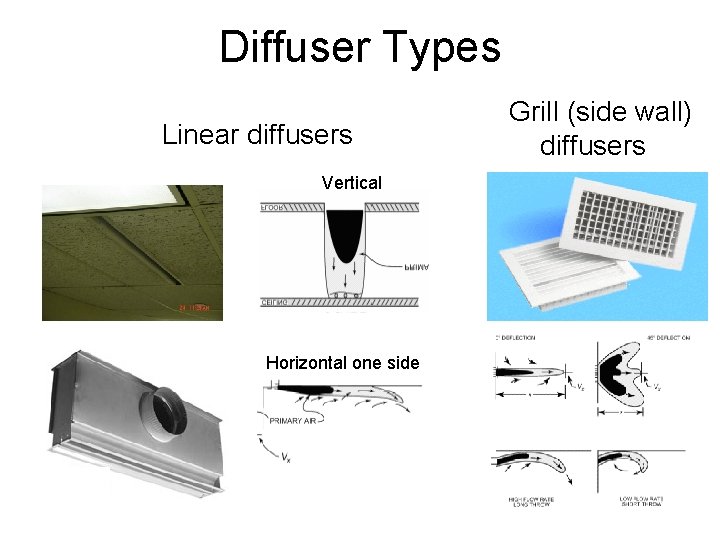
Diffuser Types Linear diffusers Vertical Horizontal one side Grill (side wall) diffusers

Displacement ventilation diffusers

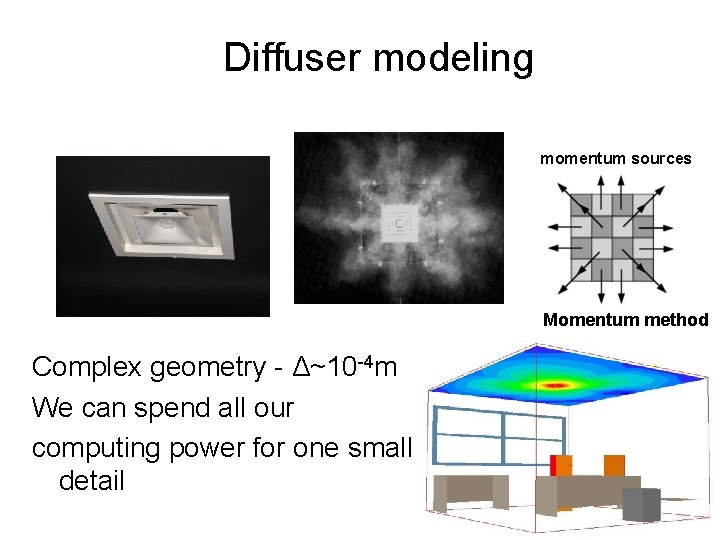
Diffuser modeling momentum sources Momentum method Complex geometry - Δ~10 -4 m We can spend all our computing power for one small detail

Diffuser Modeling Fine mesh or box method for diffuser modeling

Jet parameters A 0 - effective area of the diffuser V 0 – initial jet velocity X - distance from the diffuser Vm – maximum jet velocity at distance x from the diffuser K – property of diffuser

Diffuser properties (ASHRAE)

Project 1 http: //www. costco. com/. product. 100222479. html